一种主轴系统故障识别方法*
赵 川, 王红军, 张怀存
(1.北京信息科技大学 现代测控技术教育部重点实验室,北京 100192; 2.北京信息科技大学 机电工程学院,北京 100192)
一种主轴系统故障识别方法*
赵 川1, 王红军1, 张怀存2
(1.北京信息科技大学 现代测控技术教育部重点实验室,北京 100192; 2.北京信息科技大学 机电工程学院,北京 100192)
故障识别是确定故障类型的重要方式。传统方法不能直观识别故障类型,忽略了水平和垂直方向的信息之间的关系,很难准确提取故障特征。二维全息谱融合了水平和垂直方向的振动信息,反映了一个支承面上转子的振动情况。但在某些情况下不能准确识别主要故障,无法通过分倍频、工频和高倍频的椭圆信息确定故障类型。选择流形学习的LE算法与全息谱技术结合,弥补了二维全息谱算法的缺陷,提高了流形学习处理信号的优越性。通过实验验证了方法的准确性。
二维全息谱;流形学习;主轴系统;故障识别
Abstract: Fault identification is an important way to determine the form of fault. Traditional methods can not intuitively identify fault types, ignoring the relationship between the information of the horizontal and vertical direction and it is difficult to accurately extract the fault feature. Two dimensional holographic spectrum has blend the vibration of horizontal and vertical direction information, reflecting the vibration of the rotor on a supporting surface. But in some cases it can not accurately identify major failure and determine the failure types through elliptic information of points frequency doubling, power frequency and high frequency. Choosing the manifold learning LE algorithm and combined with holographic spectrum technology, making up for the defects of the two dimensional holospectrum algorithm and improving the advantages of manifold learning signal processing. the correct result have been got by experiment.
Key words: two dimensional holographic spectrum; manifold learning; spindle system; fault identification
0 引 言
在主轴系统中,零部件加工和安装方面的缺陷以及机床运行时引起的振动往往是造成机器破坏的主要原因。加工设备发生故障,影响加工精度和质量,并会造成设备的意外停机、缩短工作时间。
为了及时了解设备的技术状态,方便维修,有必要对其重要参数进行监测与研究[1]。故障特征信息是分析诊断的重要内容和基础。运用新的方法对机床主轴系统的微弱信号特征、非线性特征、复合故障特征进行提取与识别,对寻找主轴系统劣化与演变规律有很强的现实意义。
1 全息谱与流行学习原理
1.1 二维全息谱
全息谱技术作为全新的故障分析方法,能把一个支承面的综合信息融合,以全息谱的方式准确表达出来。其中,二维全息谱融合了水平和垂直方向的振动信息,反映了一个支承面上转子的振动情况[2]。
二维全息谱算法将所有频率下复杂的椭圆信息分解到不同频率下,形成更为简单的椭圆,甚至直线或圆的特殊情况。如图1所示,其中横坐标是频率,在横坐标上各频率处为代表相位、幅值关系的椭圆,圆代表相位差90°或270°,直线代表相位差0°或180°。
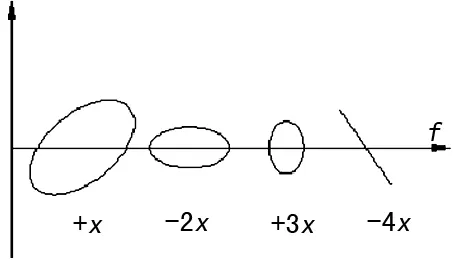
图1 二维全息谱图
长轴表示该频率下最大幅值,短轴表示最小幅值,椭圆离心率表示幅值变化情况,“±”表示转子运动方向。
假设采集某支撑面X和Y方向的信号x(n)和y(n),若对任一振动信号取一段长度为N的样本,加窗并做傅立叶变换,其变换式如下:
(1)
(2)
式中:0≤n≤N-1,0≤k≤N-1,X(k)和Y(k)为复数,改写如式(3)、(4):
Xk=Rk+jIk
(3)
Yk=R2k+jI2k
(4)
则振动信号的幅值谱和相位谱为:
(5)
(6)
αk=tg-1(Ik/Rk)
(7)
βk=tg-1(I2k/R2k)
(8)
设窗函数频谱表达式为f(x),其对应离散频谱为Yx。设f(x-1)、f(x)和f(x+1)为窗函数频谱主瓣内三根相对高的谱线,相对应的其离散频谱中的三根谱线分别为Yx-1、Yx和Yx+1,其中Yx>Yx-1,Yx
(9)
解出x,可得频率校正量Δk=-x。
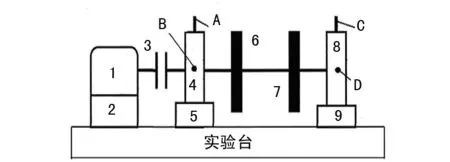
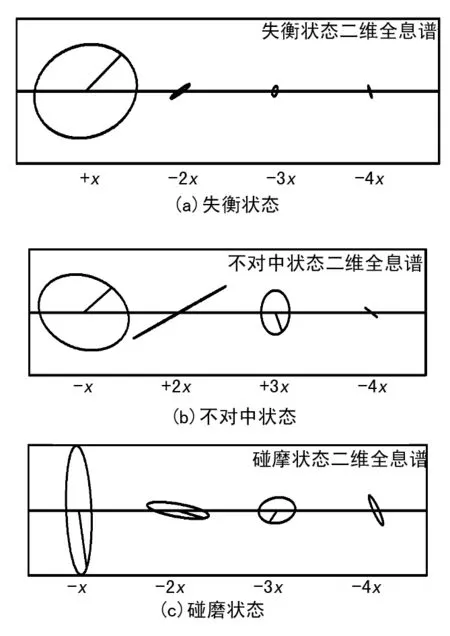
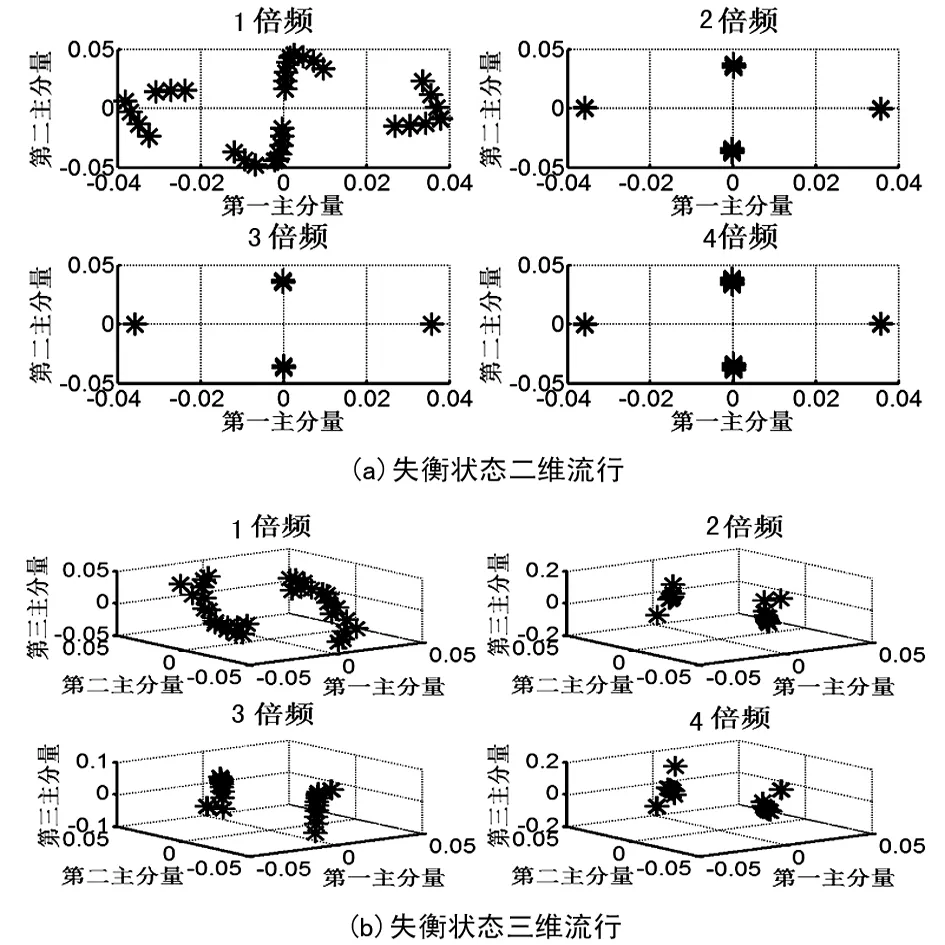
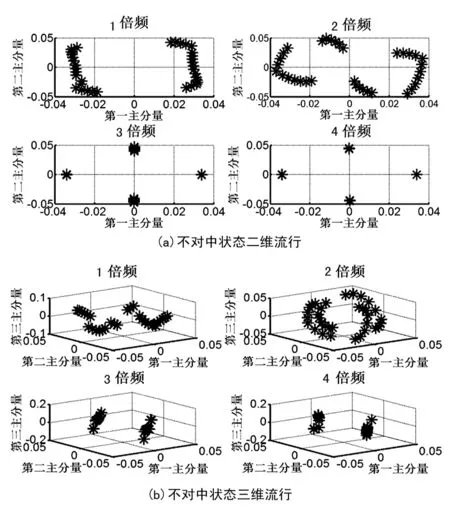
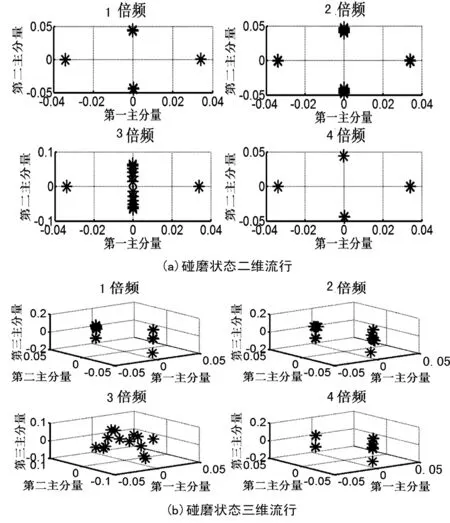
如果Yx+1 (10) 解出x,可得频率校正量Δk=-x-1。 由此,可得校正后的频率为: (11) 式中:k(k=0,1,2,…,N/2-1)表示谱线号,N表示分析点数,fs表示采样频率。 由频率校正量 Δk可得幅值校正量为: (12) (13) 同时,由频率校正量Δk可得相位校正公式为: (14) (15) 式中,因为参数方程的表示方法是正弦函数,相位与相位差在比值校正后存在差异,频域内,两个方向信号的第k根谱线的方程为: x(k)=Ak′sin(kt+αk′) (16) y(k)=Bk′sin(kt+βk′) (17) 消去参数t即可得到经典全息谱方程为: =sin2(βk′-αk′) (18) 由此可得到全息谱中一些重要的结果为: sx=A′cosα′ (19) sy=B′cosβ′ (20) cx=A′sinα′ (21) cy=B′sinβ′ (22) (23) c=A′2+B′2; d=2A′B′sin(α′-β′)。 最后,还能够通过正弦系数SX和SY以及余弦系数CX和CY计算椭圆的起始点、长轴倾角等。 1.2 流形学习及LE算法 1.2.1 流形及流形学习 流形(Manifold)是拓扑学的概念,以微分流形为基础,是几何对象的总称,包括各种曲线和曲面[3]。 流形学习现已成为一种成熟的信号特征提取算法。其本质是从高维数据空间学习出低维流形结构,给出有效的低维表示,利用重构映射f实现从样本数据{xi}中得到{yi}。其研究的基本内容有维数确定、目标维数和重构映射三个方面[4]。 1.2.2 拉普拉斯特征映射算法 LE算法的基本原理是高维空间中近距离点投影到低维空间中的像也应该离得很近[5]。其特点是Laplacian-Beltrami算子被运用到了LE算法中,该算子可由相邻图的加权拉普拉斯来近似,是一个被定义在切空间梯度向量上的散列函数。其算法描述如图2。 图2 拉普拉斯特征映射算法流程 采用二维全息谱和流形学习的主轴系统故障识别方法,首先需要对水平和垂直方向的信号进行归一化,获得规范化的数据,然后对归一化的信号进行降噪[6],得到二维全息谱,根据二维全息谱的椭圆信息对故障类型进行初步识别,对每个倍频的数据,采用构成每个椭圆的样本作为一个维度,构建高维特征空间,最后运用LE算法提取四个分倍频和高倍频的低维流形。 主轴系统不能人为设定故障进行数据采集,选择转子代替主轴为研究对象对主轴系统故障特征提取和识别方法进行实验验证。笔者用INV1612转子实验系统,如图3所示,可以完成转子的失衡、双稳态行为、横向裂纹、不对中故障、动静件碰摩等试验。 图3 INV1612转子实验系统 简化转子实验系统如图4,图中A,B,C,D为四个传感器,在两个轴承座的水平和垂直方向上安装。 图4 转子实验台系统图1.电机 2.电机座 3.联轴器 4,8.滚动轴承5,9.轴承座 6,7.圆盘转子 A,B,C,D.传感器 使用电涡流传感器分别采集转子水平和垂直方向的失衡、不对中、碰摩样本数据,采样频率为1 024 Hz,转速为960 r/min。由于转子的失衡、不对中和碰摩故障均属于高倍频故障,验证时运用LE算法只提取高倍频的低维流形,对转子故障进行识别。同理,对于转子分倍频的故障识别也可用该方法验证。 对转子实验台采集的失衡、不对中、碰摩信号进行归一化处理,然后去除信号中所包含的噪声及其他干扰。得到的二维全息谱图如图5所示。 图5(a)中,转子在失衡状态下的二维全息谱,在倍频处有较高的幅值,而且倍频处的椭圆较扁,可能存在支持刚度不对称,2倍频和高倍频的幅值逐渐降低,存在失衡故障。 图5 转子故障二维全息谱图 转子不对中的特征也以2倍频为主,并且不对中2倍频的椭圆较扁。转子不对中往往受到热变形、安装等很多因素的影响,其故障特征也易与其他的故障形成混淆。与不对中状态的谱特征非常相似的是轴向裂纹的故障特征,都是在二维全息谱出现2倍频异常,若2倍频较扁则为不对中故障,若较圆则为横向裂纹,但不对中故障的严重程度与2倍频成正比,因此轻微不对中往往易与裂纹混淆。图5(b)中,转子在1倍频处椭圆也较扁,说明转子受力不均、或者支撑刚度不均,转子在2倍频出离心率增大,并且2倍频分量的离心率趋近于1条直线,2倍频振幅明显大于倍频的振幅也是不对中故障的特征,而且2倍频和4倍频的椭圆较扁长轴方向垂直,属于典型的不对中故障,因此由二维全息谱可以初步判定为不对中故障。转子的碰摩也是转子中经常出现的故障,它是一种非线性现象,引起的是非线性振动。发生碰摩的部位可能是径向,也可能是轴向。轴向往往表现为有色噪声,径向在二维全息谱上表现为各倍频分量为互相平行的直线。转子故障总是与其他故障同时存在,最典型的是碰摩故障和部件松动故障非常类似。图5(c)中,二维全息谱中的高频分量为离心率较大的椭圆,长轴的方向也不确定,属于碰摩的故障特征,2倍频以后的振幅逐渐减小,属于失衡的故障特征,2倍频表现的椭圆较扁属于不对中的故障,单从全息谱的特征不易区分故障类型。 因此,为了进一步确定故障类型,运用LE流形学习算法提取不同倍频下的低维流形,以获取更为敏感的特征信号。设定LE的目标维数为2,采样点数为27,Sigma为10。其低维流形图如图6~8所示。 图6 LE提取转子的失衡状态高倍频的低维流形 图7 LE提取转子不对中状态高倍频的低维流形 由图6知,运用LE算法提取的各倍频的低维流形中,二维和三维流形均表现为1倍频,出现了与其他类型不同的低维流形特征,高倍频低维流形表现的特征基本相似。综合考虑转子状态出现的二维全息谱,可以得出,1倍频的低维流形反映了转子在运转过程中振幅突然变大,2倍频和更高倍频的低维流形反映了转子的振幅逐渐变小的振动特征,即证明转子的故障状态为失衡。 图7中,转子不对中状态在倍频、2倍频的二维全息谱的低维流形明显不同,与二维全息谱分析的结果结合对比,1倍频的低维流形反映了不对中状态轴向窜动的特征,2倍频的低维流形反映了转子不对中状态的振动特征,3倍频和4倍频表现出的特征相似。图8中,各倍频的低维流形都不相同,推断可能是由于椭圆信息中相位、振幅、离心率等中的某个指标的变化造成各倍频低维流形不同,结合二维全息谱各种故障状态所表现的特征,仅碰摩状态的离心率表现为转子碰摩状态在高倍频的二维全息谱的低维流形类似,与二维全息谱的故障理论结合,是由于离心率的不同导致各倍频处低维流形的不同,因此可以确定为碰摩状态。 图8 LE提取转子的碰磨状态高倍频的低维流形 二维全息谱算法在主轴系统故障识别上具有直观性等特点,但存在局限性,在某些情况下无法对主要的故障进行识别。将流形学习LE算法与二维全息谱相结合,弥补了全息谱的缺点,通过实验验证,该方法能够准确有效的提取和识别主轴系统故障特征。 [1] 吕善进.激光加工数控系统及状态监测技术研究[D].哈尔滨:哈尔滨工业大学,2007. [2] 屈梁生. 机械故障的全息诊断原理[M].北京:科学出版社,2007. [3] 陈维恒.微分流形初步[M].北京:高等教育出版社,2002. [4] Bennett R.S. The Intrinsic Dimensionality of Signal Collections [J].IEEE Transcations on Information Theoy,1969,15(5):517-525. [5] 徐 蓉,姜 峰,姚鸿勋. 流形学习概述[J].智能系统学报,2006,1(1):44-51. [6] 吴 伟,蔡培升.基于MATLAB的小波去噪仿真[J].信息与电子工程,2008(3):220-229. One Method of Fault Identification for Spindle System ZHAO Chuan1, WANG Hong-jun1, ZHANG Huai-cun2 (1.TheKeyLaboratoryofModernMeasurementandControlTechnologyAffiliatedtotheMinistryofDucation,BeijingInformationScienceandTechnologyUniversity,Beijing100019,China; 2.CollegeofMechanicalandElectricalEngineering,BeijingInformationScienceandTechnologyUniversity,Beijing100019,China) 2014-07-03 北京市教育委员会科技发展计划重点项目(编号:KZ201211232039) 赵 川(1988-),男,河北秦皇岛人,研究生,研究方向:机械制造及自动化。 TH165.3 A 1007-4414(2014)04-0024-04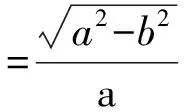
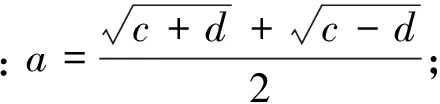
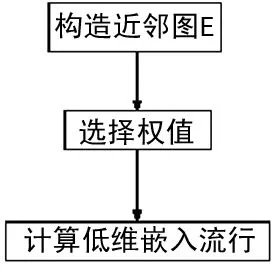
2 基于二维全息谱和流形学习的主轴系统故障识别
3 实验验证

4 结 语

