粗糙度对接触界面动态特性的影响研究*
郑淑丽
(1.长沙理工大学 汽车与机械工程学院, 湖南 长沙 410076; 2.长沙职业技术学院 机械工程系, 湖南 长沙 410217)
粗糙度对接触界面动态特性的影响研究*
郑淑丽1,2
(1.长沙理工大学 汽车与机械工程学院, 湖南 长沙 410076; 2.长沙职业技术学院 机械工程系, 湖南 长沙 410217)
接触界面的刚度和阻尼对机械结构的动态特性有重要影响,为了描述接触界面粗糙度对机械结构动态特性的影响,建立了振动应力波在粗糙接触界面传播的数学模型,并进行了数值仿真和模型试验。试验结果表明:较小的表面粗糙度有利于振动应力波通过接触界面传播;随着粗糙度值的增加,通过接触界面的振动应力波减少,说明较大的粗糙度界面消耗振动能量,但是产生了高次谐波,使振动状态变得复杂。
粗糙度 应力波 接触界面 能量耗损
Abstract: Contact interface stiffness and damping have an important influence on dynamic characteristics of the mechanical structure. In order to study on contact interface rough effect on dynamic characteristic of machinery, the model of vibration stress wave propagation was established in this paper. The test results show that small surface rough is benefit for vibration stress wave reducing through contact interface, with the surface rough increase, vibration stress wave reducing through contact interface. The larger roughness is benefit to impede vibration stress wave propagation at contact interface, but higher harmonic would be produced and the vibration state becomes complicated.
Key words: rough; stress wave; contact interface; energy dissipation
0 引 言
机械结构一般采用螺栓、销轴、铆接和焊接等方式组合而成,在连接处存在一个接触界面。由于接触界面处材料和力学性能的不连续,接触界面刚度和阻尼发生变化,影响机械结构的动态特性。随着机械结构向大型化发展,机械结构的振动控制问题也越来越突出。
如何减小振动应力波在机械结构中的传播,大量专家和学者进行了研究。黄毅等[1]人采用独立模态空间控制方法对泵送状态下的混凝土泵车臂架结构响应进行了主动控制研究,水平工况时振动幅度减小了80%。侯守武等[2]应用机械导纳理论,推导了布设方钢的无限板在点激励作用下的振动响应方程,发现单级方钢或多级平行方钢平板结构目标区的振动级落差随振源距离的增大逐渐减小,远离振源靠近对称轴附近的目标区的振动有所放大;不平行方钢改变了平板振动对称分布的特性,改变方钢的不平行度可提高减振效果。万浩川等[3]基于粘弹性阻尼材料具有小变形下高阻尼的特点,提出了粘弹性材料阻尼结构设计的基本思想和过程,建立粘弹性阻尼结构的有限元模型,对比分析了阻尼结构的减振性能。仿真结果说明,粘弹性阻尼结构对振动有明显衰减。
笔者从应力波在接触界面传播的角度进行研究。应力波在各向同性材料中传播部件中传播时,当应力波幅度较小,并在内部传播时呈现线性特性。应力波在机械结构中传播要经过不同部件之间的接触界面,由于接触界面处材料、特性等的变化,使应力波在接触界面的行为十分复杂,具有非线性特性[4-5]。
1 应力波在接触界面传播
由于介质表面粗糙度的存在,接触界面处存在大量的空隙,如图1所示。在接触点处,固体介质Ⅰ和固体介质Ⅱ接触,在空隙处,介质Ⅰ或介质Ⅱ和空气接触。由于空气的特性阻抗远小于固体介质的特性阻抗(约为1%),所以在空气和固体介质的接触界面,应力波只发生反射,无透射。在两种固体介质的接触点处会根据两种接触介质特性阻抗比,发生反射和透射,有一部分应力波通过接触界面透射入到介质Ⅱ中。所以在入射介质Ⅰ中,存在入射应力波和反射应力波。在介质Ⅱ中形成透射应力波。

图1 应力波通过粗糙接触界面
机械结构的每个表面都是经过机械加工的,具有一定的粗糙度,用来支撑机械载荷的面积仅仅是名义接触面积的很小部分,所以接触界面的接触不完整而导致应力波通过接触界面后振动能量和振动幅度减小,即:在接触界面处产生明显的能量损失,成为界面阻抗。窗体顶端。
2 粗糙度模型
为了研究接触界面粗糙峰在载荷作用下的变形规律,先研究单个粗糙峰在载荷作用下的变形。将粗糙度凸起假设成圆球,与一个刚性平面接触,在外载荷W的作用下,粗糙度凸起发生变形[6],如图2。
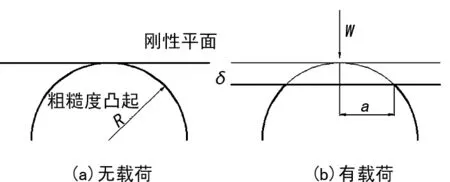
图2 接触界面模型
(1) 弹性接触
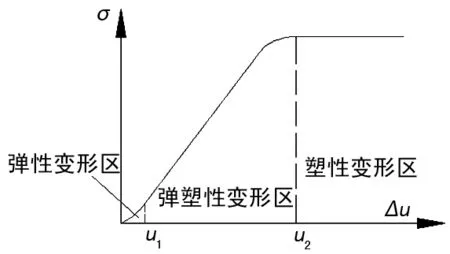
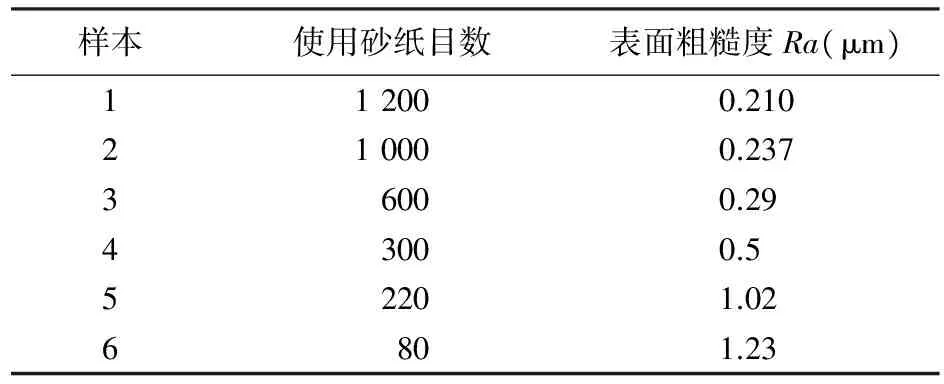
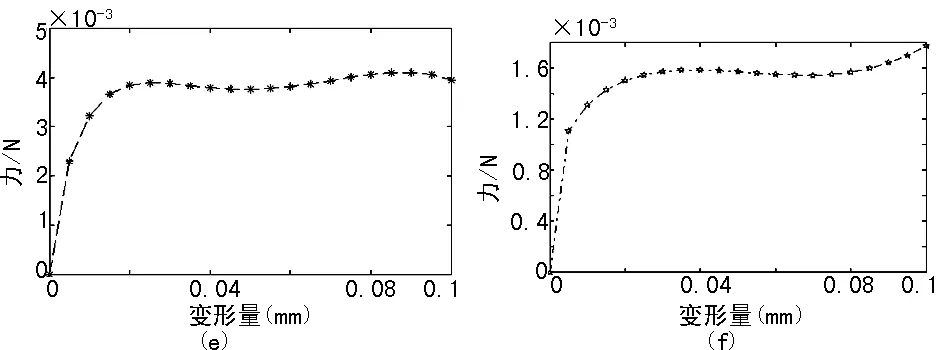
当接触界面之间的相对位移足够小(Δu (1) 法向接触刚度为应力对变形的导数,为: (2) 从式(2)可看出单个微凸体的接触界面刚度和两接触材料的接触模量和泊松比有关,也和两接触面接触时的变形情况有关。其中,当两接触材料确定后,在外界载荷加载频率不变的情况下,那么接触界面刚度也就只与两接触面的变形情况有关。 (2) 完全塑性接触 当接触界面的相对位移足够大(Δu≥u2)(u2为接触界面发生塑性变形时的接触界面位移)时,微凸体将发生完全塑性变形。在这一阶段,接触界面之间的应力等于软材料的硬度H,即 σ=H (3) 则接触界面的刚度为: K=0 (3) 弹塑性接触 当接触界面的相对位移u1<Δu≤u2时,微凸体既存在弹性变形也发生塑性变形,即发生弹塑性变形,这一阶段微凸体接触面积和接触压力与法向变形量的关系将变得极为复杂。当出现初始屈服(Δu=u1)时,塑性变形发生在接触面积中心点以下一定深度一个微小的体积内,因而塑性变形区被体积大的多的弹性变形区所完全包围,且实际接触面积内每一点仅发生弹性变形而无塑性变形。因此在初始屈服临界点,接触面积和接触压力的变化应该是连续和光滑的。同理,在完全塑性变形临界点(Δu=u2),接触面积内弹性变形部分极少,而绝大部分发生的是塑性变形,故此临界点处的接触面积和接触压力也应该仅发生连续和光滑地变化,不应有突变。这种连续和光滑条件意味着弹塑性区间的实际接触面积和平均接触压力在初始屈服(Δu=u1)点应分别等于弹性接触面积和平均接触压力,在完全塑性屈服点应分别等于塑性接触面积和平均接触压力,而且它们的导数在此两临界点也应分别相等。满足这些边界条件的弹塑性区间的接触面积和平均接触压力可分别用以Δu为自变量的且为单调增加的两个多项式表示。为了构造这两个多项式首先考察如下样板函数[8-10]: (4) 该函数在区间[0,1]内单调增加,且: f(u1)=0,f(u2)=1 f′(u1)=f′(u2)=0 如有两个函数: y=Q(Δu), 0≤Δu≤u1 y=S(Δu),u2≤Δu≤+∝ 则可以证明,与此两函数在u1和u2临界点连续且光滑连接的函数可用包含上述样板函数的下列方程式表示,即: y=Q(Δu)+[S(Δu)-Q(Δu)]f(Δu) (5) 根据在u1和u2点应力连续可以推出: (6) 则接触界面的刚度为: (7) 接触界面的应力和变形之间的关系,如图3。 图3 界面变形和应力之间的关系 当接触界面的载荷从零开始增加时,只有接触界面中最高的粗糙峰进入接触,并进入弹性变形,由于接触的粗糙峰数量较少,随着接触界面载荷的增大,所以接触界面粗糙峰的接触应力迅速达到材料的屈服极限,进入塑性变形状态,接触粗糙峰在载荷作用下迅速变形,接触面积迅速增大,并且使其他较高的粗糙峰进入接触,参与接触的粗糙峰迅速增多,接触面积迅速增大,通过接触界面的应力波迅速增多,进入弹塑性变形阶段随着接触界面载荷的进一步增大,参与接触的粗糙峰增多,部分接触粗糙峰处于塑性变形状态,部分接触粗糙峰处于弹性变形状态,接触界面进入弹性变形和塑性变形的混合状态,接触界面位移变化速度降低,接触面积增大速度降低,通过接触界面的应力波增加速度降低;随着载荷的进一步增加,进入接触的粗糙峰数量进一步增多,当载荷足够大时,所有的粗糙峰全部进入塑性变形状态,粗糙峰的接触界面增加速度降低,通过接触界面的应力波增多速度进一步变慢,最后不再增加。 采用不同型号砂纸打磨钢板,采用测量粗糙度值,结果如表1所列。与某光滑平面接触后在万能压力机作用下,测试接触界面变形量与施加力之间的关系,如图4所示。 表1 样本粗糙度 图4 接触界面力-变形曲线 从图4可看出不同粗糙度的接触界面在界面变形量相同条件下,施加力的过程不一致。图4(a)、(b)和(c)表示随着力的增大,接触界面表形增大,即界面刚度逐渐增大,开始段由于只有部分粗糙凸起参与接触,使界面位移增长速度迅速,随着参与接触的粗糙度凸起增多,变形量增加缓慢,即接触界面刚度逐渐增加;图4(d)所示的接触界面力和变形量成正比关系,说明接触界面刚度为恒定值;图4(e)、(f)接触界面施加力先快速增大,然后增加速度降低,之后出现小幅度震荡,说明此类接触界面为逐渐软化界面,即界面产生弹塑性变形,损失部分能量。 随着接触界面粗糙度的增大,接触界面刚度逐渐减小,阻尼逐渐增大,损失部分能量。当粗糙度达到一定值时,接触界面产生震荡,即高次谐波,对机械结构动态性能影响较大,应使机械结构避免这种状况。 [1] 黄 毅,吴斌兴,王佳茜.混凝土泵车臂架振动响应的主动控制实验研究[J].振动与冲击,2012,31(2):91-94. [2] 侯守武,焦映厚,陈照波,等.基于机械导纳理论的方钢结构减振特性[J].吉林大学学报(工学版),2013(5):1295-1301. [3] 何周理,徐 绯. 粘结带模型在界面强度分析中的应用[J].机械科学与技术,2010,29(10):1342-1345. [4] 隆志力,韩 雷,吴运新,等.芯片键合换能系统中接触界面的影响分析[J].压电与声光,2008,30(8):511-513. [5] 申昭熙.含弱界面复合材料层合板中弹性波传播行为研究[D].西安:西安交通大学,2004. [6] Lei Han, Jue Zhong, Gongzhi Gao. Effect of Tightening Torque on Transducer Dynamics and Bond Strength in Wire Bonding[J]. Sensors and Actuators A, 2008(141):695-702. [7] 凤飞龙,沈建中,邓京军. 用二维等效电路模型研究大截面圆柱变幅杆的振动[J]. 声学技术, 2007, 26(1): 149-152. [8] Michael Mcbreaty, Lee H. Kim, Nihat M, et al. Analysis of Impedace Loading in Ultrasonic Transducer System[J]. Ultrasonic Symposium, 1997:497-504. [9] 赵 波,范平清.盘式制动器的制动效能和接触应力分析[J].机械设计与制造,2011(9):134-136. [10] 湛利华.界面接触热阻实验与建模及其在快凝铸轧参数设计中的应用[D].长沙:中南大学,2001. Study of Rough Effect on Dynamic Characteristic of Contact Interface ZHENG Shu-li1,2 (1.InstituteofAutomobileandMechanicalEngineering,ChangshaUniversityofScienceandTechnology,ChangshaHunan410076,China; 2.MechanicalEngineeringDepartment,ChangshaVocational&TechnicalCollege,ChangshaHunan410217,China) 2014-05-26 国家自科基金(编号:50605064)、湖南省教育厅项目(编号:14C0026);工程车辆轻量化与可靠性技术湖南省高校重点实验室开放基金(编号:2013KFJJ0) 郑淑丽(1981-),女,辽宁喀左人,工程师,硕士,研究方向: 机械结合面特性辨识。 TH117 A 1007-4414(2014)04-0001-03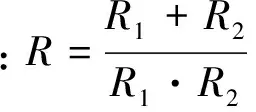
3 试验研究


4 结 语

