网络结构的边毁裂度
刘二强,李银奎
(青海民族大学数学与统计学院,青海 西宁 810007)
网络结构的边毁裂度
刘二强,李银奎
(青海民族大学数学与统计学院,青海 西宁 810007)
在毁裂度的基础上,研究图的边的毁裂度.通过优化组合、归纳假设的方法界定了图的边毁裂度的值,如笛卡尔积图:Pm×Pn,Pm×Cn,Cm×Cn,Km×Kn,并界定了G=G1×G2的边毁裂度的界.最后给出了一些基本图,如路、圈、星图、完全二部图Km,n的线图边毁裂度.
边毁裂度;笛卡尔积图;线图
1 引言
特高压交流电网不但要求稳定可靠、不容易被破坏,而且要求特高压交流网络一旦被毁后能够容易确定位置,且极易修复.借助图的连通参数讨论图网络的稳定性,对于在复杂电网中的应用有特殊意义.文献[1-8]引入了如边连通度、边坚韧度、边完整度、离散度、边粘连度等一些不错的刻画参数,只是每个参数都有各自的局限性.图的边毁裂度是一个新的度量参数(文献[8]),对于图网络的刻画也有一定的影响.本文进一步的探讨了路、圈、完全图在笛卡尔积下的图的边毁裂度以及路、圈、星图、完全二部图Km,n在线图下的边毁裂度.
设图G=(V,E),S⊆E(G),用w(G−S)表示G−S的连通分支数,τ(G−S)表示图G−S的最大连通分支的阶数.图的边毁裂度定义为:
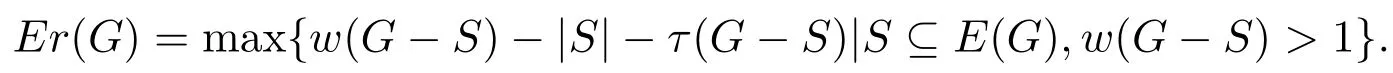
对于一个边集S⊆E(G),如果w(G−S)−|S|−τ(G−S)=Er(G),称S为G的一个Er−集.文中讨论的图均为简单、无向图,未提及的术语及定义见文献[7].
2 一些笛卡尔积图的边毁裂度结果
定义 2.1[8]连通图G1与G2的笛卡尔积G1×G2是连通图且对 u1,v1∈V(G1),u2,v2∈V(G2),((u1,u2),(v1,v2))∈E(G1×G2)⇔ 或者 u1=v1,且(u2,v2)∈E(G2),或者u2=v2,且(u1,v1)∈E(G1).
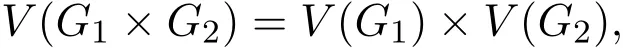
Pm×Pn构造的网络图可以看作是一顶点数为m×n的平面网格.
定理2.1连通图G是Pm×Pn,则Er(G)=m+n−mn−1.
证明取G任一边割集S.
情形 1S∩E(Pm)/=∅,S∩E(Pn)=∅.
(1)w(G−S)=2,n≤|S|≤2n−1,因此有
w(G−S)−|S|−τ(G−S)=2−|S|−(mn−n)=2+n−mn−|S|,
显然当|S|=n时,w(G−S)−|S|−τ(G−S)=2+n−mn−n=2−mn为最大值.重复这一做法,可得:
(2)2 当w(G−S)=m时,w(G−S)−|S|−τ(G−S)=m−(m−1)n−n=m−mn.根据边毁裂度定义可得Er(G)=m−mn. 情形 2S∩E(Pm)=∅,S∩E(Pn)/=∅,同情形1,不再证明. 情形 3S∩E(Pm)/=∅,S∩E(Pn)/=∅. 取边求边毁裂度最好的方法是分层去边(Pn∪n为一层,边数为2n−1). (1)w(G−S)=2,2≤|S|<4,因此有 w(G−S)−|S|−τ(G−S)=2−|S|−(mn−1)=3−mn−|S|, 显然当|S|=2时,w(G−S)−|S|−τ(G−S)=3−mn−2=1−mn为最大值.重复这一做法,可得: (2)2 接下来再去一条边就可以增加一分支,即 w(G−S)=n+1,|S|=n+(n−1)=2n−1,τ(G−S)=mn−n, w(G−S)−|S|−τ(G−S)=n+1−(2n−1)−(mn−n)=2−mn. 这样第一层边全部去掉,当w(G−S)=n+1时,边毁裂度为这一层最大值. 整个Pm×Pn图中共有 m−1个这样的层数,同上重复按层去边,每层边取完时的边毁裂度最大,当去掉 m−1层的边数后,整个图形变为 mn−n个孤立点和一条 Pn.此时w(G−S)=mn−n+1,图的边毁度为: w(G−S)−|S|−τ(G−S)=mn−n+1−{(m−1)n+(n−1)m−(n−1)}−n=m−mn. (3)mn−n+1 w(G−S)=mn时,w(G−S)−|S|−τ(G−S)=mn−{(m−1)n+(n−1)m}−1=m−mn.根据边毁裂度定义可得Er(G)=m+n−mn−1. Pm×Cn构造的网络图可以看作是一顶点数为m×n的圆柱网格. 定理2.2连通图G是Pm×Cn(m≥2,n≥3),则 证明取G任一边割集S. 情形 1S∩E(Pm)/=∅,S∩E(Cn)=∅. 若2≤w(G−S)≤m,每增加一个分支时,要多去掉n条边,相应地最大阶数减少n.因此w(G−S)−|S|−τ(G−S)随着分支数的增加,是单调增的,当分支数取到最大值时,边毁裂度取到最大值,因此w(G−S)=m时, 根据定义可得Er(G)=m−mn. 情形 2S∩E(Pm)=∅,S∩E(Cn)/=∅. (1)w(G−S)=2,2m≤|S|≤3m−1,因此 显然当|S|=2m时, 重复这一做法,可得: (2)2≤w(G−S)≤n,每增加一个分支时,要多去掉m条边,相应地最大阶数减少m.因此w(G−S)−|S|−τ(G−S)随着分支数的增加,是单调增的,当分支数取到最大值时,边毁裂度取到最大值,因此w(G−S)=n时,w(G−S)−|S|−τ(G−S)=n−mn−m.根据定义可得Er(G)=n−mn−m. 情形 3S∩E(Pm)/=∅,S∩E(Cn)/=∅. 取边求边毁裂度最好的是分层去边(Cn∪n为一层,边数为2n). (1)2≤w(G−S)≤n,每增加一个分支时,要多去掉2条边,相应地最大阶数减少1.所以w(G−S)−|S|−τ(G−S)随着分支数的增加,是不变的.接下来再去一条边就可以增加一分支,即 这样第一层边全部去掉,当w(G−S)=n+1时,边毁裂度为这一层最大值. Pm×Cn图中剩下m−1层,同上重复按层去边,每层边取完时的边毁裂度最大,当去掉m−1层的边数后,整个图形变为mn−n个孤立点和一个Cn.此时w(G−S)=mn−n+1,图的边毁度为: (3)mn−n+1 根据边毁裂度定义可得Er(G)=n−mn−1. 由于m≥2,n≥3,显然情形2中的Er(G)结果不是最好的,情形1与情形3中的Er(G)结果在下面两种情况下分别是最好的. 当n−1≥m,即n≥m+1时,Er(G)=n−mn−1是最好的. 反之,当n−1 定理2.3连通图G是Cm×Cn(m,n≥3),则 证明取G任一边割集S. 情形 1S∩E(Cm)/=∅,S∩E(Cn)=∅. (1)w(G−S)=2,2n≤|S|≤3n−1,有 w(G−S)−|S|−τ(G−S)=2−|S|−(mn−n)=2+n−mn−|S|, 显然当|S|=2n时,为最大值.重复这一做法,可得: (2)2 因此根据定义可得,Er(G)=m−mn−n. 情形 2S∩E(Cm)=∅,S∩E(Cn)/=∅,情形2与情形1相同,因此不再讨论. 情形 3S∩E(Cm)/=∅,S∩E(Cn)/=∅. (1)w(G−S)=2,4≤|S|<7,有 显然当|S|=4时,为最大值.重复这一做法,可得: (2)2 当w(G−S)=n时,|S|=3n−2,τ(G−S)=mn−(n−1),因此有 接下来再去掉2条边,就可以得到一个分支,相应地最大阶数减少1.此时w(G−S)= n+1,|S|=3n,τ(G−S)=mn−n, w(G−S)=n+1,第一层边数已经取完,易观察到剩余阶数大的部分是圆柱网格相当于Pm−1×Cn.因此接下来求边毁裂度是分层去边. 重复以上做法,知Pm−1×Cn图中共有m−2个这样的层数,根据定理2.2,重复按层去边,每层边取完时的边毁裂度最大,当去掉m−1层的边数后,整个图形变为mn−n个孤立点和一个Cn.此时w(G−S)=mn−n+1,图的边毁度为: (3)mn−n+1 Cm×Cn与Cn×Cm得到的图是相同的,情形1与情形2得到的结果其实可以看作是相同的,所以取情形1中得到的结果.情形1与情形3得到的结果在下面两种情况下分别是最好的. 当n−1≥m,即n≥m+1时,Er(G)=−mn−1是最好的. 反之,当n−1 定理2.4连通图G是Km×Kn(m,n≥3),则 证明过程同定理2.2,定理2.3.不再赘述. 在笛卡尔积图中发现,边毁裂度越小,图的结构越复杂,图就越稳定,越不容易被破坏.这种图网络的抗毁性最好.在笛卡尔积图中,Pm×Pn的图结构是最简单的,这种图网络抗毁性最差,最容易被破坏;Km×Kn的图结构是最复杂的,也是最稳定的,网络抗毁性最好.所以结合定理2.1,定理2.2,定理2.3,定理2.4,有下面的推论: 推论2.1设G=G1×G2,则5−(mn+m+n)≤Er(G)≤−1. 注 2.1当P2×P2时,图为圈,恰好取到上界-1.当Km×Kn且m≥4时,恰好取到下界. 引理3.1G是树当且仅当Er(G)=0. 引理3.2设G为n阶的圈,则Er(G)=−1. 引理3.3G是完全图Kn(n≥5),则Er(G)=4−2n. 定义 3.1[9]一个图G的线图L(G),它的顶点是图G的边,任意两个点之间相邻,当且仅当图G中相应的边之间是相邻的. 推论3.1图G是n阶的路Pn,则Er(L(G))=0. 证明因为G的线图L(G)显然仍是一条路,且L(G)=Pn−1.根据引理3.1,Pn是树,显然有Er(Pn)=0.所以Er(L(G))=0. 推论3.2图G是n阶的圈Cn,则Er(L(G))=−1. 证明因为G的线图L(G)显然仍是一个圈,且L(G)=Cn.根据引理3.2,显然Er(Cn)=−1.所以Er(L(G))=−1. 推论3.3图G是n+1阶的星图K1,n,则Er(L(G))=4−2n(n≥5). 证明因为G的线图L(G)是一个完全图, 当n=2时,K1,2的线图L(K1,2)=P2,所以Er(L(K1,3))=0; 当n=3时,K1,3的线图L(K1,3)=C3,所以Er(L(K1,3))=−1; 当n=4时,K1,4的线图L(K1,4)=K4,很容易得出Er(L(K1,4))=−3; 当n≥5时,K1,n的线图L(G)=Kn,根据引理3.3,所以Er(L(G))=4−2n. 推论3.4图G是完全二部图Km,n,则 证明易知L(G)=Km×Kn,因此图G的线图的边毁裂度相当于Km×Kn的边毁裂度.根据定理2.5,得到上面结果. [1] Li Y,Zhang S,Li X.The rupture degree of graphs[J].International Journal of Computer Mathematics, 2005,82(7):793-803. [2] 武燕,魏暹荪.关于图的边粘连度[J].工程数学学报,2004,21(5):704-708. [3] 陈忠,李银奎.完全k叉树的粘连度[J].纯粹数学与应用数学,2013,29(5):484-488. [4] 李银奎,段宝荣,陈忠.完全k叉树的离散数和完整度[J].纯粹数学与应用数学,2011,27(3):285-291. [5] K S Bagga,L W Beineke,M I Lipman,R E Pippert.Edge-integrity:a Survey[J].Discrete Math.,1994,124: 3-12. [6] B L Piazzal,F S Roberts,S K Stueckle.Edge-tenacious networks[J].Networks,1995,25:7-17. [7] 邦迪J A,默蒂U S F.图论及其应用[M].北京:科学出版社,1984. [8] 李银奎.图的连通参数的相关研究[D].西安:西北工业大学,2003. [9] 李学良,刘艳.路图与线图的一个综述[J].工程数学学报,2007,05:761-787. The edge rupture degree of network structure Liu Erqiang,Li Yinkui This paper is based on the rupture degree,and researches the edge rupture degree of graphs.By methods of optimized combination,inductive hypothesis,de fi ne the edge rupture degree of graphs.Such as the Cartesian product graphs:Pm×Pn,Pm×Cn,Cm×Cn,Km×Kn,and de fi ne the bound of edge rupture degree of G=G1×G2.At last,discussed the rupture degree of line graph of some graph classes,such as paths,circle,star graph,complete bipartite graph Km,nand so on. the stability of network,edge rupture degree,the cartesian product graph,line graph O157.5 A 1008-5513(2014)04-0428-07 10.3969/j.issn.1008-5513.2014.04.013 2014-05-19. 教育部“信息网络抗毁性与嵌入式理论研究”(Z2010007);青海民族大学“基于抗毁性的网络结构优化研究”(xjz201403). 刘二强(1988-),硕士,研究方向:图论与网络优化. 2010MSC:05C15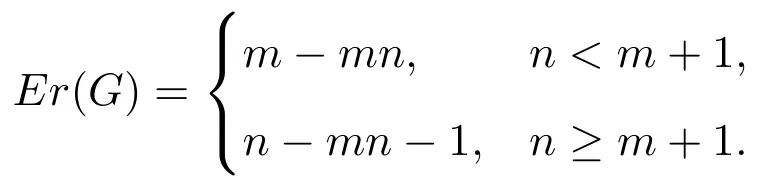
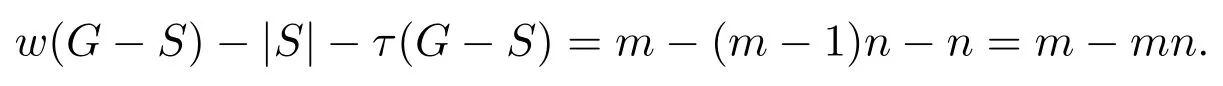
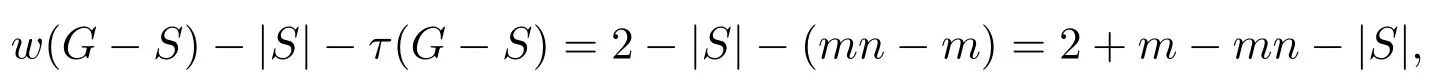


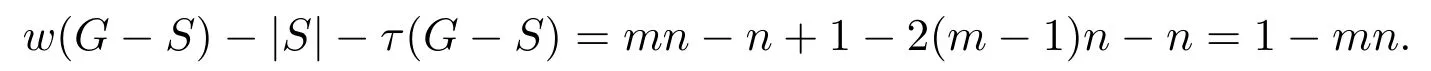
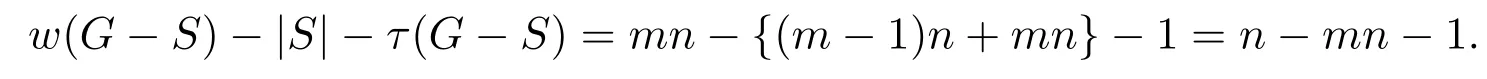
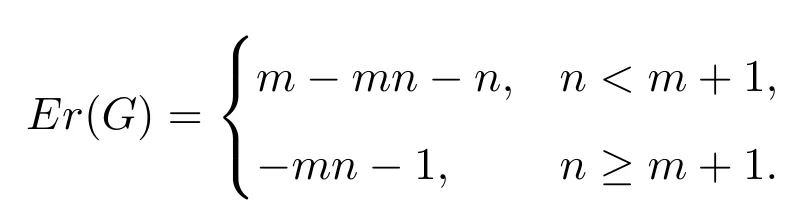
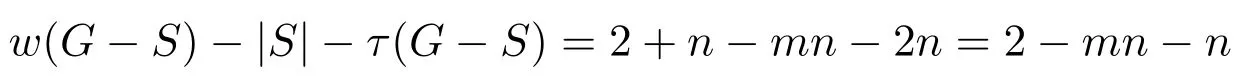
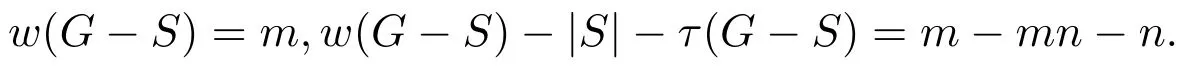
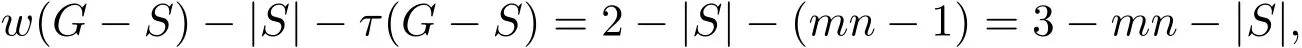
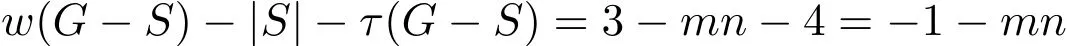

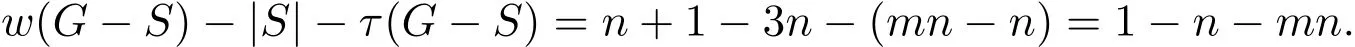
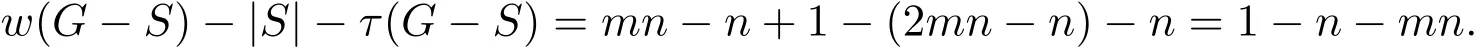

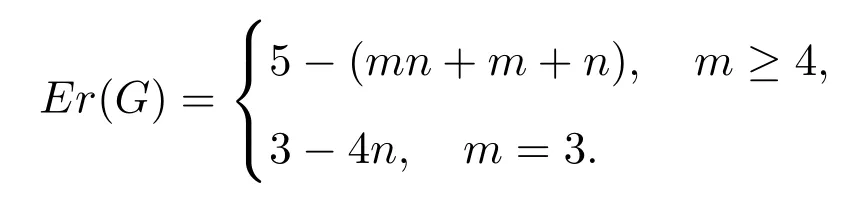
3 一些线图的边毁裂度的结果
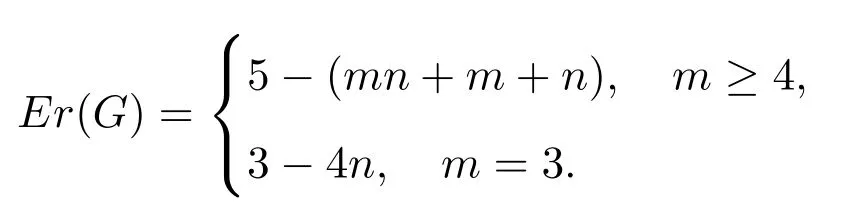
(School of Mathematics and Statistics,Qinghai Nationalities University,Xining 810007,China)

