On Uniform Decay of Solutions for Extensible Beam Equation with Strong Damping

FENG Bao-wei,ZHANG Ming,LIANG Tie-wang,LI Hai-yan

(1.College of Economic Mathematics,Southwestern University of Finance and Economics,Chengdu 611130,China;2.College of Information Science and Technology,Donghua University,Shanghai201620, China;3.Department of Inforwation and Arts Design,Henan Forestry Vocational College,Luoyang 471002,China)

On Uniform Decay of Solutions for Extensible Beam Equation with Strong Damping

FENG Bao-wei1,ZHANG Ming2,LIANG Tie-wang3,LI Hai-yan2

(1.College of Economic Mathematics,Southwestern University of Finance and Economics,Chengdu 611130,China;2.College of Information Science and Technology,Donghua University,Shanghai201620, China;3.Department of Inforwation and Arts Design,Henan Forestry Vocational College,Luoyang 471002,China)

This paper investigates the existence and uniform decay of global solutions to the initial and boundary value problem with clamped boundary conditions for a nonlinear beam equation with a strong damping.

extensible beam equation;global existence;uniqueness;uniform decay

§1. Introduction

In this paper we study a nonlinear extensible beam equation with a strong damping

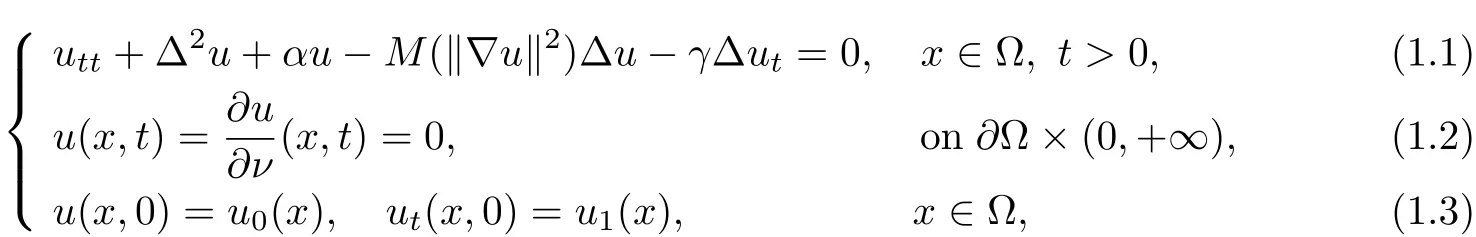
whereαandγare positive constants,Ω⊆ℝn(n≥1)is a bounded domain with smooth boundary∂Ω,νis the unit outward normalon∂Ω.Here M(·)is a function.

In recent years,many mathematicians have paid their attention to the global wellposedness and energy decay for nonlinear wave equations,hyperbolic systems and viscoelastic equations. Firstly,we recall some results concerning extensible beam equations.In 1950,Woinowsky-Krieger[1]proposed the one-dimensional nonlinear equation of vibration of beams,which is given by

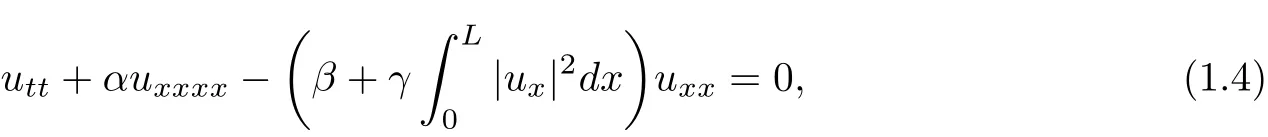
where L is the length of the beam andα,β,γare positive physical constants.The nonlinear part of(1.4)represents for the extensible eff ect for the beam whose ends are held a fixed distant apart in its transverse vibrations.In 1970s,mathematical analysis for global existence and asymptotic behavior of these extensible beams have been studied by Ball[23],Dickey[4], Medeiros[5]and the references therein.

The general form of(1.4)reads

where M(·)is a function satisfying some conditions.When functions f,g,h=0 in(1.5),many researches have been devoted to the study ofextensible beam equations,see,e.g.,Brito[6],Ma[7], Oliveira and Lima[8],Rivera[910],etc.Patcheu[11]studied the existence and decay property of global solutions to the Cauchy problem of(1.5)at the abstract level with f=0.Tusnack[12]investigated(1.5)with clamped boundary conditions and f=0 and obtained the exponential decay of the energy when a damping of type a(x)utis effective near the boundary.Cavalcanti et al[13]investigated the global existence and asymptotic behavior of the initial and boundary value problem of(1.5)with clamped boundary conditions.They established the globalexistence of solutions by the fixed point theorem and continuity arguments.They proved that the IBVP possesses a unique globalweak solution u,with(u,ut)∈C(ℝ+;H20×L2),provided that M∈C1,

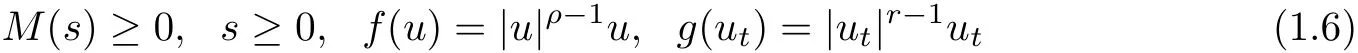
with 1＜ ρ,r≤ n/n−2 if n≥ 3;ρ,r＞ 1 if n=1,2.Under the basic research in[13], Ma and Narciso[14]subsequently studied the existence of global attractor to the IBVP of(1.5), with clamped boundary conditions.Recently,Yang[15]studied the global existence,stability and long time dynamics of solutions to the IBVP of(1.5).The author proved the IBVP is globally well-posed provided that either the growth exponent p of the source term f(u)is nonsupercritical or p is supercritical but is dominated by the growth exponent q of the nonlinear damping g(ut).Moreover,the author also investigated the existence offinite-dimensionalglobal attractors and exponential attractors.For the related work,one can refer to[16-19]and the references therein.

To our best knowledge,the global existence for extensible beam equations with a strong damping were not previously considered.So,the objective of this work is to establish the global existence and uniqueness of initial boundary value problem(1.1)～(1.3)with clamped boundary conditions.Moreover,we discuss the uniform decay of energy.

The outline of this paper is as follows.In Section 2,we give some preparations for our consideration and our main result.The statement and the proof of our main result will be given in Section 3.

§2.Preliminaries and Main Result

In this section,we give some preparations for our consideration and our main result.

We define

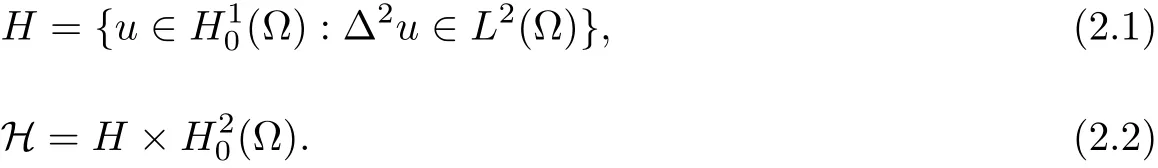
We assume M(·):ℝ+→ℝ+is a C2function satisfying

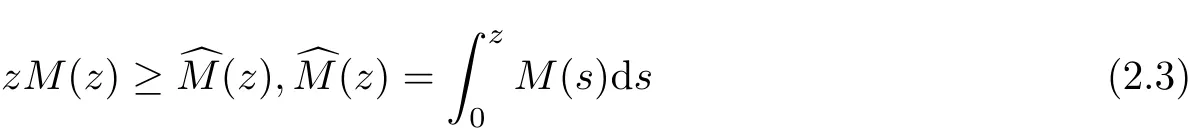
(if M(z)is monotone nondecreasing).

The energy of problem(1.1)～(1.3)is given by

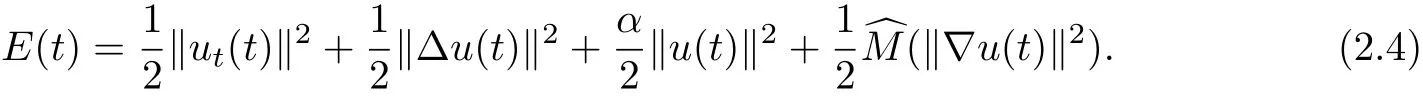
For convenience,we denote the norm and scalar product in L2(Ω)by‖·‖and(·,·),respectively.C1denotes a general positive constant,which may be different in different estimates.

Now we are in a position to state our main result.

Theorem 1 Let(2.3)hold.Ifthe initialcondition(u0,u1)∈H,then problem(1.1)～(1.3) admits a unique strong solution to(u(t),ut(t))∈H,such that for any t＞0,

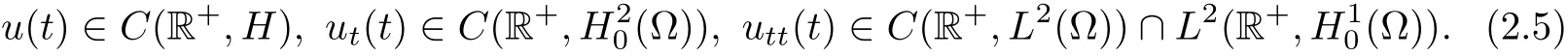
Moreover there exist positive constants C2and C3such that the energy E(t)of problem (1.1)～(1.3)satisfies

§3.Proof of Main Result

In this section,we are going to complete the proof of Theorem 1.Firstly,we show the global existence and uniqueness of solutions for problem(1.1)～(1.3).

Using the similar method as in[13],we can establish the global existence of solution (u(t),ut(t))∈H with a minimalmodification,we omit the detailed proofand(2.5)can also beobtained.Next we prove the uniqueness of solutions.

Let(u(t),ut(t))and(v(t),vt(t))be two global solutions of problem(1.1)～(1.3)with respect to initial data(u0,u1)and(v0,v1)respectively.Letω(t)=u(t)−v(t).Thenω(t)verifies

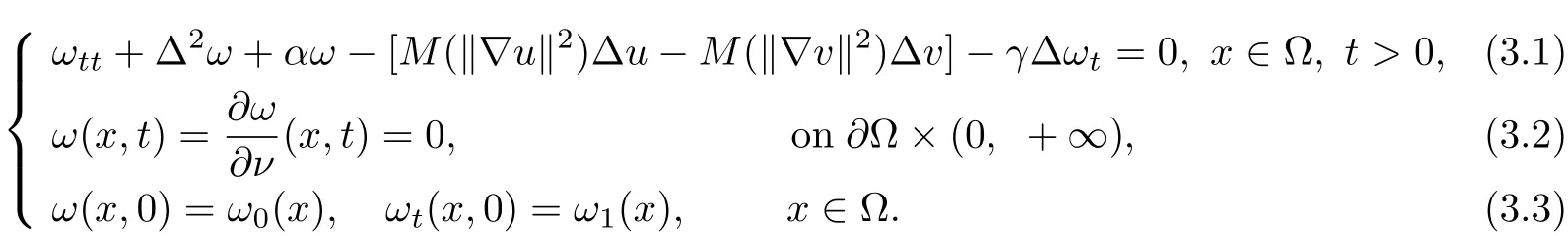
Multiplying(3.1)by utand integrating the result overΩwith respect to x,we have

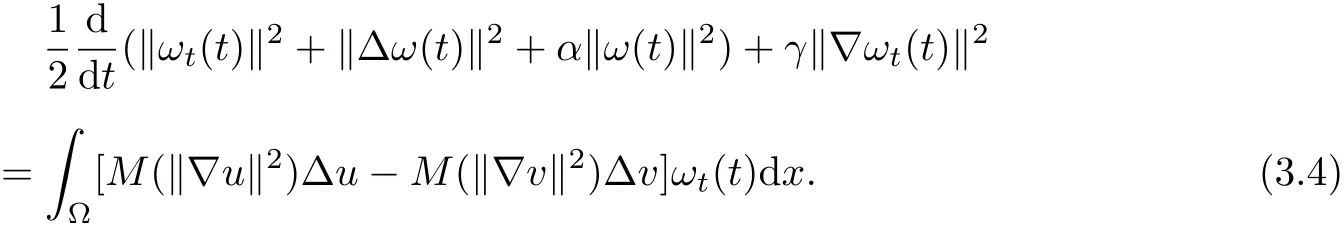
The direct computation gives

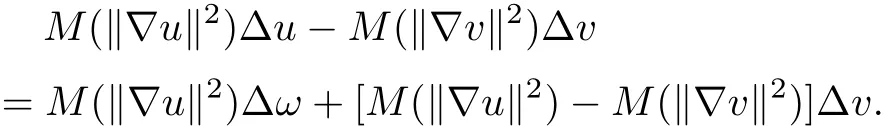
It follows from(2.5)that

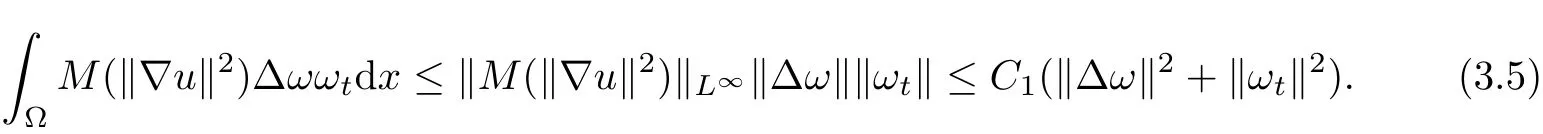
Noting that the interpolation inequality

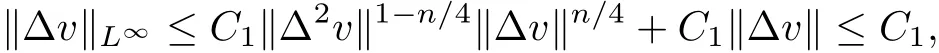
we can get

whereξ1=θ‖▽u‖2+(1−θ)‖▽v‖2andθ∈(0,1).Then we see that

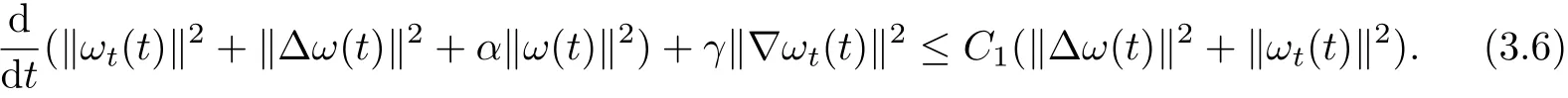
Differentiating(3.1)with respect to t,multiplying the result byωttand integrating by parts overΩ,we arrive at

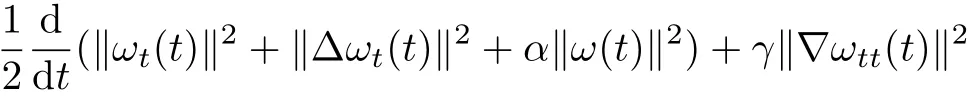
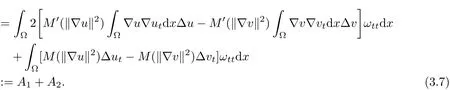
It is easy to see that

By H¨older’s inequality,the interpolation inequality and(2.5),we conclude

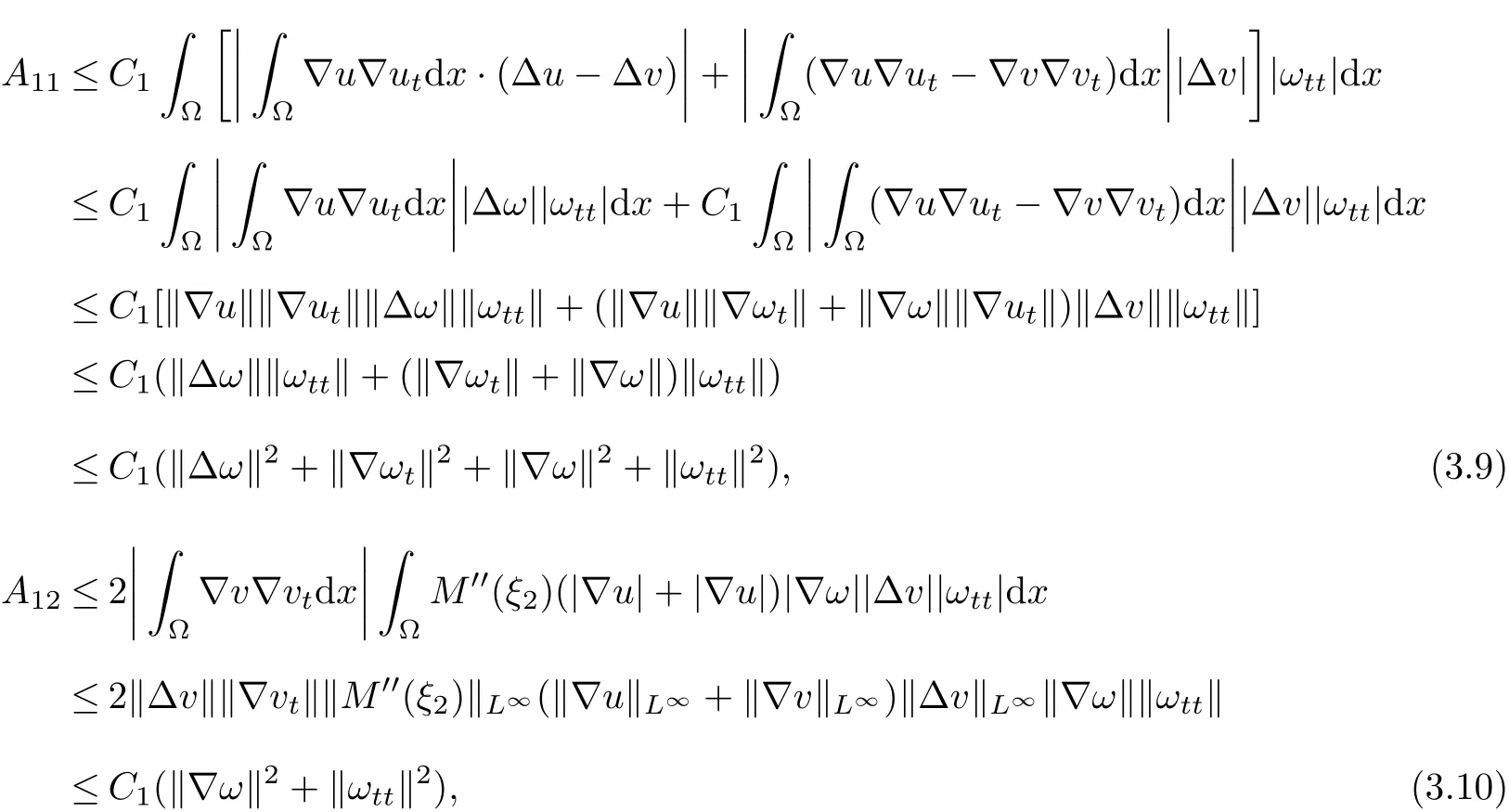
whereξ2=(1−θ1)‖▽u‖2+θ1‖▽v‖2andθ1∈(0,1).

Similarly,

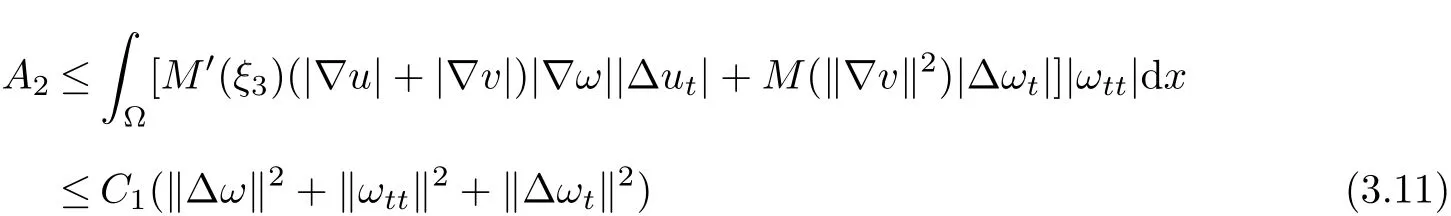
withξ3=(1−θ2)‖▽u‖2+θ2‖▽v‖2andθ2∈(0,1).

Combining(3.6)～(3.11),we obtain

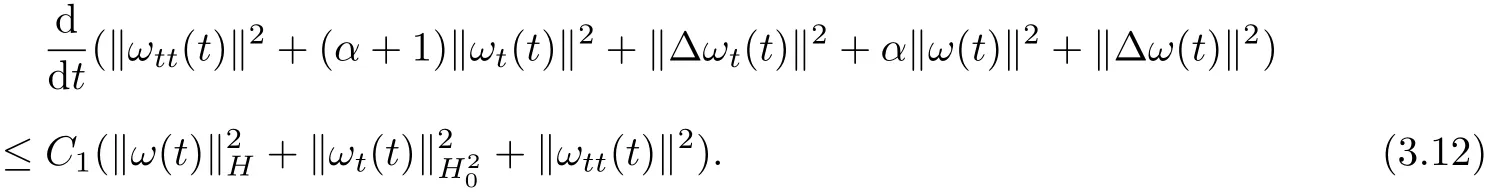
Now we define

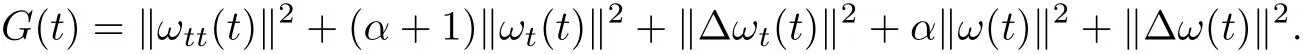
Then we can easily know that G(t)is equivalent to

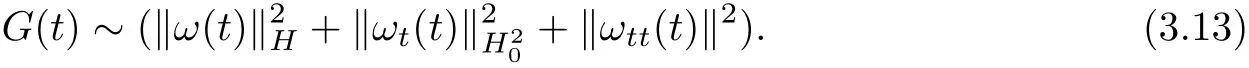
It follows from(3.12)～(3.13)that

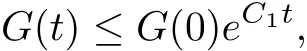
which,along with(3.13),gives

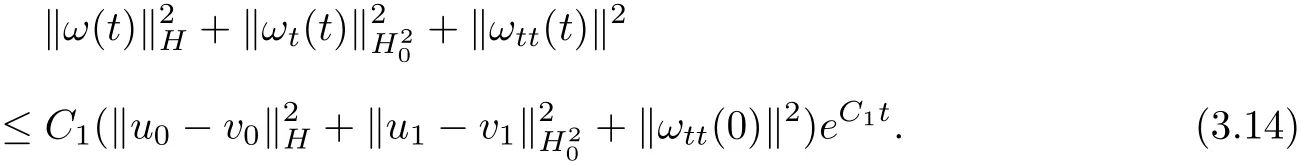
From(3.1),we can derive

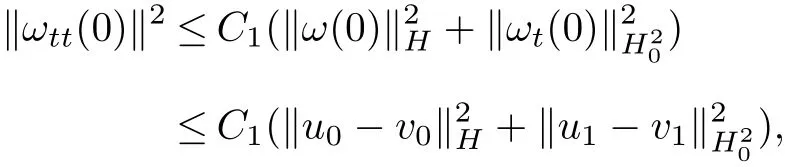
which,combined with(3.14),yields

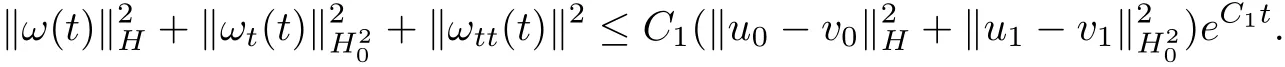
This shows that the solution of problem(1.1)～(1.3)depend continuously on the initial data.

In what follows,we shall show the uniform decay of energy defined in(2.4).

Multiplying(1.1)by utand integrating the resulting equation overΩ,we get

Let us define the functional

For everyε＞0,we define the perturbed modified energy by

Firstly,we claim that forε＞0 suffi ciently small

Indeed,by Young’s inequality and Poincar´e’s inequality,we get

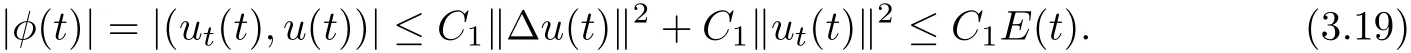
Then we have

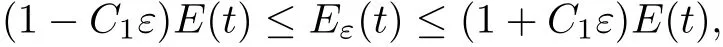
which,takingε＞0 smallenough,gives(3.18).

On the other hand,by(2.4),we have

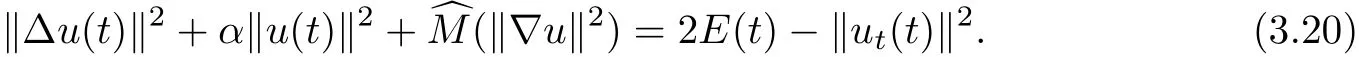
Using(1.1),integration by parts and Young’s inequality,we see that for anyδ＞0,

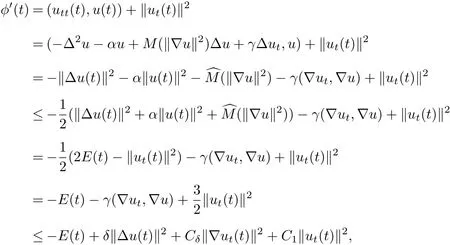
which,noting that‖Δu(t)‖2≤C1E(t)and takingδ＞0 small enough,implies

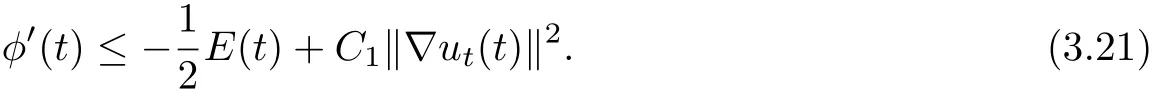
It follows from(3.15),(3.17)～(3.18)and(3.21)that

Takingε＞0 so smallthatγ−C1ε≥0 and using(3.18),we shallsee below,

and

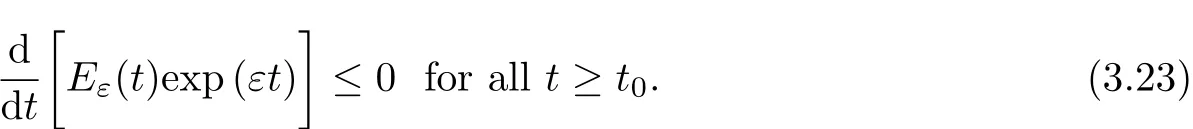
Integrating(3.23)and using inequality(3.18),we obtain

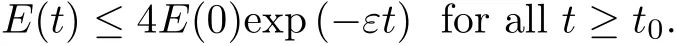
This concludes the proof of Theorem 1.

[1]WOINOWSKY-KRIEGER S.The eff ect of axial force on the vibration of hinged hars[J].Journal of Applied Mechanics,1950,17:35-36.

[2]BALL J M.Stability theory for an extensible beam[J].Journalof Differential Equations,1973,14:399-418.

[3]BALL J M.Initial-boundary value problems for an extensible beam[J].J Math Anal Appl,1973,42:61-90.

[4]DICKEY R W.Infi nite systems for nonlinear oscillation equations with linear damping[J].SIAM Journal on Applied Mathematics,1970,19:208-214.

[5]MEDEIROS L A.On a new class of nonlinear wave equations[J].J Math Anal Appl,1979,69:252-262.

[6]BRITO E H.Decay estimates for the generalized damped extensible string and beam equations[J].Nonlinear Analysis,1984,8(12):1489-1496.

[7]MA To-fu.Boundary stabilization for a non-linear beam on elastic bearings[J].Math Methods Appl Sci, 2001,24:583-594.

[8]OLIVEIRA M L,LIMA O A.Exponential decay of the solutions of the beam system[J].Nonlinear Analysis, 2000,42:1271-1291.

[9]RIVERA J E M,FATORI L H.Smoothing eff ect and propagations of singularities for viscoelastic plates[J]. J Math Anal Appl,1997,206(2):397-427.

[10]RIVERA J E M,LAPA E C,BARRETO R.Decay rates for viscoelastic plates with memory[J].Journal of Elasticity,1996,44(1):61-87.

[11]PATCHEU S K.On a global solution and asymptotic behavior for the generalized damped extensible beam equation[J].J.Diff erential Equations,1997,35:299-314.

[12]TUSNAL M.Semi-internal stabilization for a nonlinear Euler-Bernoulli equation[J].Math Methods Appl Sci,1996,19:897-907.

[13]CAVALCANTI M M,DOMINGOS CAVALCANTI V N,SORIANO J A.Global existence and asymptotic stability for the nonlinear and generalized damped extensible plate equation[J].Communications in Contemporary Mathematics,2004,6(5):705-731.

[14]MA To-fu,NARCISO V.Globalattractor for a modelofextensible beam with nonlinear damping and source terms[J].Nonlinear Analysis,2010,73:3402-3412.

[15]YANG Zi-jian.On an extensible beam equation with nonlinear damping and source terms[J].J Diff erential Equations,2013,254:3903-3927.

[16]VASCONCELLOS C F,TEIXEIRA L M.Existence,uniqueness and stabilization for a nonlinear plate system with nonlinear damping[J].Ann de la Fac des Sci de Toulouse,1999,VIII(1):173-193.

[17]PARK J Y,PARK S H.General decay for a nonlinear beam equation with weak dissipation[J].J Math Phys,2010,51:073508.

[18]CAVALCANTI MM,DOMINGOS CAVALCANTI V N,SORIANO J A.Globalexistence and uniform decay rates to the Kirchhoff-Carrier equation with nonlinear dissipation[J].Adv Diff erential Equations,2001,6(6): 85-116.

[19]ZUAZUA E.Stability and decay estimates for a class of nonlinear hyperbolic problems[J].Asymptotic Anal, 1988,1:161-185.

《数学季刊》征稿简则

一、办刊宗旨：

《数学季刊》由著名数学家陈景润先生于1986年创刊，创刊为中文版，现为英文版。是我国数学界委托河南大学承办，以刊登数学学科中具有创造性、代表学科水平的科研成果为主的综合性学术刊物。

二、来稿要求：

1.来稿正文用英文规范书写，要求语法正确，表达方式规范，并附中文题目、摘要、关键词、作者姓名、作者单位。

2.字数限制：论文限制在10个印刷页以内，文前摘要不超过6个印刷行，关键词1—7个。

3.在来稿的首页末注明作者简介，格式如下：姓名 （出生年—），性别 （民族——汉族可省略），籍贯，职称，学位，简历及研究方向 （任选）。获得基金资助产出的文章在首页末应注明基金项目名称，并在圆括号内注明其项目编号。

4.电子稿（Latex、PDF、Word）均可。

6.参考文献等其他格式要求请参阅已出版的数学季刊。

7.来稿请用E-mail发至本刊，本刊E-mail：sxjk＠henu.edu.cn；sxij＠henu.edu.cn

三、出版周期：

1.本刊从2011年开始不再收取任何费用，作者免费发表论文。

2.从收到稿件之日起，6个月内通知作者是否录用。

3.稿件一经录用，将在一年半时间内出版。

欢迎广大数学工作者踊跃投稿，我们将真诚为您服务！

tion:35L25,35L57

1002–0462(2014)01–0151–08

Chin.Quart.J.of Math. 2014,29(1):151—158

date:2013-06-15

Supported by the NNSF of China(11271066,11326158);Supported by the grant of Shanghai Education Commission(13ZZ048);Supported by the Doctoral Innovational Fund of Donghua University(BC201138)

Biography:FENG Bao-wei(1985-),male,native of Shangqiu,Henan,a Ph.D.candidate of Donghua University,engages in nonlinear evolution equations and infinite-dimensional dynamical systems.

CLC number:O175.29 Document code:A