Existence of Positive Solutions for Systems of Second-order Nonlinear Singular Diff erential Equations with Integral Boundary Conditions on Infi nite Interval

LI Yao-hong

(School of Mathematics and Statistics,Suzhou University,Suzhou 234000,China)

Existence of Positive Solutions for Systems of Second-order Nonlinear Singular Diff erential Equations with Integral Boundary Conditions on Infi nite Interval

LI Yao-hong

(School of Mathematics and Statistics,Suzhou University,Suzhou 234000,China)

By using cone theory and the M¨onch fixed theorem combined with a monotone iterative technique,we investigate the existence of positive solutions for systems of secondorder nonlinear singular diff erential equations with integral boundary conditions on infi nite interval and establish the existence theorem of positive solutions and iterative sequence for approximating the positive solutions.The results in this paper improve some known results.

boundary value problems;positive solutions;integralboundary conditions;the M¨onch fixed point theorem

§1. Introduction

Consider the following nonlinear singular boundary value problems for systems with integral boundary conditions on infinite interval in Banach spaces

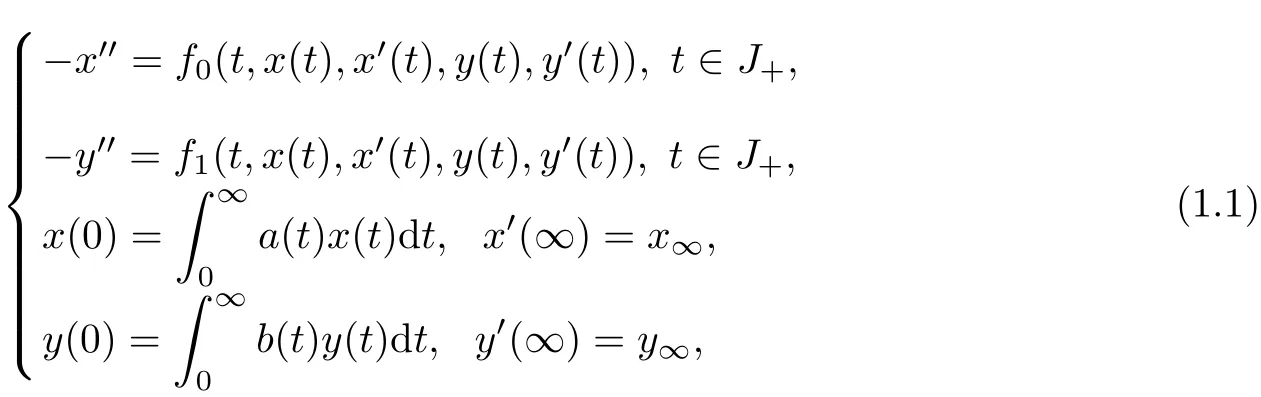
where J=[0,+∞),J+=(0,+∞),f0,f1may be singular at t=0,x,y=θand/or x′,y′=θ. θis the zero element of Banach spaces,a(t),b(t)∈L[0,∞)with

The theory of boundary value problems with integral boundary conditions for ordinary differentialequations arises naturally in diff erent fi eld ofapplied mathematics and physics thermal such as heat conditions,chemicalengineering,underground water flow.Such problems include two,three and multi-point boundary value problems as specialcases and attracted much attention(see[1-5]and the references therein).In particular,Zhang[1]investigated the existence of positive solutions for the following multi-point boundary value problems in a Banach space E

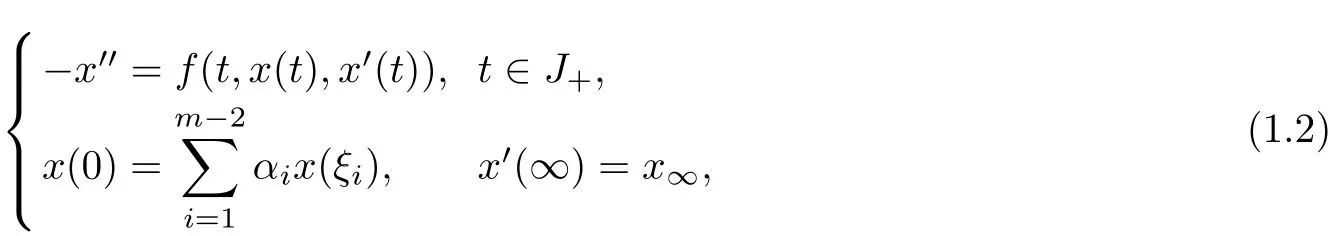
where J=[0,+∞),J+=(0,+∞),αi∈(0,+∞)with 0＜ξ1＜ξ2＜···＜ξm−2＜+∞,0＜.By using different methods,Li[2],Li[3],Chen[4]and Sun[5]improved the above results in different angles.

It seems that there are few results available for systems ofsecond-order differentialequations with integral boundary conditions on infinite interval.In this paper,we shall use cone theory and the M¨onch fixed theorem combined with a monotone iterative technique to investigate BVP(1.1).The existence theorem ofpositive solutions and iterative sequence for approximating the positive solutions are obtained.The results in this paper improve some known results.

§2.Preliminaries and Several Lemmas

Let

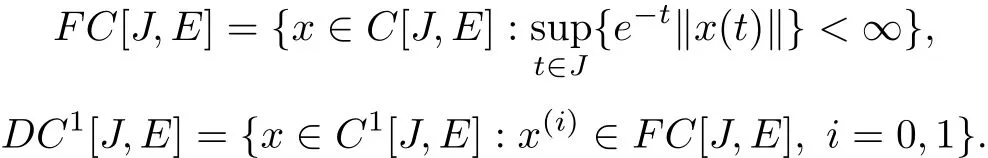
Obviously,F C[J,E],D C1[J,E]are two Banach spaces with normand‖x‖D=max{‖x‖B,‖x′‖B}.Let X=D C1[J,E]×D C1[J,E]with norm

Then(X,‖·,·‖X)is also a Banach space.This is the basic space using in this paper.

Let P be a normal cone in E with normal constant.P+=P{θ}.So,x∈P+if and only if x＞θ.For details on cone theory,see[6].In what follows,we always assume x∞＞ x∗,y∞＞ y∗,x∗,y∗∈P+,P0λ={x∈P:x≥ λx∗},P1λ={y∈P:y≥ λy∗} for anyλ＞0.Obvious,P0λ,P1λ⊂P+.Whenλ=1,we write P0=P01={x∈P:x≥x∗},P1=P11={y∈P:y≥y∗}.Let P(F)={x∈F C[J,E]:x≥θ,∀t∈J},P(D)={x∈D C1[J,E]:x(t)≥θ,x′(t)≥θ,∀t∈J}.It is clear,P(F),P(D)are two cones in F C[J,E]and D C1[J,E].A map(x,y)∈D C1[J,E]∩C2[J+,E]×D C1[J,E]∩C2[J+,E]is called a positive solution of BVP(1.1)if(x,y)∈P(D)×P(D)and(x,y)satisfies BVP(1.1).

Letα,αB,αD,αXdenotes the Kuratowski measure of non-compactness in E,F C[J,E], D C1[J,E]and X.Let L[J+,J]be all lebesgue measurable functions from J+to J.Denote

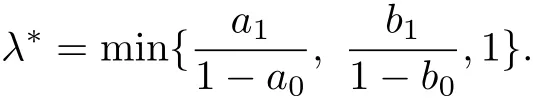
Let us list some conditions for convenience

(H1)fi∈C[J+×P0λ×P0λ×P1λ×P1λ,P]for anyλ＞0 and there exist ai(t),bi(t),ci(t)∈L[J+,J]and hi∈C[J+×J+×J+×J+,J].For any xi∈P0λ∗,yi∈P1λ∗,i=0,1,such that

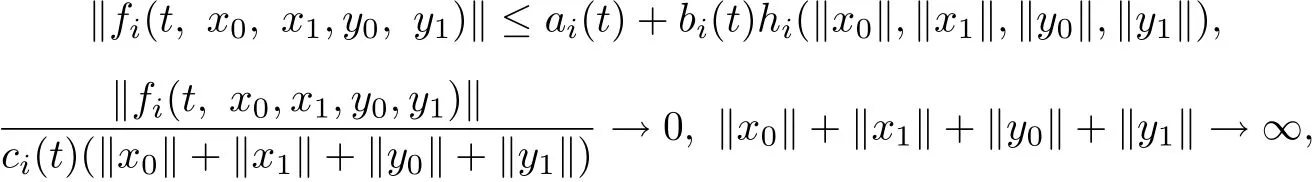
uniformly for t∈J+and

(H2)For any t∈J+,R＞0 and countable set0,1),there exist pij(t),qij(t)∈L[J+,J](i,j=0,1),such that

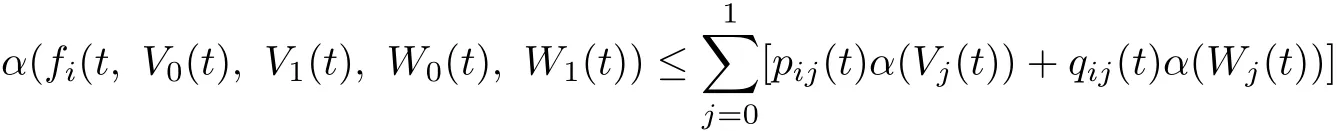
with

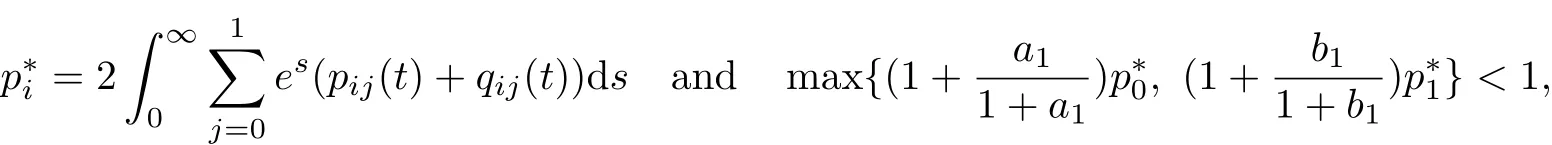
(H3)For anyimply

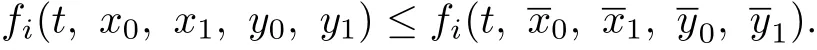
In what follows,we write Q1={x∈D C1[J,P]:x(i)≥ λ∗x∗,∀t∈J,i=0,1}and Q2={y∈D C1[J,P]:y(i)≥λ∗y∗,∀t∈J,i=0,1}and Q=Q1×Q2.Obviously,Q1,Q2,Q are closed convex sets in D C1[J,E]and X.We shall reduce BVP(1.1)to a system of integral equation in E.we first consider operator A defined by

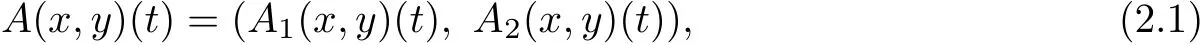
where

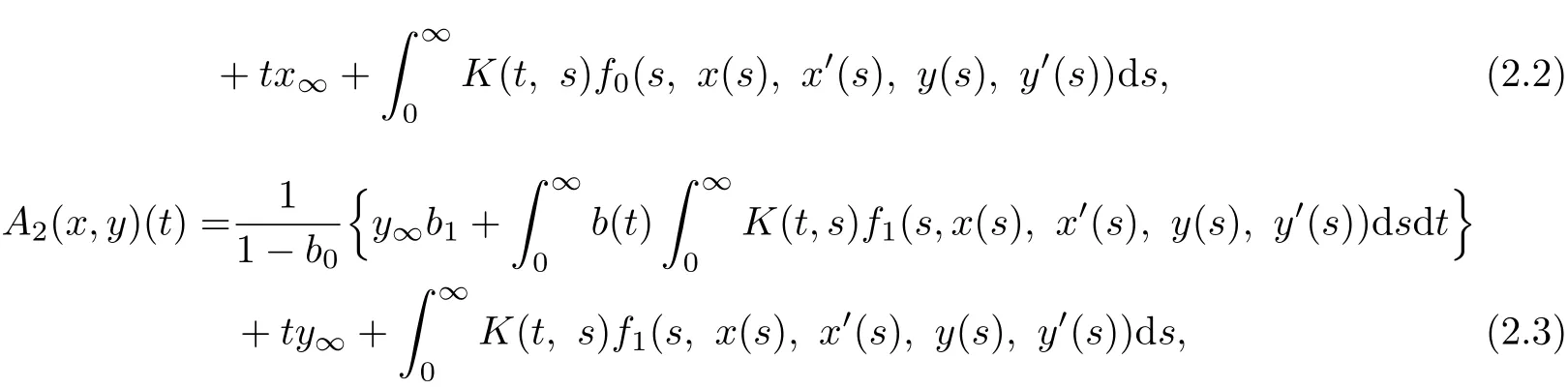
where

Lemma 2.1 Ifcondition(H1)is satisfied,then operator A defined by(2.1)is a continuous operator from Q into Q.

Proof Let

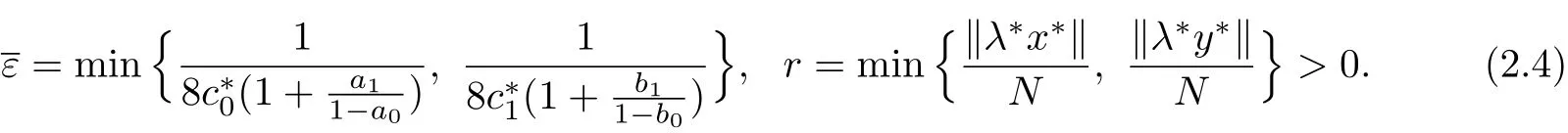
By(H1),there exists R0＞r,for any t∈J+,xi∈P0λ∗,yi∈P1λ∗,i=0,1,such that

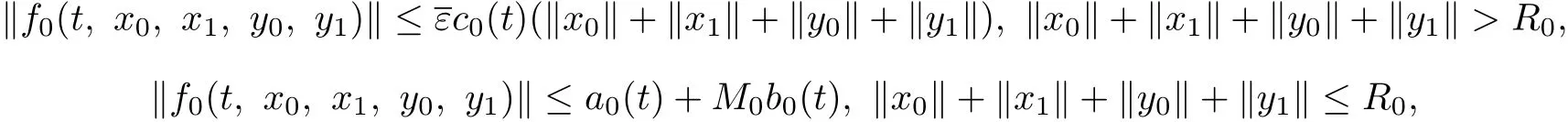
where M0=max{h0(u0,u1,v0,v1):r≤ui,vi≤R0,i=0,1}.Hence

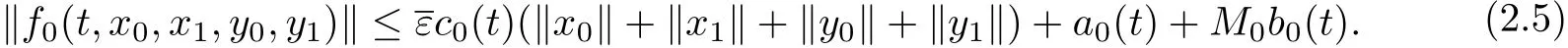
Let(x,y)∈Q,by(2.5),we have

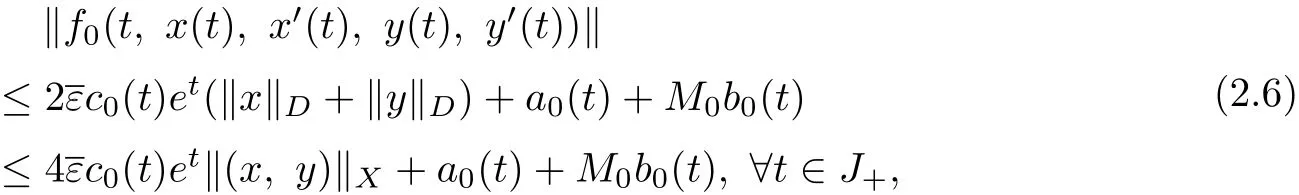
which together with condition(H1)implies the convergence of the infinite integral

Thus,by(H1),(2.2)and(2.7),we get

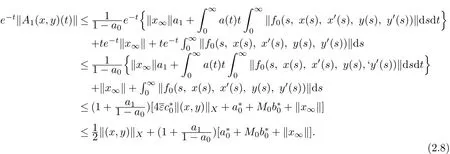
Diff erentiating(2.2),similar to(2.8),we get

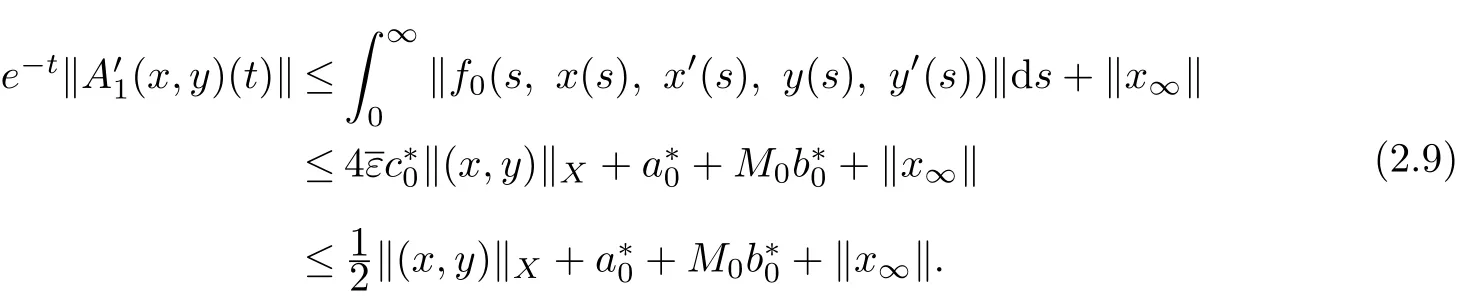
By(2.8)and(2.9),we can obtain that

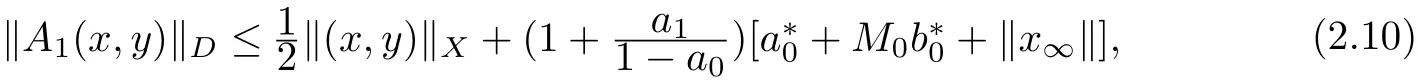
so,A1(x,y)(t)∈D C1[J,E].On the other hand,by(2.2),it can be easily seen that

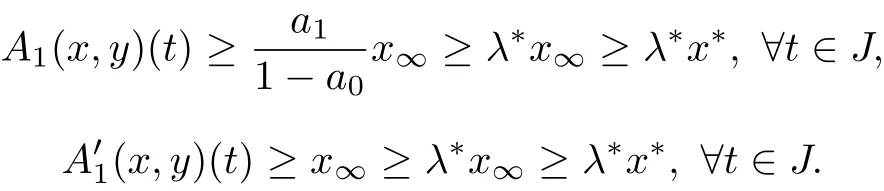
So,A1(x,y)(t)∈Q1.In the same way,we can easily get that

where M1=max{h1(u0,u1,v0,v1):r≤ui,vi≤R0,i=0,1}.So,A2(x,y)(t)∈Q2.Thus,A maps Q into Q and we get

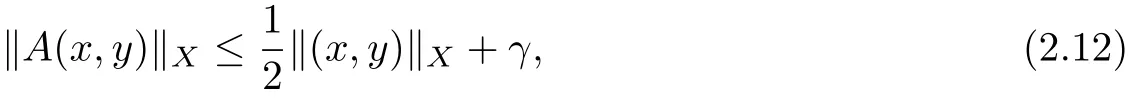
where

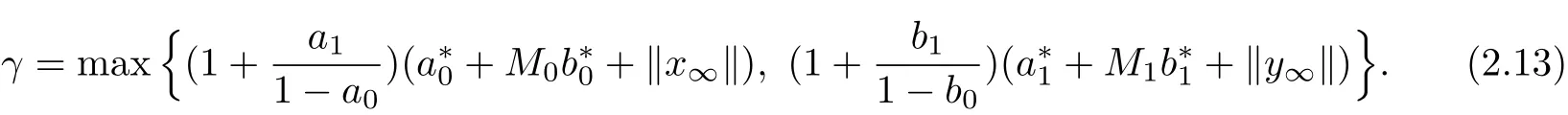
Finally,we show that operator A is continuous.LetThen{(xm,ym)}is a bounded subset of Q.Thus,there exists r＞0 such that‖(xm,ym)‖X≤r for m≥1 and‖(x,y)‖X≤r.Similar to the proof of Lemma 2.1 in [3],it is easy to know that‖A1(xm,ym)−A1(x,y)‖D→0 as m→∞.By the same method, we have‖A2(xm,ym)−A2(x,y)‖D→0 as m→∞.Therefore,the continuity of A is proved.

Lemma 2.2 If condition(H1)is satisfied,then(x,y)∈Q∩(C2[J+,E]×C2[J+,E])is a solution of BVP(1.1)if and only if(x,y)∈Q is a fixed point of operator A.

Proof It is easy to know that(x,y)∈Q∩(C2[J+,E]×C2[J+,E])is a solution of BVP (1.1)if(x,y)∈Q is a solution of the follow integral equation

Multiply by a(t)and b(t)on both sides of the above,integrate over[0,∞)and use x(0)=by direct calculations,we can obtain that

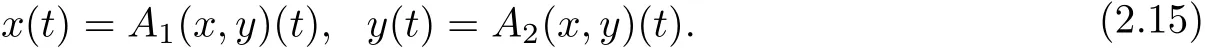
It follows from Lemma 2.1 that the integralare convergent.Thus,(x,y)is a fixed point of operator A.

Conversely,if(x,y)is a fixed point of operator A,direct differentiation gives the proof.

Lemma 2.3[7]Let H be a bounded set in D C1[J,E].Suppose that,H′(t)is equicontinuous on each Jk(k=0,1,2,···)and e−t‖x(i)(t)‖→ 0(i=0,1)as t→∞ uniformly x∈H. Then

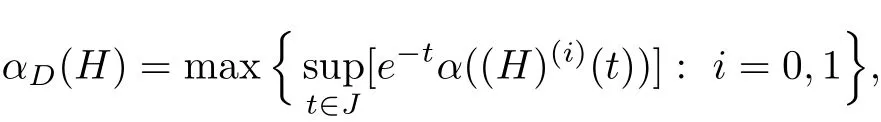
Lemma 2.4[6]Let H be a countable set of strongly measurable function x:J→E such that there exists M(t)∈L[J,R+]such that‖x(t)‖≤M(t)a.e.t∈J for all x∈H.Then α(H(t))∈L[J,R+]and

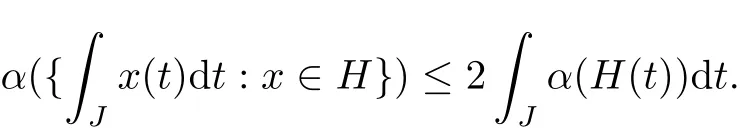
Lemma 2.5[8]Let D and F are bounded sets in E.Then

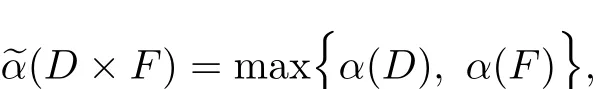
where~αandαdenote the kuratowskimeasure ofnoncompactness in E×E and E,respectively.

Lemma 2.6(M¨onch Fixed Point Theorem) Let K be a closed and convex subset of E and x∈K.Assume that the continuous operator F:K→K has the following property

C⊂K is countable and C⊂co({x}∪F(C))imply that C is relatively compact.

Then F has a fixed point in K.

Lemma 2.7 Ifcondition(H3)issatisfied.Then

It is easy to see that this lemma follows from(2.2),(2.3)and condition(H3).The proof is obvious.

§3.Main Results

Theorem 3.1 If conditions(H1)～(H3)are satisfied,then BVP(1.1)has a positive solutionsatisfying

Proof By Lemma 2.1,operator A defined by(2.1)is a continuous operator from Q into Q,and by Lemma 2.2,we need only to prove that A has a fixed point(x,y)in Q.Choose R＞2γ,whereγdefined by(2.13)and let Q∗={(x,y)∈Q:‖(x,y)‖X≤R}.Clearly,Q∗is a bounded closed convex set in space D C1[J,E]×D C1[J,E].It is easy to know that Q∗is not empty since(λ∗etx∞,λ∗ety∞)∈Q∗.It follows from(2.12)that(x,y)∈Q∗implies A(x,y)∈Q∗,that is,A:Q∗→Q∗.Now,we are in position to show that A(Q∗)is relatively compact.Let V={(xm,ym):m=1,2,···}⊂Q∗satisfying V⊂{{(x0,y0)}∪(AV)}for some (x0,y0)∈Q∗.Then‖(xm,ym)‖X≤R(m=1,2,3,···).By(2.2),we have

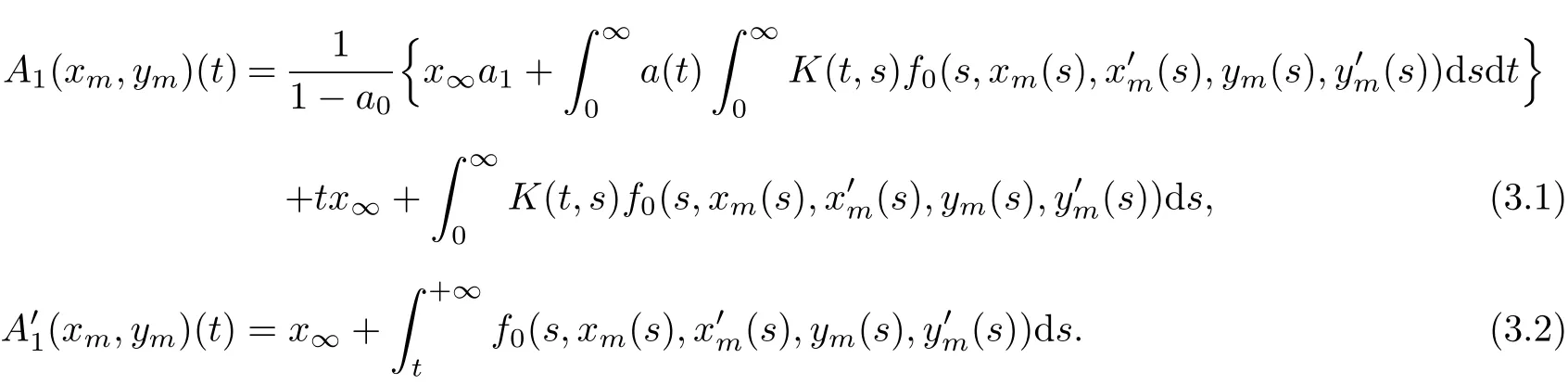
Hence,similar to the proof of Theorem 3.1 in[3],by Lemma 2.3,we have

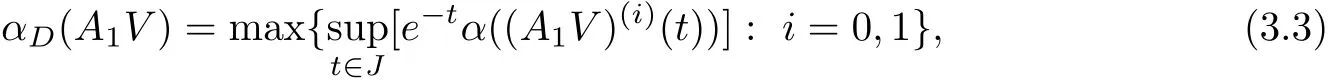
It follows from Lemma 2.1 that the infinite integral(2.7)is convergent uniformly for m= 1,2,3,···.So,for anyε＞0,we can choose a suffi ciently large T＞0 such that,for any m

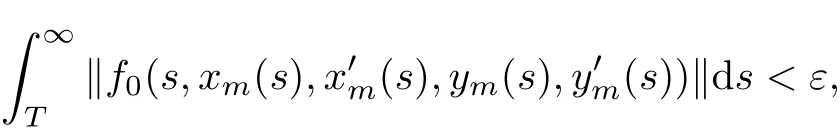
Then,by(2.2),(3.2),(H2),Lemma 2.4 and Lemma 2.5,we obtain

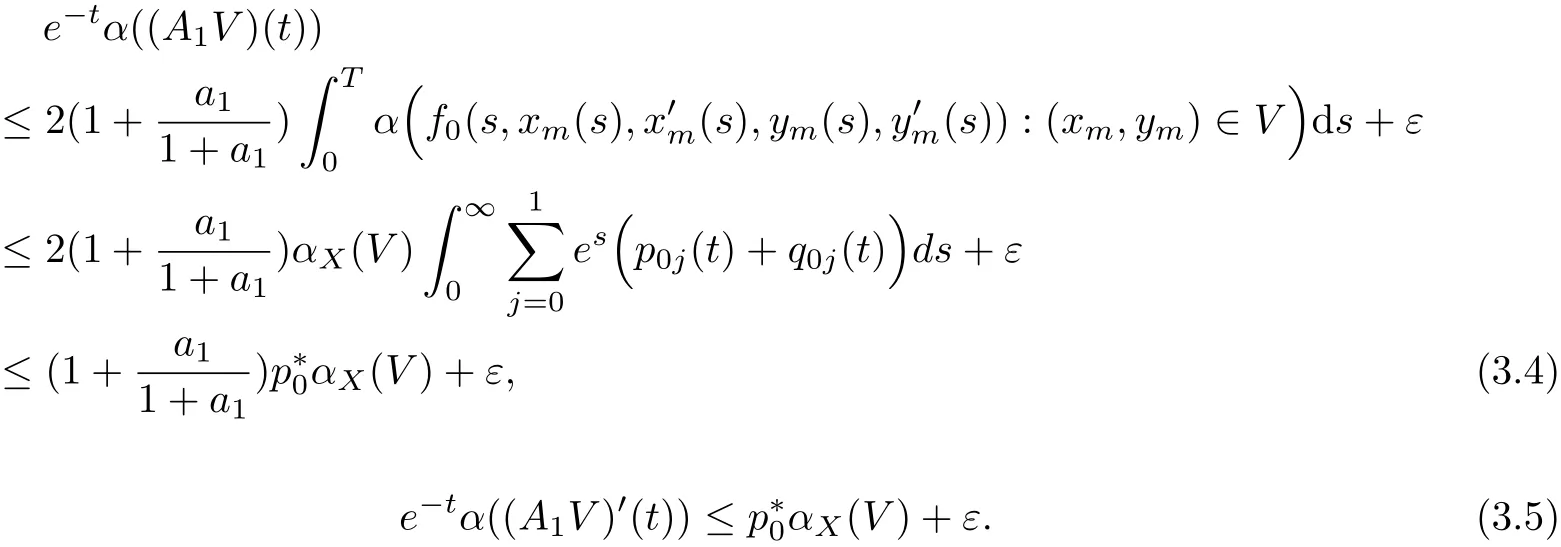
By(3.3)～(3.5)and noting thatε＞0 is arbitrary,we see that

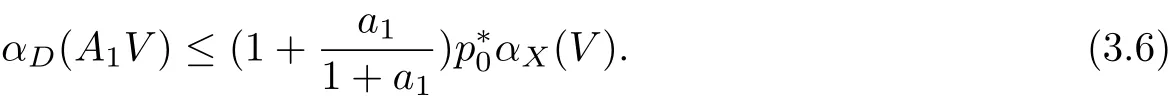
In the same way,we get

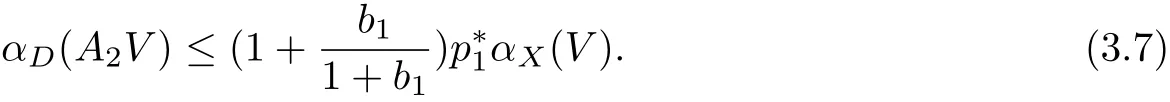
On the other hand,αX(V)≤αX{co({(x0,y0)}∪(AV))}=αX(AV).Then,(3.6),(3.7),(H2) and Lemma 2.5 implyαX(V)=0,that is,V is relatively compact in X.Hence,Lemma 2.6 implies that A has a fixed point(x,y)in Q∗.Thus,theorem 3.1 is proved.

Theorem 3.2 Let cone P is normaland conditions(H1)～(H3)are satisfied.Then BVP (1.1)has a positive solution(x,y)∈Q∩C2[J+,E]×C2[J+,E]which is minimal in the sense that u(i)(t)≥ x(i)(t),v(i)(t)≥ y(i)(t),t∈ J(i=0,1)for any positive solution(u,v)∈Q∩C2[J+,E]×C2[J+,E]of BVP(1.1).Moreover,‖(x,y)‖X≤2γ+‖(u0,v0)‖Xand there exists a monotone iterative sequence such thatas n→∞uniformly on J andas n→∞for any t∈J+,where

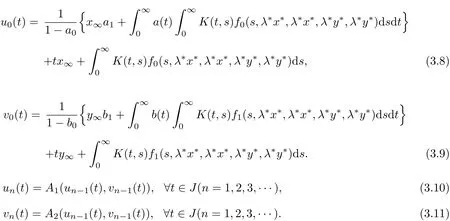
Proof From(3.8),we can see that(u0,v0)∈C[J,E]×C[J,E]and

By(3.8),(3.12)and(H1),we can know that u(i)0(t)≥x∞≥λ∗x∞≥λ∗x∗(i=0,1),

which imply that‖u0‖D＜∞.Similarly,we have‖v0‖D＜∞.Thus(u0,v0)∈X.It follows from(3.10),(3.11)and(2.1)that

By Lemma 2.1,we get(un,vn)∈Q and

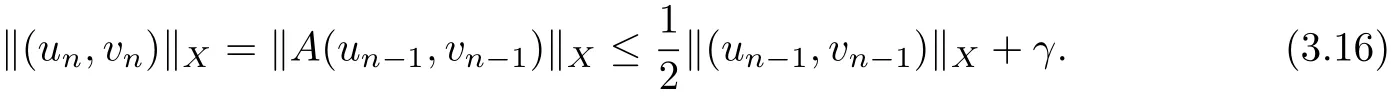
By(3.10),(3.11),(H3)and Lemma 2.7,we have

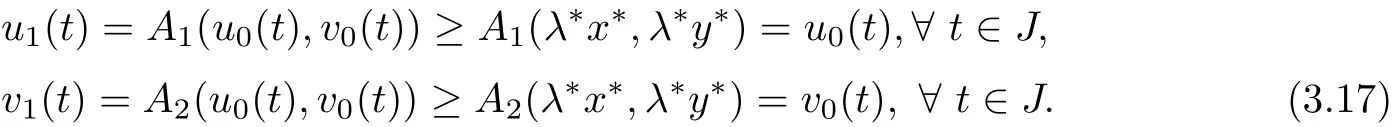
Similarly,it is easy to see that

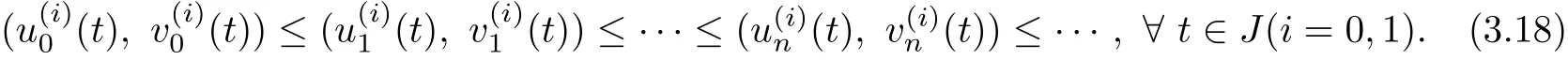
It follows from(3.16)and(2.12)that

Let K={(u,v)∈Q:‖(u,v)‖X≤2γ+‖(u0,v0)‖X}.Then K is a bounded closed convex set in space X and operator A maps K into K.Obviously,K is not empty since(u0,v0)∈K.Let W={(un,vn):n=0,1,2,···},AW={A(un,vn):n=0,1,2,···}. Obviously,W ∈K and W={(u0,u0)∪A(W)}.Similarly to the proof of Theorem 3.1, we can obtain thatαX(W)=0,that is,W is relatively compact in X.So,there exists a (x,y)∈X and a subsequence:i=0,1,j=1,2,3,···}⊂W such that:i=0,1,j=1,2,3,···}converges to(x(i)(t),y(i)(t))(i=0,1)uniformly on J.Since that P is normal and:n=1,2,3,···}is nondecreasing,it is easy to see that the entire sequence:i=0,1,n=1,2,3,···}converges to(x(i)(t),y(i)(t))(i=0,1)uniformly on J.Noticing the fact that(un(t),vn(t))∈K and K is closed convex set in space X,we have(x,y)∈K.It is clear that

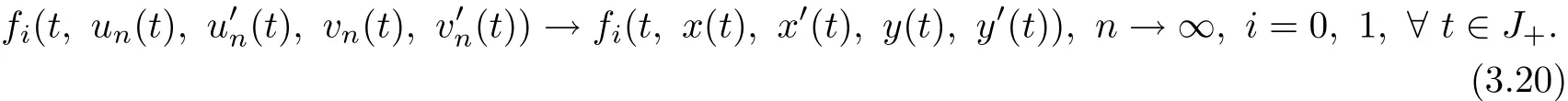
By(H1),(2.6)and(3.19),we have

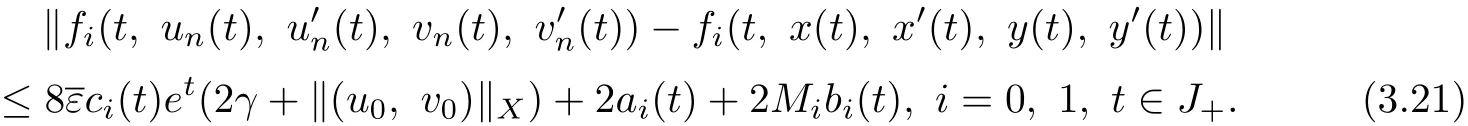
Noticing(3.20)～(3.21)and taking n→∞in(3.10)and(3.11),we obtain

(3.22)and Lemma 2.2 show that(x,y)∈K∩C2[J+,E]×C2[J+,E]and(x(t),y(t))is a positive solution of BVP(1.1).Differentiating(3.10)twice,we get

Hence,we have

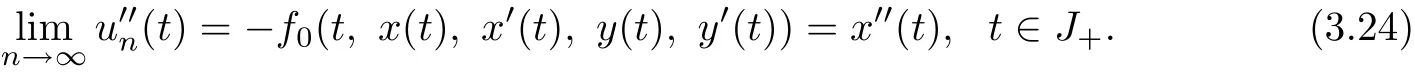
Similarly,one has

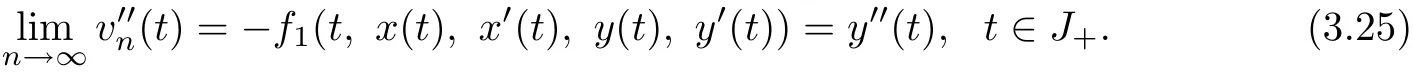
Let(p(t),q(t))be any positive solution of BVP(1.1).By Lemma 2.2,we have(p(t),q(t))∈Q,(p(t),q(t))=A(p,q)(t),∀t∈J.It is obvious that p(i)(t)≥λ∗x∗＞θ,q(i)(t)≥λ∗y∗＞θ,∀t∈J(i=0,1).So,by Lemma 2.7,we know thatJ(i=0,1).Suppose that ∀t∈J,n≥1(i=0,1),it follows from Lemma 2.7 that(t)),∀t∈J(i=0,1).That is

Taking limits in(3.26),we get p(i)(t)≥x(i)(t),q(i)(t)≥y(i)(t),∀t∈J(i=0,1).The proof is completed.

[1]ZHANG Xing-qiu.Existence of positive solutions for multi-point boundary value problems on infinite intervals in Banach spaces[J].Appl Math Comput,2008,206:935-941.

[2]LI Pei-luan,CHEN Hai-bo,ZHANG Qi.Multiple positive solutions of n-point boundary value problem on the half-line in Banach spaces[J].Commun Nonlinear Sci Numer Simulat,2009,(14):2909-2915.

[3]LI Yao-hong,ZHANG Xiao-yan.The existence of positive solutions for multipoint infi nite boundary value problems of second order nonlinear impulsive singular diff erential equations in Banach spaces[J].J Sys Sci and Math Scis,2011,31(7):859-871.

[4]CHEN Xu,ZHANG Xing-qiu.Existence of positive solutions for singular impulsive diff erential equations with integral boundary conditions on an infi nite interval in Banach spaces[J].Electronic Journal of Qualitative Theory of Diff erential Equations,2011,28(1):1-18.

[5]SUN Yan-mei.Existence of multiple positive solutions for second-order three-point boundary value problems on a half-line[J].Chin Quart J of Math,2012,27(1):24-28.

[6]GUO Da-jun,LAKSHMIKANTHAM V,LIU Xin-zhi.Nonlinear Integral Equations in Abstract Spaces[M]. Dordrecht:Kluwer Academic Publishers,1996.

[7]GUODa-jun.Existence ofsolutions for n-th-order impulsive integro-diff erentialequations in Banach spaces[J]. Nonlinear Anal,2001,47:741-752.

[8]GUO Da-jun,LAKSHMIKANTHAM V.Coupled fixed points of nonlinear operators with application[J]. Nonlinear Anal TMA,1987,11:623-632.

tion:34B16,34B18,34B40

1002–0462(2014)01–0055–10

Chin.Quart.J.of Math. 2014,29(1):55—64

date:2012-07-14

Supported by the NSF of Anhui Provincial Education Department(KJ2012A265, KJ2012B187)

Biography:LI Yao-hong(1978-),male,native of Wuhan,Hubei,an associate professor of Suzhou University, M.S.D.,engages in nonlinear functional analysis and application.

CLC number:O177.91 Document code:A