The Rank of Integral Circulant Graphs

ZHOU Hou-qing

(Department of Mathematics,Shaoyang University,Shaoyang 422004,China)

The Rank of Integral Circulant Graphs

ZHOU Hou-qing

(Department of Mathematics,Shaoyang University,Shaoyang 422004,China)

A graph is called an integral graph if it has an integral spectrum i.e.,all eigenvalues are integers.A graph is called circulant graph if it is Cayley graph on the circulant group,i.e.,its adjacency matrix is circulant.The rank of a graph is defined to be the rank of its adjacency matrix.This importance of the rank,due to applications in physics,chemistry and combinatorics.In this paper,using Ramanujan sums,we study the rank of integral circulant graphs and gave some simple computational formulas for the rank and provide an example which shows the formula is sharp.

integral circulant graph;eigenvalues;rank

§1. Introduction

Circulant graphs are Cayley graphs over a cyclic group.The interest of circulant graphs in graph theory and applications has grown during the last two decades,they appeared in coding theory,VLSI design,Ramsey theory and other areas.Recently there is vast research on the interconnection schemes based on circulant interconnection topology-circulant graphs represent an important class of interconnection networks in parallel and distributed computing(see[1-2]).Integral circulant graphs are also highly symmetric and have some remarkable properties between connecting graph theory and number theory.

In quantum communication scenario,circulant graphs is used in the problem of arranging N interacting qubits in a quantum spin network based on a circulant topology to obtain good communication between them.In general,quantum spin system can be defined as a collection of qubits on a graph,whose dynamics is governed by a suitable Hamiltonian,without external control on the system.Different classes of graphs were examined for the purpose of perfectlytransferring the states of the systems.Since circulant graphs are mirror symmetric,they represent good candidates for the property of periodicity and thus integrality[3],which further implies that integralcirculant graphs would be potentialcandidates for modeling the quantum spin networks that permit perfect state transfer[47].These properties are primarily related to the spectra of these graphs.Indeed,the eigenvalues of the graphs are indexed in palindromic order(λi=λn−i)and can be represented by Ramanujan’s sums.The rank of graph G is a basic graph parameter ofthe graph and has been used in graph theory and also in applications from computer science.Thus,it is natural and perhaps important to understand the behavior of this parameter with respect to a circulant graph.An interesting feature of this parameter is that,unlike most of graph parameters(such as the connectivity,the chromatic number etc), the rank is not monotone(adding edges may reduce the rank).So,it is not clear that one can define thresholds.Our study,however,willshed some light on this problem.

[8]studied some parameters of integral circulant graphs as the bounds for the number of vertices and the diameter,bipartiteness and perfect state transfer.[9]proposed a generalization of unitary Cayley graphs named gcd-graphs and proved that they have to be integral.We actually focus on characterization of the rank of integral circulant graphs ICGn(D).The outline of the paper is as follows:in Section 2 we will give definitions and preliminaries.Also in this section we will recall circulant graphs and some of their basic theory.In Section 3,we investigate the rank of an integralcirculant graphs ICGn(D).

§2. Preliminaries

All the graphs considered in this paper are finite,undirected and without multiple edges. Let us recall that for a positive integer n and subset S⊆{0,1,2,···,n−1},the circulant graph G(n,S)is the graph with n vertices,labeled with integers modulo n,such that each vertex i is adjacent to|S|other vertices{i+s(mod n)|s∈S}.

The set S is called a symbol of G(n,S).We assume that 0/∈S and s∈S if and only if n−s∈S and therefore the vertex i is adjacent to vertices i±s(mod n)for each s∈S.Let A be a circulant matrix.The entries a0,a1,···,an−1of the first row of the circulant matrix A generate the entries of the other rows by a cyclic shift(for more details see[10]).There is an explicit formula for the eigenvaluesλk,0≤k≤n−1,of a circulant matrix A.Define the polynomial Pn(z)by the entries of the first row of A,

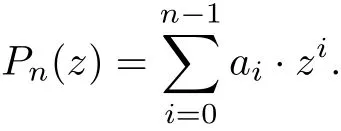
The eigenvalues of A are given by

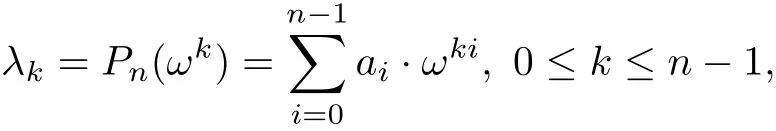
A graph is called an integral graph if it has an integral spectrum i.e.,all eigenvalues are integers.Two easy examples of integral graphs are the discrete graph on n vertices with spectrum(0,0,···,0)and the complete graph on n vertices with spectrum(n−1,−1(n−1)). So[11]has characterized circulant graphs with integral eigenvalues-integral circulant graphs. Let

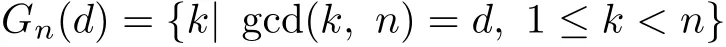
be the set of all positive integers less than n having the same greatest common divisor d with n.Let Dnbe the set of positive divisors d of n,withSo proved the following theorem [11].

Theorem A circulant graph G(n,S)is integral if and only if

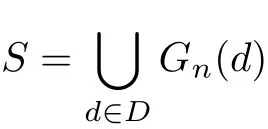
for some set of divisors D⊆Dn.

If D={d1,d2,···,dk},from Corollary 4.2 in[1],the graph IC Gn(D)is connected if and only if gcd(d1,d2,···,dk)=1.IC Gn(D)has k connected components if and only if gcd(d1,d2,···,dk)=k.The following proof will use this fact.

Ramanujan’s sum[12],usually denoted Rn(t),is a function of two positive integer variables n and t defined by the formula

φ(n),the Euler function,If the prime factorization of n is given byai＞0,i=1,2,···,t.Then

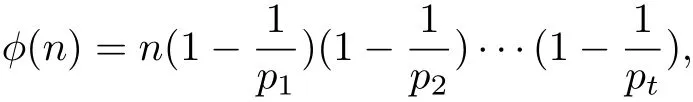
where p1＜p2＜···＜ptare prime numbers dividing n.

µ(n),the M¨obius function,is defined for allpositive integers n and has its values in−1,0,1 depending on the factorization of n into prime factors.It is defined as follows:

µ(n)=1 if n is a square-free positive integer with an even number of prime factors.µ(n)=−1 if n is a square-free positive integer with an odd number of prime factors.µ(n)=0 if n is not a square-free integer.Note that Rn(0)=|Gn(1)|=φ(n)and Rn(1)=µ(n).With the convention gcd(0,n)=n andφ(1)=1=µ(1).

In[9]it was proven that gcd-graphs(the same term as integralcirculant graphs)have integral spectrum,

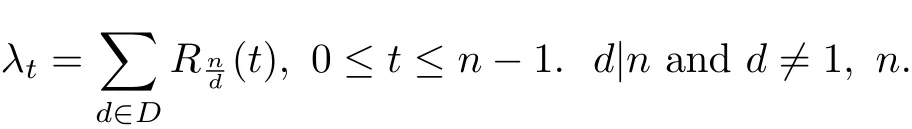
A graph is said to be singular if its adjacency matrix A is a singular matrix;then{v0: Av0=0}is the null-space of A denoted byε0(A).The nullity of G,denoted byη(G)is thedimension ofε0(A),which is the multiplicity of the zero eigenvalue of A,since A is symmetric. The rank of a graph G,denoted by rank(G),is the rank of its adjacency matrix A which is n(G)−η(G),where n(G)denotes the order of G.If a graph is not connected its rank is the sum of the rank of its connected components.This importance of the rank,due to applications in physics,chemistry and combinatorics,has spurred work in the determination of the rank for many types of graphs.

The rank have been studied by many scholars,previous work includes ranks of trees,grid graphs,Cartesian products[13]and circulants[1415];ranks of graphs after vertex addition[16]; ranks of graphs after edge insertion or deletion[17];ranks of line graphs[18]and ranks of graphs under unary operations[19].Here,we determine the ranks of integral circulant graphs.

The following claim holds

Claim 2.1[20]If A is an n×n matrix,then the rank of A plus the nullity of A is equal to n.

A scalarλis an eigenvalue of an n×n matrix A if there exists a nonzero vector x∈Rnsuch that Ax=λx or equivalently,(A−λI)x=0.If an eigenvalue is zero,then the nullspace is the set of solutions to Ax=0,so that the nullity of A gives the number of eigenvalues equal to zero.As a consequence of the above Claim 2.1,the rank of a matrix(it is diagonalizable)is equal to the difference of the dimension of the matrix and the number of eigenvalues equal to zero.

As example ofthe preceding Claim 2.1,we consider the complete graph Kn.Since spec(Kn)= (n−1,−1(n−1)),by above Claim 2.1,we have rank(Kn)=n.

The following lemmas will be crucial,found in[21].

Lemma 2.2 Let n=pkm,where p is a prime number,k＞1 and gcd(m,p)=1.If λiare eigenvalues of IC Gm({1})with multiplicity ti,then the eigenvalues of IC Gn({1,p})are−pk−2λi,(pk−pk−2)λiand 0 with multiplicity(p2−1)ti,tiand(pk−p2)m,respectively.

Lemma 2.3 Let n=pqm where p,q are distinct prime numbers and gcd(m,pq)=1.If λiare eigenvalues of IC Gm({1})with multiplicity ti,then the eigenvalues of IC Gn({p,q})are−2λi,(p−2)λi,(q−2)λiand(p+q−2)λiwith multiplicity(p−1)(q−1)ti,(q−1)ti,(p−1)tiand ti,respectively.

§3.Main Results

We turn our attention to the rank ofintegralcirculant graphs IC Gn(D).Note that arbitrary divisor d and 1≤i≤n−1,it holds

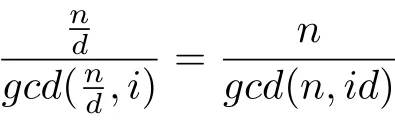
and

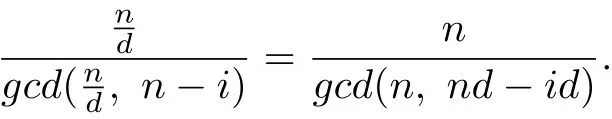
Since g cd(n,id)=gcd(n,nd−id),thus

for each 1≤i≤n−1.Therefore we have the following fact

Fact 3.1 Let IC Gn(D)be an arbitrary integral circulant graph.Then for each 1≤i≤n−1,the eigenvaluesλiandλn−iof IC Gn(D)are equal.

For i=0 we have

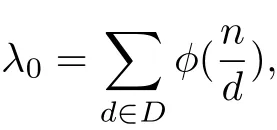
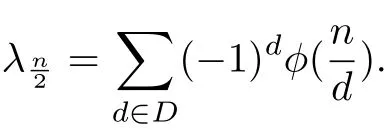
As we previously said,λt,the eigenvalues of integralcirculant graphs,

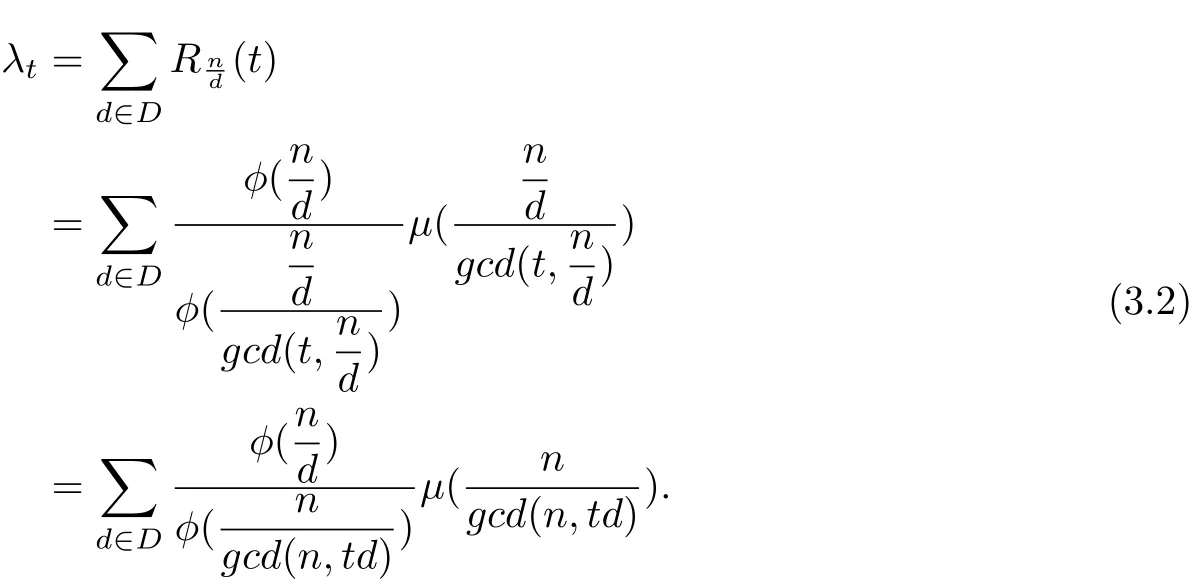
We are interested in determining the conditions that give zero eigenvalues for an integral circulant graph;conditions which will then determine the rank.

Using the fundamentaltheorem of arithmetic:Any integer greater than 1 is either a prime number,or can be written as a unique product of prime numbers(ignoring the order).

Now we prove the following theorem

Theorem 3.2 Let IC Gn({d})be an arbitrary integral circulant graph on n vertices,d denotes a divisor of n.Then the following equality holds

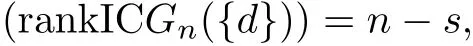
where s denotes the number of t(1≤t≤n)such that

Proof Without loss of generality,we may assume that

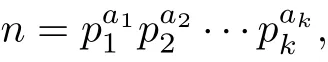
where p1,p2,···,pkare distinct primes,ai＞0,i=1,2,···,k.

For positive divisors d of n,let

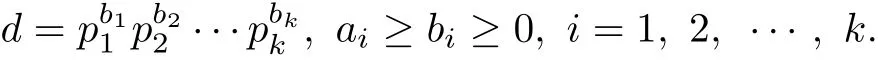
Then,we have

Thus,we obtain

Hence,we get

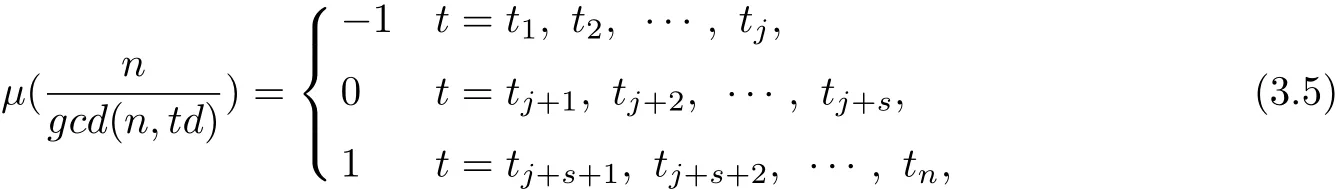
where all ti∈{1,2,···,n},ti/=tj.

Therefore,we have the following two cases

Then,we obtain

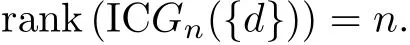
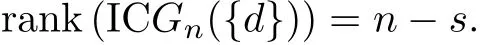
Example 3.3 Again,we illustrate this by examining the integralcirculant graph,IC G24(D), on 24 vertices.

Let d=3,the prime divisors of 24.Let D={3}⊆D24={1,2,3,4,6,8,12}.

Then,

Therefore,

Hence,we have

By(3.2),we have

That is,there are 18 zero eigenvalues of IC G24({3}).According to Theorem 3.2,we have

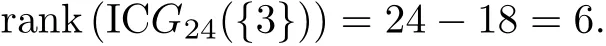
On the other hand,by a straightforward calculation,we obtain the following spectrum of IC G24({3})

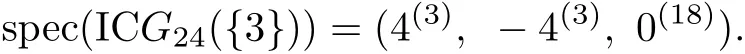
Thus,rank(IC G24({3}))=6.

Obviously,this formula for the rank of integral circulant graph is sharp.Now we turn our attention to two types of integral circulant graphs n=pkm,k＞1 and n=pqm,where (p,m)=1 and(pq,m)=1.

We have the following theorem

Theorem 3.4 Let n=pkm,k＞1.Then rank(IC Gn({1,p}))=p2m,where p,m are distinct prime numbers.

Proof Suppose n=pkm,k＞1,m is a prime number,by(3.2),the eigenvalues of the integralcirculant graph IC Gm({1})are

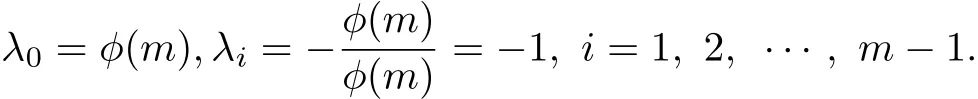
Using Lemma 2.2,we have the eigenvalues of IC Gn({1,p})

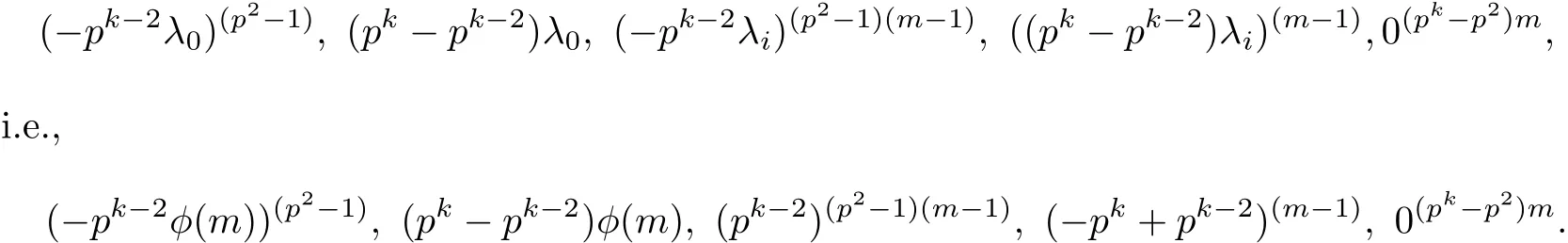
Thus,we have rank(IC Gn({1,p}))=p2m.

We see that there will not be any zero eigenvalues and by Claim 2.1,the next result easily follows.

Theorem 3.5 Let n=pqm,p,q,m are distinct prime numbers,then

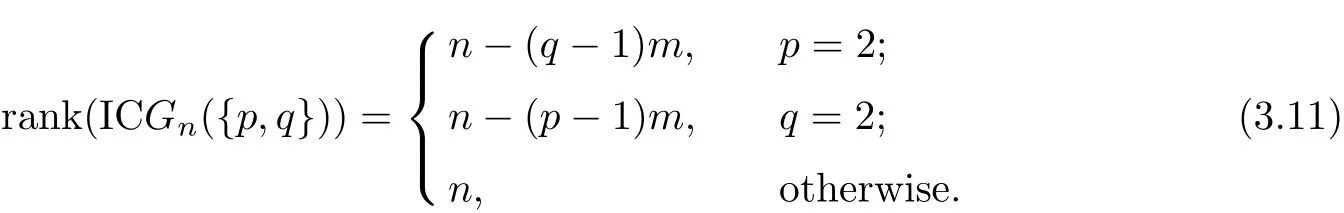
Proof Suppose n=pqm,p,q,m are distinct prime numbers and(pq,m)=1.Similarly, the eigenvalues of IC Gm({1})are

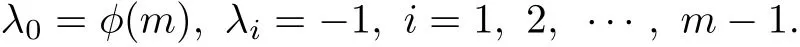
According to Lemma 2.3,we have,for IC Gn({p,q}),the following eigenvalues

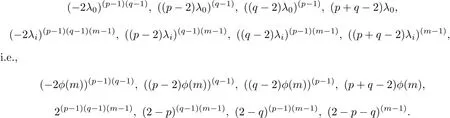
When p=2,p−2=0.Clearly,q/=2,there exist(q−1)m zero eigenvalues.Hence,we can determine the rank of IC Gn({p,q})=n−(q−1)m.

Similarly,when q=2,q−2=0,there are(p−1)m eigenvalues of 0,we obtain the rank of IC Gn({p,q})=n−(p−1)m.

Thus,we arrive at theorem.

Remark 3.6 In this work we studied the rank ofseveralcases ofintegralcirculant graphs. For circulant graphs and even more general graphs,we haven’t discussed yet their rank.The next possible step includes ranks ofcirculant graphs and generalgraphs,we hope allthe results willbe summarized and a relationship between a graph and its rank willbe found.

Acknowledgment The author is gratefulto anonymous referee for their usefulcomments and suggestions,which were helpful in improving the manuscript.

[1]HWANG F K.A survey on multi-loop networks[J].Theoretical Computer Science,2003,299(1):107-121.

[2]WEI Er-ling,HE Wei-li,LIU Yan-pei.The minimal cyele basis of circular graphs[J].Chinese Quarterly Journal of Mathematics,2007,22(1):7-11.

[3]CHRISTANDL M,DATTA N.Perfect transfer of arbitrary states in quantum spin networks[J].Physical Review A,2005,71:032312.

[4]AHMADIA,BELK R.On mixing in continuous time quantum walks on some circulant graphs[J].Quantum Information and Computation,2003,3(6):611–618.

[5]ANGELES-CANUL R,NORTON R M.Perfect state transfer,integral circulants and join of graphs[J]. Quantum Information and Computation,2010,10(3&4):325–342.

[6]ANGELES-CANUL R,NORTON R M.Quantum perfect state transfer on weighted join graphs[J].International Journal of Quantum Information,2009,7(8):1429–1445.

[7]GODSIL C.Periodic graphs[J].The Electronic Journal of Combinatorics,2011,18(1):50–65.

[8]SAXENA N,SEVERINI S,SHPARLINSKI I.Parameters of integralcirculant graphs and periodic quantum dynamics[J].International Journal of Quantum Information,2007,5(3):417–430.

[9]KLOTZ W,SANDER T.Some properties of unitary Cayley graphs[J].The Electronic Journal of Combinatorics,2007,14(1),#R45.

[10]DAVIS P J.Circulant Matrices[M].New York-Chichester-Brisbane:John Wiley and Sons,1979.

[11]WASIN SO.Note Integral circulant graphs[J].Discrete Mathematics,2005,306:153–158.

[12]RAMANUJAN.On certain trigonometrical sums and their applications in the theory of numbers[J].Transactions of the Cambridge Philosophical Society,1918,22:259–276.

[13]BEVIS J H,DOMKE G S,MILLER V A.Ranks of trees and grid graphs[J].Journal of Combinatorial Mathematics and Combinatorial Computing,1995,18:109–119.

[14]DAVIS G J,DOMKE G S.Three-circulant graphs[J].Journal of Combinatorial Mathematics and Combinatorial Computing,2002,40:133–142.

[15]DAVIS G J,DOMKE G S,GARNER C R.Ranks of four-circulant graphs[J].Ars Combinatoria,2002,65: 97–110.

[16]BEVIS J H,BLOUNT K K,DAVIS G J.The rank of a graph after vertex addition[J].Linear Algebra and Its Applications,1997,265:55–69.

[17]DAVIS G J.The rank of a graph after edge insertion or deletion[J].Congressus Numerantium,1998,133: 31–43.

[18]DAVIS GJ,DOMKE G S,GARNER CR.Ranks ofline graphs ofregular graphs[J].Journalof Combinatorial Mathematics and Combinatorial Computing,2004,49:113–128.

[19]GARNER C R,DAVIS G J,DOMKE G S.Ranks of regular graphs under certain unary operations[J].Ars Combinatoria,2005,74:3–24.

[20]LANCASTER P,TISMENETSKY M.The Theory of Matrices[M].San Diego:Academic Press,1985.

[21]MOLLAHAJIAGHAEI M.The eigenvalues and energy of integral circulant graphs[J].Transactions on Combinatorics,2012,1(3):47–56.

tion:05C50

1002–0462(2014)01–0116–9

Chin.Quart.J.of Math. 2014,29(1):116—124

date:2013-09-04

Supported by Hunan Provincial Natural Science Foundation(13JJ3118)

Biography:ZHOU Hou-qing(1963-),male,native of Shaoyang,Hunan,an associate professor of Shaoyang University,engages in graph theory and its applications.

CLC number:O157.5 Document code:A