The Method of Solutions for some Kinds of Singular Integral Equations of Convolution Type with Both Refl ection and Translation Shift

LI Ping-run

(School of Mathematical Sciences,Qufu Normal University,Qufu 273165,China)

The Method of Solutions for some Kinds of Singular Integral Equations of Convolution Type with Both Refl ection and Translation Shift

LI Ping-run

(School of Mathematical Sciences,Qufu Normal University,Qufu 273165,China)

In this paper,some kinds of singular integral equations of convolution type with reflection and translation shift are discussed and they are turned into Riemann boundary value problems with both discontinuous coeffi cients and reflection by using the Fourier transform.In spite of the classical method for solution,we are to give another method,therefore the general solution and condition of solvability are obtained in class{0}.

singular integralequation;convolution type;Riemann boundary value problem; reflection;translation shift

§0. Introduction

In 1977,Gakhov F D and Chersky U I proposed and studied some classes ofsingular integral equations with convolution kernels,and established the existence of general solutions in class {{0}}[1].In 1978,Litvinchuk G S studied the method of solution for the singular integral equations with translation as well as their boundary value problems[2].In this paper,some classes of singular integral equations of convolution type with both reflection and translation shifts are proposed and studied.These equations are transformed into Riemann boundary value problem with both reflection and discontinuous coeffi cients by using the Fourier transform,and then into the Riemann boundary value problem with functionalgroup,thus our paper promotes the results of the above-mentioned literature[12].

§1.Defi nition and Lemma

Defi nition 1.1 The Fourier transform of a functionω(t)will be denoted byΩ(s)

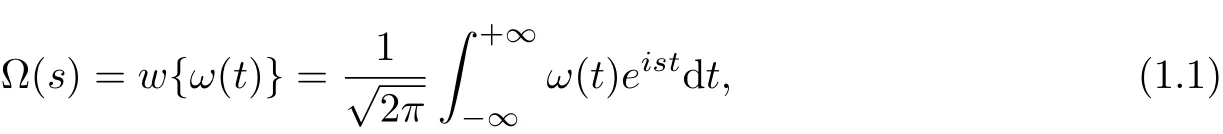
where the integral(1.1)exists.

Defi nition 1.2 The inverse Fourier transform of a functionω(t)is defined as follows

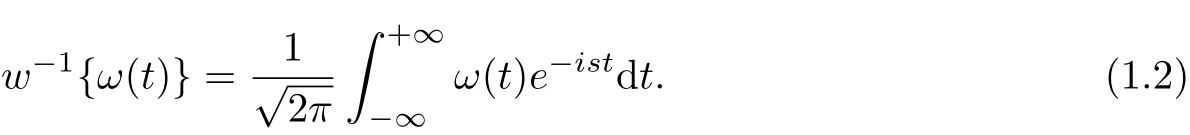
Then we have w{ω(−t)}=w−1{ω(t)}=Ω(−s).

Defi nition 1.3 A functionΩ(s)belongs to{{0}},if the following condition are fulfilled(for notation,cf[3]or[4]).

Defi nition 1.4 A function f(t)∈0,ifits Fourier transformω(t)eistd t belongs to class{{0}}.

Defi nition 1.5 The Fourier transform of the convolution ofω(t)and k(t)

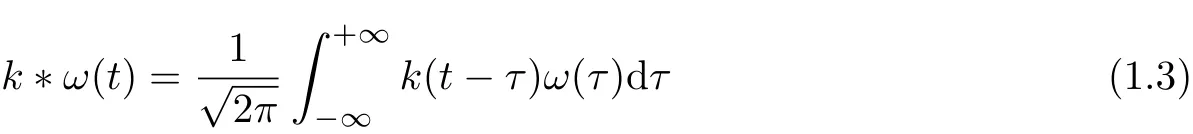
is w{k∗ω(t)}=wk·wω=K(s)Ω(s).

Defi nition 1.6 The operators N and T are defined as follows

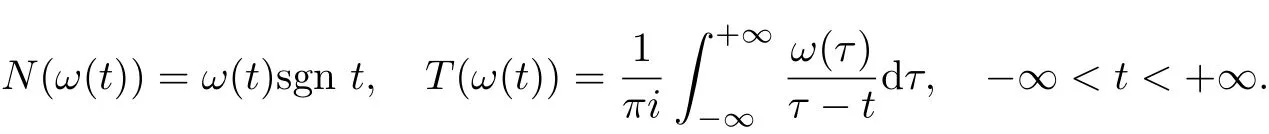
Lemma 1.1 When applying to functions in{0},we have w(Tω(t))=−NΩ(s).

Proof Owing to

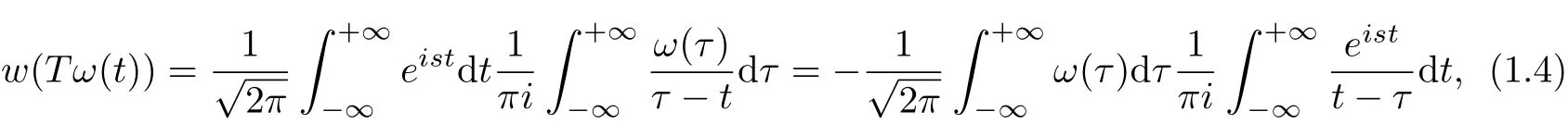
by using extended Residue theorem[5],we get

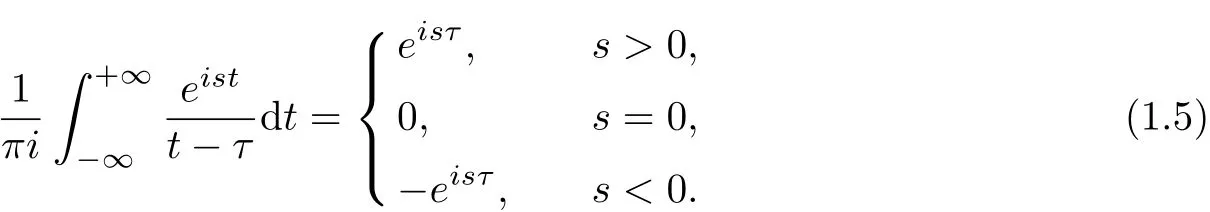
Putting(1.5)into(1.4),we have

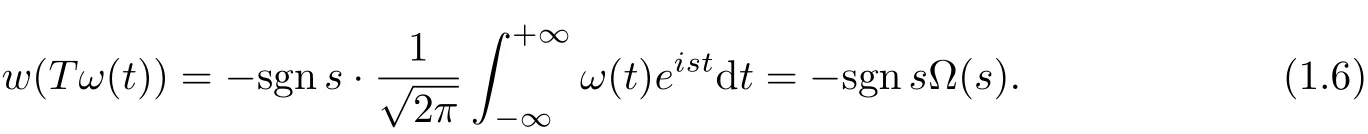
Evidently,w[T(ω(−t))]=−Ω(−s)sgn s.

Lemma 1.2 Ifω(t)∈{0}andΩ(0)=0,then Tω(t)belongs to the same class{0}.

Proof By supposition,Ω(s)∈{{0}}.From Lemma 1.1,w(Tω(t))=−SΩ(s).Noting thatΩ(∞)=Ω(0)=0,we know w(Tω(t))∈{{0}}.Therefore Tω(t)∈{0}.

§2.A Typical but Simple Equation of Convolution Type with Refl ectionω(t)andω(−t)

Let us solve the following equation

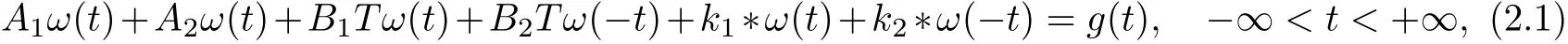
where Aj,Bjare constants with Bjnot all equal to zero simultaneously.k1(t),k2(t)and g(t)are the given functions,ω(t)is the unknown function,and kj(t),g(t)∈{0}.Obviously,Ω(s),Kj(s)and G(s)allbelong to class{{0}}.Taking Fourier transforms in both sides of(2.1), then(2.1)is reduced to

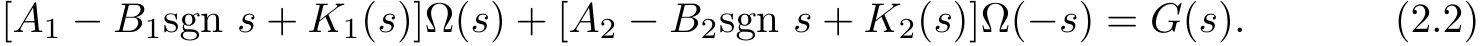
Owing toω(t)∈{0},Tω(t)∈{0},then we getΩ(0)=0,so the necessary condition of the existence of solution for the equation(2.1)is G(0)=0.Restricting ourselves to the normal type,i.e.,,where

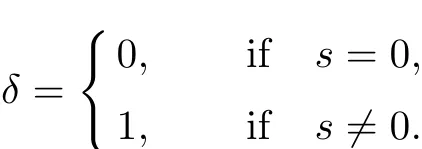
Replacing s by−s in(2.2),we obtain

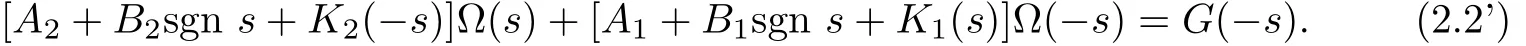
DenoteΔj(±s)=Aj∓Bjsgn s+Kj(±s)(j=1,2).Then,we may write(2.2),(2.2’)as

where

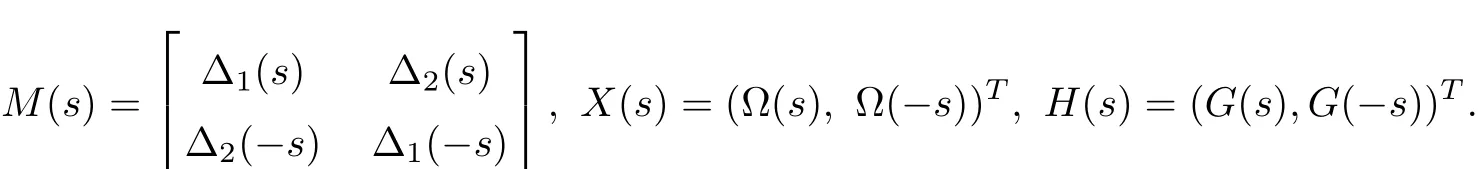
Next we would solve equations(2.3)with unknown functionsΩ(s)andΩ(−s)and denote

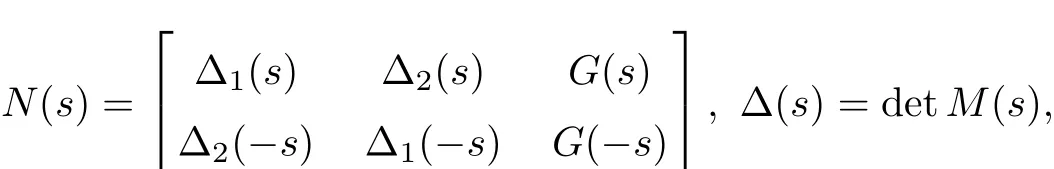
then

Since Kj(±s)∈{{0}},then Kj(±s)→0,Δ(s)→/=0 when s→∞. Thus there exists an X(X＞0)such thatΔ(s)/=0,when|s|＞X.Therefore the system of equation(2.3)has only solutionΩ(s)

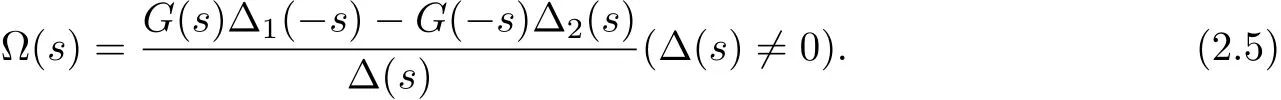
When|s|≤X,we consider the following cases

1) IfΔ(s)/=0(−∞ ＜ s＜ +∞),then the system of equation(2.3)has only solution M−1(s)H(s).

2) Ifthere exist s1,s2,···,sn∈[−X,X]such thatΔ(si)=0 and∂M(si)=∂N(si)(1≤i≤n),then the system of equations(2.3)has infinite solutions(Ω(s),Ω(−s)),where∂M is rank of matrix M.

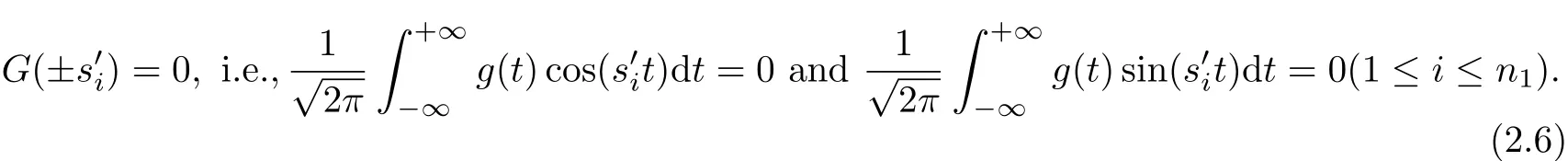
For homogeneous case,i.e.,g(t)≡0,the equation(2.1)has linearity independent solutions eis1t,eis2t,···,eisnt.Thus,we get

Theorem 1 Under the condition G(0)=0,

(1)IfΔ(s)/=0(−∞＜s＜+∞),then the equation(2.1)has a unique solution in class{0}, which is˜ω(t)=w−1{Ω(s)},whereΩ(s)is given by(2.5).

(2)IfΔ(s)=0 and∂M(s)=∂N(s)for s=s1,s2,···,sn,then the equation(2.1)has infinite solutionsω(t)=w−1{Ω(s)}.

(3)IfΔ(s)=0 and∂M(s)/=∂N(s)forthen the conditionsofsolvability(2.6)must be augmented.Therefore,the generalsolution of(2.1)arewhere ajare constants.

Remak Since 1/Δ(s)is bounded on the whole real axis,thenΩ(s)∈ ˜H andΩ(s)∈L2(−∞,+∞),henceΩ(s)∈{{0}}and(2.1)has the unique solutionω(t)in class{0}.

§3.On Method of Solution for Singular Integral Equation of Dual Type with Refl ectionω(t)andω(−t)

Let us consider the following equation

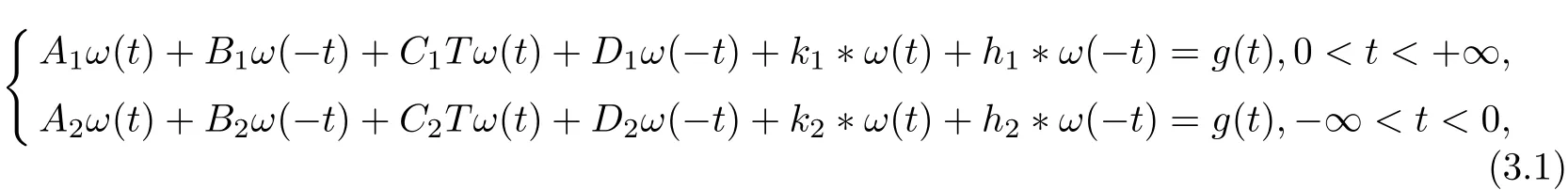
where Aj,Bj,Cj,Djare constants and allthe functions appeared in(3.1)belong to{0}.

In the first equation of(3.1),by extending t to−∞＜t＜+∞,we get an equation

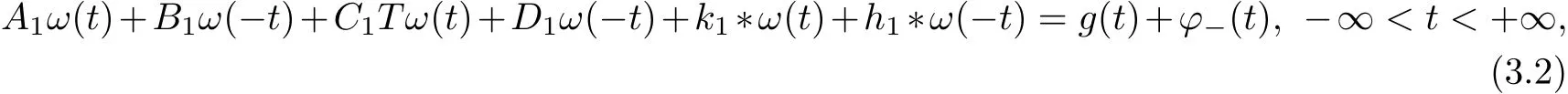
whereϕ−(t)is an unknown function in class{0}withϕ−(t)=0 when 0＜t＜+∞.

Similarly,in the second one of(3.1),by extending t to−∞＜t＜+∞,we have

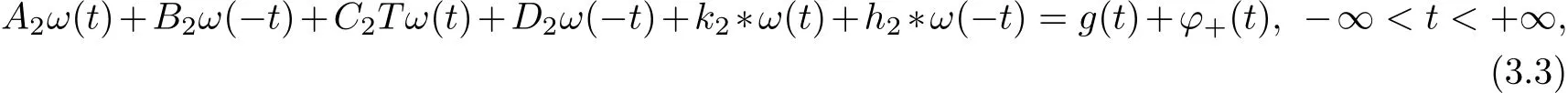
whereϕ+(t)is an unknown function in{0}withϕ+(t)=0 when−∞＜t＜0.

Taking Fourier transform in both(3.2)and(3.3)and denotingΦ+(s)=wϕ+(t),Φ−(s)= wϕ−(t),we get

where

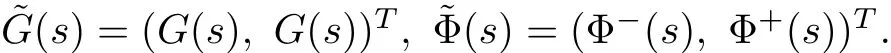
In order thatΩ(s)is continuous at s=0,it is necessary thatΦ±(s)are continuous at s=0 andΦ+(0)=Φ−(0)=−G(0).Note thatΦ±(s)are the boundary values of the Cauchy type integral

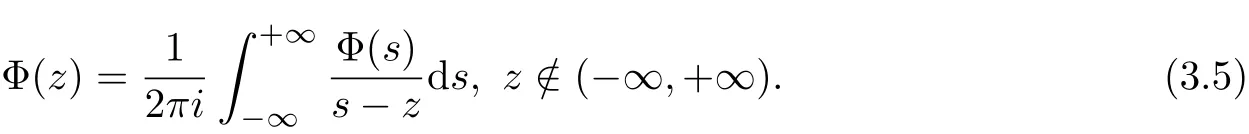
And it is well-known thatΦ±(s)are the one-sided Fourier transforms ofϕ(t)

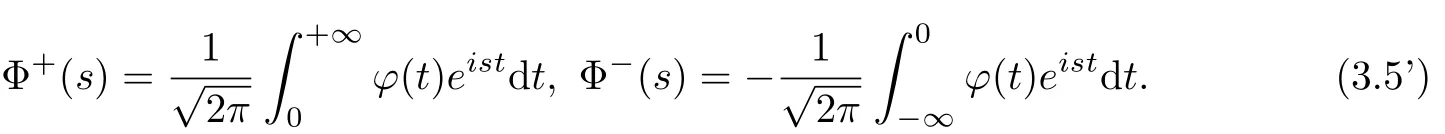
It is evident thatΦ(s)=Φ+(s)−Φ−(s).By eliminating F(±s)in(3.4),we obtain the following Riemann boundary value problem with reflection

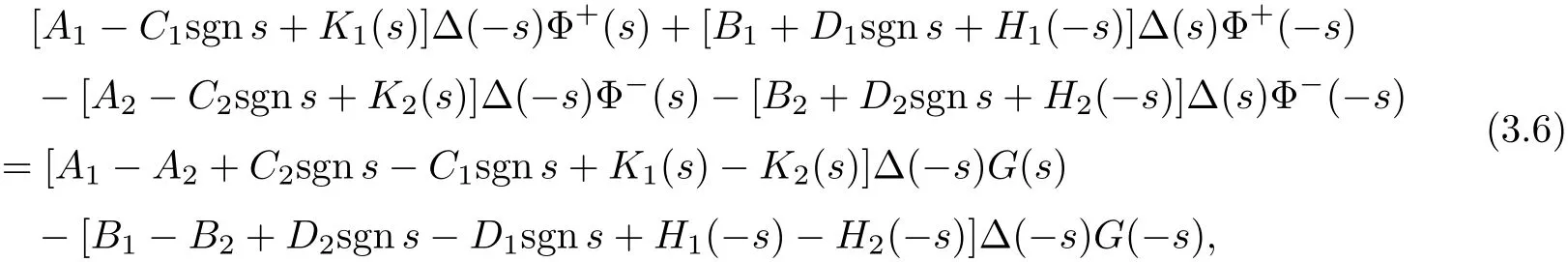
whereΔ(s)=det M(s).Note thatΦ(±∞)=0 are required sinceΦ(s)∈{{0}}.Therefore by using Plemelj formula in(3.5)[6],we have

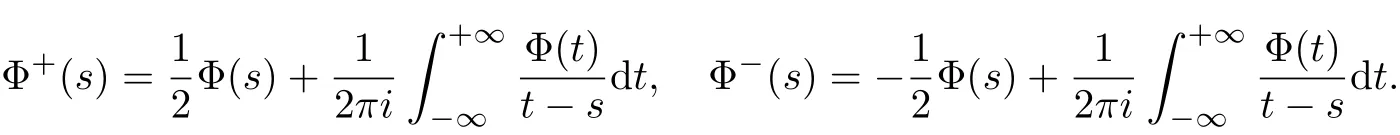
Let

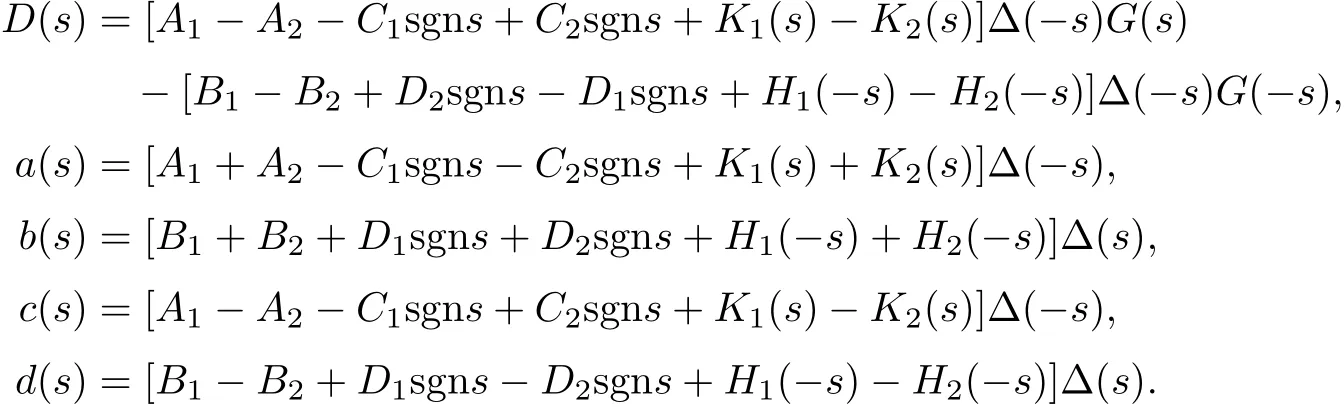
Then,(3.6)may be also reduced to a singular integral equation with reflection

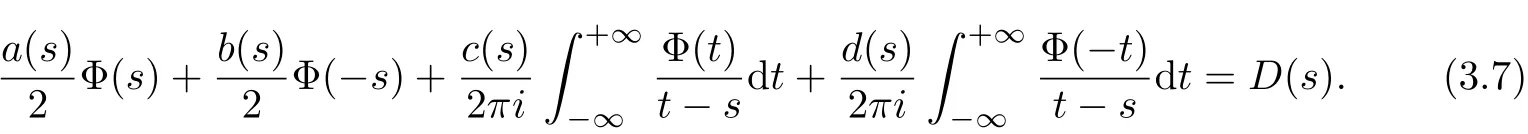
To solve(3.7),we replace s by−s in it and let W(s)=(Φ(s),Φ(−s))T,then a two dimensional singular integralequation in class{{0}}is obtained

where

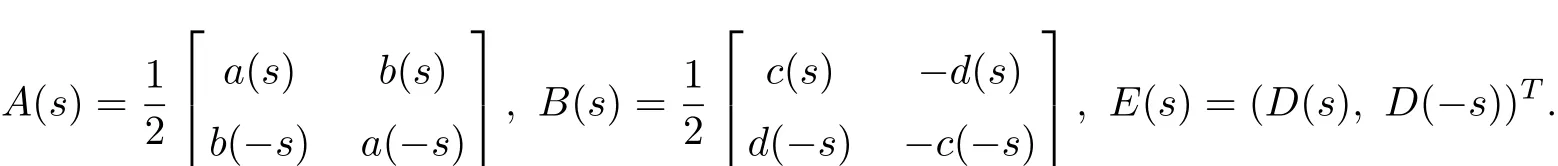
Next we willsolve the equation(3.8).Let

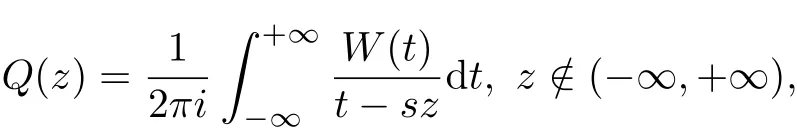
then

Putting(3.9)into(3.8),we may obtain

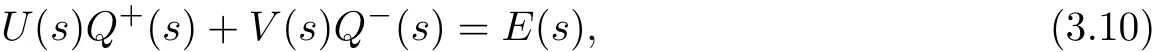
where U(s)=A(s)+B(s),V(s)=A(s)−B(s),Q(s)is a two-dimensional unknown vector function.

We know that(3.7)is solvable if and only if(3.10)is solvable and its solution may be obtained after the latter is solved.In this paper,we consider only the case of normal type, i.e.,det U(s)V(s)/=0 hold on the real axis,therefore we have known that U(s)and V(s)are reversible matrixes.Let

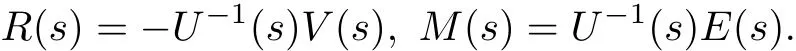
Then(3.10)is transformed to the non-homogeneous Riemann boundary value problem offunctional system

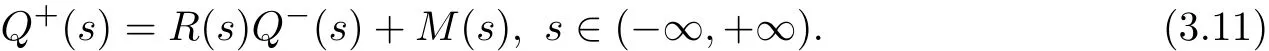
Owing to det R(s)/=0,therefore,(3.11)is the Riemann boundary value problem of the normal case,which satisfies the following conditions

Making linear transformation[7]

Obviously,the inverse transform of(3.13)have the same form.Transform(3.13)maps X onto the circleΓ:|ζ+i/2|=1/2 which surrounds an interior region D+and an exterior region D−, and put the upper half-plane Z+and lower half-plane Z−maps onto D+and D−respectively. (3.11)is readily reduced to the Riemann boundary value problem of a group of function inζ plane by transformation(3.13),

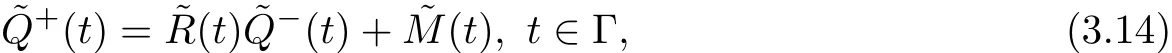
where˜R(t)=R(−it/(t+i)),˜M(t)=M(−it/(t+i))and˜M(−i)=0 with˜R(t)and˜M(t)belong to H onΓ.Hence the boundary value problem(3.14)must fulfillthe additional condition

On the boundary value problem 3.11 and 3.14,we have the following theorem

Theorem 2 If˜Q(ζ)is a bounded solution of boundary value problem(3.14)that satisfies the complementary condition(3.15),then Q(z)=˜Q(−iz/(z+i))must be a bounded solution ofboundary value problem(3.11)that satisfies the complementary condition(3.12),the inverse holds also.

Next we would solve the boundary value problem(3.14)with complementary condition (3.15).

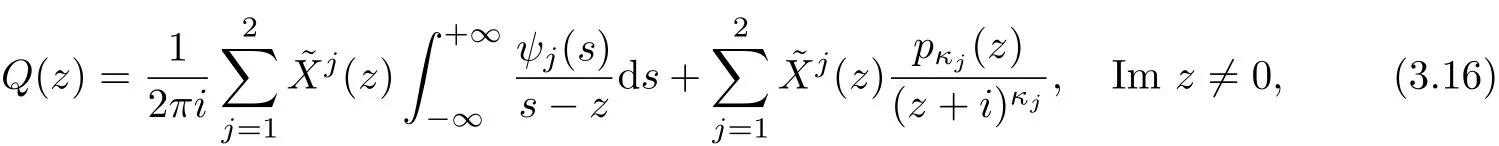
whereψ(s)=[X+(s)]−1M(s)andψj(s)(j=1,2)are two components ofψ(s);X(z)= ˜X(−iz/(z+i))and Xj(z)(j=1,2)are two solution components of X(z);pκj−1(z)is a polynomial of degreeκj−1.

As was stated above,with respect to the boundary value problem(3.14),we have the following result.

Theorem 3 Under the condition(3.15),the solution of problem(3.14)can be expressed by(3.16).In(3.16),if 0≤ κ2≤ κ1,then Q(z)containsκ1+κ2arbitrary constants.If κ2＜κ1≤0,then pκj−1(z)≡0(j=1,2),in this case,the conditions of solvability become,then there are exactlyconditions of solvability.Ifκ2＜0＜κ1,then Q(z)containsκ1arbitrary constants and theconditions of solvability are therefore there are−κ2conditions of solvability with pκ2−1(z)≡0.

Hence,the above processes of solution are summarized as follows

From(3.16),we may obtain Q+(s)and Q−(s)by using Plemelj formula,then substitute Q±(s)into(3.9)and obtain W(s).In fact,assume W(s)=(W1(s),W2(s))Tis a solution of (3.8).Then,it is easily verified that˜W(s)=(W2(−s),W1(−s))Tis also a solution of it and so doesHence

is a solution of(3.7).PutΦ(s)into(3.4),then similar to the discussion in Section 2,we can get the solutionΩ(s),finallyω(t)=ω−1{Ω(s)}is a solution of(3.1).Obviouslyω(t)belongs to class{0}.

§4.Equations with Refl ection and a Finite Set of Translation Shift

The method of solution used above is also in effect for equations similar to(2.1)and(3.1)with both reflection and a finite set of translation shiftω(t+λj)andω(−t−µj),namely,

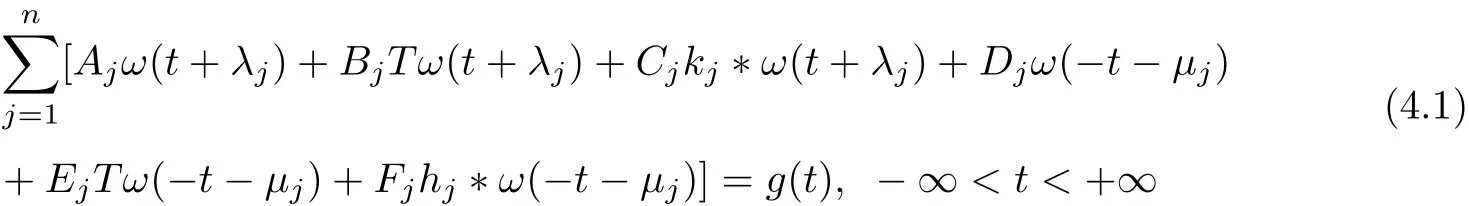
and

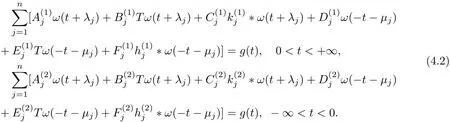
In(4.1)and(4.2),λj,µj(1≤j≤n)and all the coeffi cients appeared in it are constants.By using the Fourier transformation,they all may be transformed into Riemann boundary value problem with discontinuous coeffi cients.The solving method is similar to equation(2.1)or (3.1)mentioned above and further discussions willbe omitted here.

[1]GAKHOV F D,CHERSKY U I.Integral operators of convolution type with discontinuous coeffi cients[J]. Math Nachr,1977,(79):75-78.

[2]LITVINCHUK G S.Singular Integral Equations and Boundary Value Problems with Shift[M].Moscow: Nauka Press,1978:202-207.

[3]LU Jian-ke.On method of solution for some classes of singular integral equations with convolution[J].Chin Ann of Math,1987,8B(1):97-108.

[4]LU Jian-ke.Boundary Value Problems for Analytic Functions[M].Singapore:World Sci,2004.

[5]LU Jian-ke.Some classes boundary value problems and singular integralequations with a transformation[J]. Advances in Mathematics,1994,23(5):424-431.

[6]ZHONG Shou-guo.Several types of formulas to interchanging order of integration for singular integrals of higher order on the real axis[J].J of Math,2000,20(3):355-358.

[7]LI Ping-run.The integral equations containing both cosecant and convolution kernel with periodicity[J].J Sys Sci and Math Scis,2010,30(8):1148-1155.

[8]LI Ping-run.On method ofsolution of non-normaltype for one kind ofsingular integraldiff erentialequations with both convolution kernel and Cauchy kernel[J].J Sys Sci and Math Scis,2013,33(12):1466-1476.

[9]LI Ping-run.On method of solution for two classes of equations of convolution type with harmonic singular operator[J].J Sys Sci and Math Scis,2013,33(7):854-861.

[10]LI Shu-hai,YANG Jian-yu.A class of analytic functions of complex order[J].Chin Quart J of Math,2010, 25(3):414-421.

tion:45E05,45E10

1002–0462(2014)01–0107–09

Chin.Quart.J.of Math. 2014,29(1):107—115

date:2011-09-19

Supported by the Qufu Normal University Youth Fund(XJ201218)

Biography:LI Ping-run(1966-),male,native of Yanzhou,Shandong,a lecturer of Qufu Normal University, Ph.D.,engages in the boundary value problem of analytic function and singular integral equation.

CLC number:O175.5,O175.8 Document code:A