Convexity for New Integral Operator on k-uniformly p-valentα-convex Functions of Complex Order

LI Shu-hai,MA Li-na,AO-en

(School of Mathematics and Statistics,Chifeng University,Chifeng 024001,China)

Convexity for New Integral Operator on k-uniformly p-valentα-convex Functions of Complex Order

LI Shu-hai,MA Li-na,AO-en

(School of Mathematics and Statistics,Chifeng University,Chifeng 024001,China)

In this paper,we obtain the convexity of new general integral operator on some classes of k-uniformly p-valentα-convex functions of complex order.These results extend some known theorems.

analytic functions;p-valently;k-uniformly;starlike;convex;integral operator

§1. Introduction

Let Apdenote the class of functions of the form

which are analytic in the open unit disk U={z∈C:|z|＜1}.The class A1will be denoted by A.

Furthermore,a function f∈Cp(b,β)is p-valently convex of complex order b(b∈C−{0}) and typeβ(0≤β＜p),if it satisfies the following inequality

For p=1,these classes were considered by[1-4].

A function f∈Jp(b,α;β)is p-valentlyα-convex of complex order b(b∈C−{0})and type β(0≤β＜p),if it satisfies the following inequality

Similarly,forβ＞p,the class Mp(b,α;β)reduce respectively to the equivalent class

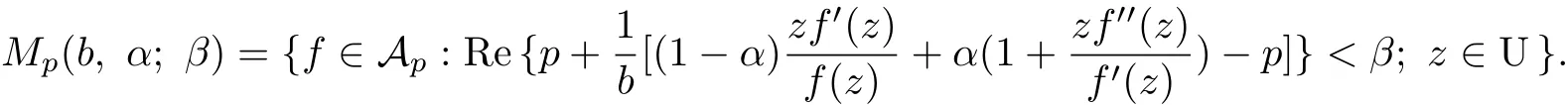
Clearly,we have

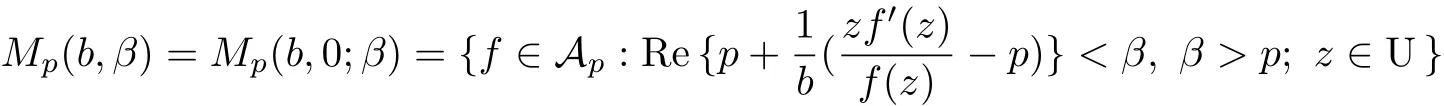
and

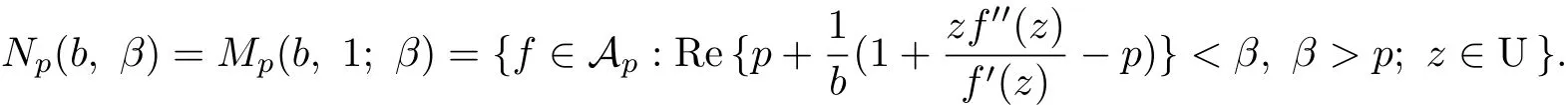
The classes J1(1,α;β)and M1(1,α;β)were studied by Fukui[5].

For functions f and g,analytic in U,we say that f is subordinate to g in U and write

if there exists a Schwarz functionω,which(by definition)is analytic in U withω(0)=0 and |ω(z)|＜1(z∈U),such that f(z)=g(ω(z))(z∈U).Indeed it is known that

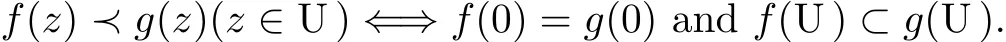
Furthermore,if the function g is univalent in U,then we have the following equivalence[6, P4]:

As usual,we denote by S the subclass of A consisting offunctions which are also univalent in U.Furthermore,we denote by k−U C V and k−S T two interesting subclasses of S consisting, respectively,of functions which are k-uniformly convex and k-uniformly starlike in U.Thus, we have

and

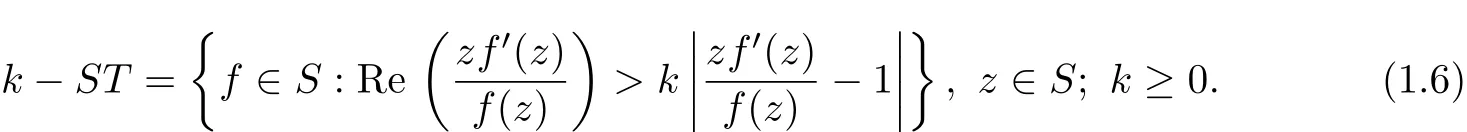
The class k−U C V was introduced by Kanas and Wisniowska[7],where its geometric definition and connections with the conic domains were considered.The class k−S T was investigated in[8].In fact,it is related to the class k−U C V by means ofthe well-known Alexander equivalence between the usualclasses ofconvex and starlike functions(see also the work of Kanas and Srivastava[9]for further developments involving each of the classes k−U C V and k−S T).In particular,when k=1,we obtain

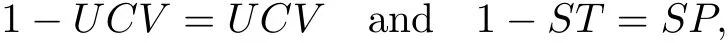
where U C V and S P are the familiar classes ofuniformly convex functions and parabolic starlike functions in U,respectively(see,for details,[10-13]).In fact,by making use of a certain fractionalcalculus operator,Srivastava and Mishra[14]presented a systematic and unified study of the classes U C V and S P.

For a function f∈Ap,we define the following operator

where j∈N0=N∪{0}.The differential operator Djwas introduced by Shenan et al[15].

When p=1,we get Sˇalˇagean diff erential operator(see[16]).

By using the operator Dj,we introduce the new class of p-valent analytic functions.

Defi nition 1.1 Letϕ(z)be an analytic univalent function in U withϕ(0)=1.The class U Jp,j(b,α,k;ϕ)consists of functions f(z)∈Apsatisfying

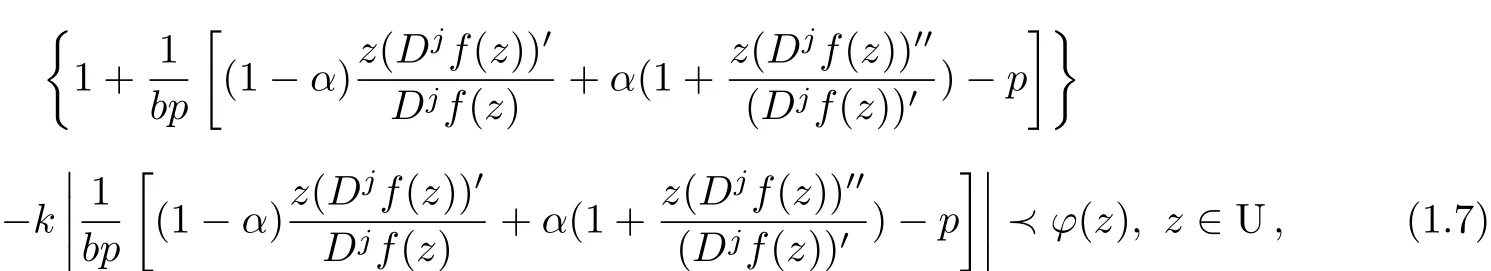
whereα≥0,k≥0,b∈C−{0}.

Letϕ(z)=ϕp,β(z):U→C be the function defined by

Whenβ＜p,ϕp,β(z)is the half-plane defined by Reϕp,β(z)＞,while in the caseβ＞ p,ϕp,β(z)is the half-plane defined by Reϕp,β(z)＜

Thus forβ＜p,the class U Jp,j(b,α,k;ϕp,β)reduce to the familiar class of k-uniformly p-valentα-convex functions of complex order b(b∈C−{0})and typeβ

Similarly,forβ＞p,the class U Jp,j(b,α,k;ϕp,β)reduce to the equivalent class

Setting

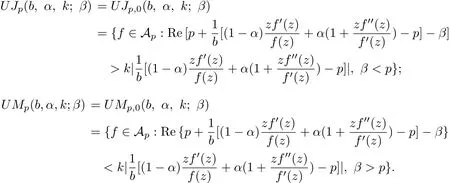
Clearly,we have

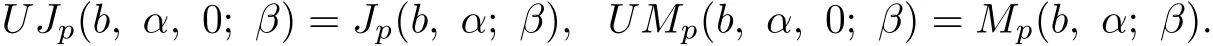
For suitable choices of the functionϕand parametersα,j,k and p involved in the class U Jp,j(b,α,k;ϕ),we also obtain the following subclasses which were studied in many earlier works

(1)U Jp,j(b,0,0;β)(0≤β＜p)and U Jp,j(b,1,0;β)(0≤β＜p)(see[17]).

(2)U Jp,0(1,0,k;β)(0＜k＜1,−k p≤β＜p)(see[18-19]).

(3)U M1(b,0,k;β)(β＞1)and U M1(b,1,k;β)(β＞1)(see[20]).

(4)U J1,0(1,0,k;ϕ)and U J1,0(1,1,k;ϕ)(see[21]).

(5)U Jp,0(1,0,0;β)(0≤β＜p)and U Jp,0(1,1,0;β)(0≤β＜p)(see[22-23]).

(6)U J1(1,1,k;β)and U J1,0(1,0,k;β)(k≥0,−1≤β＜1)(see[24]).

The second family of integral operators was introduced by D Breaz and N Breaz[25]and it has the following form(see also a recent investigation on this subject by D Breaz et al[26]

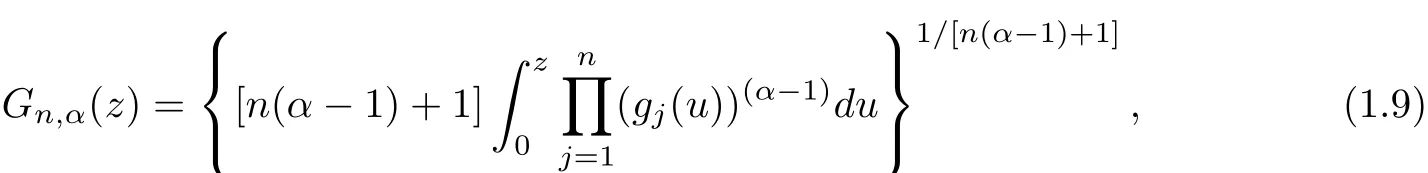
whereα∈C,Reα＞0;gj∈A;j=1,2,···,n.

Forλi＞0,α≥0 and fi(z)∈Ap,we define the following general integral operators

Remark 1.1 Takingα=0 andα=1,we obtain the generalintegraloperators Fn,p(j,0;z) and Fn,p(j,1;z)introduced and studied by G¨ulsah Saltik et al[17].Forα=0,j=0 andα= 1,j=0,we obtain the general integral operators Fn,p(0,0;z)and Fn,p(0,1;z)introduced and studied by B A Frasin[18].And for p=1,we obtain the general integral operators Fn,1(0,0;z) and Fn,1(0,1;z)introduced and studied by Breaz et al[1,2730].

In[31],Li and Yang investigated a class of analytic functions of complex order.

In this paper,we obtain the order of convexity of the operator Fn,p(j,α;z)on the class U Jp,j(b,α,k;β),continue and extend the considerations of the paper[17-18].

§2.Main Results

First,we prove the following inclusion relation.

Theorem 2.1 For k≥0,β＜p,b∈C−{0},let f(z)∈U Jp,j(b,α,k;β),then

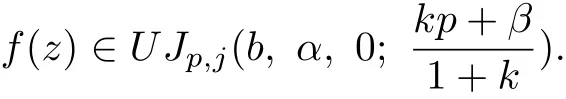
Proof Let f(z)∈U Jp,j(b,α,k;β).Then the quantity

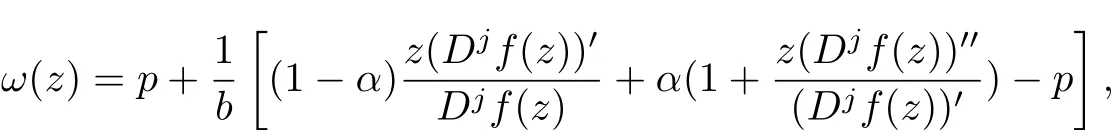
satisfies

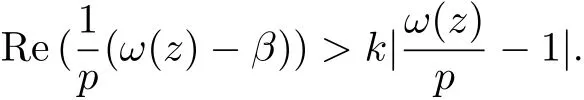
The inequality

yields

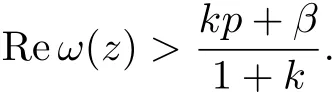
Thus

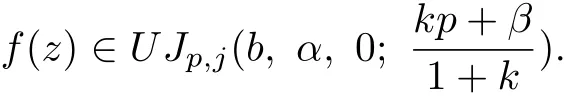
Theorem 2.2 Letλi＞0,αi≥0,ki≥0,−1≤βi＜p for all i=1,2,···,n and fi(z)∈U Jp,j(b,αi,ki;βi)for all i=1,2,···,n.If

then the integral operator Fn,p(j,αi;z)is p-valently convex of order b and type

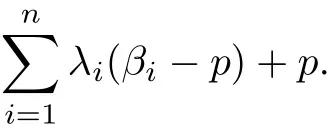
Proof From the definition(1.10),we observe that Fn,p(j,αi;z)∈Ap.On the other hand, it is easy to see that

Now we diff erentiate(2.2)logarithmically and multiply by z,we obtain

Then multiplying the relation(2.3)with

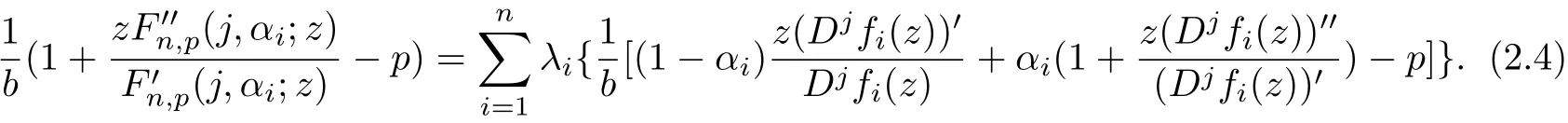
The relation(2.4)is equivalent to

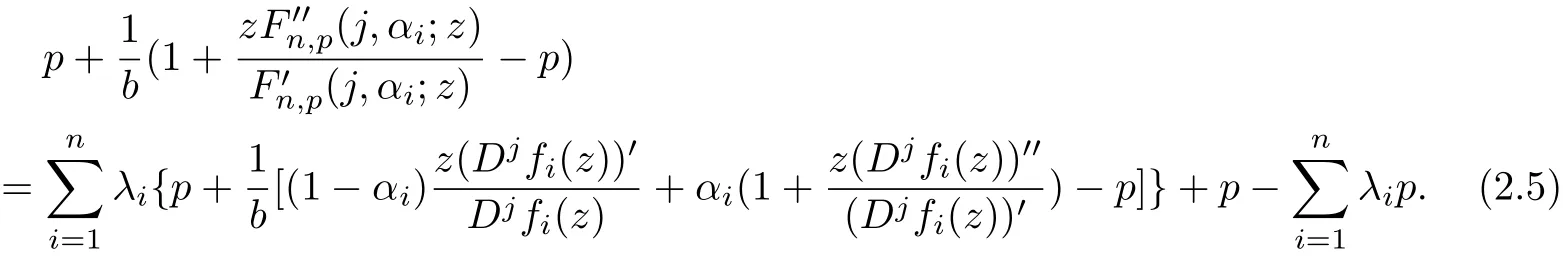
Taking the real part of both sides of(2.5),we have

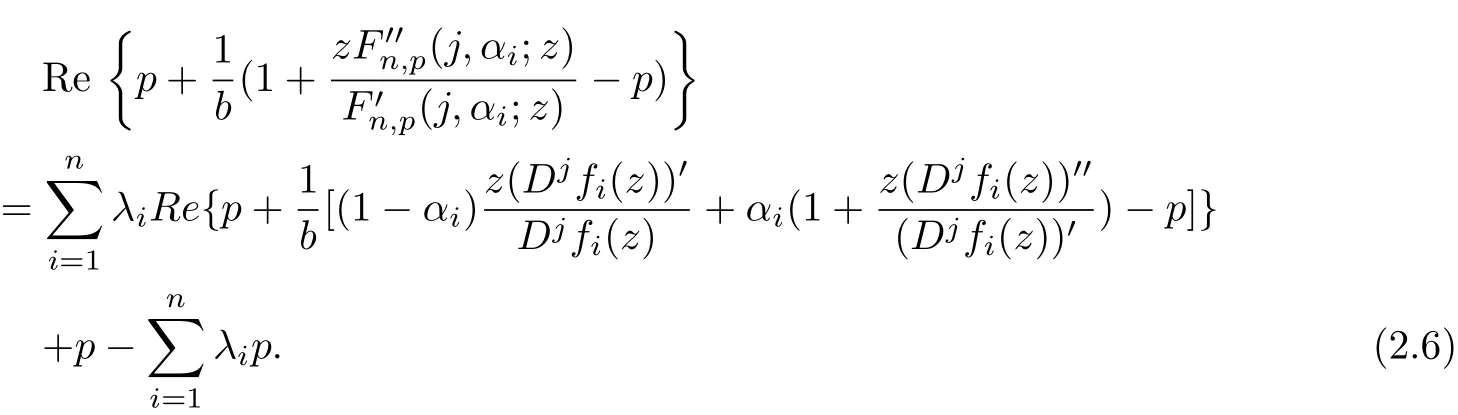
Since fi(z)∈U Jp,j(b,αi,ki;βi)for all i=1,2,···,n,from(2.6),we have

Because

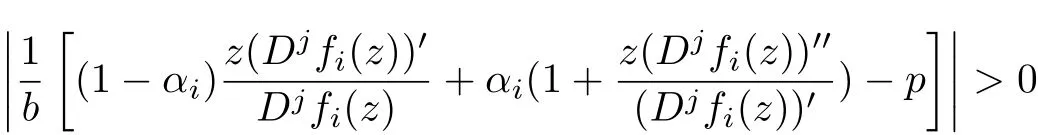
for all i=1,2,···,n,we obtain

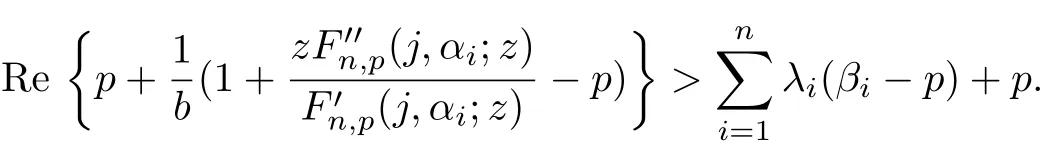
Therefore Fn,p(j,αi;z)is p-valently convex of complex order of b and type

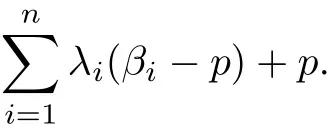
This evidently completes the proof of Theorem 2.2.

Remark 2.1 Lettingαi=0,ki=0 and 0≤βi＜p for all i={1,2,···,n}in Theorem 2.2,we improve Theorem 2.1 in[17].

Lettingαi=1,ki=0 and 0≤βi＜p for all i={1,2,···,n}in Theorem 2.2,we improve Theorem 3.1 in[17].

Lettingαi=0,j=0,b=1 and−1≤βi＜p for all i={1,2,···,n}in Theorem 2.2,we obtain Theorem 2.1 in[18].

Lettingαi=1,j=0,b=1 and−1≤βi＜p for all i={1,2,···,n}in Theorem 2.2,we obtain Theorem 3.1 in[18].

Corollary 2.1 Letλi＞0,ki≥0,−1≤βi＜p and fi(z)∈U Jp,j(b,0,ki;βi)for all i=1,2,···,n.If

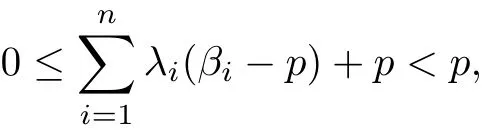
then the integraloperator Fn,p(j,0;z)is p-valently convex of order b and type

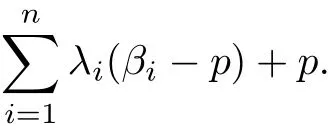
Theorem 2.3 Letλi＞0,αi≥0,ki≥0,−1≤βi＜p,fi(z)∈U Jp,j(b,αi,ki;βi)for all i=1,2,···,n and

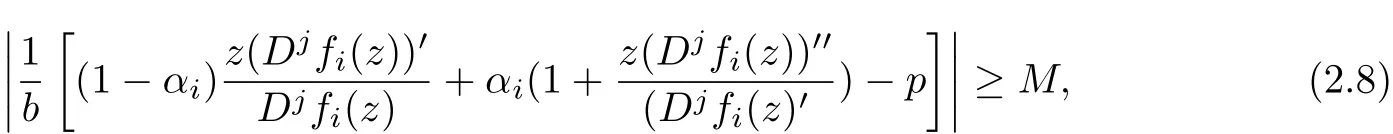
where

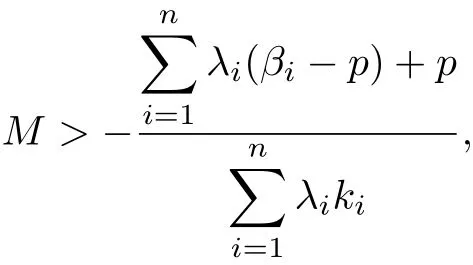
for all i=1,2,···,n.Then the integral operator Fn,p(j,αi;z)is p-valently convex of order b in U.

Proof From(2.7)and(2.8)we easily get Fn,p(j,αi;z)∈Cp(b,0).

Remark 2.2 Lettingαi=0,j=0 and b=1 in Theorem 2.3,we obtain Theorem 2.4 in [18].

Theorem 2.4 Letλi＞0,αi≥0,ki≥0,βi＞p and fi(z)∈U Mp,j(b,αi,ki;βi)for all i=1,2,···,n.If

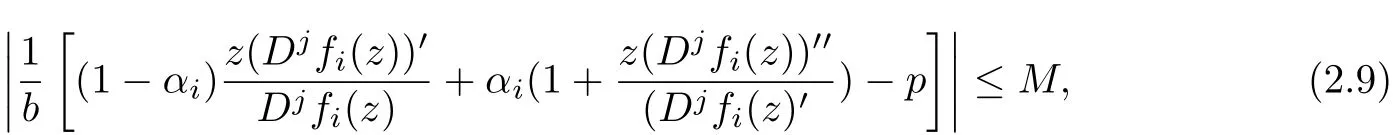
where

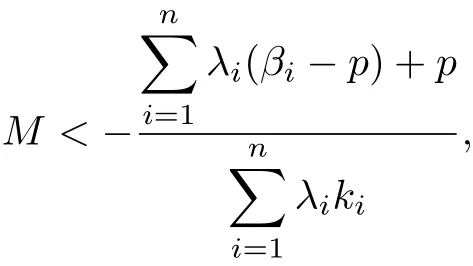
for all i=1,2,···,n,then the integral operator Fn,p(j,αi;z)∈Mp(b,0).

Proof From(2.7)and(2.9)we easily get Fn,p(j,αi;z)∈Mp(b,0).

We remark in conclusion that,by suitably specializing the parameters involved in the results presented in this paper,we can deduce numerous further corollaries and consequences of each of these results.

[1]BREAZ D,G¨UNEYH¨O.The integral operator on the classes S∗α(b)and Cα(b)[J].Journal of Mathematical Inequalities,2008,2(1):97-100.

[2]BREAZ D,AOUF M K,BREAZ N.Some properties for integral operators on some analytic functions with complex order[J].Acta Mathematica Academiae Paedagogicae Ny´ıregyh´aziensis,2009,25:39-43.

[3]BULUT S.A note on the paper of Breaz and G¨uney[J].Journal of Mathematical Inequalities,2008,2(4): 549-553.

[4]FRASIN B A.Family of analytic functions of complex order[J].Acta Mathematica Academia Paedagogicae Ny´ıregyh´aziensis,2006,22:179-191.

[5]FUKUI S.Onα-convex functions of orderβ[J].International Journal of Mathematics and Mathematical Sciences,1997,20(4):769-772.

[6]MILLER S S,MOCANU P T.Diff erential Subordinations:Theory and Applications[C].New York:Marcel Dekker,2000.

[7]KANAS S,WISNIOWSKA A.Conic regions and k-uniform convexity[J].Journal of Computational and Applied Mathematics,1999,105:327–336.

[8]KANAS S,WISIOWSKA A.Conic regions and k-starlike functions[J].Rev Roumaine Math Pures Appl, 2000,45(4):647-657.

[9]KANAS S,SRIVASTAVA H M.Linear operators associated with k-uniformly convex functions[J].Integral Transforms and Special Functions,2000,9:121-132.

[10]GOODMAN A W.On uniformly convex functions[J].Ann Polon Math,1991,56:87-92.

[11]GOODMAN A W.On uniformly starlike functions[J].J Math Anal Appl,1991,155:364-370.

[12]MA Wan-cang,MINDA D.Uniformly convex functions[J].Ann Polon Math,1992,57:165-175.

[13]RONNING F.Uniformly convex functions and a corresponding class of starlike functions[J].Proc Amer Math Soc,1993,118(1):189-196.

[14]SRIVASTAVA H M,MISHR A K.Applications of fractional calculus to parabolic starlike and uniformly convex functions[J].Computers and Mathematics with Applications,2000,39:57-69.

[15]SHENAN G M,SALIM T O,MAROUF M S.A certain class of multivalent prestarlike functions involving the Srivastava-Saigo-Owa fractional integral operator[J].Kyungpook Math J,2004,44:353-362.

[16]SAlAGEAN G S.Subclasses of Univalent Functions[C].New York:Springer-Verlag,1983:362-372.

[17]SALTIK G,DENIZ E,KADIOˇGLU E.Two new general p-valent integral operators[J].Mathematical and Computer Modelling,2010,52:1605-1609.

[18]FRASIN B A.Convexity of integral operators of p-valent functions[J].Mathematical and Computer Modelling,2010,51:601-605.

[19]YANG Ding-gong,OWA S.Properties of certain p-valent convex functions[J].International Journal of Mathematics and Mathematical Sciences,2003,41:2603-2608.

[20]NISHIWAKI J,OWA S.Certain classes of analytic functions concerned with uniformly starlike and convex functions[J].Applied Mathematics and Computation,2007,187(1):350–355.

[21]MA Wan-cang,MINDA D.A Unified Treatment of Some Special Classes of Univalent Functions[C].Cambridge:Internat Press,1994:157-169.

[22]ALI R M,LEE S K,RAVICHANDRAN V.Subclasses of multivalent starlike and convex functions[J]. Bulletin of Belgian Mathematical Society-Simon Stevin,2009,16(3):385-394.

[23]AL-KHARSANI H A,AL-HAJIRY S S.A note on certain inequalities for p-valent functions[J].J of Inequal in Pure and Appl Math,2008,9(3):Art.90.

[24]AGHALARY R,JAHANGIRI J M.Inclusion relations for k-uniformly starlike and related functions under certain integral operators[J].Bull Korean Math Soc,2005,42(3):623-629.

[25]BREAZ D,BREAZ N.Univalence of an integral operator[J].Mathematica(Cluj),2005,47(70):35-38

[26]BREAZ D,BREAZ N,SRIVASTAVA H M.An extension of the univalent condition for a family of integral operators[J].Applied Mathematics Letters,2009,22(1):41-44.

[27]BREAZ D,BREAZ N.Two integral operator[J].Stud Univ Babes-Bolyai Math,2002,47(2):13-21.

[28]BREAZ D,OWA S,BREAZ N.A new integral univalent operator[J].Acta Univ Apulensis Math,2008,16: 11–16.

[29]BREAZ D.A convexity properties for an integral operator on the class Sp(β)[J].Gen Math,2007,15: 177–183.

[30]FRASIN B A.Some suffi cient conditions for certain integral operators[J].Journal of Mathematical Inequalities,2008,2(4):527–535.

[31]LI Shu-hai,YANG Jing-yu.A class of analytic functions of complex order[J].Chin Quart J of Math,2010, 25(3):414–421.

tion:30C45,30C50,26D15

1002-0462(2014)01–0088–09

Chin.Quart.J.of Math. 2014,29(1):88—96

date:2013-01-21

Supported by the Natural Science Foundation of Inner Mongolia(2009MS0113);Supported by the Higher School Research Foundation of Inner Mongolia(NJzy08150)

Biographies:LI Shu-hai(1966-),male(mongolian),native of Chifeng,Inner Mongolia,a professor of Chifeng University,engages in geometric function theory and applications;MA Li-na(1982-),female(mongolian),native of Chifeng,Inner Mongolia,a lecturer of Chifeng University,M.S.D.,engagesin harmonic analysis;AO-en(1980-), female(mongolian),native of Chifeng,Inner Mongolia,a lecturer of Chifeng University,M.S.D.,engages in complex analysis.

CLC number:O174.51 Document code:A