An Extrapolated Parallel Subgradient Projection Algorithm with Centering Technique for the Convex Feasibility Problem

DANG Ya-zheng,HAN Xue-feng,GAO Yan

(1.School of Management,University of Shanghai for Science and Technology,Shanghai200093,China; 2.College of Compiler Science and Technology,Henan Polytechnic University,Jiaozho 454000,China)

An Extrapolated Parallel Subgradient Projection Algorithm with Centering Technique for the Convex Feasibility Problem

DANG Ya-zheng1,2,HAN Xue-feng2,GAO Yan1

(1.School of Management,University of Shanghai for Science and Technology,Shanghai200093,China; 2.College of Compiler Science and Technology,Henan Polytechnic University,Jiaozho 454000,China)

In this paper,we present an extrapolated parallelsubgradient projection method with the centering technique for the convex feasibility problem,the algorithm improves the convergence by reason of using centering techniques which reduce the oscillation of the corresponding sequence.To prove the convergence in a simply way,we transmit the parallel algorithm in the original space to a sequential one in a newly constructed product space. Thus,the convergence of the parallel algorithm is derived with the help of the sequentialone under some suitable conditions.Numerical results show that the new algorithm has better convergence than the existing algorithms.

convex feasibility problem;subgradient;centering technique;product space; convergence

§1. Introduction

Convex feasibility problem(CFP)is to find a point

where C={fi(x)≤0,i=1,···,m},fi:ℜn→ℜ(i=1,···,m)are convex.

The CFP has many applications in some diverse areas of mathematics and engineering technology,for instance optimization[12],approximation theory[3],image reconstruction from projections and computerized tomography[45],control problem[6]and so on.It is not possible to obtain a point inin a direct manner,a usual iterative procedure is orthogonalprojection.Over the years,there came out many projection algorithms for solving the CFP,see[710].However,in some cases,it is impossible to exactly compute the orthogonalprojection.One usefulpath to circumvent this case is using subgradient projections which depends on computing of subgradients at the current iterative point,e.g.,the cyclic subgradient projections(CSP)[1],parallel subgradient projections(PSP)[11],Eremin’s algorithmic scheme[12]and block-iterative subgradient projection algorithm[13].It has been shown in[11]the convergence of the parallel subgradient projection algorithm with extrapolated factor is much faster than that of general algorithm,while when the iterative element is much closer to the constrains than to the point to be projected,the eff ectiveness of the extrapolation will be weakened in that the sequence generated by the extrapolated parallel subgradient projection algorithm oscillates around the solution set.In this paper,we present an extrapolated parallel subgradient projection method with centering technique which can reduce the oscillations and improve convergence.Moreover,to prove the convergence in a simply way,we transmit the parallel algorithm in the original space to a sequential one in a newly constructed product space based on the idea of Pierra in[14].Thus,the convergence of the parallel algorithm is derived with the help of the sequential one under some suitable conditions.

§2. Preliminaries

Recall the following concepts and lemmas.

Defi nition 2.1 For the given nonempty closed convex subset C inℜn,the orthogonal projection fromℜnonto C is defined as

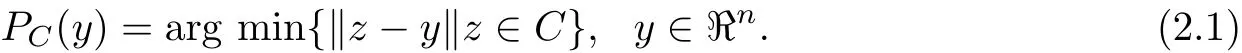
It has the following well-known properties.

Lemma 2.1 Let C be a nonempty closed convex subset inℜn,then for any x∈ℜnand z∈C

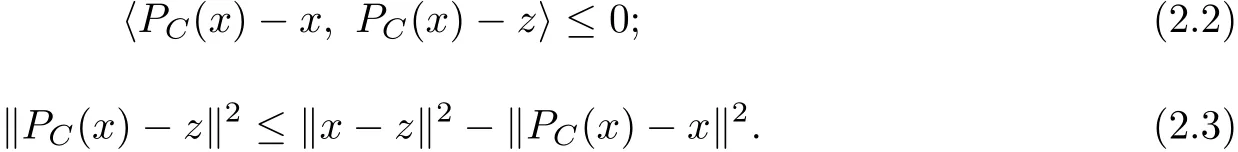
Defi nition 2.2 Let f:ℜN→ℜbe convex.The subdiff erential of f at x is defined as

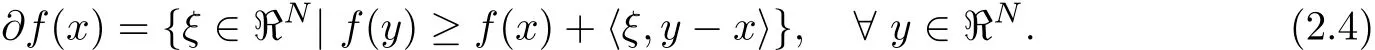
Evidently,an element of∂f(x)is said to be an subgradient.

Lemma 2.2[7]Suppose Ci={x∈ℜN|fi(x)≤0}is nonempty,for anydefine the half spaceby

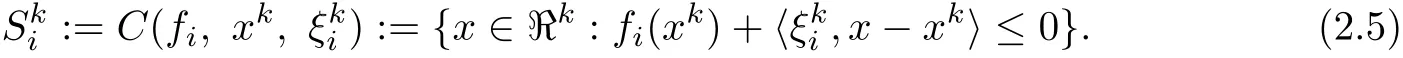
Lemma 2.3[15]Suppose function f:ℜN→ ℜis convex,then its subdifferentials are uniformly bounded set ofℜN.

§3.Algorithms Describe

3.1 Algorithm

Algorithm 3.1

Initialization x0∈ℜnis arbitrary.Let N,J be positive integer numbers,N＞2,J＞N.

Iterative Step Given xk,i∈Ik,Ik={j|fj(xk)≥0,j=1,2,···,m},calculate

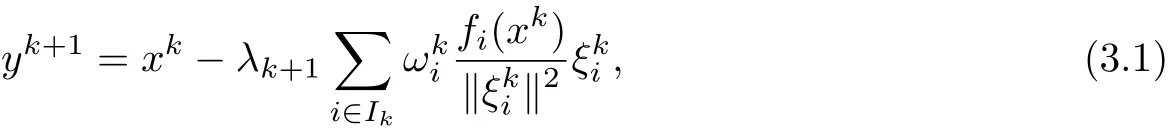
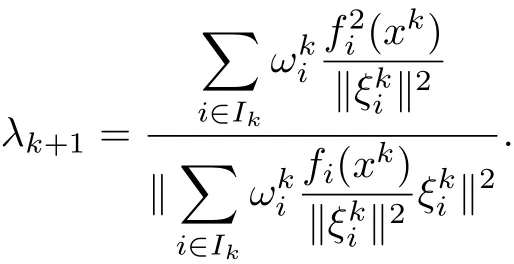
Then

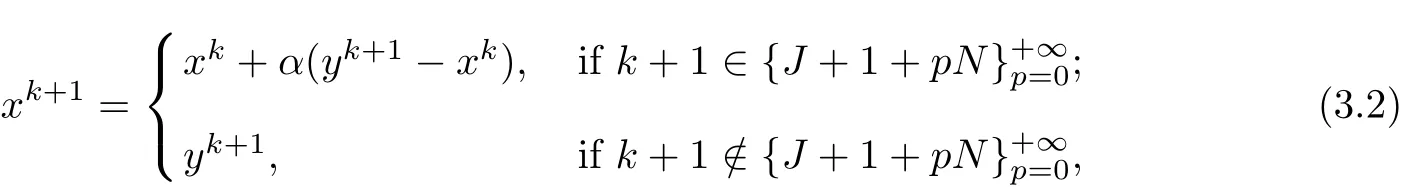
whereα∈(0,1).

3.2 Construction of the New Product-space Let

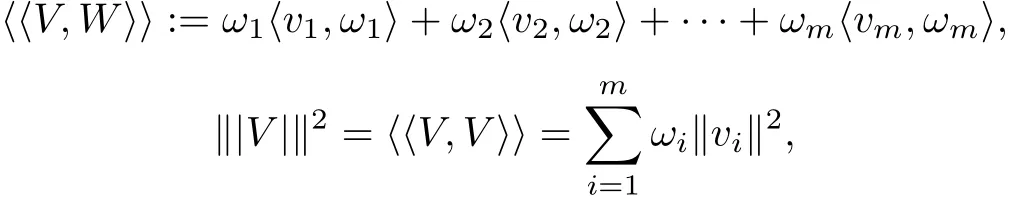
where V=(v1,v2,···,vm)∈(ℜn)m,W=(w1,w2,···,wm∈(ℜn)m.Then,we obtain a product space((ℜn)m,〈〈,〉〉,‖|·|‖)with norm‖|·|‖derived from the inner product〈〈,〉〉.We denote((ℜn)m,〈〈,〉〉,‖|·|‖)for short by H and denote the points in H by capitalletters.

Now we introduce two subsets of the defined space H.One is N≡C1×C2×···×Cm(the Cartesian product of the convex sets(Ci)1≤i≤minℜn)of the space H.It is a closed convex subset of H.Projection onto N is denoted as PN.The other one is D which is the image ofℜnunder the canonicalimbedding q=ℜn→(ℜn)m,where for v∈ℜn,we put q(v)≡(v,v,···,v). D is also a diagonal vector subspace of H.Projection onto D is denoted as PD.

Clearly,if C/=∅,we have that N∩D/=∅,moreover,q(C)=N∩D.Hence,obtaining a point in C⊂H is equivalent to obtaining a point in N∩D⊂H.

3.3 Switching the Parallel Algorithm to a Sequential One

In order to construct sequentialsubgradient projection algorithm in space H,we need some lemmas below

Lemma 3.1[11]Let V≡(v1,v2,···,vm)∈H,then

(2)PNV=(P1v1,P2v2,···,Pmvm).

Lemma 3.1 implies that the operator PDis linear.

Proof By lemmas 2.2 and 3.1,it is easy to get the conclusion of the theorem.

Algorithm 3.2 A given starting point x0inℜnfor the parallel projection method,the point q(x0)belongs to D.We consider this point q(x0)as the starting point for a sequential one in H.Let N,J be positive integer numbers,N＞2,J＞N.Defined the following iteration

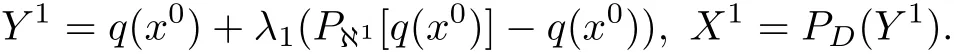
In a general manner,when Xk∈D has already been obtained,put

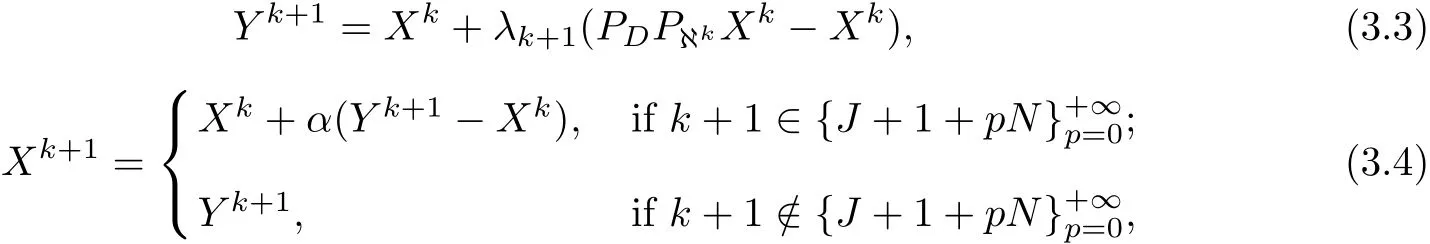
whereα∈(0,1),

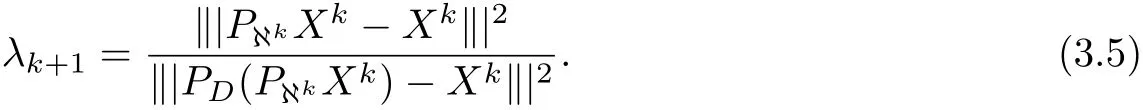
§4.Convergence Analysis

Fact 4.1 Put¯Yk+1=Xk−λk+1PℵkXk,then

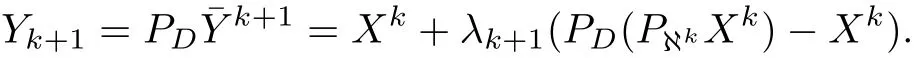
Fact 4.2 Define the hyperplane Lk+1

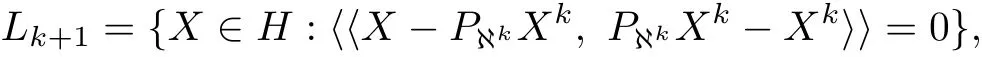
it is orthogonalto Xk−PℵkXkand it goes through the point PkℵXk. Theorem 4.1 For each Z∈ℵ∩D,we have

Proof We will discuss the following two cases

Case I For Xk+1=Yk+1.

By the property of projection(2.2)and Fact 4.2,we have

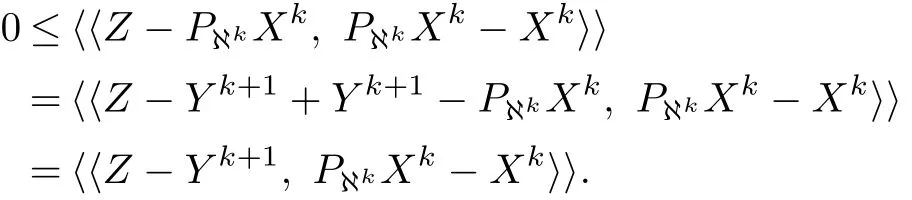
Since PDis linear,from(3.3),we have

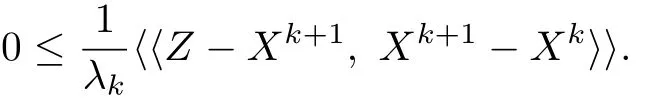
Case II For Xk+1=Xk+α(Yk+1−Xk).By calculating,we have

Lemma 4.1 For Z∈ℵ∩D,

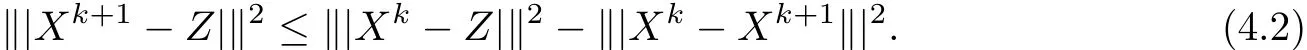
Proof For each point Z∈D∩N,we have

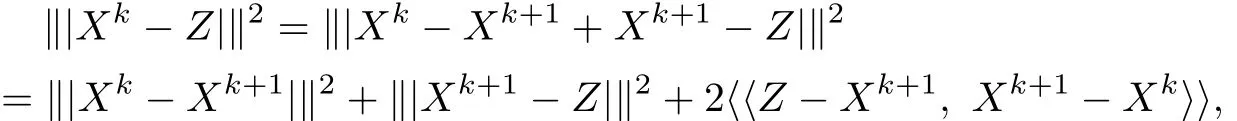
which,due to(4.1),leads to

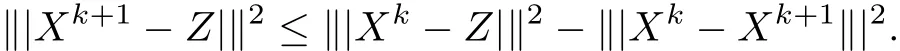
From(4.2)we derive that

Theorem 4.2 Ifℵ∩D/=∅,for the sequencewe have that

Proof We will still consider two cases

Case I For Xk+1=Yk+1.Since Xk+1belongs to the hyperplane which is orthogonalto Xk−PℵkXk,the Pythagorean theorem leads to

By(4.3),we get(4.4).

Case II For Xk+1=Xk+α(Yk+1−Xk),we have

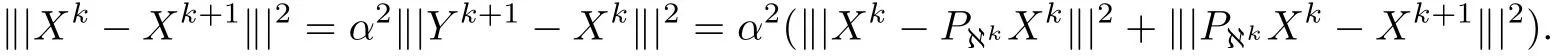
Hence,we also get(4.4)by(4.3).

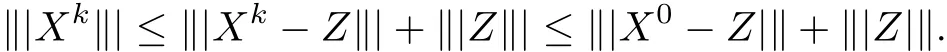
by the algorithm 3.1 converges to a point in the intersection

Proof From above,we know the sequence{Xk}is bounded,then there exists a subsequence{Xkp}of it and a point A in H such that{Xkp}weakly converges to A.

We first show that each convergent subsequence of{Xk}converges to the same point A. Suppose that there exists a subsequence{Xkp′}of{Xk}that is convergent to point A′.For p∈Z+,we obtain

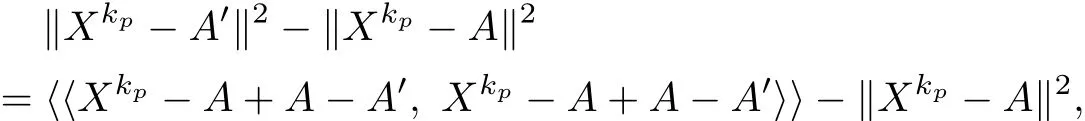
which,after calculating the inner product,leads to

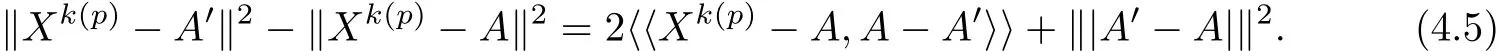
Similarly,for p′∈Z+we get

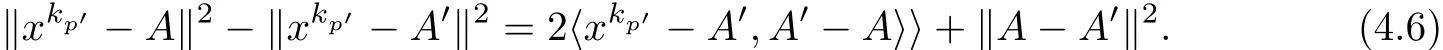
We have known that the sequences{‖Xk−A‖}and{‖|Xk−A′|‖}converge to limits d(A)and d(A′).In particular,

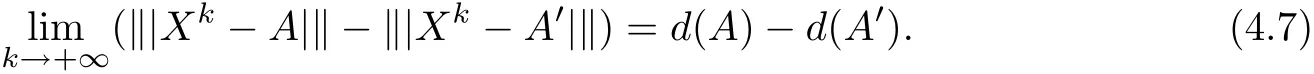
Taking the limits of(4.5)and(4.6),respectively for p→+∞and for p′→+∞,we obtain

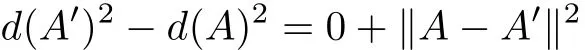
and

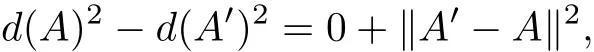
hence,we conclude that A=A′.

From Lemma 2.3,we get

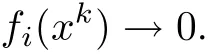
for i=1,2,···,m and k→∞.By continuity of fi(x),we get

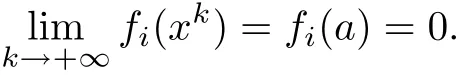
§5.Numerical Experiment

We take the following example to compare the convergence of the algorithm 3.1(denoted by CPSP)with that of the general accelerated parallel subgradient projection algorithm(denoted by PSP).The algorithms stop whenfor all i=1,···,m withε=10−4.We take equal weights|Ik|denotes the number of index of Ik.In CPSP,select N=5,J= 3,α=0.6.

Freudenstein and Roth function with n=2,m=2,

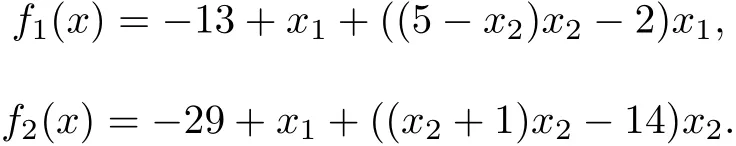
Consider the following three cases

Case 1 x0=(10,4);

Case 2 x0=(100,40);

Case 3 x0=(1000,400).

We list the number of iterations needed by diff erent algorithms in Table 1.

Table 1

From Table 1 as above,the following conclusions can be obtained(1)CPSP converges faster than PSP;(2)It is much easier to implement than the projection algorithm;(3)In the PSP, for some iterations the extrapolation loses its eff ectiveness.Hence,it is worth centering the iteration from time to time in CPSP.

[1]CENSOR Y,LENT A.Cyclic subgradient projections[J].Math Programming,1982,24:233-235.

[2]CHINNECK J W.The constraint consensus method for finding approximately feasible points in nonlinear programs[J].Informs J Comput,2004,16:255-265.

[3]DEUTSCH F.The Method of Alternating Orthogonal Projections,Approximation Theory[M].Dordrecht: Kluwer Academic Publishers,1992:105-121.

[4]CENSOR Y.Parallel application of block iterative methods in medical imaging and radiation therapy[J]. Math Programming,1988,42(1/2):307-325.

[5]HERMAN G T.Image Reconstruction From Projections:The Fundamentals of Computerized Tomography[M].New York:Academic Press,1980.

[6]GAO Yan.Determining the viability for a affi ne nonlinear control system[J].Journal of Control Theory and Applications(in Chinese),2009,29:654-656.

[7]DANG Ya-zhang,GAO Yan.Non-monotonous accelerated parallel subgradient projection algorithm for convex feasibility problem[J].Optimization doi:org/10.1080/02331934.2012.677447.

[8]LI Li,GAO Yan.Projection algorithm with line search for solving the convex feasibility problem[J].Journal of Information and Computing Science,2008,3:62-68.

[9]DANG Ya-zhang,GAO Yan.A strongly convergent algorithm for the convex feasibility problem(in Chinese)[J].Acta Mathematica Applicant Sinica,2011,34(2):303-312.

[10]DANG Ya-zheng,GAO Yan.Inertial projection algorithms for convex feasibility problem[J].Journal of Systems Engineering and Electronics,2012,23(5):734C740.

[11]SANTOS L T.A parallel subgradient projections method for the convex feasibility problem[J].J Comput Appl Math,1987,18:307-320.

[12]EREMIN I I.On systems of inequalities with convex functions in the left sides[J].Amer Math Soc Trans, 1970,88:67-83.

[13]DANG Ya-zheng,GAO Yan.Block-iterative subgradient projection algorithms for the convex feasibility problems[J].OR Transactions,2011,15(1):59-70.

[14]PIERRA G.Decomposition through formalization in a product space[J].Mathematical Programming,1984, 28:96-115.

[15]GAO Yan.Nonsmooth Optimization(in Chinese)[M].Beijing:Science Press,2008.

tion:49M37,90C25,90C90

1002–0462(2014)01–0022–08

Chin.Quart.J.of Math. 2014,29(1):22—29

date:2013-01-01

Supported by the NNSF of China(11171221);Supported by the Shanghai Municipal Committee of Science and Technology(10550500800)

Biographies:DANG Ya-zheng(1973-),female,native Xuchang,Henan,an associate professor of Henan Polytechnic University,engages in optimization;HAN Xue-feng(1981-),male native of Puyang,Henan,a lecturer of Henan Polytechnic University,engages in optimization;GAO Yan(1962-),male,native of Wuchang, Heilongjiang,a professor of University of Shanghai for Science and Technology,engages in optimization and control.

CLC number:O221 Document code:A