A Descent Gradient Method and Its Global Convergence

LIU Jin-kui

(School of Mathematics and Statistics,Chongqing Three Gorges University,Wanzhou 404100,China)

A Descent Gradient Method and Its Global Convergence

LIU Jin-kui

(School of Mathematics and Statistics,Chongqing Three Gorges University,Wanzhou 404100,China)

Y Liu and C Storey(1992)proposed the famous LS conjugate gradient method which has good numerical results.However,the LS method has very weak convergence under the Wolfe-type line search.In this paper,we give a new descent gradient method based on the LS method.It can guarantee the suffi cient descent property at each iteration and the global convergence under the strong Wolfe line search.Finally,we also present extensive preliminary numerical experiments to show the effi ciency of the proposed method by comparing with the famous PRP+method.

unconstrained optimization;conjugate gradient method;strong Wolfe line search;suffi cient descent property;global convergence

§1. Introduction

Consider the unconstrained optimization problem

where f:Rn→ R is continuously differentiable nonlinear function.The conjugate gradient method is one of the effective methods to solve the above problem and its iteration formulas

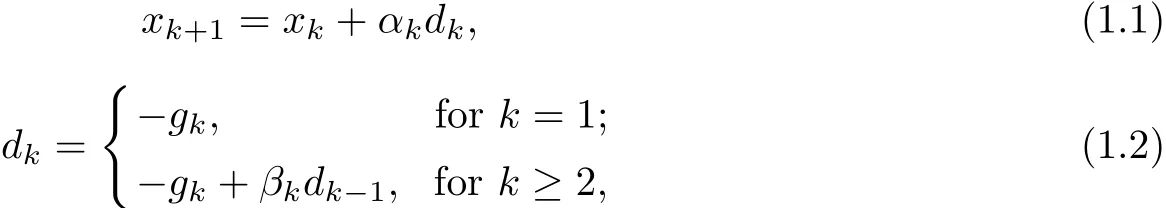
where gk=▽f(xk),αk＞0 is a step length determined by some line search,dkis the search direction andβkis a scalar.Some well-known conjugate gradient methods include Liu-Storey(LS) method[1]and Polak-Ribi`ere-Polyak(PRP)method[23].The parametersβkof these methods are specified as follows

where||·||is the Euclidean norm.Obviously,if f is a strictly convex quadratic function,the above methods are equivalent in the case that an exact line search is used.If f is non-convex, their behaviors may be further different.

In the past few years,the PRP method has been regarded as the most effi cient conjugate gradient method in practical computation.One remarkable property of the PRP method is that it essentially performs a restart if a bad direction occurs(see[4]).However,Powell[5]pointed out that the PRP method has a drawback that it be may not globally convergent when the objective function is non-convex.Powell[6]suggested that the parameterβkis negative in the PRP method and definedGilbert and Nocedal[7]considered Powell’s suggestion,and proved the globalconvergence ofthe modified PRP method(i.e.,PRP+method) for non-convex functions under the appropriate line search.The convergence properties of LS method have also been studied extensively(see[8-10]).However,the convergence of LS method has not been solved completely under the Wolfe-type line search.

Due to solve the weak convergence of LS method under the Wolfe-type line search,we give a new descent gradient method based on the LS method.And the parameterβksatisfies

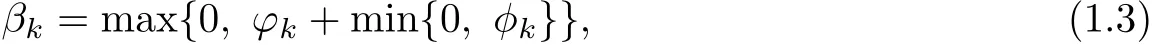
In the next section,we give the corresponding algorithm and prove the suffi cient descent property ofthe new descent method without any line search.In section 3,the globalconvergence of the new method is given under the strong Wolfe line search.In section 4,numerical results are reported.

§2. The Suffi cient Descent Property

In this section,we firstly give the specific algorithm.Then the nice property ofthe presented algorithm is proved,which plays a prominent role in the proof of global convergence.

Algorithm 2.1

Step 1 Data x1∈Rn,ε≥0,δ=0.01,σ=0.1.Set d1=−g1,if||g1||≤ε,then stop.

Step 2 Computeαkby the strong Wolfe line search

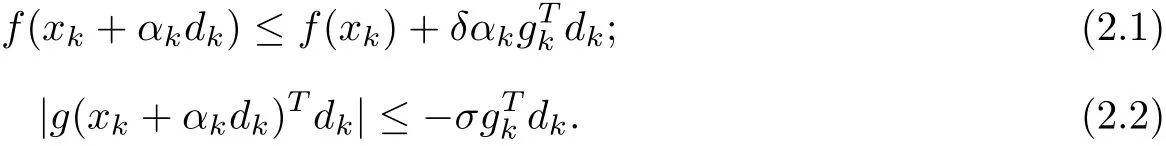
Step 3 Let xk+1=xk+αkdk,gk+1=g(xk+1),if||gk+1||≤ε,then stop.

Step 4 Computeβk+1by(1.3)and generate dk+1by(1.2).

Step 5 Set k=k+1,go to step 2.

Lemma 2.1 Let the sequences{gk}and{dk}be generated by Algorithm 2.1,then

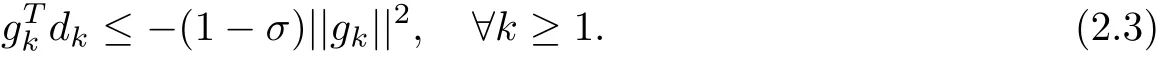
Proof The conclusion can be proved by induction.Since gT1d1=−||g1||2,the conclusion holds for n=1.Now we assume that the conclusion holds for n=k−1,for k≥2 and gk/=0. We need to prove that the result holds for n=k.Multiplying(1.2)by gTk,we have

From(2.4),we get

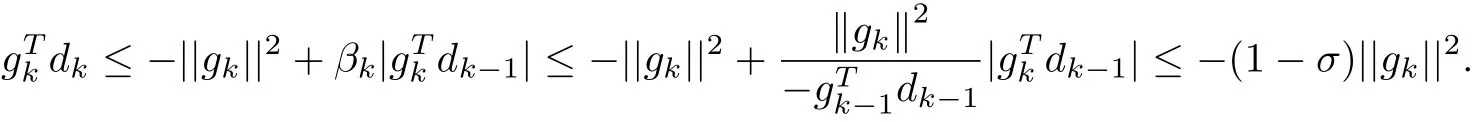
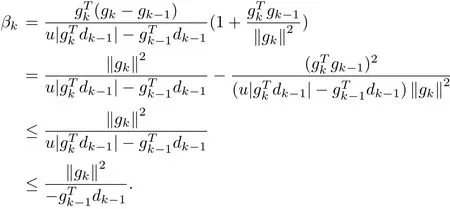
Obviously,the conclusion(2.3)also holds.Therefore,the conclusion(2.3)holds for k.

§3.Global Convergence

In this paper,we prove the global convergence of the new method under the following Assumption(H)

(i)The level setΩ={x∈Rn|f(x)≤f(x1)}is bounded,where x1is the starting point.

(ii)In a neighborhood V ofΩ,f is continuously differentiable and its gradient g is Lipschitz continuous,namely,there exists a constant L＞0 such that

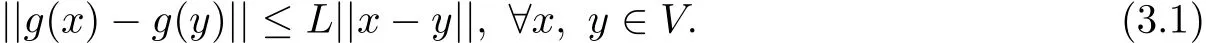
From Assumption(H),there exists a positive constantγ,such that

The conclusion of the following lemma,often called the Zoutendijk condition,is used to prove the global convergence of nonlinear conjugate gradient methods.It was originally given by Zoutendijk[11].Due to that the strong Wolfe line search is a special case of the Wolfe line search,we also get the Zoutendijk condition holds under the general Wolfe line search.

Lemma 3.1 Suppose that Assumption(H)holds.Let the sequences{gk}and{dk}be generated by Algorithm 2.1,then

Lemma 3.2 Suppose that Assumption(H)holds.Let the sequences{gk}and{dk}be generated by Algorithm 2.1.If there exists a positive constant r,such that

Then we have

Proof According to the given condition,(2.3)holds.Then dk/=0,∀k∈N+.

From(1.2),we have

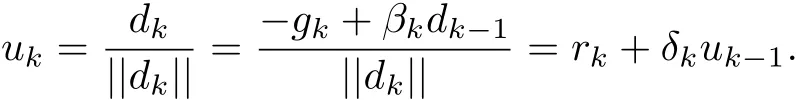
According to the definition of uk,we have||uk||=1,then we have that

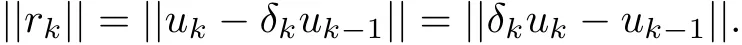
By the definitions ofβkandδk,we haveδk≥0.Then,we obtain that

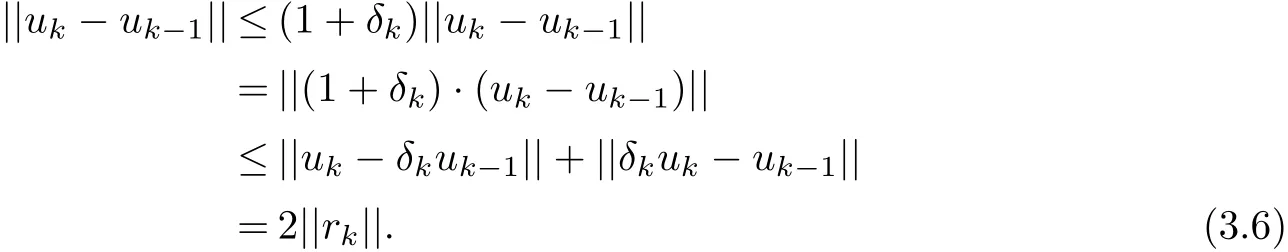
By(2.3),(3.3)～(3.4)and(3.6),we have that

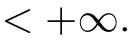
Theorem 3.1 Suppose that Assumption(H)holds.Let the sequences{gk}and{dk}be generated by Algorithm 2.1.Then we have

Proof The conclusion(3.7)willbe proved by contradiction.Suppose that(3.7)does not hold,then(3.4)holds.

By the triangle inequality,we have

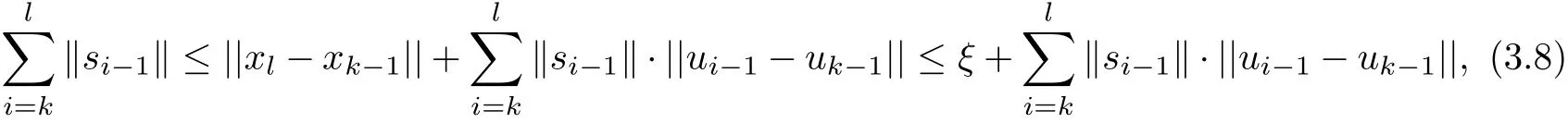
whereξis the diameter ofΩ,i.e.,ξ=max{||x−y||:∀x,y∈Ω}.By(1.3),(2.3),(3.1)～(3.2) and(3.4),we have

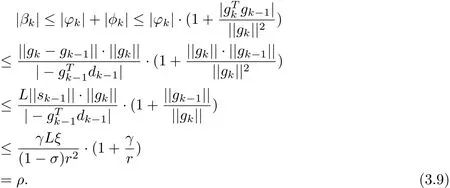
LetΔbe a large enough positive integer such that

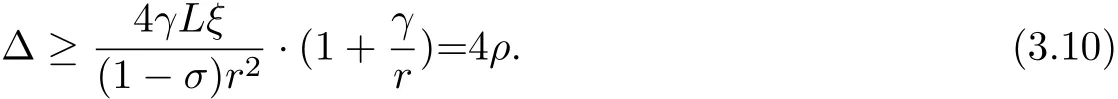
According to(3.5),the seriesis convergent,then there exits a k0large enough such that

For∀i∈[k+1,k+Δ],by the Cauchy-Schwarz inequality and(3.10),we have

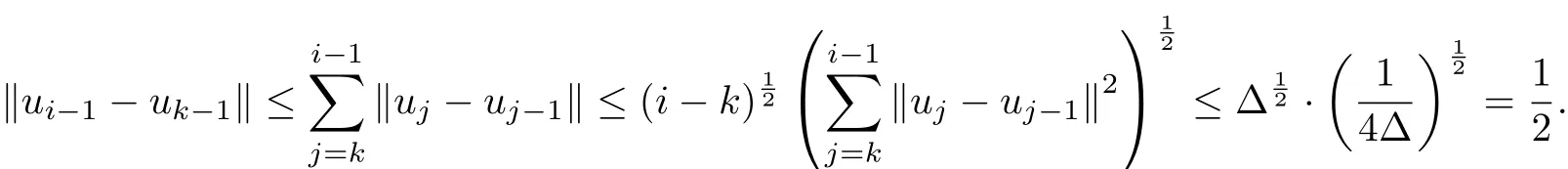
Combining this inequality and(3.8),we have

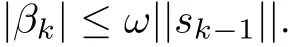
Define Si=2ω2||si||2.By(1.2)and(3.2),for∀l≥k0+1,we have

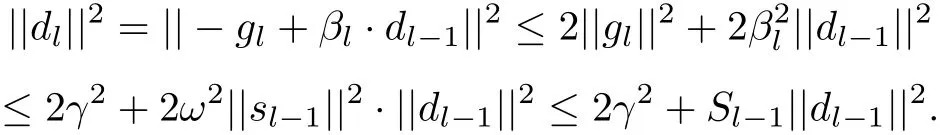
From the above inequality,we have

By the above inequality,the product is defined to be one whenever the index range is vacuous.Let us consider a product of consecutive Si,where k≥k0.Combining(3.10)and (3.12),by the arithmetic-geometric mean inequality,we have

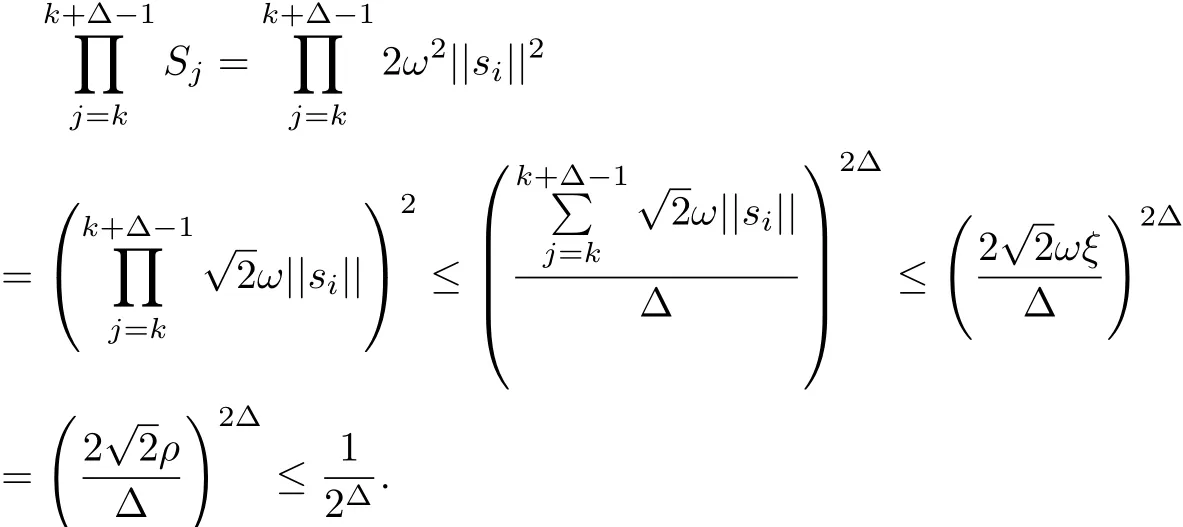
Then,we have that

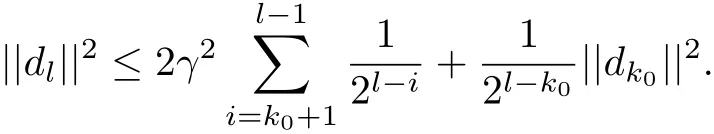
From(2.3),(3.3)～(3.4),we have

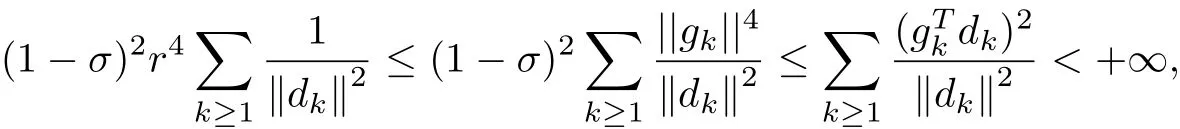
which contradicts(3.14).Hence,we have that

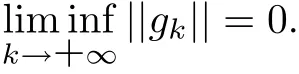
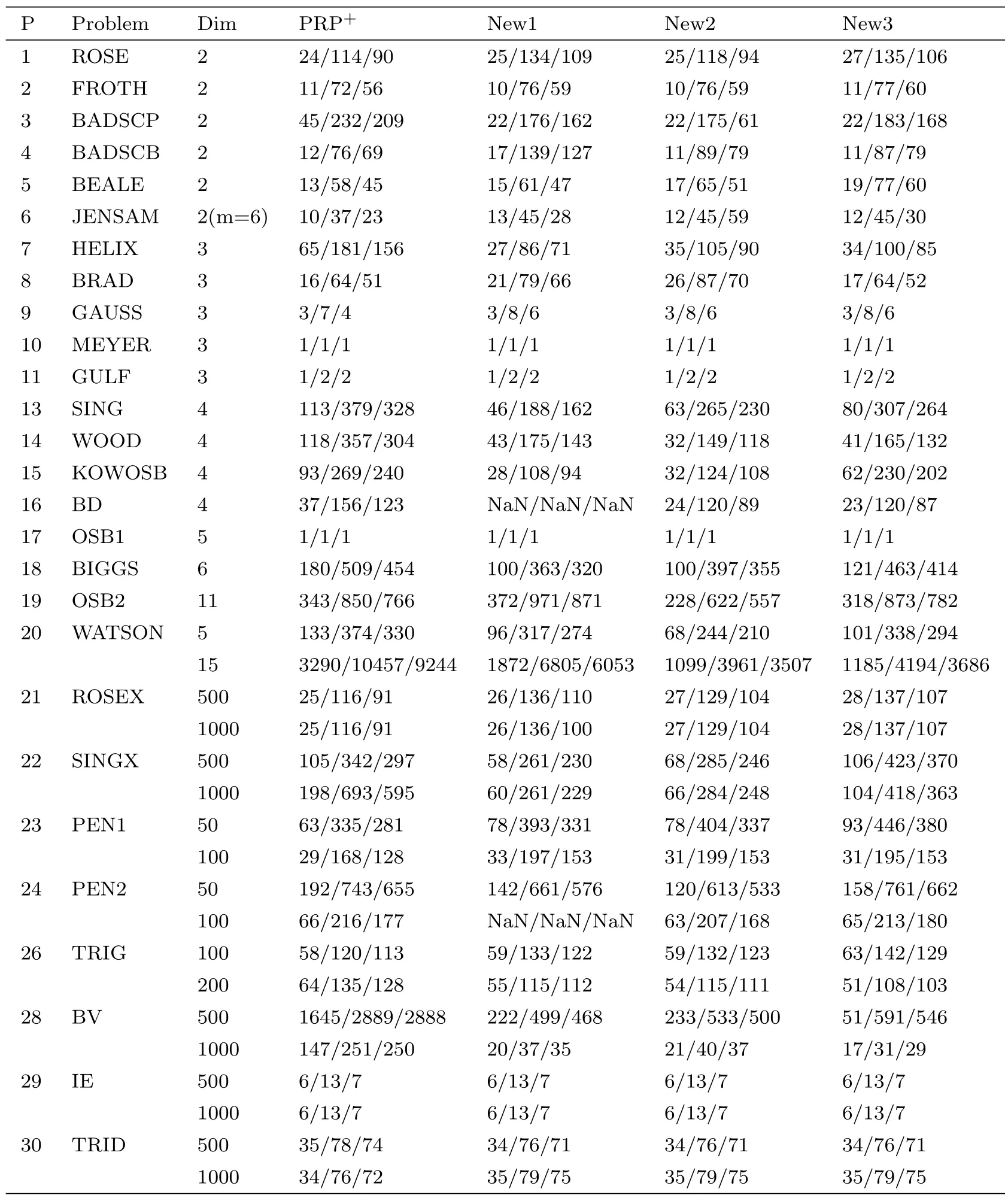
Tabel 1 The Numerical Results of PRP+Method and New Methods

§4.Numerical Results

In this section,we test Algorithm 2.1 on the unconstrained problems in[12]and compare its performance to that of the PRP+method under the strong Wolfe line search conditions.We stop the iteration if the iteration number exceeds 9999 or the inequity||gk||≤ 10−6is satisfied.All codes were written in MATLAB 7.0n a PC with 2.0GHz CPU processor and 512 MB memory and Windows XP operation system.

In Algorithm 2.1,we select the parameter u=0,u=0.2 and u=1 and the corresponding methods are denoted as New1 method,New2 method and New3 method,respectively.

The numericalresults ofour tests are reported in Table 1.The column“Problem”represents the problem’s name in[12].The detailed numerical results are listed in the form NI/NF/NG, where NI,NF,NG denote the number of iterations,function evaluations and gradient evaluations respectively.“Dim”denotes the dimension of the test problems.“NaN”means the calculation failure.

In order to rank the average performance of allabove conjugate gradient methods,one can compute the total number of function and gradient evaluation by the formula

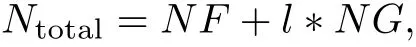
where l is some integer.According to the results on automatic differentiation[13-14],the value of l can be set to 5,i.e.,

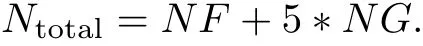
That is to say,one gradient evaluation is equivalent to fi ve function evaluations if automatic differentiation is used.

We compare new methods with PRP+method as follows:for the i th problem,compute the total numbers of function evaluations and gradient evaluations required by new methods and PRP+method by the above formula and denote them by Ntotal,i(New j)and Ntotal,i(PRP+), j=1,2,3.Then we calculate the ratio

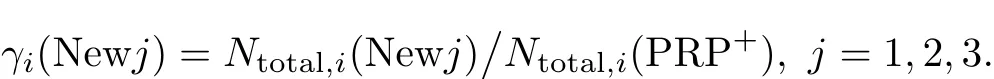
If the i0th problem is not run by the method,we use a constantλ=max{γi(method)|i∈S1} instead ofγi0(method),where S1denotes the set of the test problems which can be run by the method.

The geometric mean ofthese ratios for new methods over allthe test problems is defined by

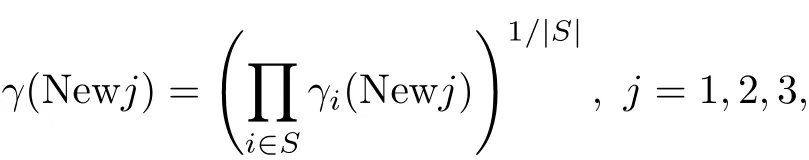
where S denotes the set of the test problems,and|S|denotes the number of elements in S.One advantage of the above rule is that,the comparison is relative and hence does not be dominated by a few problems for which the method requires a great dealoffunction evaluations and gradient functions.According to the above method,we can obtain Table 2 and the results shows that average performance of new methods is much better than the PRP+method,which means that the effi ciency of the new methods is encouraging.

Acknowledgments The author wishes to express their heartfelt thanks to the referees for their detailed and helpful suggestions for revising the manuscript.

Table 2 The Relative Effi ciency of PRP+Method and New Methods

[1]LIU Yu,STOREY C.Effi cient generalized conjugate gradient algorithms,Part 1:theory[J].Journal of Optimization Theory and Application,1992,69:129-137.

[2]POLAK E,RIBIRE G.Note convergence de directions conjugees[J].Revue Fran¸caise d’Informatique et de Recherche Op´erationnelle,1969,16:35-43.

[3]POLAK B T.The conjugate gradient method in extreme problems[J].USSR Comput Math Math Phys, 1969,9:94-112.

[4]HAGER W W,ZHANG Hong-chao.A survey of nonlinear conjugate gradient methods[J].Pacifi c Journal of Optimization,2006,2:35-58.

[5]POWELL M J D.Nonconvex minimization calculations and the conjugate gradient method[R].Berlin: Springer,Germany,1984:122-141.

[6]POWELL M J D.Convergence properties of algorithms for nonlinear optimization[J].SIAM Review,1986, 28:487-500.

[7]GILBERT J C,NOCEDAL J.Global convergence properties of conjugate gradient methods for optimization[J].SIAM Journal on Optimization,1992,2:21-42.

[8]LI Zheng-feng,CHEN Jing,DENG Nai-yang.A new conjugate gradient method and its global convergence properties[J].Systems Science and Mathematical Sciences,1998,11(1):53-60.

[9]YU Gao-hang,ZHAO Yan-lin,WEI Zeng-xin.A descent nonlinear conjugate gradient method for large-scale unconstrained optimization[J].Applied Mathematics and Computation,2007,187:636-643.

[10]LIU Jin-kui,DU Xiang-lin,WANG Kai-rong.Convergence of Descent Methods with Variable Parameters[J]. J ACTA MATHEMATICAE APPLICATAE SINICA,2010,33:222-232.

[11]ZOUTENDIJK G.Nonlinear Programming,Computational Methods[M].Abaclce:North-Holland,1970: 37-86.

[12]MORE J J,GARBOW B S,HILLSTROME K E.Testing unconstrained optimization software[J].ACM Trains Math Software 1981,7:17-41.

[13]DAI Yu-hong,NI Qin.Testing diff erent conjugate gradient methods for large-scale unconstrained optimization[J].Journal of Computational Mathematics,2003,213:11-320.

[14]GRIEWANK A.On Automatic Differentiation[M].Argonne Illinois:Kluwer Academic Publishers,1989: 84-108.

tion:65K,90C

1002–0462(2014)01–0142–09

Chin.Quart.J.of Math. 2014,29(1):142—150

date:2013-08-07

Supported by The Youth Project Foundation of Chongqing Three Gorges University(13QN17);Supported by the Fund of Scientific Research in Southeast University(the Support Project of Fundamental Research)

Biography:LIU Jin-kui(1982-),male,native of Anyang,Henan,a lecturer of Chongqing Three Gorges University,Master,engages in optimization theory and applications.

CLC number:O221.2 Document code:A