A Local Characterization of Lie Homomorphisms of Nest Algebras

YANG Miao-xia,ZHANG Jian-hua

(1.Xianyang Vocational Technical College,Xianyang 712000,China;2.College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062,China)

A Local Characterization of Lie Homomorphisms of Nest Algebras

YANG Miao-xia1,ZHANG Jian-hua2

(1.Xianyang Vocational Technical College,Xianyang 712000,China;2.College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062,China)

In this paper,linear maps preserving Lie products at zero points on nest algebras are studied.It is proved that every linear map preserving Lie products at zero points on any finite nest algebra is a Lie homomorphism.As an application,the form of a linear bijection preserving Lie products at zero points between two finite nest algebras is obtained.

nest algebra;Lie product;Lie homomorphism

§1. Introduction

Let A,B be algebras andϕ:A→B be a linear map.Ifϕ([A,B])=[ϕ(A),ϕ(B)]holds for all A,B∈A,thenϕis called a Lie homomorphism of A,where[A,B]=AB−B A is the Lie product of A and B.Ifϕ([A,B])=[ϕ(A),ϕ(B)]holds for all A,B∈A with AB=0,thenϕ is called a map preserving Lie products at zero points.It is clear that every Lie homomorphism is a map preserving Lie products at zero points.

Recently,many researcher have considered various maps on rings or algebras which determined by zero points.For example,derivable maps at zero points[12],Jordan derivable maps at zero points[35],Lie derivable maps at zero points[68]and maps preserving Jordan products at zero points[9].In this paper,we willconsider maps on nest algebras preserving Lie products at zero points.

Let H be a complex separable Hilbert space and B(H)denote the algebra of all bounded linear operators on H.A nest N is a totally ordered family of orthogonalprojections in B(H) which is closed in the strong operator topology,and which includes 0 and I.The nest algebra associated to a nest N,denoted byτ(N),is the set

If N is a finite nest,thenτ(N)is called a finite nest algebra.Let D(N)be the diagonalofτ(N), and R(N)denote the norm closed algebra generated by{P T(I−P):T∈B(H),P∈N}.It is easy to verify thatτ(N)=D(N)+R(N)if N is a finite nest.

§2.Main Results

In this note,we willprove the following theorem.

Theorem 2.1 Letτ(N)be a finite nest algebra and B be any complex associative algebra andϕ:τ(N)→B be a linear map.Ifϕ([A,B])=[ϕ(A),ϕ(B)]holds for all A,B∈τ(N)with AB=0,thenϕis a Lie homomorphism.

To prove Theorem 2.1,we need some lemmas.We assume thatϕ:τ(N)→B is a linear maps satisfyingϕ([A,B])=[ϕ(A),ϕ(B)]for all A,B∈τ(N)with AB=0.

Lemma 2.1 ϕ([E,F])=[ϕ(E),ϕ(F)]−[ϕ(I),ϕ(E F)]for every idempotent E,F∈τ(N).

Proof From E(F−E F)=0,we haveϕ([E,F−E F])=[ϕ(E),ϕ(F−E F)].That is,

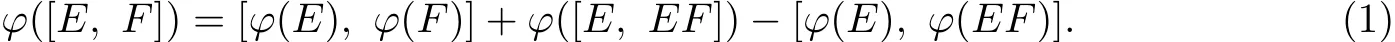
From(E−I)E F=0,we haveϕ([E−I,E F])=[ϕ(E−I),ϕ(E F)].Thus,

By(1)and(2),then for every idempotent E,F∈τ(N),

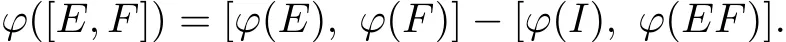
The proof is completed.

Lemma 2.2 ϕ([E,F])=[ϕ(E),ϕ(F)]−[ϕ(E F),ϕ(I)]for every idempotent E,F∈τ(N).

Proof From(E−E F)F=0,we haveϕ([E−E F,F])=[ϕ(E−E F),ϕ(F)].That is,

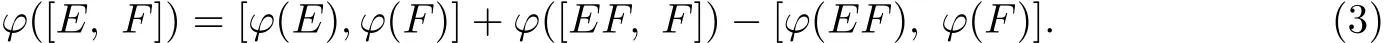
It follows from E F(F−I)=0 thatϕ([E F,F−I])=[ϕ(E F),ϕ(F−I)].Thus,

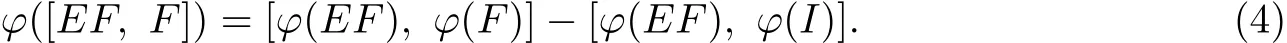
By(3)and(4),thenϕ([E,F])=[ϕ(E),ϕ(F)]−[ϕ(E F),ϕ(I)]for every idempotent E,F∈τ(N).The proof is completed.

Lemma 2.3 ϕ([E,F])=[ϕ(E),ϕ(F)]for every idempotent E,F∈τ(N).

Proof By Lemmas 2.1 and 2.2,then for every idempotent E,F∈τ(N),

and

It follows that

and so[ϕ(I),ϕ(E F)]=0.Henceϕ([E,F])=[ϕ(E),ϕ(F)]for every idempotent E,F∈τ(N). The proof is completed.

Proof of Theorem 2.1 Let N={0=P0＜P1＜···＜Pn=I}be a finite nest and Ek=Pk−Pk−1(k=1,2,···,n).ThenEkand so every operator of D(N)is a finite linear combination ofidempotents in D(N).Hence by Lemma 2.3,we have for every D1,D2∈D(N),

For each P,Q∈N and T,S∈B(H),write E=P+P T P⊥,F=Q+QS Q⊥.Then E,F are idempotents ofτ(N).It follows from Lemma 2.3 that

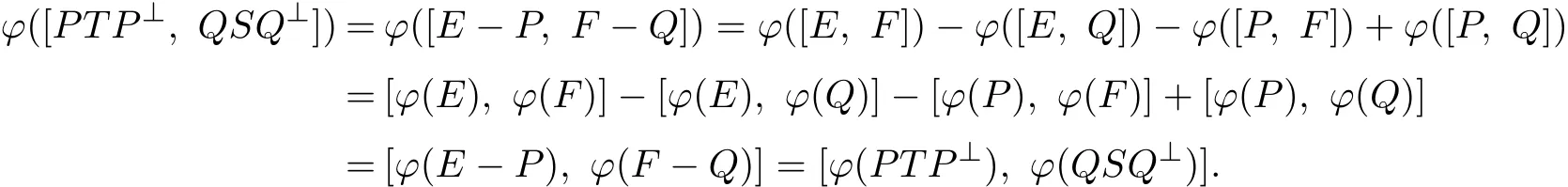
This implies that for every R1,R2∈R(N),

Similarly,we can show that

for every D∈D(N)and R∈R(N).

For each A,B∈τ(N),sinceτ(N)=D(N)+R(N),there exist D1,D2∈D(N)and R1,R2∈R(N)such that A=D1+R1,B=D2+R2.Then by(5),(6)and(7)

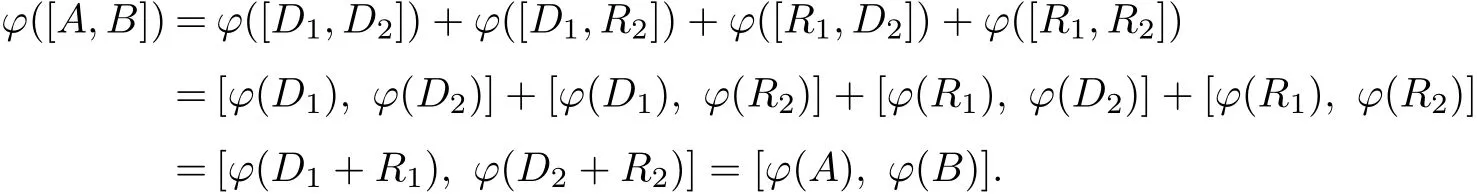
Henceϕis a Lie homomorphism.The proof is completed.

From Theorem 2.1 and the result of[10],we have the following corollary.

Corollary 2.1 Let N and M be two finite nest andϕ:τ(N)→ τ(M)be a linear bijective map.Ifϕ([A,B])=[ϕ(A),ϕ(B)]holds for all A,B∈τ(N)with AB=0,then there exist an invertible operator T∈B(H)and a linear functional f:τ(N)→ℂsuch that either ϕ(A)=T AT−1+f(A)I for all A∈τ(N),orϕ(A)=−T J A∗J T−1+f(A)I for all A∈τ(N), where J is an involution.

[1]AN Run-ling,HOU Jin-chuan.Characterizations of derivations on triangular rings:Additive maps derivable at idempotents[J].Linear Algebra Appl,2009,431:1070–1080.

[2]AN Run-ling,HOU Jin-chuan.Characterizations of Jordan derivations on rings with idempotents Additive maps Jordan derivable at zero[J].Chinese Journal of Contemporary Mathematics,2010,31(A):463–474.

[3]BREˇsAR M.Characterizing homomorphisms,multipliers and derivations in rings with idempotents[J].Proc Roy Soc Edinburgh Sect,2007,137:9–21.

[4]JIAO Mei-yan,HOU Jin-chuan.Additive maps derivable at zero points on nest algebras[J].Linear Algebra Appl,2010,432:2984–2994.

[5]ZHAO Jin-ping,ZHU Jun.Jordan higher all-derivable points in triangular algebras[J].Linear Algebra Appl, 2012,436:3072–3086.

[6]LU Fang-yan,JING Wu.Characterizations of Lie derivations of B(X)[J].Linear Algebra Appl,2010,432: 89–99.

[7]JI Pei-sheng,QI Wei-qing.Characterizations of Lie derivations of triangular algebras[J].Linear Algebra Appl,2011,435:1137–1146.

[8]QI Xiao-fei,CUI Jian-lian,HOU Jin-chuan.Characterizing additiveξ-Lie derivations of prime algebras by ξ-Lie zero products[J].Linear Algebra Appl,2011,434:669–682.

[9]ZHANG Xiao-hui,ZHANG Jian-hua.Characterizations of Jordan isomorphism of nest algebras[J].Acta Math Sinica(Chinese Series),2013,56:553–560.

[10]MARCOUX L W,SSOUROUR A R.Lie isomorphisms ofnest algebras[J].J Funct Anal,1999,164:163–180.

tion:46L35

1002–0462(2014)01–0125–04

Chin.Quart.J.of Math. 2014,29(1):125—128

date:2013-07-15

Supported by the Specialized Research Foundation for the Doctoral Program of Universities and Colleges of China(20110202110002)

Biographies:YANGMiao-xia(1964-),female,native of Xianyang,Shaanxi,a lecturer of Xianyang Vocational Technical College,M.S.D.,engages in functional analysis;ZHANG Jian-hua(1965-),male,native of Yongcheng, Henan,a professor of Shaanxi Normal University,Ph.D.,engages in operator algebra.

CLC number:O177.1 Document code:A