A Stage-structured Predator-prey Model with Time Delay and Impulsive Eff ects

DU Yan-ke,Wu Xiang-dong,Xu Rui

(1.Institute of Applied Mathematics,Shijiazhuang Mechanical Engineering College,Shijiazhuang 050003, China;2.Department of Guns Engineering,Shijiazhuang Mechanical Engineering College,Shijiazhuang 050003,China)

A Stage-structured Predator-prey Model with Time Delay and Impulsive Eff ects

DU Yan-ke1,Wu Xiang-dong2,Xu Rui1

(1.Institute of Applied Mathematics,Shijiazhuang Mechanical Engineering College,Shijiazhuang 050003, China;2.Department of Guns Engineering,Shijiazhuang Mechanical Engineering College,Shijiazhuang 050003,China)

A delayed predator-prey model concerning impulsive spraying pesticides and releasing natural enemies is proposed and investigated,in which both the prey and the predator have a history that takes them through two stages:immature and mature.The global attractiveness of the pest-eradication periodic solution is discussed,and suffi cient condition is obtained for the permanence of the system.Further,numerical simulations show that there is a characteristic sequence of bifurcations leading to a chaotic dynamics, which implies that the system with constant periodic impulsive perturbations admits rich and complex dynamics.

stage-structure;delay;biological and chemical control;impulsive eff ect;global attractiveness;permanence

§1. Introduction

Pest outbreaks often cause serious ecologicaland economic problems.A wide range of pest control strategies is available to farmers such as biological,chemical,cultural and physical treatments.For example,farmers often catch the pests by mechanical tools or poison them by the use of pesticides.However,eradication for the pests is diffi cult both practically and economically as the pests can breed quickly.Another way is biological control which uses natural enemies such as predators and parasites to suppress a pest population.One approachto biological control is augmentation,which is manipulation of existing natural enemies to increase their effectiveness.This can be achieved by mass production or migration from other areas,and periodic release of natural enemies of the pests.Whenever possible,different pest control techniques should work together rather than against each other.In some cases,this can lead to synergy.We’ll intend to describe the above processes by impulsive diff erential equations,which have been recently used in population ecology(see,for example,[1-3]).At the same time,it is practical for us to introduce the stage structure in the models that embody the distinction among diff erent stages in the pest and the natural enemy individuals,as well as the delay describing the gestation period and the maturity period.Whereas,most of the researchers consider models with stage structure only for one species and merely impulsively chemical or biological control(see,for instance,[4-7]).It is of importance to discuss effects of stage structure for both the prey and the predator species,and periodic releasing natural enemies and spraying pesticides(or harvesting pest)at diff erent fixed times on pest control.To this end,in the present paper,we propose the following diff erential equations with time delay, stage structure and impulses

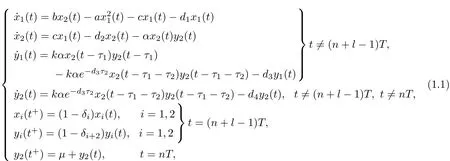
where x1(t)and x2(t)denote the densities of the immature and the mature prey(pest)population at time t,respectively,y1(t)and y2(t)denote the densities of the immature and the mature predator(natural enemy)population at time t.All coeffi cients are positive constants, and 0＜l≤1,0＜δi＜1(i=1,2,3,4).The model is derived as follows.b is the birth rate for the mature prey;c is the proportion that the immature prey population become the mature;a is the intra-specific competition rate of the immature prey.di(i=1,2,3,4)are the death rates ofthe immature and the mature prey,the immature and the mature predator,respectively;αis the capturing rate ofmature predator;k(τ1)is the rate(constant time)ofconversion ofnutrients into the reproduction of the mature predator;τ2is the length of the immature predator stage. δi(i=1,2,3,4)represent the fractions of the immature and the mature prey,the immature and the mature predator,respectively,which die due to the pesticides at t=(n+l−1)T;µis the release amount of the mature predator at t=nT;T is the period of the impulsive eff ects, n∈Z+and Z+={1,2,···}.

The organization ofthis paper is as follows.A fundamentaldefinition and some lemmas are given in Section 2.In Section 3,we derive suffi cient condition for the global attractiveness of the pest-eradication periodic solution.In Section 4,we discuss the uniform permanence of the system.In Section 5,numerical simulations are carried out to illustrate our main results andshow that the system can exhibit many new phenomena and a brief discussion is given.

§2. Preliminaries

The following definition and lemmas are useful in proving our main results.

Defi nition 2.1 System(1.1)is said to be permanent if there are constants m,M ＞0(independent ofinitialvalues)and a finite time T0such that for allsolutions(x1(t),x2(t),y1(t), y2(t))with all initial values x1(0+)＞ 0,x2(0+)＞ 0,y1(0+)＞ 0,y2(0+)＞ 0,m ≤x1(t),x2(t),y1(t),y2(t)≤ M holds for all t≥ T0.Here,T0may depend on the initial values(x1(0+),x2(0+),y1(0+),y2(0+)).

Lemma 2.1 Suppose that(x1(t),x2(t),y1(t),y2(t))is a solution of system(1.1)with initial values xi(0+)≥ 0,yi(0+)≥ 0,then xi(t)≥ 0,yi(t)≥0 for all t≥0.And further xi(t)＞0,yi(t)＞0 if xi(0+)＞0,yi(0+)＞0(i=1,2).

Lemma 2.2[8]Let the function m∈P C1[R+,R]satisfy the inequalities

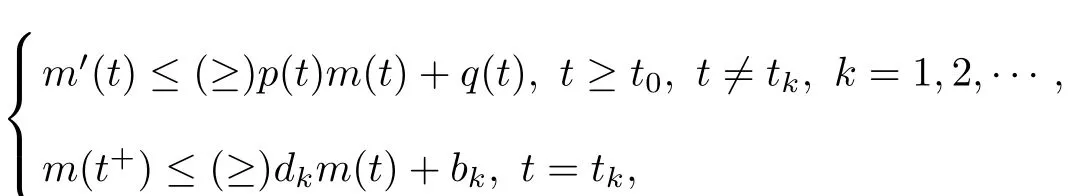
where p,q∈P C[R+,R]and dk≥0,bkare constants.Then for all t≥t0,

Lemma 2.3 There exists a constant M ＞0 such that xi(t)≤M,yi(t)≤M(i=1,2) for each solution(x1(t),x2(t),y1(t),y2(t))of system(1.1)for all t suffi ciently large.

Proof Define

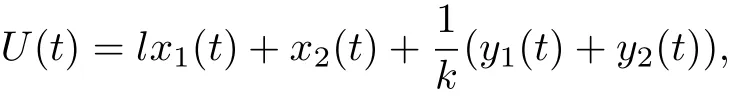
where 0＜l＜d2/b is a constant.

Letλ=min{d2−lb,d3,d4}.When t/=nT,we have

where M0=(lλ+c−lc−ld1)2/(4la).

When t=nT,U(nT+)=U(nT)+µ/k.By Lemma 2.2,for t∈(nT,(n+1)T],we have

Hence,U(t)is uniformly ultimately bounded,and there exists a constant M ＞0 such that xi(t)≤M,yi(t)≤M(i=1,2)for each solution(x1(t),x2(t),y1(t),y2(t))of system(1.1)for all t suffi ciently large.The proof is complete.

By use of the discrete dynamical system determined by the stroboscopic map,we can easily derive the following lemma.

Lemma 2.4 Let us consider the following scalar impulsive diff erential equations

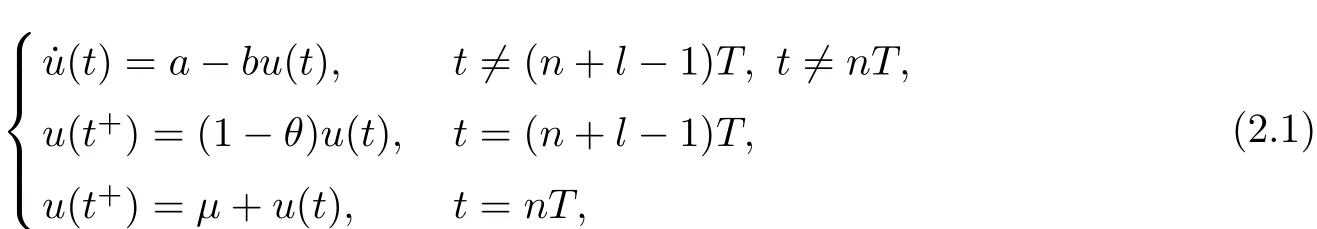
where a≥0,b＞0,0＜θ＜1,µ≥0.Then system(2.1)has a unique positive periodic solution

which is globally asymptotically stable,where

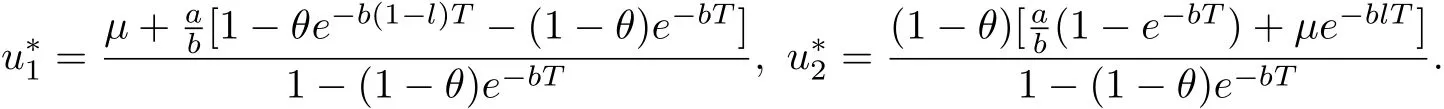
Obviously,

where u∗=a(1−θ)(1−e−bT)/[b(1−(1−θ)e−bT)].

§3. Extinction

Obviously,there exists a pest-eradication periodic solution of system(1.1)

It is easy to show that

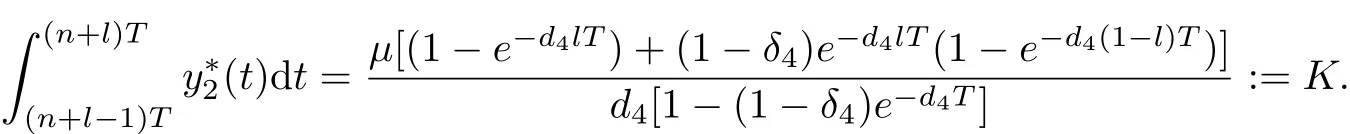
Denote

whereδmin=min{δ1,δ2},σis a suffi ciently smallpositive constant satisfying that l1＞0.

Theorem 3.1 If the following assumption holds

then the pest-eradication periodic solutionof system(1.1)is globally attractive.

Proof By the expression of l1,forε＞0 suffi ciently small,we derive that

Noting that˙y2(t)≥−d4y2(t),t/=(n+l−1)T,t/=nT,by comparison theorem of impulsive equation,we have

for all t suffi ciently large.

Define

Then,we derive from(3.1)and(3.2)that

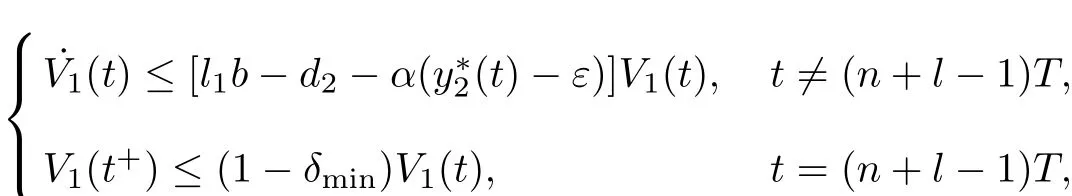
which leads to

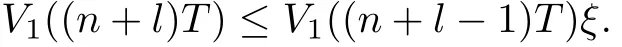
Furthermore,V1((n+l)T)≤V1(lT)ξnand V1((n+l)T)→0 as n→∞.Hence,x1(t)→0, x2(t)→0 as n→∞since 0＜V1(t)≤V1((n+l−1)T)(1−δmin)exp(l1bT)for(n+l−1)T＜t≤(n+l)T.It follows that forε＞0 suffi ciently small,there must exist a T′＞0 such that 0＜xi(t)＜ε,i=1,2,t≥T′.Then,we get

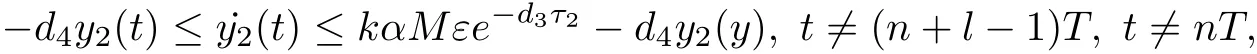
again from Lemma 2.4 and by comparison,we obtain that

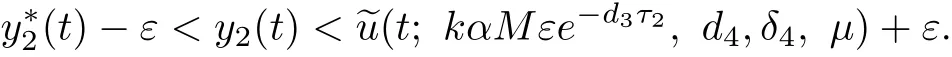
§4.Permanence

In this section,we discuss the permanence of system(1.1).

Denote

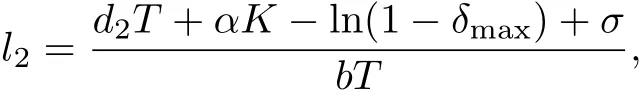
whereδmax=max{δ1,δ2}.

Theorem 4.1 System(1.1)is permanent provided that the following assumption holds

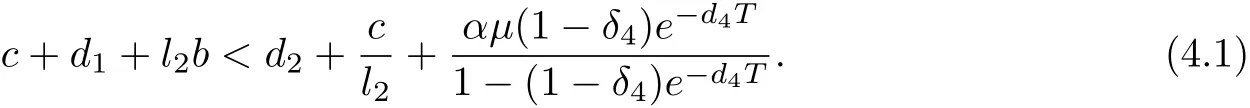
Proof From(3.2),we obtain that

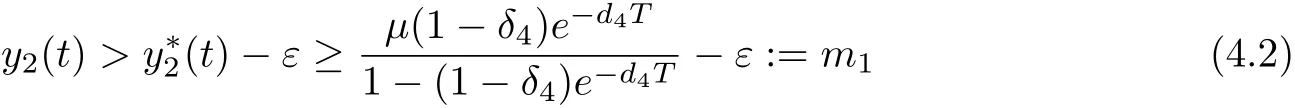
for t suffi ciently large.Combining with Lemma 2.3,we only need to find a constant m＞0 such that xi(t)≥m(i=1,2),y1(t)≥m for t suffi ciently large.

By(4.1)and the expression of l2,we can choose m2＞0,ε＞0 suffi ciently small such that

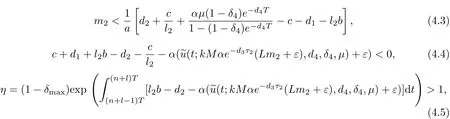
where L=c(1−e−(d2+αm1)T)/[(d2+αm1)(1−(1−δ2)e−(d2+αm1)T)].

We now claim that for arbitrary t0＞0,x1(t)＜m2can not hold for all t≥t0.Otherwise, if there exists such a t0such that x1(t)＜m2for all t≥t0,then

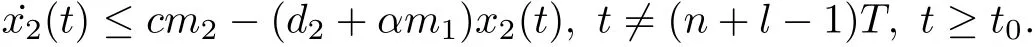
A comparison argument shows that for anyε＞0,there exists asuch that

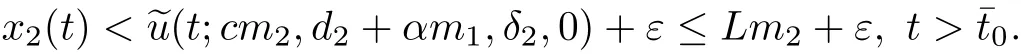
Therefore,

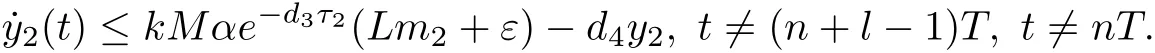
Then,for anyε＞0,there exists asuch that

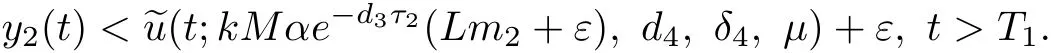
Define

By(4.3),(4.4)and x1(t)＜m2,for t≥T1,we derive that

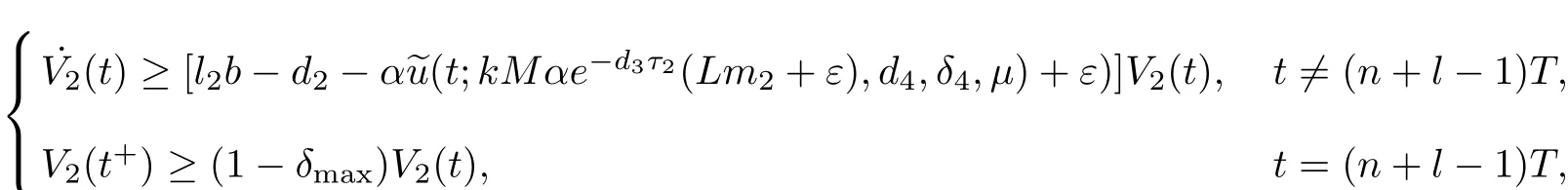
which yields

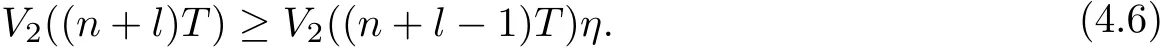
Let N1∈Z+and(N1+l−1)≥T1.From(4.5)and(4.6),we get V2((N1+n+l)T)≥V2((N1+l)T)ηn→∞as n→∞.A contradiction occurs.Therefore,there exists a t1＞0 such that x1(t1)≥m2.

In the following,we are left to consider two cases.If x1(t)≥m2for all t≥t1,this is the expected case.On the other hand,we consider the case that x1(t)oscillates about m2.LetIn the same way,we can obtain a time sequence t1≤t2＜t3＜···＜t2k＜t2k+1＜···,such that

(1)x1(t2k)=m2or x1(t2k)＞m2and(1−δ1)m2＜x1(t+2k)≤m2,k∈Z+;

(2)x1(t2k+1)=m2,k∈Z+;

(3)x1(t)＜m2for t∈(t2k,t2k+1),k∈Z+;

(4)x1(t)＞m2for t∈(t2k+1,t2k+2),k∈Z+.

Using similar arguments as above,we can prove that there must be¯T=sup{t2k+1−t2k,k∈Z+}.

For t≥t1,t∈(t2k,t2k+1),k∈Z+,letting N2=⌈¯T/T⌉(⌈x⌉is the minimum integer being greater than or equalto x),we have that

Then,for anyε＞0 suffi ciently small,any t suffi ciently large,we obtain that

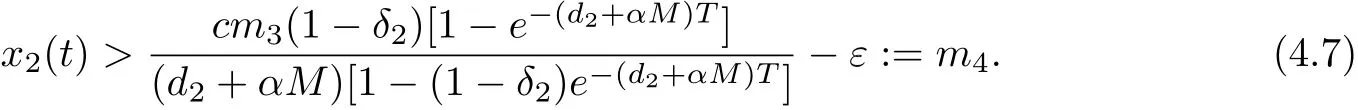
Noting that the third equation of system(1.1)can be rewritten as

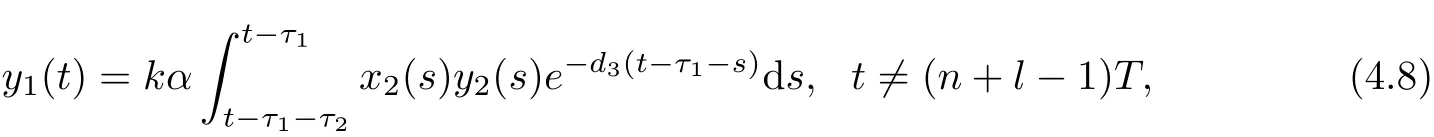
we deduce from(4.2),(4.7)and(4.8)that

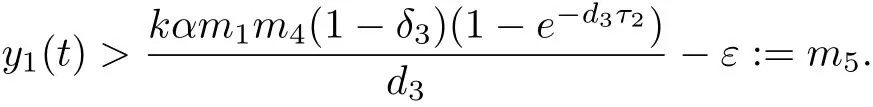
Denote m=min{m1,m3,m4,m5}.Then xi(t)≥m,yi(t)≥m(i=1,2)hold for all t suffi ciently large.The proof is complete.

§5.Numerical Simulations and Discussion

In this section,we first give some examples to illustrate the main theoreticalresults in Sec. 3 and Sec.4 and further exhibit some rich and complex phenomena.At last,a briefdiscussion is given.

In system(1.1),set b=10,a=0.2,c=0.1,α=0.5,k=0.3,d1=0.2,d2=0.3,d3= 0.3,d4=0.2,τ1=0.5,τ2=0.5,l=0.5,T=1,δ1=0.5,δ2=0.5,δ3=0.2,δ4= 0.1,µ=2.Then the condition of Theorem 3.1 holds and the pest-eradication periodic solution (0,0,0,y∗2(t))is globally attractive(see Fig.1).If we choose b=10,a=0.2,c=0.5,α= 0.2,k=0.3,d1=0.1,d2=0.1,d3=0.3,d4=0.2,τ1=1,τ2=1,l=0.5,T=1.5,δ1= 0.4,δ2=0.6,δ3=0.2,δ4=0.3,µ=1,then the condition of Theorem 4.1 holds and system (1.1)is permanent(see Fig.2).Further,the system has rich dynamic behaviors.In Fig.3,we exhibit the bifurcation diagrams when we fix other parameters as those of Fig.2 except that µ=3 and choose T as a bifurcation parameter.We also investigate the effects of the releaseamountµof natural enemies.Fig.4 shows the bifurcation and chaos diagrams for 0＜µ＜12. Fig.3 and Fig.4 clearly show that system(1.1)has rich dynamics including period-doubling bifurcation,periodic halving bifurcation,symmetry-breaking pitchfork bifurcation and chaos.

Fig.1 Dynamic Behavior of System(1.1)with b=10,a=0.2,c=0.1,α=0.5,k=0.3,d1= 0.2,d2=0.3,d3=0.3,d4=0.2,τ1=0.5,τ2=0.5,l=0.5,T=1,δ1=0.5,δ2=0.5,δ3= 0.2,δ4=0.1,µ=2.(a)Time-series of the Immature and the Mature Prey Population Evolving According to the Chemical and Biological Control.(b)Time-series of the Immature and the Mature Predator Population.

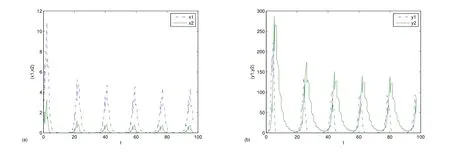
Fig.2 Dynamic Behavior of System(1.1)with b=10,a=0.2,c=0.5,α=0.2,k=0.3,d1= 0.1,d2=0.1,d3=0.3,d4=0.2,τ1=1,τ2=1,l=0.5,T=1.5,δ1=0.4,δ2=0.6,δ3=0.2,δ4=0.3,µ= 1.(a)Time-series of the Immature and the Mature Prey Population Evolving According to the Chemical and Biological Control.(b)Time-series of the Immature and the Mature Predator Population.

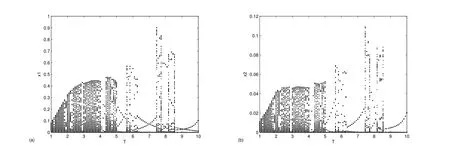
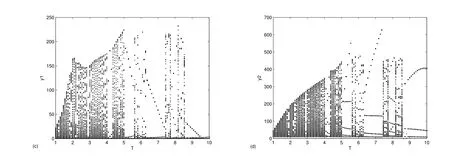
Fig.3 Bifurcation Diagrams of System(1.1)with b=10,a=0.2,c=0.5,α=0.2,k=0.3,d1= 0.1,d2=0.1,d3=0.3,d4=0.2,τ1=1,τ2=1,l=0.5,δ1=0.4,δ2=0.6,δ3=0.2,δ4=0.3,µ=3. These Show the Eff ect of Parameter T on the Dynamic Behavior.(a)x1are Plotted for 100 Values of T over[1,10].(b)x2are Plotted for 100 Values of T over[1,10].(c)y1are Plotted for 100 Values of T over[1,10].(d)y2are Plotted for 100 Values of T over[1,10].

Fig.4 Bifurcation Diagrams of System(1.1)with b=10,a=0.2,c=0.5,α=0.2,k=0.3,d1= 0.1,d2=0.1,d3=0.3,d4=0.2,τ1=1,τ2=1,l=0.5,δ1=0.4,δ2=0.6,δ3=0.2,δ4=0.3,T=3. These Show the Eff ect of Parameterµon the Dynamic Behavior.(a)x1are Plotted for 180 Values ofµover[0,12].(b)x2are Plotted for 180 Values ofµover[0,12].(c)y1are Plotted for 180 Values ofµover[0,12].(d)y2are Plotted for 180 Values ofµover[0,12].

In this paper,we discussed a delayed predator-prey model concerning impulsive spraying pesticides and releasing naturalenemies,in which both the prey and the predator have a history that takes them through two stages:immature and mature.Suffi cient condition is obtained for the global attractiveness of the pest-eradication periodic solution and the permanence of thesystem.It is easily seen that(3.1)holds ifδminis greater than a certain value,which implies that the control strategy can be made to succeed by spraying enough or more toxic pesticides. This discussion can be performed in terms ofother parameters.Our impulsive controlstrategy off ers tactical basis for the practical pest management.

[1]BAEK H,DO Y.Stability for a holling type IV food chain system with impulsive perturbations[J].Kyungpook Mathematical Journal,2008,48:515-527.

[2]GEORGESCU P,MOROSANU G.Impulsive perturbations of a three-trophic prey-dependent food chain system[J].Math Comput Model,2008,48:975-997.

[3]LIU Bing,CHEN Lan-sun,ZHANG Yu-juan.The dynamics of a prey-dependent consumption model concerning impulsive control strategy[J].Appl Math Comput,2005,169:305-320.

[4]JIANG Gui-rong,LU Qi-shao,PENG Lin-ping.Impulsive ecological control of staged-structured pest management system[J].Math Biosci Eng,2005,2:329-344.

[5]PANG Guo-ping,WANG Feng-yan,CHEN Lan-sun.Extinction and permanence in delayed stage-structure predator-prey system with impulsive eff ects[J].Chaos Soliton Fract,2009,39:2216-2224.

[6]SHI Rui-qing,CHEN Lan-sun.Staged-structured Lotka-Volterra predator-prey models for pest management[J].Appl Math Comput,2008,203:258-265.

[7]SONG Xin-yu,HAO Mei-ying,MENG Xin-zhu.A stage-structured predator-prey model with disturbing pulse and time delays[J].Appl Math Model,2009,33:211-223.

[8]LAKSHMIKANTHAM V,BAINOV D,SIMEONOV P.Theory of Impulsive Differential Equations[M]. Singapore:World scientific,1989.

tion:34D05,34K45,93C10

1002–0462(2014)01–0045–10

Chin.Quart.J.of Math. 2014,29(1):45—54

date:2012-04-08

Supported by the NNSF of China(11071254);Supported by the Science Foundation of Mechanical Engineering College(YJJXM11004)

Biography:DU Yan-ke(1977-),female,native of Shenzhou,Hebei,a lecturer of Shijiazhuang Mechanical Engineering College,M.S.D.,engages in diff erential equations and mathematical biology.

CLC number:O175.1 Document code:A