Direct Solutions of Some Singular Integral Equations on the Building Domain of Complex Biballs

GONG Ding-dong,GUO Yu-qin

(1.Department of Mathematical Sciences,Zhejiang Sci-Tech University,Hangzhou 310018,China;2. Library of Zhejiang Sci-Tech University,Hangzhou 310018,China)

Direct Solutions of Some Singular Integral Equations on the Building Domain of Complex Biballs

GONG Ding-dong1,GUO Yu-qin2

(1.Department of Mathematical Sciences,Zhejiang Sci-Tech University,Hangzhou 310018,China;2. Library of Zhejiang Sci-Tech University,Hangzhou 310018,China)

By means of the method of solid angle coeffi cients and the permutation formula on the building domain of complex biballs,direct solutions of some singular integral equations with variable coeffi cients are discussed and the explicit formulas for these solutions are obtained.

the building domain ofcomplex biballs;solid angle coeffi cients;singular integral equations with variable coeffi cients;explicit solutions

§1. Introduction

For singular integrals ofseveralcomplex variables,there are lots ofresearches.Gong Sheng[1]studied the permutation formula and the composition formula,and discussed the singular integraltheory on the complex sphere ofthe unit ball.In 1990s Lin Liangyu[2]used the topological method to establish the discrete holomorphic kernelon the bounded domain,and obtained the integral representations of the diff erential and holomorphic functions on the bounded domain. As applications of this kernel,the singular integral on the building domain of complex biballs has been studied in[3-4].

For the study on the singular integral equations,regularization is an important method, which is to convert the equations into Fredholm equations.Generally speaking,however,the theorems on regularization do not achieve any explicit solutions of equations.

In this paper,the authors use the method of solid angle coeffi cients and Poincar´e-Bertrand permutation formula to study the singular integral equations with variable coeffi cients on the building domain ofcomplex biballs,and discuss direct solutions ofsome singular integralequations,and obtain the explicit formulas for these solutions.These results are the generalization of those on the complex sphere of the unit ball in[1].Here n＞1,for the characteristics of severalcomplex variables all the results may not hold for n=1.

§2. Defi nitions and Propositions

In[3],Lin et al.introduced the concept of the building domain of complex biballs and extended the singular integralon the sphere of the complex unit ball.

Defi nition 1[3]A connected open setis defined as a building domain of complex biballs,whereand B1∩B2/=∅,B1=/B1∩B2/=B2.

Defi nition 2[3]The discrete holomorphic kernelΩ(η(ζ,z))is defined by

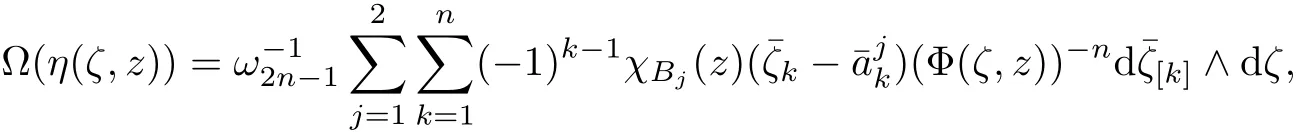
We denote

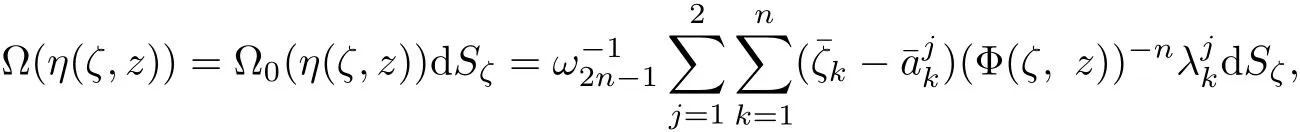
is the complex direction cosine atζon the sphere∂Bj,d Sζis the area element atζ. The boundary∂D can be split into two pieces as follows,

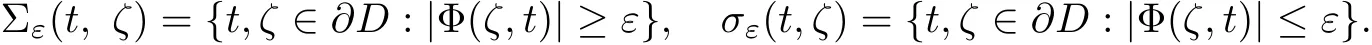
Let Lipαbe the space of functions with H¨older exponentα(0＜α≤1)on∂D and L∗the space of Lipschitz functions on∂D.A contains functions in L∗which are holomorphic in D.

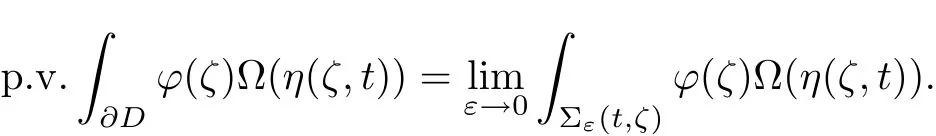
Denoting bε(t)={ζ∈ℂn:|Φ(η(ζ,t))|≤ε},the solid angle coeffi cient(cf.[3])at t∈∂D is

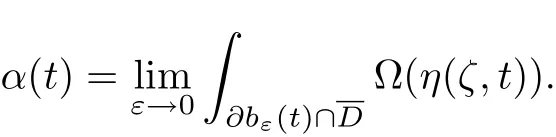
From[3],when t∈∂D0(the smooth part of∂D),,when t∈/∂D0,0＜α(t)＜1.

Proposition 1(Poincar´e-Bertrand Formula)[4]Letϕ(ζ,ξ)∈Lipα,t∈∂D,then

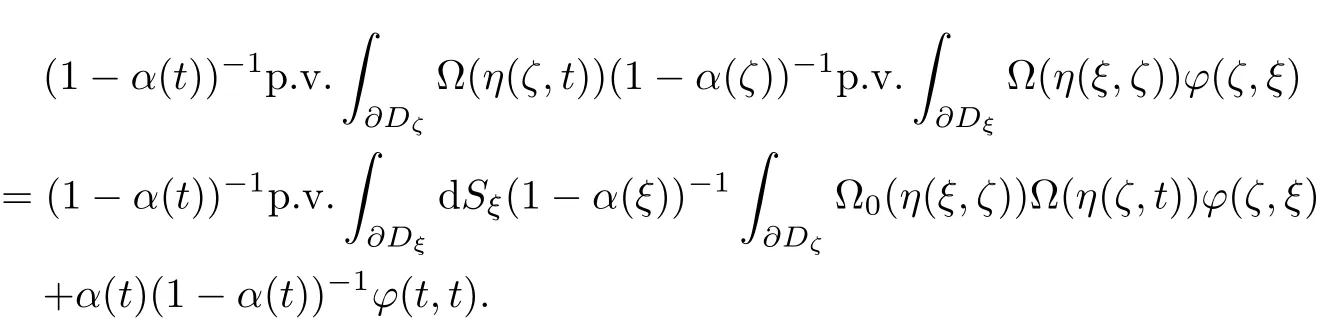
Gong[1]considered the following singular integral equations on the ball B,

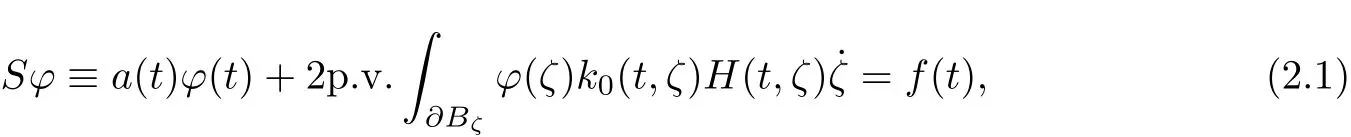
Proposition 2(cf.Theorem 2.15.3 in[1]) If a(t)and k0(t,ζ)∈A,b(t)=k0(t,t), when a2(t)−b2(t)never vanishes on∂B,then(2.1)has a unique solution

in L∗,the operator T is defined by,forψ∈L∗,

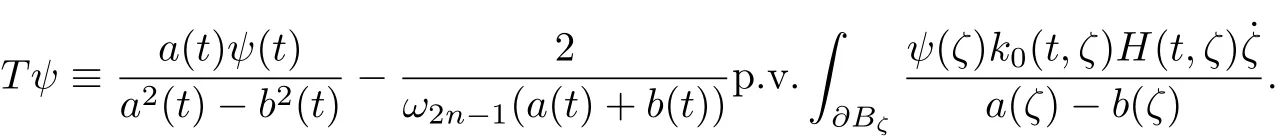
§3. Direct Solutions of the Singular Integral Equations with Variable Coeffi cients

We consider the following singular integral equations on the boundary,

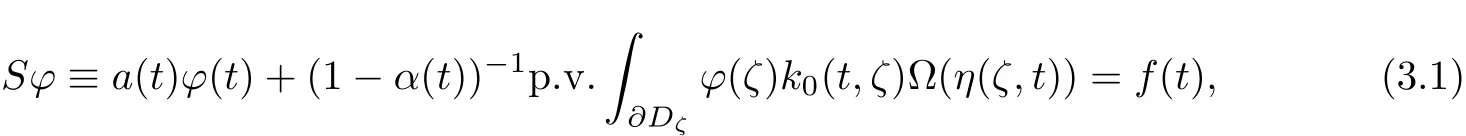
where a(t),f(t),k0(t,ζ)∈L∗,t∈∂D.

In the following Theorem 3.4,we try to show that,on certain conditions,the equation(3.1) can be solved directly.We need the following lemmas.

Lemma 3.1 Let f(t,ζ,ξ)∈L∗and f(t,ζ,ξ)in A as a function ofζ,then

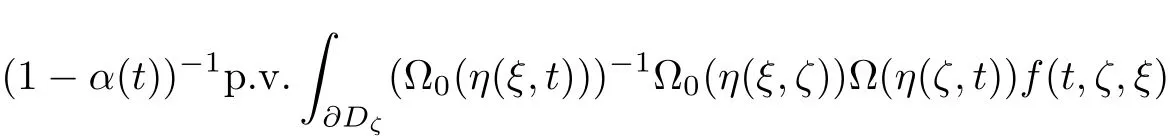
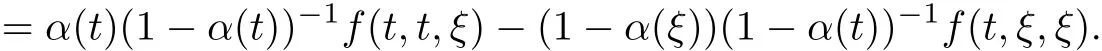
The proof of this lemma is similar to that of Lemma 1 in[12],so we omit the details.

Lemma 3.2 Letϕ1(t,ζ)andϕ2(t,ζ)∈L∗,then

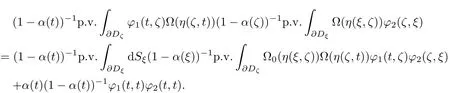
This lemma can be proved similarly to Proposition 1(cf.the proof of Theorem in[4]).

Lemma 3.3(cf.the Proof in Theorem 2.15.3 in[1]) When f(ζ)∈A and f(ζ)never vanishes on∂D,then(f(ζ))−1∈A.

This lemma does not hold in one complex variable,and this shows the essential diff erence between one complex variable and several complex variables.

Theorem 3.4 If a(t)and k0(t,ζ)∈A,b(t)=k0(t,t),when a2(t)−b2(t)and m(t)= a2(t)−(1−2α(t))a(t)b(t)−α(t)(1−α(t))−1b2(t)never vanish on∂D,then(3.1)has a unique solution

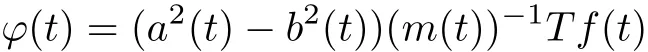
in L∗,the operator T is defined by,forψ∈L∗,

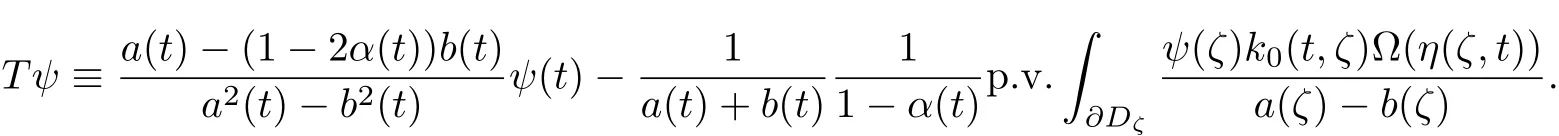
Proof Let T operate(from the left)on the two sides of(3.1).The right side of(3.1)turns into T f and the left side is

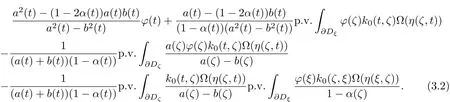
By the assumptions k0(t,ζ)k0(ζ,ξ)(a(ζ)−b(ζ))−1∈L∗.Applying Lemma 3.2,the last term of(3.2)becomes

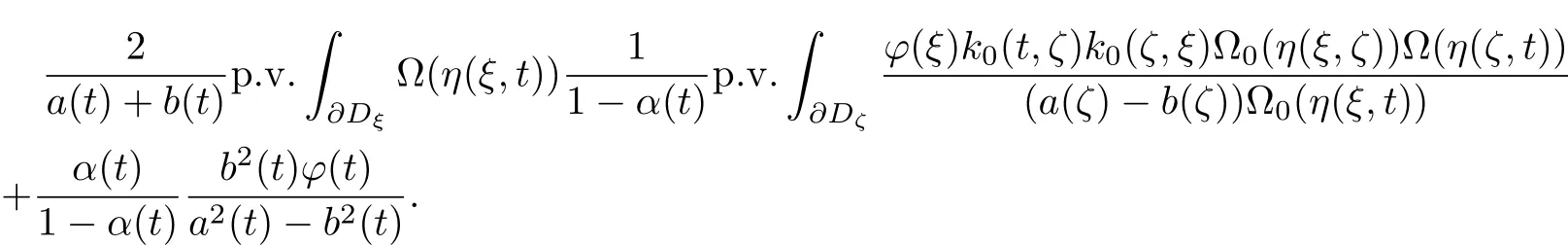
For Lemma 3.3,k0(t,ζ)k0(ζ,ξ)(a(ζ)−b(ζ))−1∈A.By Lemma 3.1,the preceding expression equals

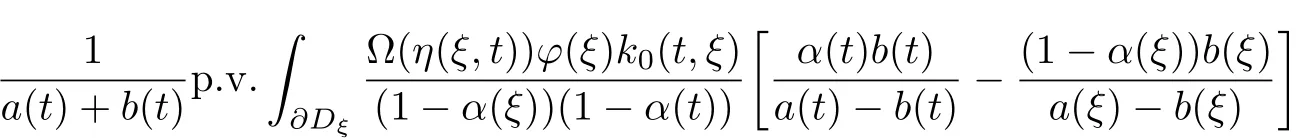
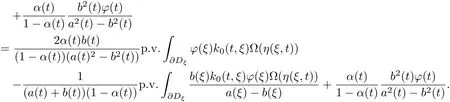
Applying the preceding equation to(3.2),we have

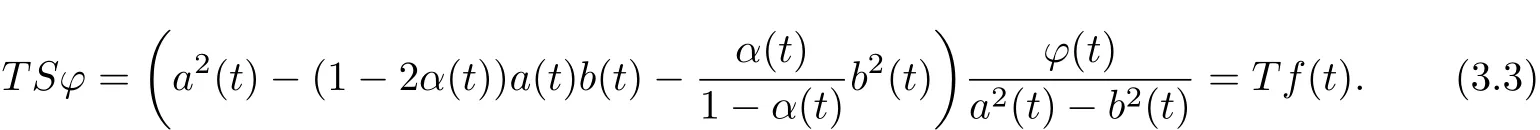
Thenϕ(t)=(a2(t)−b2(t))(m(t))−1T f(t)is a solution of(3.1).Let S defined by(3.1)operate (from the left)on the two sides ofϕ(t)=(a2(t)−b2(t))(m(t))−1T f(t).The same reasoning shows thatϕ(t)=(a2(t)−b2(t))(m(t))−1T f(t)is the unique solution in L∗.Theorem holds.

Theorem 3.4 is the generalization of Proposition 2 and whenthis is the same as Proposition 2(i.e.,Theorem 2.15.3 in[1]).The condition m(t)/=0 in Theorem 3.4 is reasonable,for if m(t)=0,we haveα(t)=0 or 1 and this contradicts the definition ofα(t).

Theorem 3.4 shows that A is an important class of functions.The following Theorem 3.5 can be used to characterize A.

Theorem 3.5 Letϕ(ζ)∈A and define

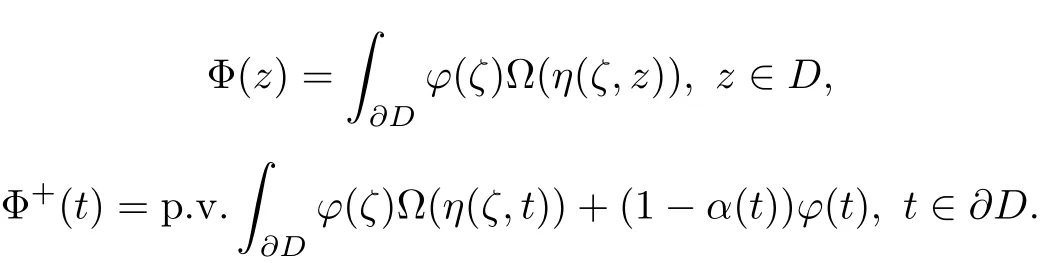
Then we have,when z approaches the boundary point t along any path from the interior of D,we haveMore precisely speaking,ifϕ(ζ)∈Lipα,0＜α≤1,then for any positive numberδless thanαthere exists a positive number K depending only onϕ(ζ)andδ such that when the inner point z of D approaches the boundary,we have the estimate

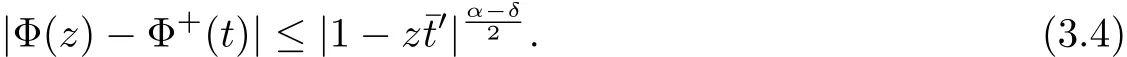
Proof First we prove that,if 0＜ρ＜1 andρ→1,the estimate

holds uniformly forξon∂D.

Without loss of generality,we let a1=(0,0,···,0),t=(1,0,···,0)andρξ∈B1then

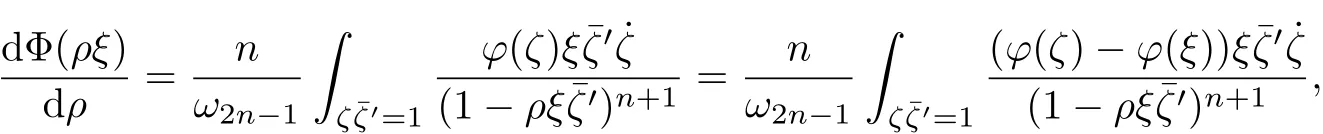
from which it follows that,whenρ→1,

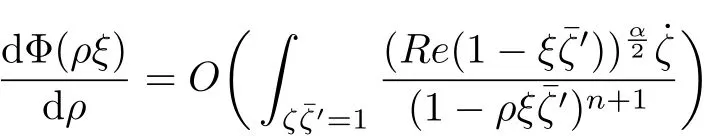
forξon∂D.By Theorem 1.5.2 in[1],Φ+(t)∈Lip(α−δ),whereδis any positive number less thanα.Therefore,there exists a positive number K2depending only onδandϕ(ζ)such that

forξand t on the boundary of D.(3.4)follows whereTheorem holds.

Theorem 3.5 shows that the restriction ofthe path ofthe limit formulas(cf.Plemeljformula in[3])can be eliminated.While the characteristics of A in the building domain of biballs is similar to that on the complex sphere(cf.Theorem 2.15.2 in[1]),so we omit the details.

[1]GONG Sheng.Integral of Cauchy Type on the Ball[M].Boston:International Press,1993.

[2]LIN Liang-yu.Bochner-Martinelli formula with discrete holomorphic kernel[J].Chinese Science Bullitin, 1997,46(6):447-450.

[3]LIN Liang-yu,QIU Chun-hui,RUAN Qi-hua.Boundary behavior for the integrals of Cauchy type on a building domain of complex biballs[J].J Xiamen Univ(Nature Science),1998,37(3):318-332.

[4]GONG Ding-dong,LIN Liang-yu.The Poincar´e-Bertrand formula on the building domina of the complex biballs[J].Acta Mathematica Scientia(Series B),2010,30(1):341-349.

[5]LU Qi-keng,ZHONGTong-de.Extension ofprivalov theorem[J].Acta Mathematics Sinica,1957,7:144-165.

[6]KERZMAN N,STEIN E M.The Szego kernel in terms of Cauchy-Fantappi´e kernels[J].Duck Math J,1978, 45(3):197-224.

[7]WOLFGANG ALT.Singul¨are Integrale mit gemischten Homogenit¨aten auf mannigfaltigkeiten und anwendungen in der funktionentheorie[J].Math Z,1974,137(3):227-256.

[8]ZHONG Tong-de.Transformation formulae of multiple singular integrals with Bochner-Martinelli kernel[J]. Acta Mathematics Sinica,1980,23:554-565.

[9]KYTMANOV A.The Bochner-Martinelli Integral and Its Applications[M].Birkhauser:Verlag,1992.

[10]ZHONG Tong-de,CHEN Lu-ping.The Poincar´e-Bertrand formula for the Bochner-Martinelli integral[J]. Integral Equations Oper Theory(English),2006,54(4):585-595.

[11]LIN Liang-yu,QIU Chun-hui,HUANG Yu-shen.The Plemelj formula of higher order partial derivatives of the Bochner-Martinelli type integral[J].Integral Equations and Operator Theory,2005,53(1)61-73.

[12]GONG Ding-dong,LIN Liang-yu.Several theorems of singular integral on a domain built by complex biballs[J].J Xiamen Univ Nat Sci,2002,41(3):276-279.

tion:32A55,45E05

1002–0462(2014)01–0039–06

Chin.Quart.J.of Math. 2014,29(1):39—44

date:2012-02-20

Supported by the NNSF of China(11171298);Supported by the Natural Science Foundation of Zhejiang Province(Y6110425,Y604563)

Biography:GONG Ding-dong(1968-),male,native of Chuzhou,Anhui,Ph.D.,engages in several complex variables.

CLC number:O174.5 Document code:A