The Lower Order and Type of Solutions of Second Order Diff erential Equation

ZHANG Shao-hua,WU Zhao-jun,SUN Dao-chun

(1.School of Mathematics and Statistics,Hubei University of Science and Technology,Xianning 437100, China;2.School of Mathematics,South China Normal University,Guangzhou 510631,China)

The Lower Order and Type of Solutions of Second Order Diff erential Equation

ZHANG Shao-hua1,WU Zhao-jun1,SUN Dao-chun2

(1.School of Mathematics and Statistics,Hubei University of Science and Technology,Xianning 437100, China;2.School of Mathematics,South China Normal University,Guangzhou 510631,China)

The main purpose of this paper is to study the lower order and type of second order diff erential equation w′′(z)−A(z)w=0,where A(z)is a polynomial.In the case ofthe authors prove that the lower order and the type of all non-trivial solutions w of w′′(z)−A(z)w=0 are equal toandrespectively.In the case of A(z)=adzd+ad−1zd−1+···+a1z+a0,ad＞0,ad−1≥0,···,a1≥0,a0≥0,the authors prove that the lower order of all non-trivial solutions w of w′′(z)−A(z)w=0 is

type;order;lower order;diff erential equation

§1.Introduction and Main Results

Since 1982 when the article by Bank and Laine[1]appeared in Trans Amer Math Soc,there have appeared many papers on the global theory of complex diff erential equations which were studied from the point of view of Nevanlinna theory.We refer the reader to the books by Laine[4]and by Gao et al[2].In[1],Bank and Laine have proved.

Theorem A Suppose that A(z)=adzd+ad−1zd−1+···+a1z+a0,ad/=0 is a polynomial. Then allnon-trivialsolutions f of

have the order of growthσ(f)=

Theorem A study the order of solutions of(1.1).It’s naturalto ask what are the lower order and the type of any one of non-trivial solutions.Upon to now,there isn’t a paper to study this problem.This paper is devoted to consider it.More precisely,we shallprove the following theorems.

Theorem 1 Assume that A(z)=adzd,ad/=0.Then

(i)Allnon-trivialsolutions f of(1.1)have the lower order of growthµ(f)=

(ii)All non-trivial solutions f of(1.1)have the typeTheorem 2 Assume that A(z)=adzd+ad−1zd−1+···+a1z+a0,ad＞0,ad−1≥0,···,a1≥0,a0≥0.Then allnon-trivialsolutions f of(1.1)have the lower order ofgrowth µ(f)=

From Theorem 1,Theorem 2 and Theorem A,we can get

Corollary 1 Assume that A(z)=adzd,ad/=0 or A(z)=adzd+ad−1zd−1+···+a1z+ a0,ad＞0,ad−1≥0,···,a1≥0,a0≥0.Then all non-trivial solutions f of(1.1)are regular growth.

In Theorem 2,we add that condition ad＞0,ad−1≥0,···,a1≥0,a0≥0.Here,we pose the following question.

Question 1 Does Theorem 2 holds if we remove the additional condition of ad＞0,ad−1≥0,···,a1≥0,a0≥0?

§2. The Presentation of Solution of(1.1)

As is well-known,allsolution of(1.1)are entire functions.Let

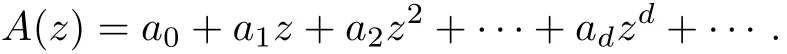
Suppose that

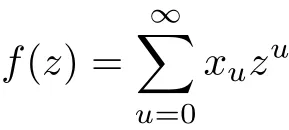
is a non-trivial solution of(1.1).Then

where xv=0 for any v＜0.We can get from(1.1),(2.1)and(2.2)that

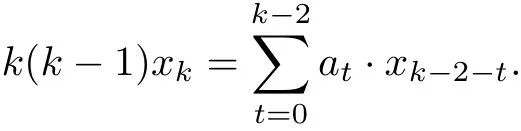
Hence,for any k∈N−{0,1},

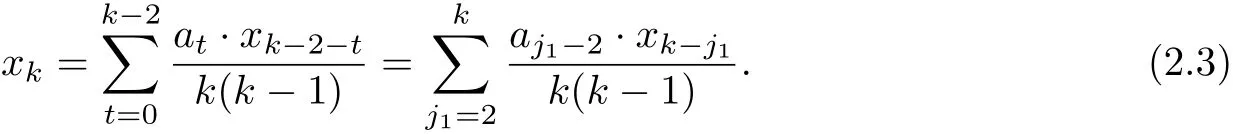
Replace k by k−j1in(2.3),we can get

Subsisting the above equality to(2.3),for any k/=0,1,j1,j1+1,we have

Replace k by k−j1−j2in(2.3),we can get

Subsisting the above equality to(2.3),for any k/=0,1,j1,j1+1,j1+j2,j1+j2+1,we have

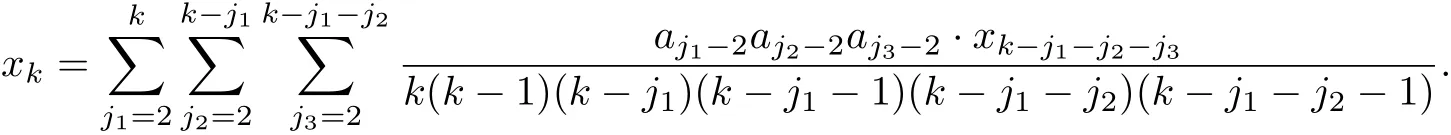
Put x0=c0,x1=c1.By induction,we can get the following coeffi cients formula ofnon-trivial solution of(1.1),

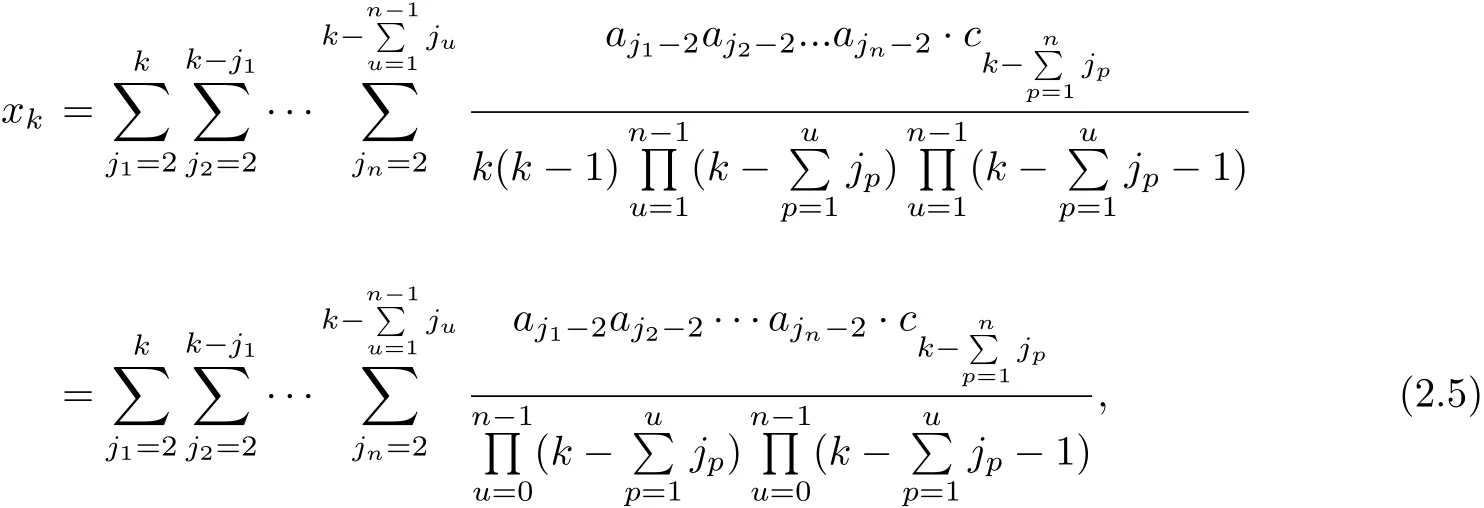
where the Sum for any combination jusuch thatFor any positive integer u,ju≥2.So n≤k/2.Noting that k−0,1,2,···,n−1).Hence,(2.5)is well defined.

Especially,if

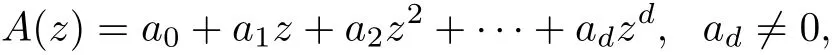
then

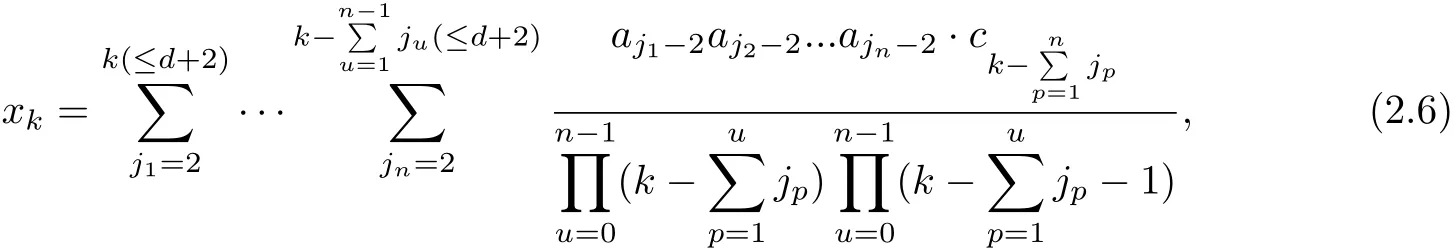
Where the sum for any combination jpsuch that

If A(z)=adzd,ad/=0.Then

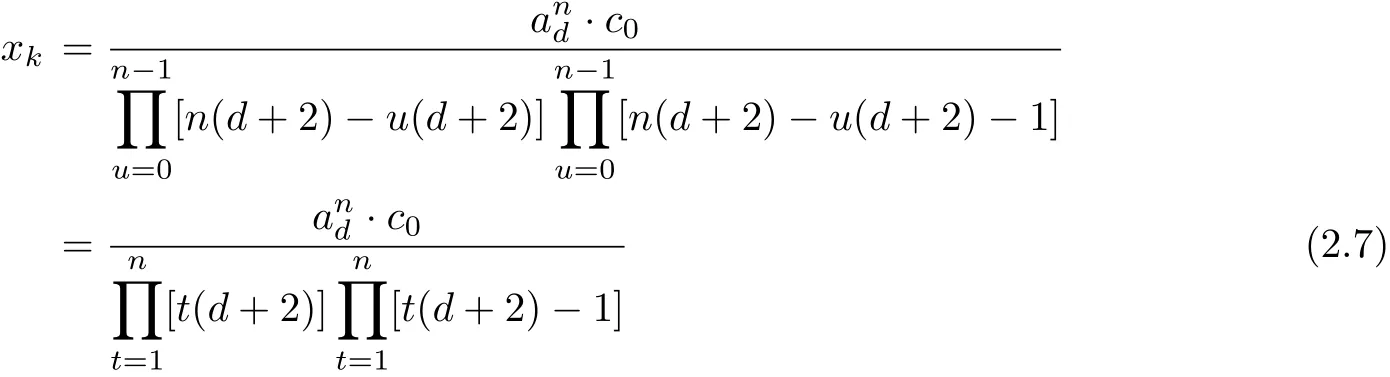
for k=n(d+2);

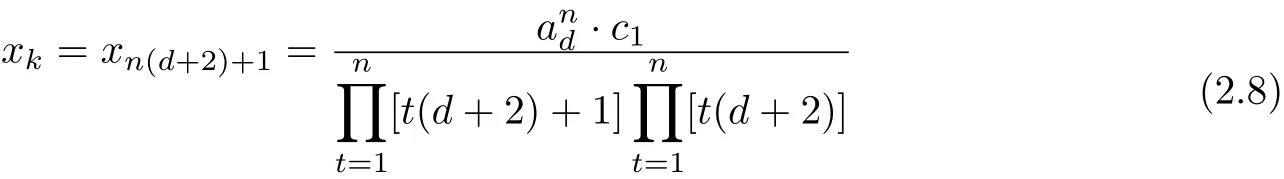
for k=n(d+2)+1 and xk=0 for others.

§3.Proof of Theorems

In order to prove Theorems 1 and 2,we need it following results related to the growth of Taylor series.

Suppose Taylor series

satisfies

Then(3.1)is convergent in the whole complex plane C.We denote it by f(z)and f(z)is an entire function.The maximum module M(r,f),maximum term m(r,f)and central index ν(r,f)of f(z)are defined as the following

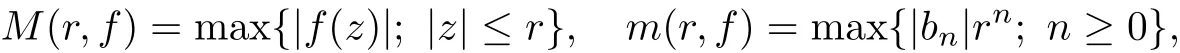
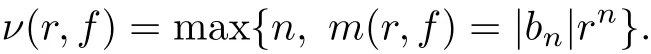
The orderσ(f)and the lower orderµ(f)of f(z)is defined by

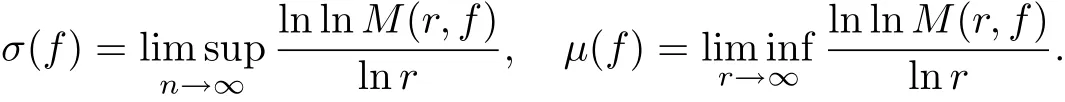
Ifσ(f)=µ(f),then we say f(z)has regular growth orderσ(f).Suppose that the order of f(z) isρ∈(0,∞),we define the type of f(z)by

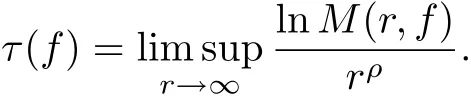
Lemma 1[3,7]Suppose the Taylor series(3.1)satisfies(3.2).Then

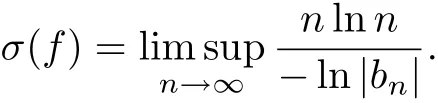
If{nk}is the sequence of centralindex,then

Lemma 2[3,7]Suppose the Taylor series(3.1)satisfies(3.2).Then

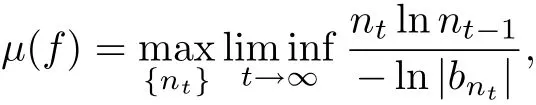
where the Max for any increasing sequence{nt}.

Lemma 3[3,7]Suppose that the order of f(z)isρ∈(0,∞).Then

Theorem 3 Suppose the Taylor series(3.1)satisfies(3.2).Then f(z)has regular growth orderρif and only if the series(3.1)satisfies the following conditions

i)

ii)There is an increasing sequence{nt}such that

Proof Suppose that the series(3.1)satisfies the following conditions

i)

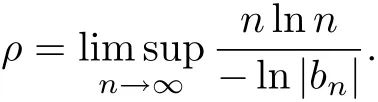
ii)There is an increasing sequence{nt}such that

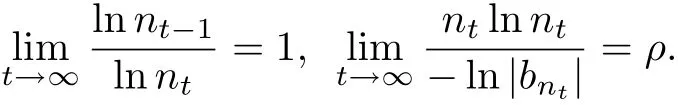
Then

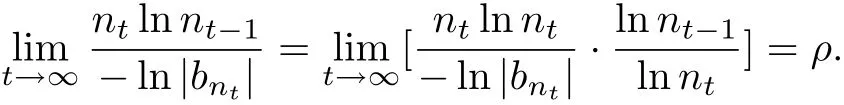
By Lemma 2,we haveµ(f)≥ρ.By Lemma 1,we haveσ(f)≤ρ.So f(z)has regular growth orderρ.

Suppose that f(z)has regular growth orderρ.In virtue Lemmas 1 and 2,we have

i)

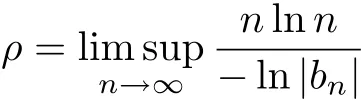
and ii)

for the sequence of central index{nk},whereis a subsequence of{nk}.

We are now in the position to prove theorems 1 and 2.

Proof of Theorem 1 Since

So

Suppose that

is a non-trivial solution of(1.1).By Theorem A and Lemma 1,we have

Take c0/=0 in Section 2.By(2.7)and(3.3),for n=k(d+2),we have

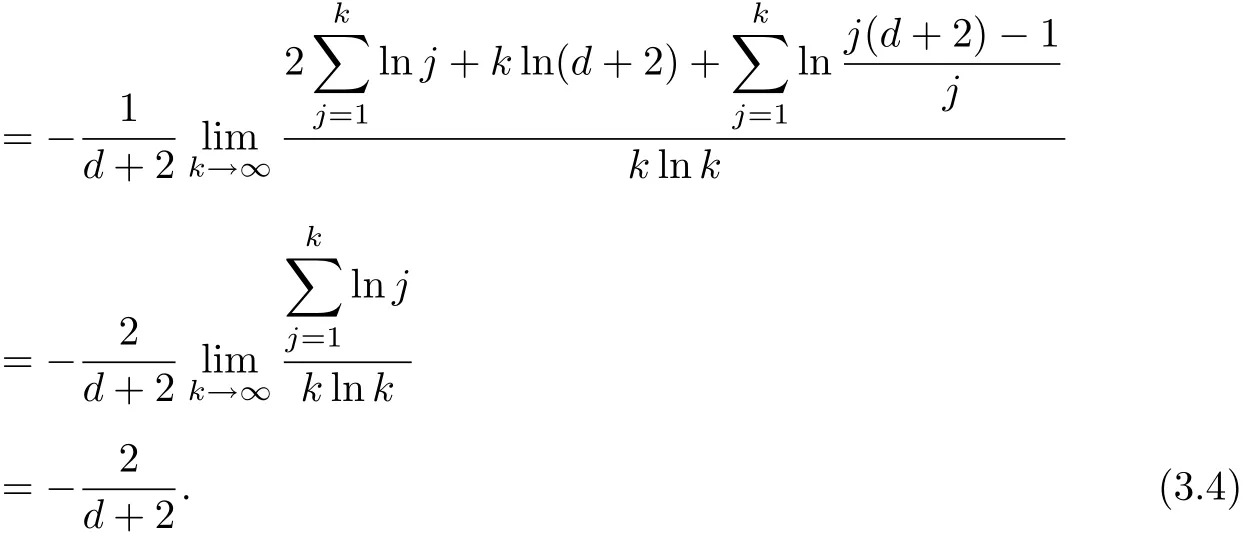
Take c1/=0 in Section 2.By(2.8)and(3.3),for n=k(d+2)+1,we also obtain(3.4).Hence

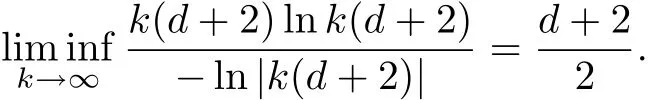
Noting that

By Theorem 3,we derive that f(z)is regular growth and the lower order of f(z)is

Take c0/=0 in Section 2.By Lemma 3,(2.7)and(3.3),for n=k(d+2),we have

Take c1/=0 in Section 2.By(2.8)and(3.3),for n=k(d+2)+1,we also obtain(3.5).

Proof of Theorem 2 Take c1/=0 in Section 2.By Lemma 3,(2.6)and(3.3),for n(t):=t(d+2)+1,we have

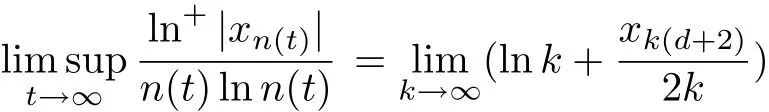
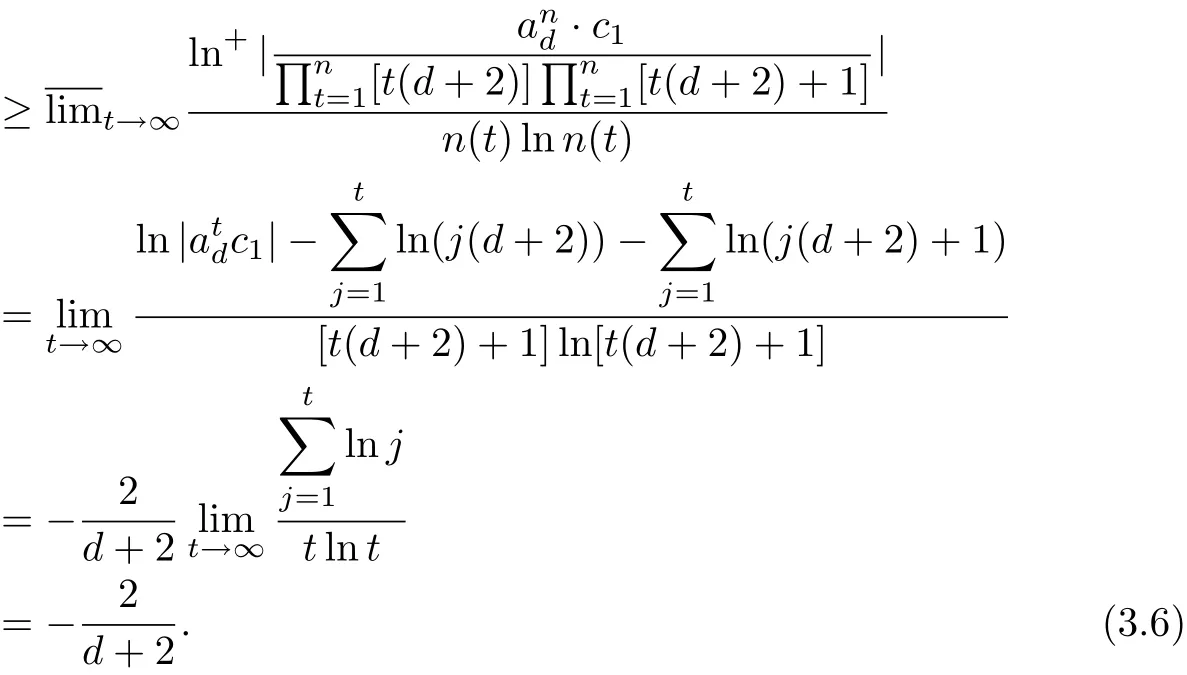
If c1=0,then c0/=0 in Section 2.By(2.8)and(3.3),for n=k(d+2),we also obtain (3.6).By Theorem 3,we derive that f(z)is regular growth and the lower order of f(z)is

[1]BANK STEVEN B,LAINE ILPO.On the oscillation theory of f′+Af=0 where A is entire[J].Trans Amer Math Soc,1982,273(1):351-363.

[2]GAO Shi-an,CHEN Zong-xuan,CHEN Te-wei.Oscillation Theory of Linear Diff erential Equation[M]. Wuhan:Huazhong University of Science and Technology Press,1998.

[3]HE Yu-zhan,XIAO Xiu-zhi.Algebroid Function and Ordinary Differential Equation[M].Beijing:Science Press,1988.

[4]LAINE ILPO.Nevanlinna Theory and Complex Diff erential Equations[M].Berlin:Walter de Gruyter Co, 1993.

[5]SHEREMETA Z M.On entire solutions of a diff erential equation[J].Matematychni Studii,2000,14(1): 54C58.

[6]CHEN Yu-xian,WU Zhao-jun.On the location of zeros of higher order diff erential equation[J].Chin Quart J of Math,2010,25(1):92-97.

[7]YU Jia-rong.Dirichlet Series and Random Dirichlet Series[M].Beijing:Science Press,1994.

tion:30D30

1002–0462(2014)01–0014–08

Chin.Quart.J.of Math. 2014,29(1):14—21

date:2013-04-08

Supported by the NNSF of China(11201395);Supported by the Science Foundation of Educational Commission of Hubei Province(Q20132801)

Biographies:ZHANG Shao-hua(1961-),male,native of Xianning,Hubei,an associate professor of Hubei University of Science and Technology,engages in complex analysis;WU Zhao-jun(1978-),male,native of Xianning,Hubei,an associate professor of Hubei University of Science and Technology,Ph.D.,engages in complex analysis.

CLC number:O174.32 Document code:A