Composition Operators on the Weighted Bergman Space in the Unit Polydisk

HU Rong,HU Peng-yan

(1.College of Mathematics and Finance-Economics,Sichuan University of Arts and Science,Dazhou 635000,China;2.College of Mathematics and Computational Science,Shenzhen University,Shenzhen 518060,China)

Composition Operators on the Weighted Bergman Space in the Unit Polydisk

HU Rong1,HU Peng-yan2

(1.College of Mathematics and Finance-Economics,Sichuan University of Arts and Science,Dazhou 635000,China;2.College of Mathematics and Computational Science,Shenzhen University,Shenzhen 518060,China)

We consider the boundedness of composition operators on the Bergman space, and shows that when it is induced by automorphism is always bounded.At first we got a change of variables formula,which is very important for the proof of the boundedness of composition operators,and then obtain an upper bound for the special operator norm on Bergman space.

bergman space;polydisk;composition operators;automorphism

§1. Introduction

Let U be the unit disk in the complex plane and dA be the normalized area measure on U. Forα＞−1,z∈U,let

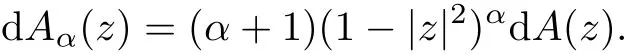
More generally,let Unbe the unit polydisk inℂnand forα＞−1,z=(z1,z2,···,zn)∈Un,

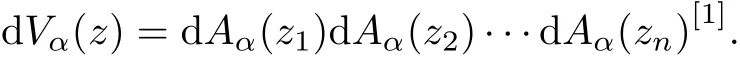
Let a=(a1,a2,···,an)∈Unandϕabe the involution of Un,thenϕa(0)=a and

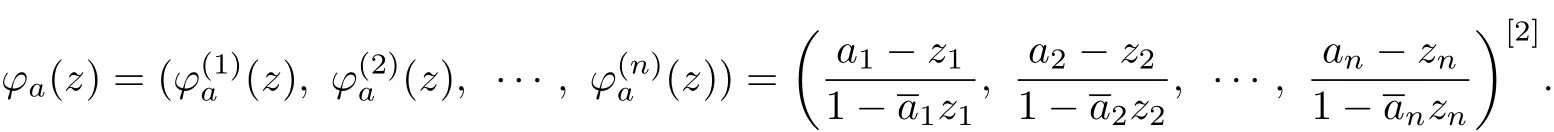
Defi nition 1[2]Supposeα＞−1 and p＞0.f defined on Unis said to be in Lp(Un,d Vα) if

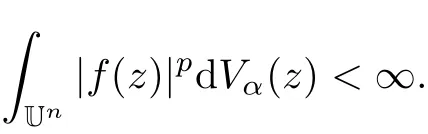
Defi nition 2[2]Let H(Un)be the class ofallholomorphic functions with domain Un.For α＞−1 and p＞0 the weighted Bergman spaceis defined as

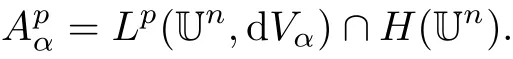
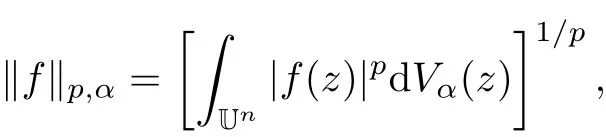
which is called the Bergman norm of f in

Letϕbe a holomorphic map of Un.For f∈H(Un),the composition operators Cϕis defined by Cϕ(f)=f◦ϕ.The boundedness of Cϕon functions space have been studied by many mathematicians,see[3-9].For example,it is proved that Cϕis bounded on the Bergman space in unit disk and the Bloch space in unit polydisk.When n=1,it is well-known that Cϕis bounded on each of spaceand

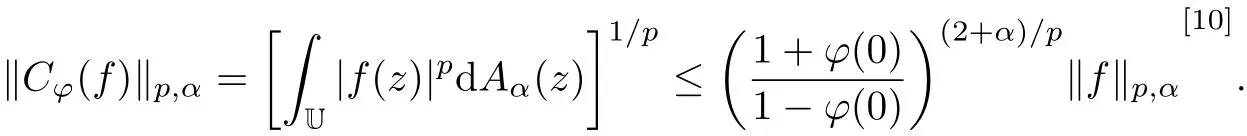
But this result does not extend to the higher dimensional polydisk.For example,the map ϕ(z1,z2,···,zn)=(z1,z2,···,zn)is known to induce an unbounded composition operator onsee[11].

In this paper we obtain that the composition operator Cϕinduced by the automorphism of Unis bounded on the Bergman spaceand also get an upper bound of this kind of the operator.Before proving the main result,we give a change of variables formula which is very important for us.

§2.Main Results

On the unit ball Bnofℂn,we have

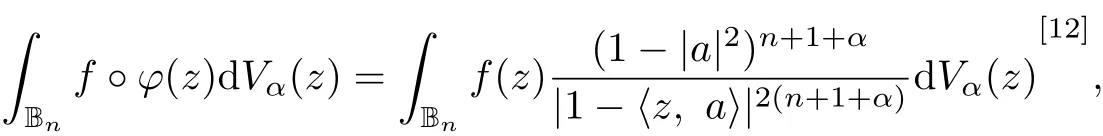
whereϕis a automorphism of Bn,f∈L1(Bn,d Vα)and a=ϕ(0).

In this paper,as the first main result,we obtain a similar formula on the unit polydisk which have great help for the second.

Theorem 1 Let Aut(Un)denote the class of all automorphism with domain Un.Suppose f∈L1(Un,d Vα),there existsθ1,θ2,···,θnand permutationτ:(1,2,···,n)→(1,2,···,n),such that

whereϕ∈Aut(Un)and a=(a1,a2,···,an)=ϕ(0).

The boundedness of composition operator Cϕwhich induced by the automorphism of Unis the following.

Theorem 2 Let 0＜p＜∞andα＞−1.For anyϕ∈Aut(Un),the composition operator Cϕis bounded onand the operator norm satisfies

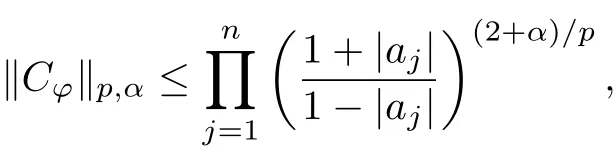
where a=(a1,a2,···,an)=ϕ(0).

In order to prove the main results,we need the following lemmas.

Lemma 1[13]Let JRϕadenote the real Jacobian determinant of involutionϕaof Un,then

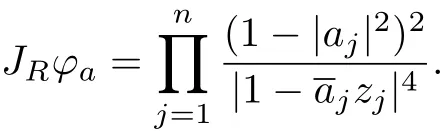
Lemma 2[14]For anyϕ∈Aut(Un),there exists a linear mapping F(z)=(eiθ1zτ(1),···, eiθnzτ(n))and a point a∈Un,such that

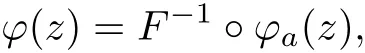
whereϕais a involution of Un,θ1,θ2,···,θnare real numbers andτ:(1,2,···,n)→(1,2,···,n)is a permutation.

We are now in a position to prove the main results.

Proof of Theorem 1 We discuss this in two different conditions.

(a)If a=0,by the proof of Lemma 2,there exists a permutationτ:(1,2,···,n)→(1,2,···,n)such that

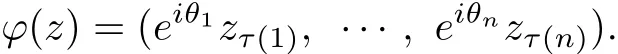
It is wellknown that

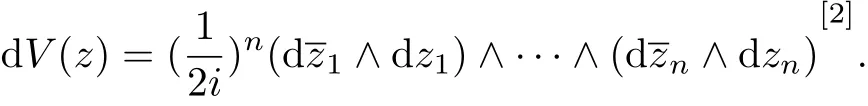
So itcould be proved that d V(z)is invariant under the action ofϕ(z)=(eiθ1zτ(1),···,eiθnzτ(n)). Since

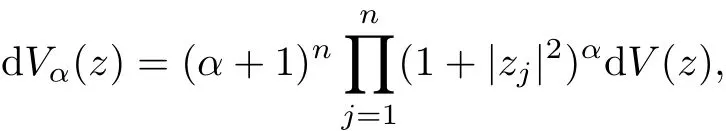
then by a natural change of variables z=ϕ−1(w)and taking notice thatϕ−1andϕhave the same structure,we have d V(ϕ−1(w))=d V(w).The desired result could be produced.

(b)If a/=0,by Lemma 2,there exists a linear mapping F(z)=(eiθ1zτ(1),···,eiθnzτ(n)) such that

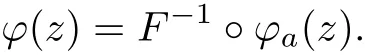
Let z=ϕa◦F(w)=ϕ−1a◦F(w),then

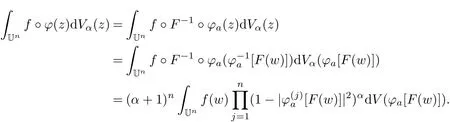
Since

where JRϕa[F(w)]is the real Jacobian determinant ofϕaat point F(w),then by Lemma 1,we have

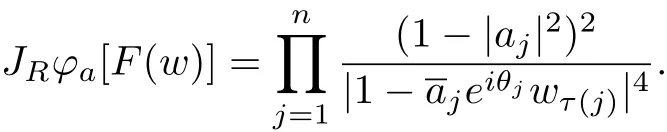
Also we can easily obtain that

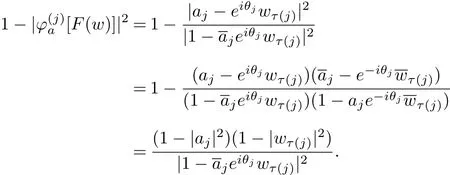
So we have

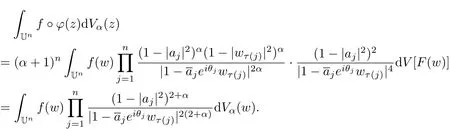
Proof of Theorem 2 For f∈Apα(Un),by Definition 2 and Theorem 1 we have

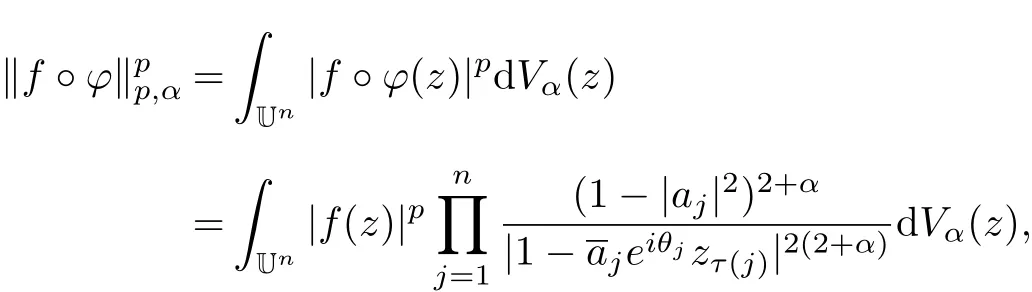
where

Then

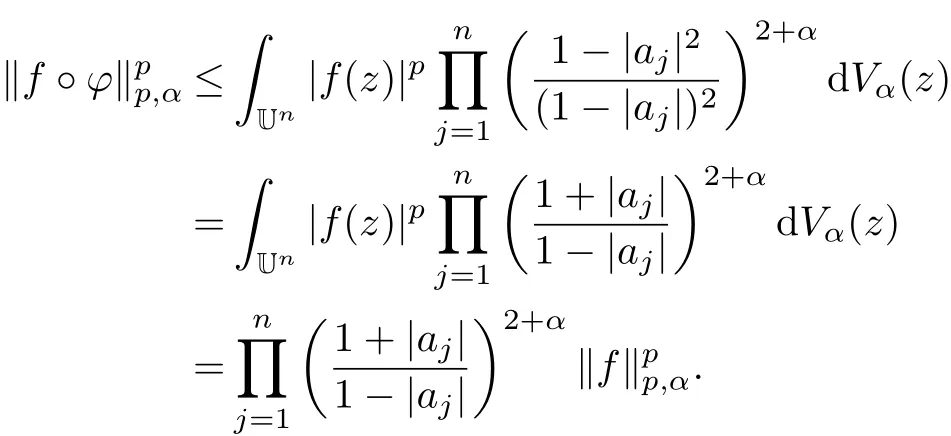
This shows that the composition operators Cϕ(f)=f◦ϕis bounded on Apα(Un)and the desired result is proved.

[1]KOO HYUNGWOON,MICHAEL STESSIN,ZHU Ke-he.Composition operators on the polydisc induced by smooth symbols[J].Journal of Functional Analysis,2008,254:2911-2925.

[2]STEVEN G,KRANTZ.Function Theory of Several Complex Variables[M].Rhode Island:AMS Chelsea Publishing,2000:1-58.

[3]XU Hui-ming,LIU Tai-shun.Weighted composition operators between hardy space on the unit ball[J]. Chinese Quarterly Journal of Mathematics,2004,19(2):111-119.

[4]HU Xiao-jiao,ZHANG Guo-feng,YU Tao.Weighted composition operators on Bergman space and applications[J].Journal of Mathematics,2012,32(1):1-8.

[5]HU Rong.The upper bound of a special class of composition operators on the Bloch space[J].Sichuan University of Arts and Science Journal,2013,23(2):17-19.

[6]GUO Ji-dong,LIU Pin,GAO Wen-hua.Boundedness of weighted composition operators on Bloch type spaces[J].Chinese Quarterly Journal of Mathematics,2008,23(3):356-359.

[7]STEVO STEVI.Composition operators from the weighted Bergman space to the weighted spaces on the unit disc[J].Discrete Dynamics in Nature and Society,2009,10:1-12.

[8]ZHOU Ze-hua,WEI Zhong-qi.Weighted composition operator on the Bloch space in polydiscs[J].Journal of Mathematics,2005,25(4):435-440.

[9]LU Yu-feng.Compact operators on the Bergman spaces of the unit ball and the polydisk in[J].Northeast Math J,2000,16(3):347-356.

[10]TO Pei-jia,PETER.Operator Theory in Function Spaces[M].New York and Basel:Marcel Deken,Inc, 1990:211-220.

[11]STESSIN M,ZHU Ke-he.Composition operators induced by symbols defi ned on a polydisc[J].J Math Anal Appl,2006,319:815-829.

[12]ZHU Ke-he.Spaces of Holomorphic Functions in the Unit Ball[M].New York:Springer-Verlag,2004:5-26.

[13]HU Rong.The weighted Bergman space on the polydisk and the upper boundary of Bergman function[J]. Journal of China West Normal University,2012,33(4):36-39.

[14]SHI Ji-huai.Several Complex Variable Function Theory[M].Beijing:Higher Education Press,1996:55-70.

tion:32A30,47B38

1002–0462(2014)01–0009–05

Chin.Quart.J.of Math. 2014,29(1):9—13

date:2013-10-17

Supported by the Scientific Research Fund of Sichuan Provincial Education Department(13ZB0101)

Biography:HU Rong(1985-),female,native of Nanchong,Sichuan,a lecturer of Sichuan University of Arts and Science,M.S.D.,engages in several complex.

CLC number:O174.56 Document code:A