剃齿刀修形砂轮斜截面法数控精密加工机理研究

陈 彬，吴玉国，吴 胜，时礼平

(安徽工业大学机械工程学院，安徽马鞍山 243032)

剃齿刀修形砂轮斜截面法数控精密加工机理研究

陈 彬，吴玉国，吴 胜，时礼平

(安徽工业大学机械工程学院，安徽马鞍山 243032)

剃齿刀修形砂轮侧面突起是弦长弦高比很大的圆弧，现有数控插补算法无法加工出符合精度要求的修形砂轮。针对这一缺陷，提出斜截面法放大弦高从而减小弦长弦高比的方法，推导加工曲线的方程，并结合算例，获得离散点坐标和加工刀具轨迹。结果表明通过斜截面法放大弦高的加工方式可以获得较高精度的插补轨迹。同时也为大曲率小圆弧曲面的数控加工奠定了一定的理论基础。

剃齿；修形砂轮；斜截面法；数控加工

剃齿是齿轮精加工的高效传统工艺，在齿轮生产中得到广泛应用。剃齿加工过程中，被剃齿轮齿廓的中部多形成中凹，中凹量在0.01～0.03mm范围，这种中凹的齿廓降低了齿轮的啮合性能和传动精度，引起噪声，影响齿轮的承载能力和使用寿命[1-2]。现有的解决方法主要是采用负变位剃齿刀剃齿、随机修形以及剃齿刀补偿修形。负变位剃齿刀剃齿的核心问题是找到能够减小齿廓中凹现象的节圆法向啮合角[3-4]；随机修形是将一个与被剃齿轮几何参数一致的超硬修磨轮取代被剃齿轮与剃齿刀啮合，致使剃齿刀齿廓被修形，再使用修形后的剃齿刀进行剃削加工，消除中凹现象[5-6]；剃齿刀补偿修形是将剃齿刀在齿形节圆附近使用修形砂轮修成中凹进行补偿[7-8]。采用数控方法加工修形砂轮时，修形砂轮侧面突起是弦长弦高比很大的圆弧，弦高对应齿廓中部的中凹量(0.01～0.03mm)，而常用数控系统的位移最小增量为0.001～0.010mm/脉冲，只能将修形砂轮侧面突起圆弧段近似用直线取代，很难实现数控精密加工。因此，寻求高效、高精度的剃齿刀修形砂轮数控加工方法对剃齿工艺有重要意义。为此，文中提出1种通过斜截面放大弦高从而减小弦长弦高比的新方法进行剃齿刀修形砂轮数控精密加工，推导加工曲线方程，且进行算例分析。

1 斜截面法数控精密加工原理

剃齿刀修形砂轮截面形状如图1所示。砂轮侧面突起的圆弧部分用于剃齿刀的修形，将剃齿刀修成中凹形状，作为补偿量。如图2所示，其弦高H表示中凹量，仅为0.01～0.03mm，普通数控机床加工这条圆弧难度很大。图3是针对剃齿刀修形砂轮的斜截面法数控精密加工的原理图。过ox轴作与xoy平面成θ角的xoy′平面，与圆弧环形成放大曲线。放大曲线的顶点到ox轴的距离与θ角有关，当θ角较大时，放大曲线的顶点到ox线距离远大于原有圆弧的弦高(即中凹量)。若以放大曲线取代原有圆弧进行砂轮数控加工，相当于将圆弧进行了放大，放大倍数与θ角有关。由此，斜截面法可以提高砂轮加工精度，进而使剃齿刀的中凹补偿更加精确。

图1 剃齿刀修形砂轮截面形状Fig.1 Section shape of the dressing wheel of the shaving cutter

图2 突起圆弧放大图Fig.2 Enlargementof protruding arc

图3 斜截面法数控精密加工原理示意图Fig.3 Schematic diagram of theoblique section m ethod of CNC precisionmachining

2 放大曲线方程的推导

砂轮侧面突起部分相当于圆弧绕y轴旋转1周得到的，再用一通过ox且与xoy平面成θ角的平面切于突起部分得到放大曲线，放大曲线即为斜截面法的加工曲线。

2.1 圆弧环方程

圆弧所在的坐标系如图4所示，图中：S为圆弧内侧距砂轮中心o的长度；L为圆弧的弧长；H为圆弧的弦高；R为圆弧的半径；o1(x1，y1) 为圆弧的圆心位置。根据圆弧的相关性质得解

其中

图4 圆弧所在坐标系Fig.4 Coordinate system of the circular arc

圆弧绕y轴旋转1周得到圆弧环，圆弧环方程

2.2 放大曲线方程

平面xoy′与xoy平面成θ角，则其平面方程为

联立式(3)，(4)得到放大曲线的方程

其中1/cosθ即为弦高的放大倍数。

3 算例

剃齿刀修形砂轮的突起位置距砂轮轴线S=50mm，突起圆弧部分的弦高为H=0.01mm，弦长为L=0.08mm。若取放大倍数为5倍，即

3.1 理论计算

将上述数据带入式(5)得，并使用MATLAB进行曲线绘制[9]，绘制出的曲线如图5所示。选取x≥0，y≥0的部分进行分析。

利用MATLAB求出原有圆弧在笛卡尔坐标系中的坐标和放大曲线在斜截面中的坐标，将坐标值(根据精度要求)进行对比，x轴步长取0.01mm。如表1。

从表1中的数据可知当x=50.04时，放大曲线的弦高为原有圆弧弦高的5倍，与算例中所取的放大倍数一致。

3.2 插补对比

利用斜截面法进行加工时，走刀由oxy平面变成oxy'平面。将表1中的离散坐标值利用数控插补功能转化为数控加工的走刀轨迹[10]，若取数控系统的位移最小命令增量0.01mm/脉冲，使用逐点比较插补的方法得到如图6所示的轨迹，图6(a)是使用普通加工方得到的轨迹，图6(b)是使用斜截面法加工得到的轨迹。比较2种轨迹，可以看出普通方法不能加工出此砂轮侧面突起圆弧，而使用斜截面法进行加工可以得到质量较高的曲线，进而可提高砂轮的加工精度。

图5 MATLAB绘制的曲线Fig.5 Curve drawn by M ATLAB

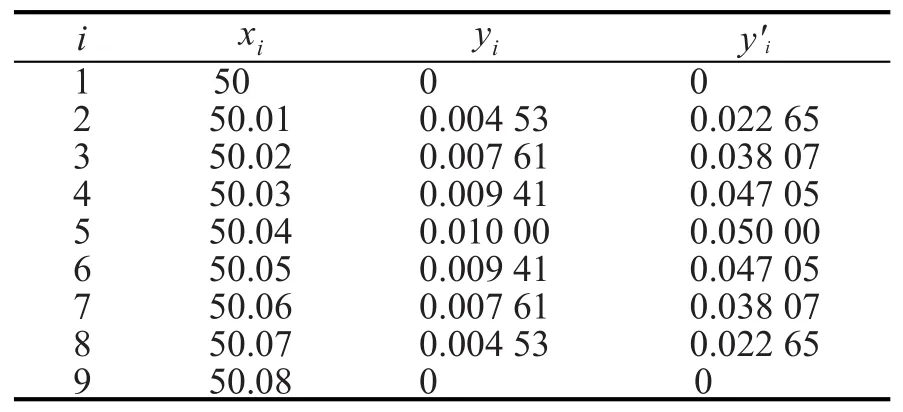
表1 曲线中各点坐标(单位：mm)Tab.1 Coordinatesof each point in the curve(Unit:mm)

图6 走刀轨迹Fig.6 Cutting path

4 结 论

提出了1种通过斜截面法放大弦高进行剃齿刀修形砂轮数控精密加工的新方法，推导了加工曲线方程，并结合算例进行分析。结果表明该方法加工出的剃齿刀修形砂轮质量较好，间接提高了剃齿刀补偿的精度，从而使剃齿精度得到了改善。同时也为大曲率小圆弧曲面的数控加工奠定了一定的理论基础。

[1]蔡安江,郭师虹,董朝阳,等.剃齿刀精确修形技术[J].沈阳工业大学学报,2010,32(3):296-299.

[2]Golovko A N.Kinematic calculation of the error in gearshaving[J].Russian Engineering Research,2011,31(10):1034-1035.

[3]陈世平,廖林清,石军.剃齿加工齿形中凹误差分析[J].现代制造工程,2002(10):52-53.

[4]蔡安江,张振军,阮晓光.基于剃齿修形的啮合角数值计算[J].中国机械工程,2013,32(10):1327-1330.

[5]胡敏.剃齿刀修形技术及其CAD系统的研究[D].西安：西安建筑科技大学,2009:7-9.

[6]詹东安,任济生,王素玉,等.随机修形剃齿刀消除剃齿齿形中凹的机理研究[J].西安交通大学学报，1999,33(8):44-47.

[7]彭娟媚,王光华.提高齿轮滚剃齿精度及解决齿形中凹问题研究[J].制造技术与机床,2008(3):87-91.

[8]殷崇一,刘义,杨选文.剃刀的一种对应点修形新方法和实践[J].机械传动,2011,35(7):79-81.

[9]陈怀琛.MATLAB及其在理工课程中的应用指南[M].西安：西安电子科技大学出版社,2007:31-40.

[10]李斌,李曦.数控技术[M].武汉：湖北科学技术出版社,2010:107-110.

责任编辑：何莉

A Study of theMechanism of CNC Precision Machining of Oblique Section Method to the DressWheelof the Shaving Cutter

CHEN Bin,WU Yuguo,WU Sheng,SHILiping
(SchoolofMechanicalEngineering,AnhuiUniversity of Technology,Ma'anshan 243032,China)

The protrusion of the dressing wheelof the shaving cutter is an arc which the ratio of chord length and chord height is too large.CNC interpolation algorithm atpresent is difficult to process thewheelwhich ismet the accuracy requirements.According to the defect,a new machining method through oblique section to enlarge chord heightand derive the equations of the theoretical curvewas proposed.Combined w ith example,coordinate point andmachining path were obtained.The results show that themachiningmethod through oblique section to enlarge chord height can acquire precision of interpolation trajectory,and it provides theoretical basis for CNC machining of large curvature small circulararc curved surface.

gear shaving;wheel;oblique section;CNCmachining

TH161.12

A

10.3969/j.issn.1671-7872.2014.01.015

1671-7872(2014)01-0068-03

2013-10-12

安徽省高校省级自然科学研究重点项目(kJ2010A054)

陈彬(1990-)，男，安徽宿松人，硕士生，研究方向为机电液一体化技术、先进制造技术。

吴玉国(1961-)，男，安徽安庆人，教授，研究方向为数控技术理论与应用、先进制造技术开发应用。