一道高考数列试题解法的探究

刘铁龙

（延边第二中学，吉林 延吉 133000）

2012年新课标高考数学（理科）试卷中出现了一道数列填空题，此题看似很简单，却让考生无从下手，找不到解题的规律。为此笔者进行了研究，得到几种不同的解法，供大家探讨。

题目：已知数列﹛an﹜满足an+1+(-1)nan=2n-1，求数列﹛an﹜的前60项和（基于教学分析的需要，保留了标准答案中的两种解法）。

方法一：可证明：bn+1=a4n+1+a4n+2+a4n+3+a4n+4=a4n-3+a4n-2+a4n-2+a4n+16=bn+16

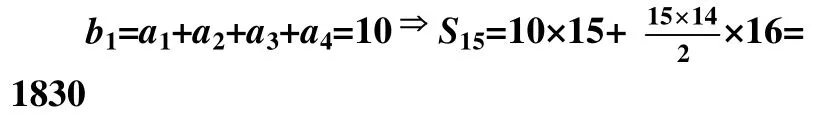
方法二：an+2=(-1)nan+1+2n+1=(-1)n[(-)n-1an+2 n-1]+2n+1

设K为非负整数，则

以上两种解法非常巧妙，体现了数列知识的 规律性，但对于学生来说不易理解。根据学生的认知规律，我利用由一般到特殊的规律，探讨了以下三种解法：

由已知得

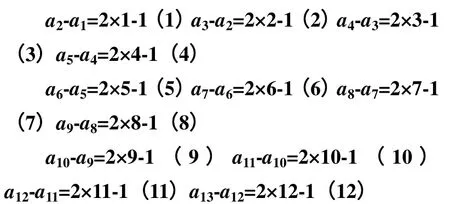
方法一：

由(2)—(1) 得a3+a1=2 ，由（2）+（3）得a2+a4=8， 所以a1+a2+a3+a4=1+2+3+4=10

由（6）—（5）得a5+a7=2 ，由（7）+（6）得a8+a6=24 ， 所以 a5+a6+a7+a8=5+6+7+8=26

(10)—得a9+a11=2 ，(11)+(11)a10+a12=40，所以a9+a10+a11+a12=9+10+11+12=42

a57+a58+a59+a60=57+58+59+60=234

由以上规律可知数列﹛an﹜满足：S4，S8-S4,S12-S8......S60-S56是以10为首项，16为公差的等差数列，因此S60=1830

[评析]：此题是求一个数列﹛an﹜的前60项的和，但这个数列不具备等差数列和等比数列的性质，因此不能用求和公式来求。因此我们需要研究此数列具备的其他规律，通过计算发现数列﹛an﹜满足：S4，S8-S4,S12-S8......S60-S56是以10为首项，16为公差的等差数列，从而得到解决。这种方法简单易懂，符合学生的认知规律，紧扣课本对数列知识的要求。因此教师在课堂教学时要以教材为中心，紧扣教材使学生不仅学到解决问题本身的解决方法，可能还会学到怎样学习的一些方法，使学生更能主动的学生数学。

方法二：

由（2）—（1）得 a3+a1=2，由（4）—（3）得a3+a5=2，（6）—（5）得a5+a7=2.............

由以上规律：a2n-1+a2n+1=2

因此有：a1=a5=a9=a13......=a57=a61和a3=a7.=a11=a15=......=a59

由方法一：知a2+a4=8 a8+a6=24 a10+a12=40...............a2（2n-1）+a4n=8(2n-1)

即数列﹛a2(2n-1)a4n﹜是以8为首项，16为公差的等差数列，结合a2n-1+a2n+1=2可知数列 ﹛an﹜满足, s8_ s4, s12_ s8. .. .. .. . .s60_ s56是以10为首项，16为公差的等差数列，因此S60=1830

[评析]：通过数列知识的学习，我们知道若﹛an﹜和﹛bn﹜都是等差数列，则数列﹛an+bn﹜也是等差数列，针对这个结论，我们探讨如何利用这个知识解决这道题。通过研究会发现数列﹛a2（2n-1）+a4n﹜是以8为首项，16为公差的等差数列，结合a2n-1+a2n+1=2可知数列﹛an﹜满足：S4，S8-S4,S12-S8......S60-S56是以10为首项，16为公差的等差数列，从而使问题得以解决。对一些表面上没有规律而言的问题，要注意寻找研究问题的突破口，从中发现一些有价值的线索，从特殊中发现规律。促进问题的认识。

方法三：

由方法二知a1=a5=a9=a13......=a57=a61。即有a1=a61。因此将上式累加得：

[评析]：此题是涉及相邻两项之间用连接的求和问题，因此涉及到了n为奇偶问题，当n为偶数时，会发现从第二项起数列﹛a2n+a2n+1﹜构成等差数列，由此得到和：(a2+a3)+ (a4+a5)+(a6+a7)+(a8+a9)+......+(a60+a61)，由此可以利用等价转换思想探讨a1和a61是否相等。通过此解法，可以使问题解法指向明确，解答过程有章可循。

在教学中，注意挖掘所学知识的内在规律，进行灵活变化，对一些表面上没有规律而言的问题，从中发现一些有价值的线索，从特殊中发现规律，促进问题的认识。