基于振动的简支梁裂纹损伤识别研究*

(陆军军官学院 合肥 230031)

基于振动的简支梁裂纹损伤识别研究*

邹志强吴斌

(陆军军官学院 合肥 230031)

针对传统损伤检测对早期裂纹不敏感的问题,研究了基于振动的裂纹损伤检测。文中对简支梁的裂纹损伤进行了理论分析、数值模拟和实验研究,结果表明简支梁的各阶模态频率随着裂纹深度的的增加而减小,证实了基于模态频率检测裂纹损伤的可行性,为损伤的早期检测提供了依据。

振动; 简支梁; 损伤检测; 模态频率

ClassNumberTP39

1 引言

大型工程结构的灾难性事故常常因为微小裂缝而引起,所以利用非破坏方法检测结构的损伤成为国内外研究人员关注的热点课题。结构的振动诊断同超声波探伤、X射线照相术、声波探测等无损检验技术相比,振动具有信号提取方便可靠,传感器可以安装在人们不宜接近的结构部位等优点,所以结构振动模态分析技术已经成为结构无损检测技术的重要方法。王璋奇[1]等以悬臂梁振动理论作为基础,利用裂纹悬臂梁振动模态频率的特征能够提出一种辨识裂纹深度和位置参数的数值计算方法。Stubbs[2]和Comwell[3]分别提出基于应变能变化的一维梁的损伤监测,并将应变能这一理论扩展到对板结构的损伤检测中。朱宏平[4]等评述了国内外损伤检测方法的优缺点,提出基于动力检测前期裂纹的可行性。但由于影响结构模态参数的因素较多,目前尚无统一和有效的对结构损伤程度和位置敏感的特征参数,加上大型复杂结构振动模态识别技术发展的限制,用振动诊断对结构进行损伤检测的研究大多使用诸如简支梁这样的简单结构进行验证。

裂纹的检测和识别对于保证构件的正常使用,预防突发灾难性后果具有重要意义。裂纹的产生和扩展对构件振动特性必然产生一定的影响,固有频率和振型等结构动力参数将发生相应的变化。本文基于振动分析,对含裂纹简支梁的损伤进行了理论分析、数值模拟和实验验证。结果表明,简支梁的各阶模态频率随着裂纹深度的的增加而减小,且裂纹对模态频率的影响随着裂纹深度的增大而增大。

2 理论分析

简支梁经离散化处理后,动态特性由N阶矩阵微分方程描述[5]:

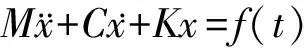
(1)

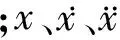
设系统的初始状态为零,对式(1)两边进行拉普拉斯变换,可以得到以复数s为变量的矩阵代数方程:

[Ms2+Cs+K]X(s)=F(s)

(2)

H(ω)中第i行第j列的元素等于仅在j坐标激振时,i坐标响应与激振力之比,即:

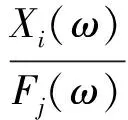
(3)

因此

(4)

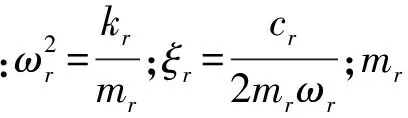
图1 含裂纹的简支梁示意图

结构模态参数(频率、振型等)是结构物理特性(质量、阻尼和刚度等)的函数,因而结构的物理特性的改变必然会引起结构动力响应的改变。以图1中的简支梁为例,确定简支梁物理参数为:材料弹性模量E=206GPa,泊松比μ=0.3,密度ρ=7850kg/m3,梁的几何参数:长度L=0.635m,宽度B=0.015m,高度H=0.01m,裂纹宽0.002m,裂纹距离左端为a,裂纹深度为b。将一些参量进行无量纲化处理:裂纹宽0.002m;裂纹的位置X=a/L;裂纹的深度C=b/H。由式(4)计算[5]得到简支梁的模态频率如表1所示。

表1 简支梁的理论模态频率

由表1可以看出,当简支梁出现微小裂纹时模态频率也会发生较大的变化,利于早期裂纹的损伤检测;含有裂纹的简支梁的模态频率随着裂纹深度的的增加而减小。

3 数值模拟

根据简支梁在损伤状态下模态频率将发生变化的分析,运用ANSYSY有限元分析软件对45#钢材料的简支梁裂纹损伤情况进行模拟,并对有限元计算模拟结果进行分析。

3.1 含有裂纹的简支梁的有限元模型的建立

在ANSYS10.0平台上,建立了含有裂纹的简支梁的有限元模型。在梁的有限元分析中,选用solid45单元模拟裂纹梁,同时裂纹处采用网格加密处理(如图2所示)。

图2 裂纹加密处理

3.2 基于ANSYS对裂纹简支梁的模态分析

为了研究含裂纹梁的模态频率随裂纹位置和深度变化的规律,令完好简支梁的模态频率为ω,模态频率变化量为Δω,模态频率的变化率为η,模态阶数为r。

以模态频率的变化率来进行比较:

η=(ω-ωr)/ω×100%

(5)

在用有限元法分析计算时,分别在梁上位置X=0.1,0.2,0.3,0.4,0.5,0.6处开不同深度的裂纹,裂纹的深度从C=0.1,0.2,0.3,0.4,0.5,0.6变化。此时对36种情况分别取前四阶频率,可以得到梁在不同位置不同深度裂纹下各阶模态频率的变化(如图3所示)。

从图3(a)中可以看出来随着裂纹深度的增加模态频率的变化率从4%增加到11%,可见裂缝的深度对简支梁的模态频率影响明显。从图3可以看出模态频率的变化率都是正值,说明模态频率随着裂纹深度的增加而减小;裂纹若是在同一位置,随着裂纹深度(C=b/H)的增大,模态频率变化率也逐渐增大。若从同一裂纹深度来观察,不难看出,随着裂纹的位置变化模态频率变化率成一定的波形,这一波形跟梁的各阶振型曲线正好一致。

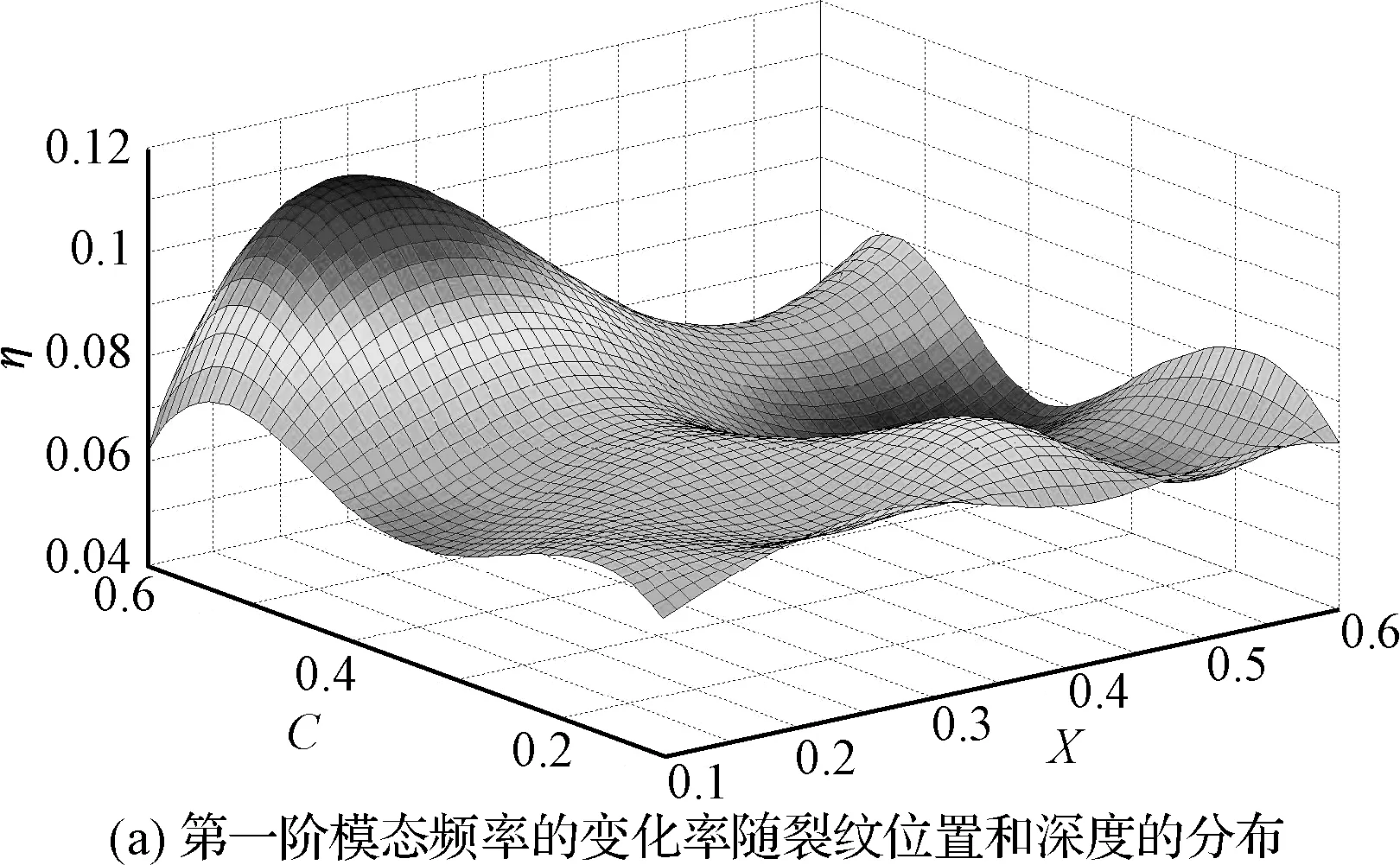
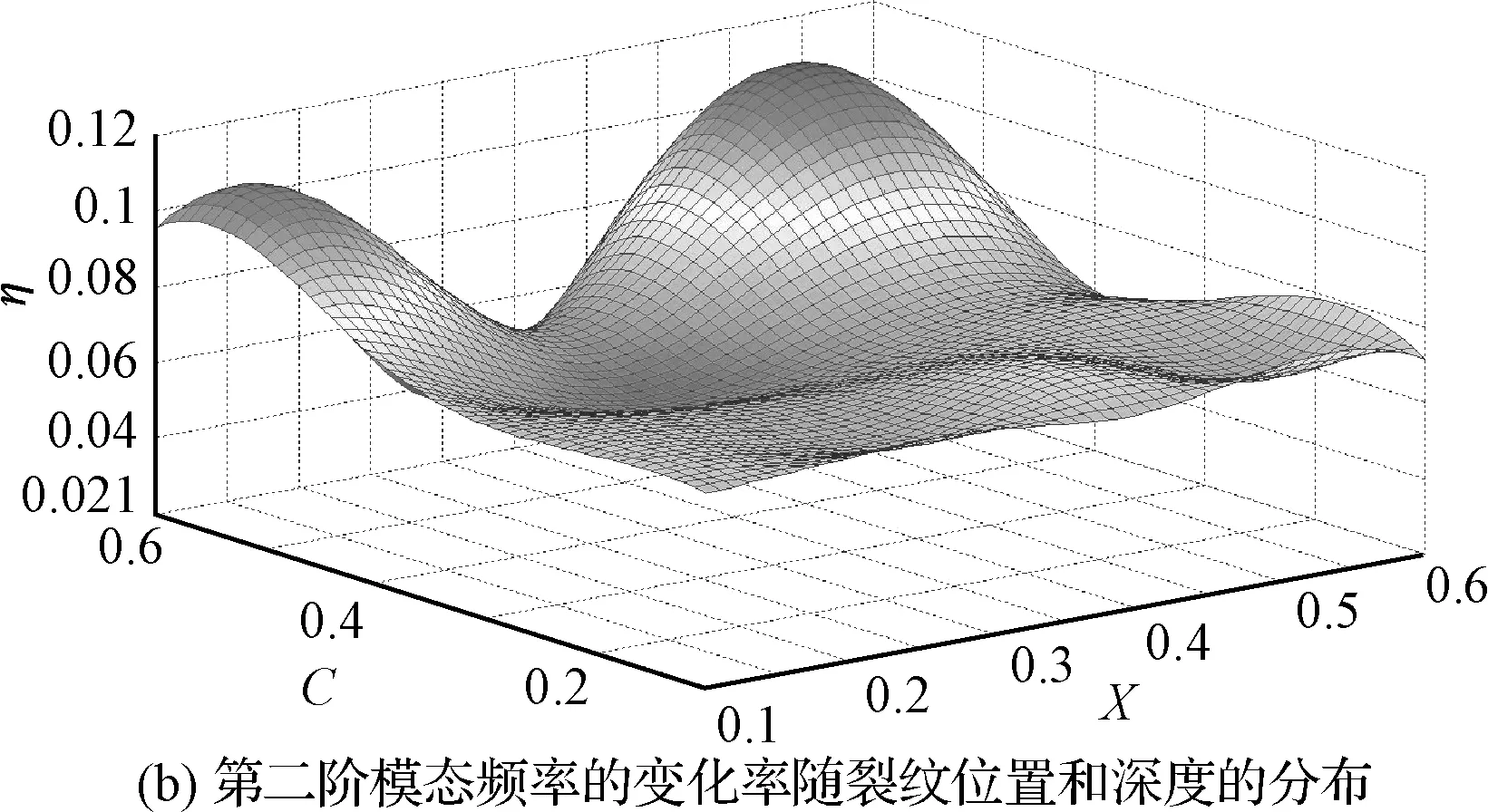
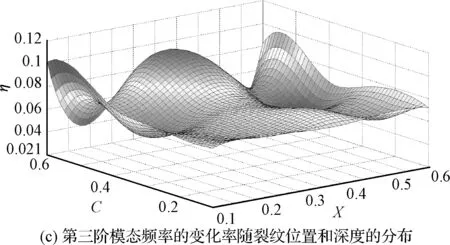
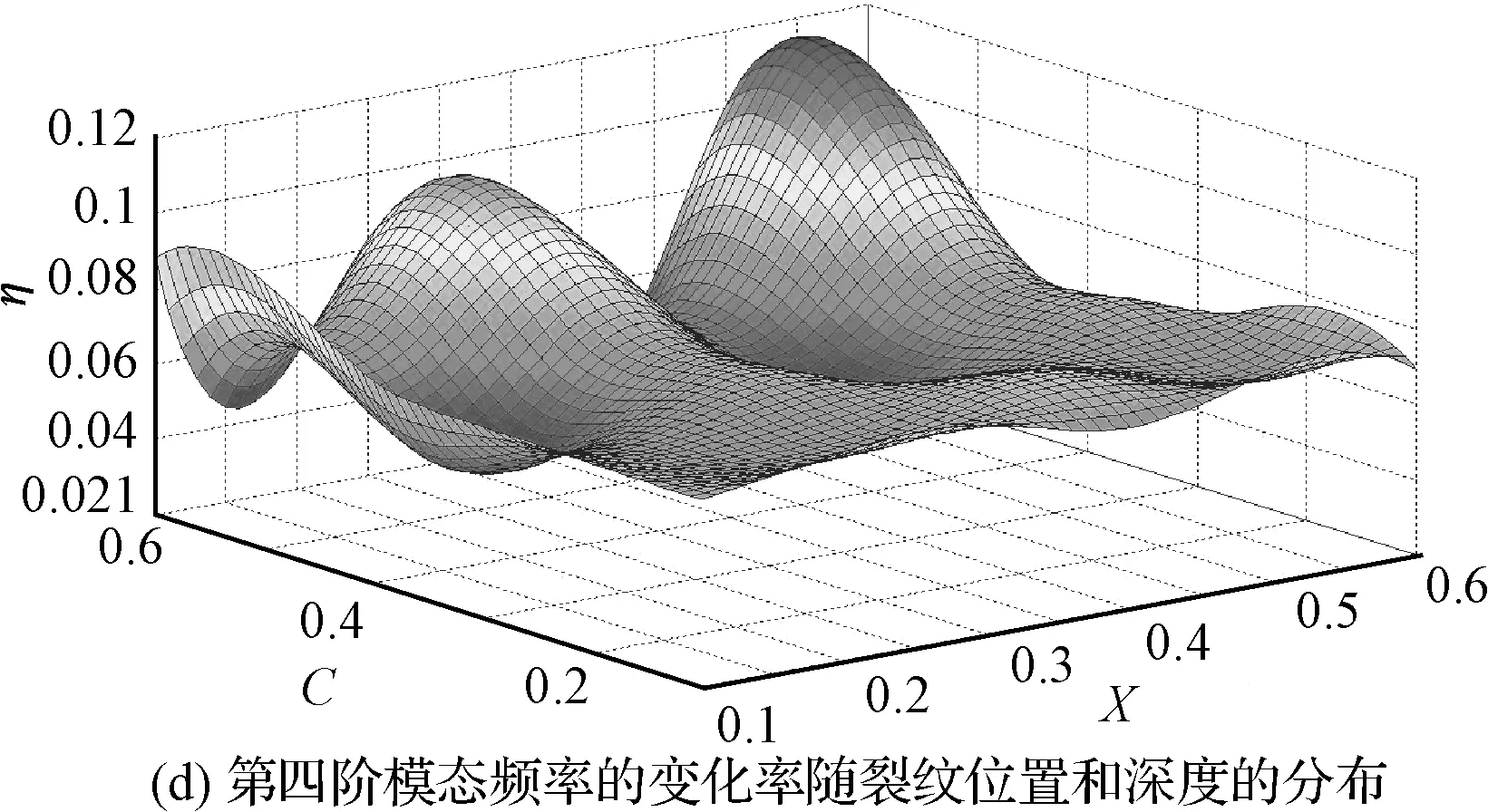
图3 简支梁模态频率的变化率随裂纹位置和深度的分布

4 实验研究

4.1 实验设备

本实验中采用的是东华测试技术有限公司生产的DH5922N动态信号测试分析系统(如图4所示),进行数据采集与存储。

图4 DH5922N动态信号测试分析系统

4.2 简支梁损伤试验方法

本实验中的振动横梁为长635mm、宽10mm、高15mm的梁,两端由螺丝固定到地上如图4所示。实验在x方向把梁分成十等份,即可以布11个测点,实验采用多点敲击、单点响应方法,在x方向顺序布置若干敲击点,裂纹确定在X=0.6处。

4.3 试验结果及分析

对裂纹在X=0.6处的简支梁分别进行损伤程度为C=0.2,0.4,0.6的试验,得到简支梁前四阶的模态频率和模态频率的变化量(如图5～图6所示),并对实验法与FEA(Finite Element Analysis)法所得模态频率进行了比较(如图7所示)。

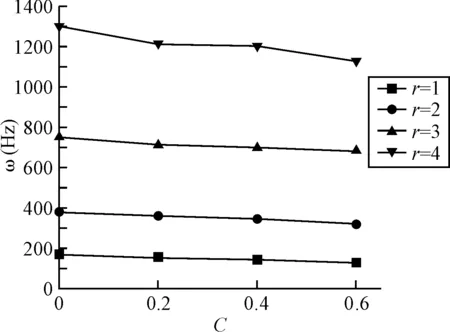
图5 简支梁前四阶的模态频率

图6 简支梁前四阶模态频率的变化量

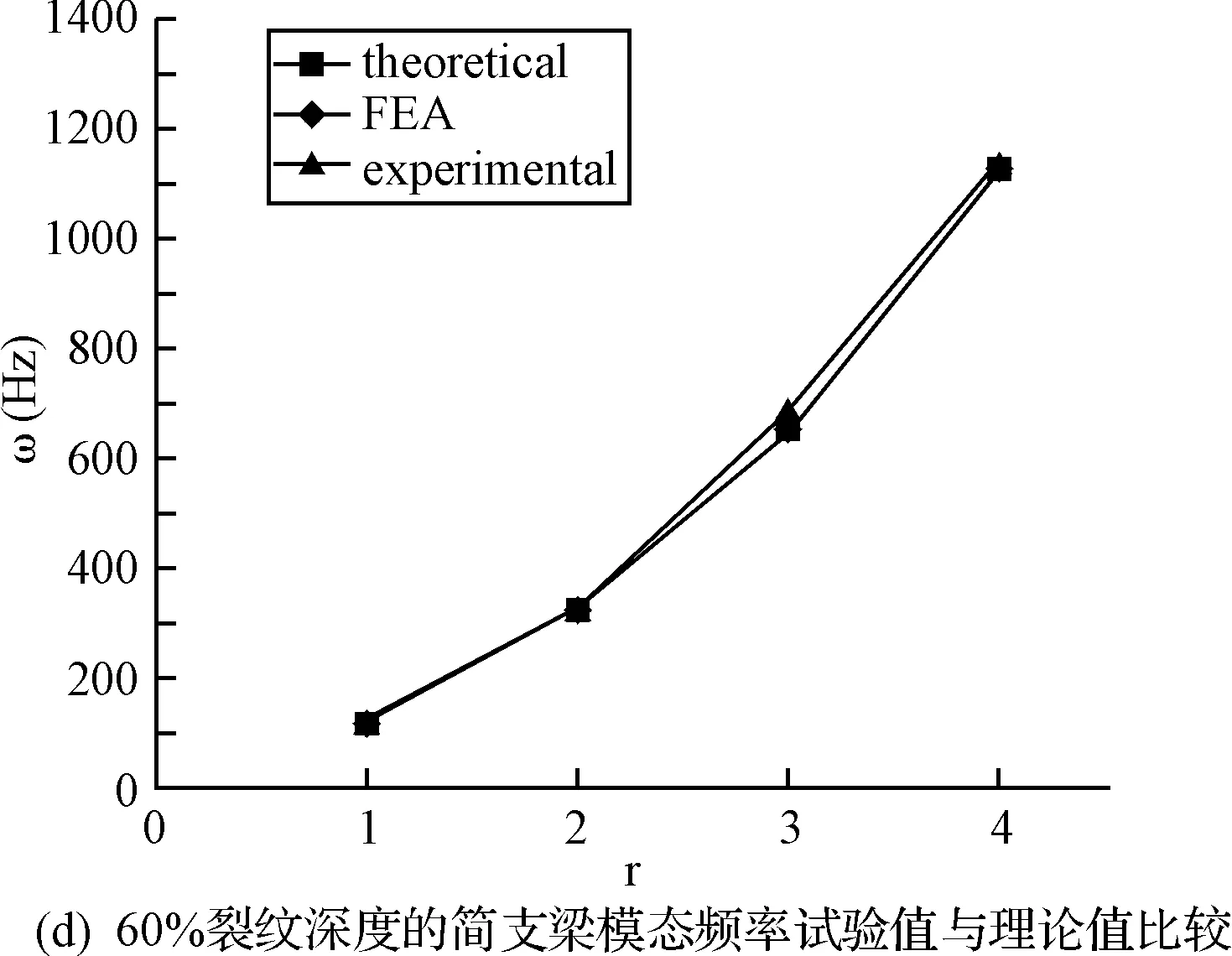
图7 简支梁模态频率试验值与理论值比较

由图5和图6可以看出简支梁的各阶模态频率随着裂纹深度的的增加而减小且变化量在增大。从图7中可以看出简支梁模态频率的理论计算值与数值模拟基本重合,数值模拟的各阶模态频率的变化趋势与试验是吻合的,说明了数值模拟和实验分析的正确性。

5 结语

1)简支梁的相对损伤从0.2增加到0.6时一阶模态频率变化量从4%增加到11%,可见裂缝的深度对简支梁的模态频率影响明显。

2)简支梁的各阶模态频率随着裂纹深度的增加而减小。

3)裂纹对模态频率的影响随着裂纹深度的增大而增大,所以,根据结构模态频率下降的多少可以诊断结构裂纹损伤的程度。

[1]王璋奇,贾建援.悬臂梁裂纹参数的识别方法[J].机械强度,2002,24(2):225-227.

[2]Stubbs N, Osegueda R.Global non-destructive damage evaluation in solids-experimentalverificaion[J].International Journal of Analytical and Experimental Modal Analysis,1990,5(3):81-97.

[3]Comwell P, Doebling S W, Farrar C R.Application of the strain energy damage detection method to platelike stractures[J].Journal of Sound and Vibration,1999,22(2):359-374.

[4]朱宏平,余璟,张俊兵.结构损伤动力检测与健康监测研究现状与展望[J].工程力学,2011,28(2):1-17.

[5]J.H.金斯伯格著.机械与结构振动—理论及应用[M].白化同,李俊宝,译.北京:中国宇航出版社,2005:26-52.

Vibration-basedDamageDetectionforCrackSimplyBeam

ZOU Zhiqiang WU Bin

(Army Officer Academy of PLA, Heifei 230031)

In view of the traditional problems of damage detection is not sensitive to early crack, crack damage detection based on vibration is studied.In this paper, the theory analysis, numerical simulation and experimental research have been carried on the crack simply beam.The results show that the modal frequency of the crack simply beam decreases with the increase of the crack depth, confirms the feasibility of crack damage detection based on modal frequency, provides the basis for the early detection of injury.

vibration, simply beam, damage detection, modal frequency

2014年3月17日,

:2014年4月18日

总装预先研究基金(编号:9140A27020313JB91395)资助。

邹志强,男,硕士研究生,研究方向:机械设计和故障诊断。吴斌,男,博士,副教授,研究方向:枪炮、机械制造和纳米表面工程。

TP39DOI:10.3969/j.issn1672-9730.2014.09.042