两种跨平台航迹精度测评方法研究*
(1.91404部队 秦皇岛 066000)(2.武汉数字工程研究所 武汉 430205)
两种跨平台航迹精度测评方法研究*
郑强1倪晋2刘颢2
(1.91404部队 秦皇岛 066000)(2.武汉数字工程研究所 武汉 430205)
跨平台航迹精度测评对多平台协同使用传感器航迹数据具有指导意义,论文介绍了相对于本平台距离/方位的测评方法(方法一)和空间距离精度的测评方法(方法二),从非线性坐标变换的角度分析了本平台位置对测评结果的影响,其中方法一的计算结果在两平台位置相差不大的情况下主要受被探测目标相对于这两个平台的方位角度差影响,方法二的计算结果则不受本平台位置的影响,因而后者更有意义。
跨平台; 航迹精度; 坐标变换; 非线性
ClassNumberTP391
1 引言
舰艇编队的作战范围不断扩大,面临的海上威胁不断增加,对多平台协同对抗和打击能力提出了更高的要求,当目标超出了本平台的探测范围之后,本平台传感器的探测精度往往不能满足精度要求,这时需要借助外部传感器,如其它水面平台的传感器、直升机或岸基的传感器等,并通过无线数据通信网络为本平台提供航迹数据[1],跨平台的航迹数据的精度测评相对于本平台传感器探测航迹的精度测评主要有以下不同:
1)跨平台航迹数据增加了将外平台探测数据转为绝对位置、并通过无线数据通信网络传输到本平台的过程。
2)增加了由绝对位置转为相对于本平台的距离/方位的过程。
3)对跨平台航迹数据的精度测评中存在新增引入误差、坐标转换等新问题。
本文主要研究了两种跨平台航迹精度的测评方法:相对于本平台的距离/方位的精度测评方法(方法一)和空间距离精度测评方法(方法二),其中前者是本平台航迹精度测评方法的推广。首先,简要介绍了这两种精度测评方法,然后就坐标转换对这两种精度测评方法的影响进行了分析,随着本平台位置的变化,方法一的测评结果也发生变化,而方法二的测评结果保持不变[1],后者对实际使用更有指导意义。
2 两种跨平台航迹精度测评方法
方法一和方法二从不同的角度分析了两种航迹精度测评方法,在两种方法中,探测平台探测到的航迹数据信息都需要先通过无线数据通信网络传输给本平台,然后再进行相关数据处理,开始测评[2]。其中探测平台记为A,本平台记为B。
如图1所示,方法一首先将无线数据通信网络输入的绝对位置、航迹数据输出的绝对位置转为相对本平台(真值)的距离、方位,再测评精度。
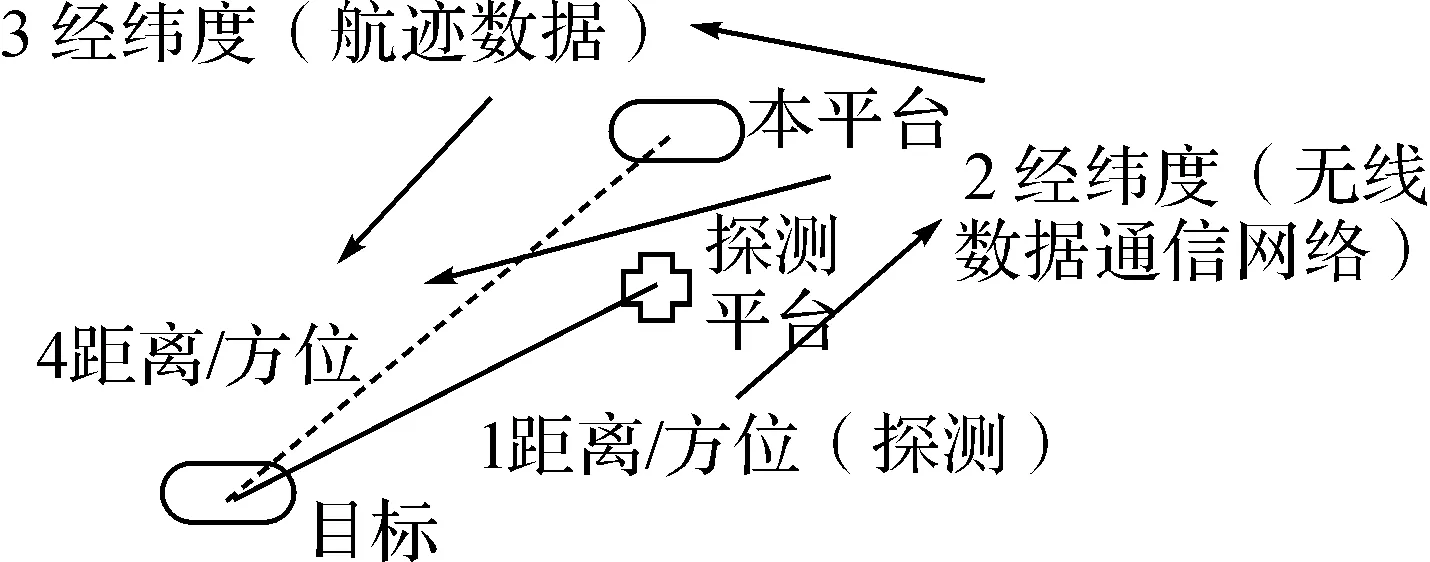
图1 方法一的坐标转换示意图
如图2所示,方法二直接比较无线数据通信网络输入的绝对位置、航迹数据输出的绝对位置与目标绝对位置(真值)之间的空间距离大小[3]。
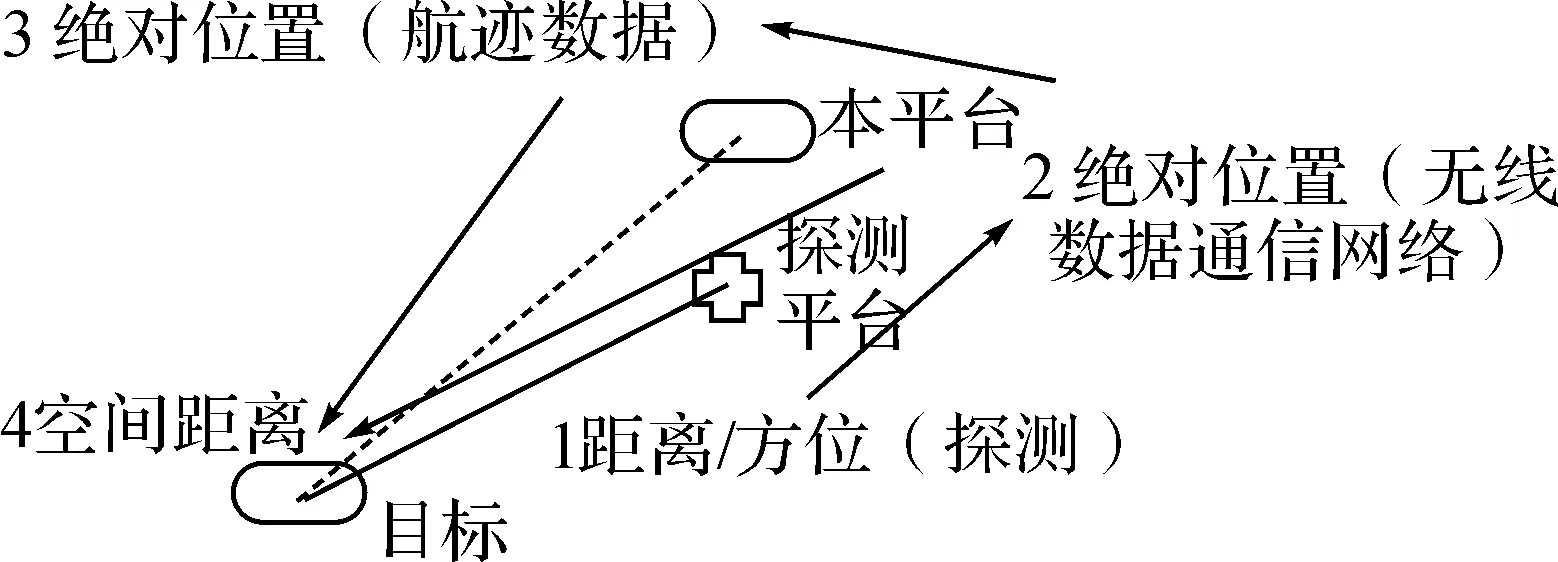
图2 方法二的坐标转换示意图
3 坐标转换对两种测评方法的影响分析
定理1:在相对本平台距离/方位的精度测评方法中[4],当A点和B点的经纬度相差不大时,雷达探测的距离误差和方位误差的测评结果由目标相对于A点和B点的角度差决定。
证明:
相对本平台距离/方位的精度测评方法分为3步,其中步骤1是由A点的雷达电轴坐标系转为当地地理坐标系,步骤2是由以A为原点的当地地理坐标系转为以B为原点的当地地理坐标系,步骤3是由当地地理坐标系转为B点的雷达电轴坐标系[5]。
测量值减去真值称为误差,这里,以随机变量xA,m表示A雷达电轴坐标系方位方向的误差,相应地,以yA,m表示距离方向的误差,以zA,m表示仰角方向的误差,xA,m、yA,m、zA,m均满足均值为零的正态分布。同时,以随机变量xA,t表示以A为原点的当地地理坐标系中东西方向的误差,以yA,t表示南北方向的误差,以zA,t表示天向的误差,将目标量测在真值处泰勒展开,保留一阶项,那么对步骤1近似有[6]:
其中,βA表示目标相对于A点的方位,εA表示目标相对于A点的仰角,对二维雷达εA=0,那么有:
以随机变量xB,t表示以B为原点的当地地理坐标系中东西方向的误差,相应地,以yB,t表示南北方向的误差,以zB,t表示天向的误差,与步骤1类似对误差计算式进行泰勒展开,保留一阶项,那么对步骤2近似有:
其中Δλ=λA-λB。
在实际试验中,由于A点与B点的经纬度相差不大,因此:
sin(Δλ)≈0,cos(Δλ)≈1,sin(Δφ)≈0,cos(Δφ)≈1
因此:
以随机变量xB,m表示B雷达电轴坐标系方位方向的误差,相应地,以yB,m表示距离方向的误差,以zB,m表示仰角方向的误差,与步骤1类似对误差计算式进行泰勒展开,保留一阶项,那么对步骤3近似有:
其中,βB表示目标相对于B点的方位,εB表示目标相对于B点的仰角,对二维雷达εA=0,那么有:
总之,合并步骤1、步骤2、步骤3后,可得:
得证。
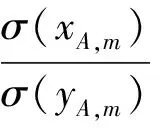
证明:
xA,m与yA,m是独立均值为零的正态分布,那么其线性组合xB,m与yB,m仍为均值为零的正态分布,可得:
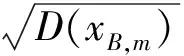
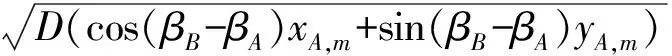
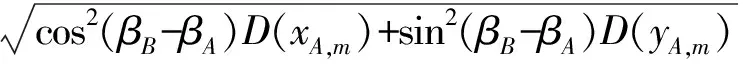
由于:
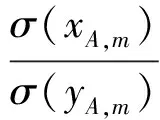
代入得
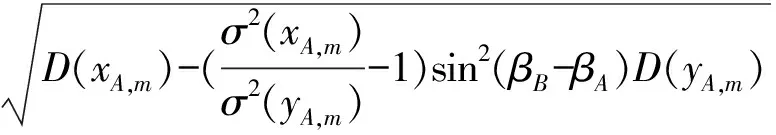
≤σ(xA,m)
又βB-βA不恒为零,故
σ(xB,m)<σ(xA,m)
(3)
由积分中值定理,存在dB,m和dA,m,使得
dB,mσ(βB,m)=σ(xB,m)<σ(xA,m)=dA,mσ(βA,m)
其中dB,m表示目标在以B为原点的极坐标系的距离,βB,m表示目标在以B为原点的极坐标系的方位,dA,m表示目标在以A为原点的极坐标系的距离,βA,m表示目标在以A为原点的极坐标系的方位。本次试验中,目标相对于本平台的距离均大于目标相对于直升机的距离,有:
dB,m>dA,m
因此,有:
σ(βB,m)<σ(βA,m)
(4)
同理可得:
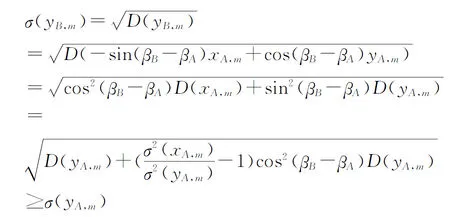
又βB-βA不恒为零,故
σ(yB,m)>σ(yA,m)
(5)
由式(3)~式(5)可知,推论成立。
定理2:在空间距离精度测评方法中,空间距离误差不变。
证明:
以C表示目标位置,经度为λC,纬度为φC,D表示测评原点(任意选取),经度为λD,纬度为φD,由C到D的当地地理坐标系转换矩阵即为M3。
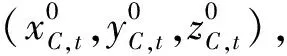
空间距离误差在以C为原点的当地地理坐标系中表示为EC,相应地在以D为原点的当地地理坐标系中表示为ED,则:
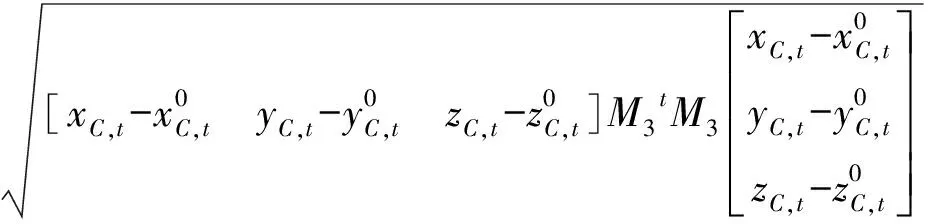
由MCD为单位正交阵,得:
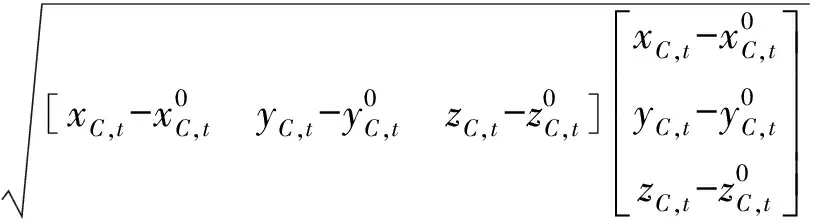
得证。
4 结语
综上所述,方法一的测评结果随本平台相对目标的位置不同而发生改变,受坐标变换影响较大,在平台不停变换的过程中,需要对测评数据进行反复验算,增加了工作量。而在方法二中,空间距离精度是一个绝对值,不随本平台相对目标位置变化,无论本平台位置如何变化,测评结果意义明确,大小不变。方法二对航迹精度的测评比较科学,测评结果与舰弹指标、无线数据通信网络误差表示方式比较一致,对实际的使用更具有指导意义。
现阶段对单平台航迹精度测量的研究还比较多,为航迹精度的测量提供了丰富的经验,但对于跨平台的航迹精度测评的研究相对较少,本文从坐标变换的角度简要揭示了两种跨平台航迹精度测评方法的优劣,但在实际测评中仍然有大量的问题需要解决和完善,希望通过文章能在一定的程度上对航迹精度的测评方法未来的的选择和发展提供参考。
[1]刘镝,黄颖,王飞.多平台条件下目标指示精度分析方法[J].舰船电子对抗,2011,34(4):19-21.
[2]丁鹭飞.雷达原理[M].西安:西安电子科技大学出版社,2002:125-126.
[3]江言林,刘辉建.探测平台目指精度对反舰导弹捕捉效能影响分析[J].指挥控制与仿真,2007,29(4):59-62.
[4]刘基余.GPS卫星导航定位原理与方法[M].北京:科学出版社,2003:432-434.
[5]Y.Bar-Shalom, W.D.Blair, et al.Multitarget-Multisensor Tracking: Applications and Advances Ⅲ[M].London: Atech House Inc.,2000:25-26.
[6]杨万海.多传感器数据融合及其应用[M].西安:西安电子科技大学出版社,2004:53-54.
[7]韩崇昭,朱洪艳,段战胜.多源信息融合[M].北京:清华大学出版社,2006:325-326.
[8]Merrill I.Skolnik.雷达手册[M].第二版.北京:电子工业出版社,2003:212-213.
[9]王小非.C3I系统中的数据融合技术[M].哈尔滨:哈尔滨工程大学出版社,2006:92-93.
[10]何友.多传感器信息融合及应用[M].北京:电子工业出版社,2000:225-226.
TwoEvaluationMethodsofCross-platformTrackingAccuracy
ZHENG Qiang1NI Jin2Liu Hao2
(1.No.91404 Troops of PLA, Qinhuangdao 066000)(2.Wuhan Digital Engineering Institute, Wuhan 430205)
The evaluation of cross-platform tracking accuracy has guiding significance in cooperatively using multiplatform sensors tracking data.The measurement method using distance/azimuth to the base platform to evaluate the tracking accuracy(Method one)and the other method using space distance to evaluate the tracking accuracy(Method two)are introduced, and the influence of platform position on the evaluation result in the perspective of nonlinear coordinate transform is analyzed.The evaluation result of method one is mainly affected by the difference of the azimuth and angle when two platforms were in a certain area, the evaluation result of method two is not affected by the platform position.
cross-platform, tracking accuracy, coordinate transform, nonlinear
2014年3月7日,
:2014年4月16日
郑强,男,工程师,研究方向:舰艇指控系统工程与评测。倪晋,男,硕士研究生,研究方向:信息融合。刘颢,男,工程师,研究方向:信息融合,偏微分方程。
TP391DOI:10.3969/j.issn1672-9730.2014.09.034

