固化疏浚泥双层地基承载力颗粒流数值模拟

王晓琳，刘文白，吴丽颖，高开仙，黄晓健

(1.上海海事大学海洋科学与工程学院，上海 201306;2.上海港湾工程质量检测有限公司，上海 201315)

0 引言

近年来，固化技术从日本等地引进，并在一些沿海地区得到广泛应用.［1]将该技术应用到围填海工程中，既能提高疏浚泥地基的强度，使得在疏浚泥或软弱土层上覆有固化土层的人工双层地基满足一定的承载力要求，又能大量节省工程中软土地基处理时间，在短时间内为后续地基处理提供一个施工平台.［2-4]若能在软土地基处理中，充分发挥其上覆固化层的良好的物理力学特性和抗变形能力，就可以有效地控制和减小软土地基的沉降量，提高软土地基的稳定性.［5-7]王宁伟等［8]对固化软土双层地基承载性能进行试验研究;刘文白等［9-11]通过室内试验、数字照相变形量测(Digital Photogrammetry for Deformation Measurement，DPDM)技术、ABAQUS数值模拟等方法对固化双层地基承载性能进行较为系统的研究.

本文根据固化疏浚泥双层地基承载性室内模型试验，利用颗粒流程序PFC2D进行数值模拟，研究不同强度、厚度的固化层和厚宽比(固化层厚度与基础宽度的比值)对固化疏浚泥双层地基承载性和破坏形式的影响，并与室内试验结果进行对比分析.

1 室内模型试验

1.1 试验材料

试验所用土取自上海临港新城东海岸附近吹填的疏浚泥，经颗粒分析试验结果判定，该土为粉土［12]，具体物理力学性质指标见表1.

表1 疏浚泥的物理力学性质指标

试验所用的固化剂为PM固化剂.PM固化剂主要由一种胶结物和激发剂组成.其中激发剂的主要成分是木质素，它是由聚合的芳香醇构成的一种复杂酚类聚合物，对提高拌合物保水性、和易性，短时间内增加其强度和颗粒之间的内聚力有良好的效果.

1.2 试验方法

为研究固化疏浚泥双层地基中上层固化层厚度H，固化剂配合比λ和厚宽比对上层固化层承载性的影响，在室内进行固化疏浚泥双层地基模型试验.试验装置见图1.试验装置主要包括模型箱和加载装置.模型箱采用方形三角铁框架和玻璃墙体，其长48 cm，宽 28 cm，高30 cm;加载装置包括千斤顶和量力环.底面基础为方形基础，其尺寸为30 mm×30 mm.

图1 双层地基模型试验装置

室内模型试验共有18组.针对本次颗粒流数值模拟，选取H分别为30 mm，45 mm，60 mm的3组试验数据，λ分别为4%和5%的2组试验数据进行对比.试验中采用外掺法确定固化剂掺量.具体试验方案见表2.

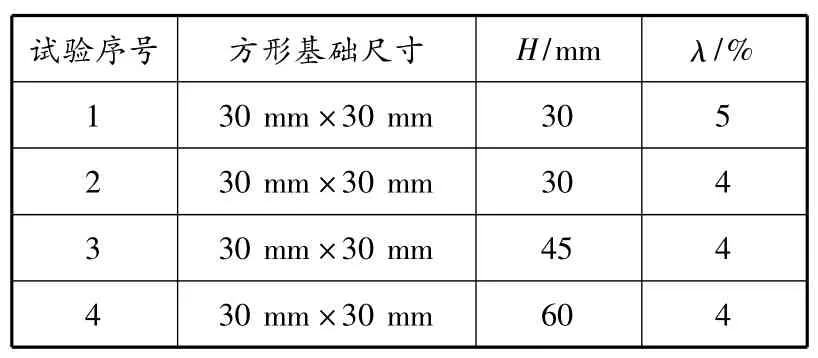
表2 试验方案

1.3 试验结果

室内模型试验中上层固化层在不同强度和厚度条件下所得的极限承载力见表3.双层地基的破坏形式为整体剪切破坏，增加λ可以有效提高双层地基的极限承载力，且效果比增加H显著.方形基础下的厚宽比与极限承载力成线性关系.

表3 双层地基的极限承载力室内模型试验结果

2 模型试验的颗粒流数值模拟

本文应用颗粒流程序PFC2D建立4个二维模型，分别模拟30 mm×30 mm基础条件下H分别为30 mm，45 mm，60 mm的双层地基和60 mm×60 mm基础条件下H为60 mm的双层地基.

2.1 颗粒流模型的建立

在固化疏浚泥双层地基颗粒流数值模型建立过程中，首先定义墙体模拟模型箱，共4道墙.在实际试验中模型箱的长、宽、高分别为48 cm，28 cm，30 cm;在数值模拟模型中，模型箱几何坐标为(0，0)，(28，0)，(28，30)和(0，30)，宽 28 个单位、高 30个单位.接着在上述给定的墙体范围内生成颗粒(约4 500颗)，按颗粒间无重叠的方式将颗粒随机填充至区域内，循环步数为3 000步，最后在重力的作用下经过一定的循环达到平衡，生成地基土模型.其中，形成上层固化层的圆形颗粒采用黏结模型，具有一定的强度和刚度，下层疏浚泥则由一般圆形颗粒组成，颗粒间的相互作用采用线性接触刚度模型.

待地基土颗粒平衡后，删除上面的墙wall 3，然后利用“macro”命令生成基础.室内试验中30 mm×30 mm的方形基础在数值模拟中采用宽和高均为3个单位的聚粒模拟，60 mm×60 mm的方形基础采用宽6个单位、高3个单位的聚粒模拟.图2为模拟的模型箱及箱内土体和基础经自平衡后达到的模拟试验加载前的状态.具体的数值模拟方案见表4.

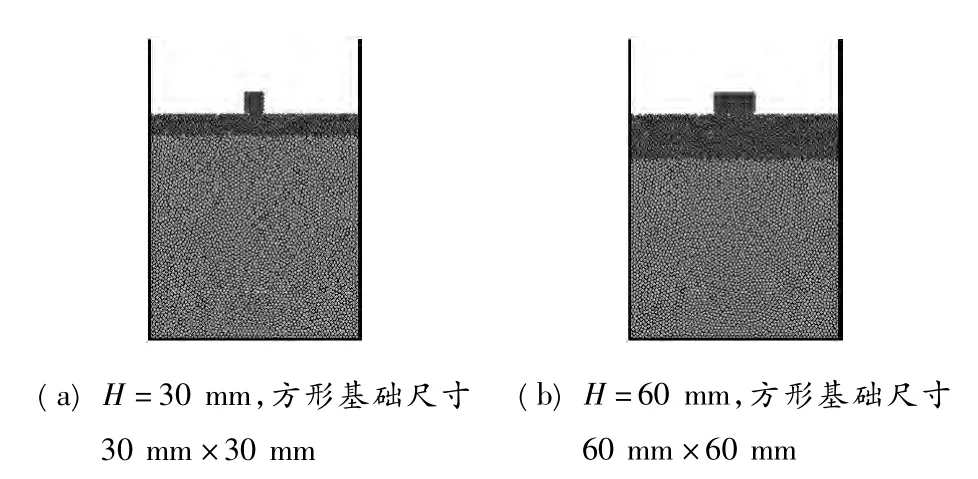
图2 方形基础作用下的双层地基模型

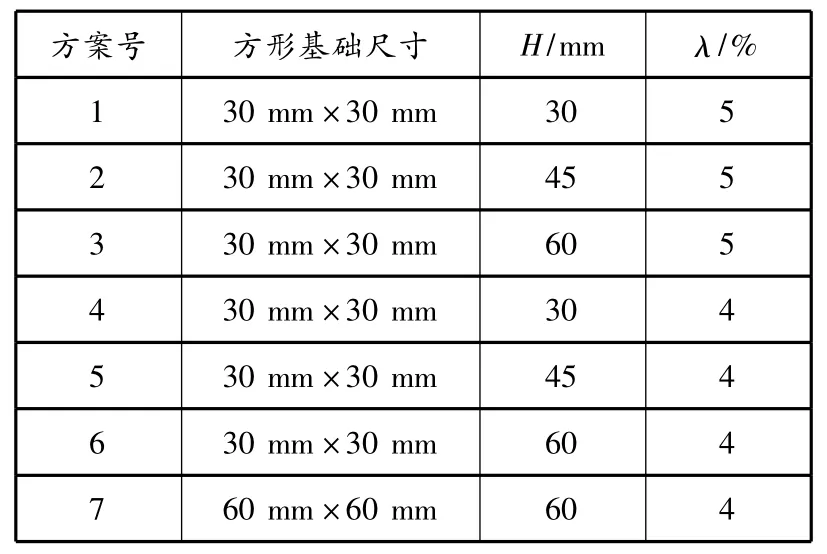
表4 数值模拟方案

在数值模拟中，颗粒流模型的参数见表5.需要指出的是，表5中所列的颗粒刚度、摩擦因数、颗粒间黏结强度和颗粒密度指标为颗粒流数值模拟的介质颗粒的自定义指标，而不是真实的试验土体颗粒的物理指标.［13-14]

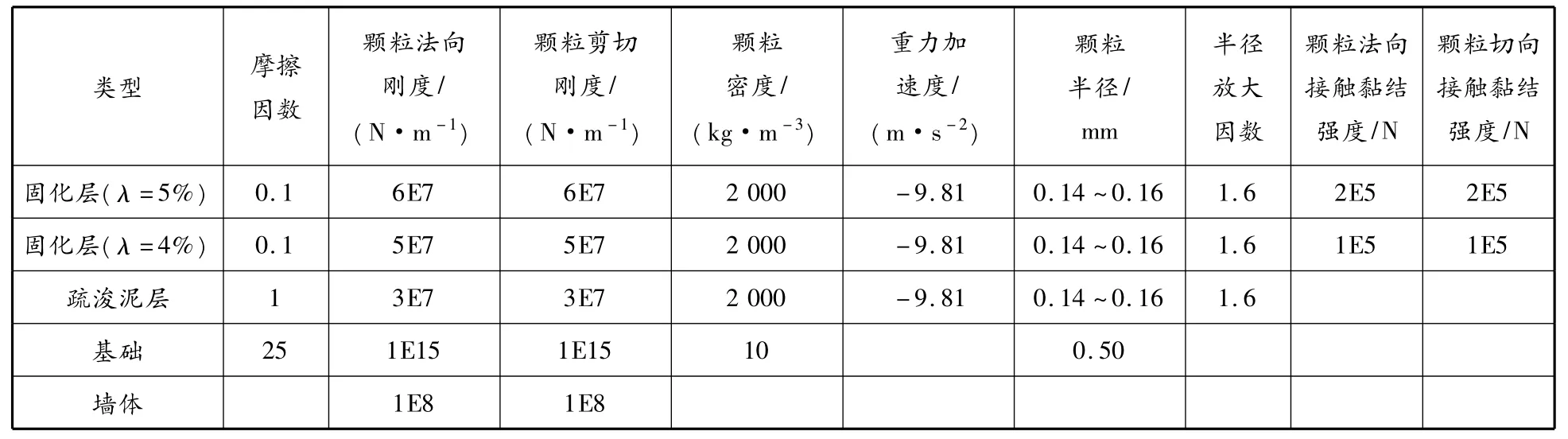
表5 颗粒流模型基本参数

模拟中通过程序命令模拟加载过程，载荷p作用在基础上，载荷分级加载，每级载荷50 kPa.利用“hist”命令跟踪基础底层颗粒，获得其位移历史曲线，从而得到载荷与位移关系曲线，与室内模型试验结果进行对比分析.

2.2 数值模拟结果和分析

2.2.1 地基的破坏形式分析

图3是固化疏浚泥双层地基在不同载荷作用下的颗粒变化分布.比较图3(a)～3(d)发现:当p=50 kPa时，地基土颗粒的排列未发生显著变化，土表面近似水平;当 p增加到100 kPa时，基础略微下降，固化疏浚泥层未遭破坏，土表面呈弧线下凹状态，此时为固化疏浚泥双层地基承载的弹性阶段;当p增加到150 kPa后，基础慢慢下沉，固化层土颗粒孔隙减小，密实程度增加，但上层固化层与下层疏浚泥层的交界面未出现显著变化，此时为固化疏浚泥双层地基承载的弹塑性阶段;当 p继续增加到200 kPa时，上层固化层变形加剧，基础及其下层疏浚泥层急剧下沉，土体颗粒出现破坏面，上层固化层颗粒越过上下层交界面进入到下层疏浚泥层中，此时为固化疏浚泥双层地基承载的破坏阶段.

图3 H=30 mm时颗粒变化分布

图4 是当H=45 mm和λ=4%时的双层地基在不同载荷状态下的颗粒接触力分布.图中黑线表示颗粒间力的大小和方向，黑线越粗表示颗粒间接触力越大.在模拟加载过程中，地基土颗粒随p的增加不断发生位移和旋转，颗粒间接触力不断发生变化.比较图4(a)和4(b)发现，随着p的增加，基础下部地基与固化层土颗粒间的黑线变粗(接触力变大)，基础周围的应力越来越集中，且黑粗线的位置逐渐下移至疏浚泥层，疏浚泥层颗粒间的接触力增大.当p=100 kPa时，固化疏浚泥双层地基处于弹性阶段，由上层固化层承担全部载荷;当p=300 kPa时，固化疏浚泥双层地基处于破坏阶段，由上层固化层和下层疏浚泥层共同承担载荷.

图4 H=45 mm，λ=4%时颗粒接触力分布

通过分析各级载荷作用下颗粒的疏松部位、颗粒速度值的突变位置、颗粒间接触力的突变位置及受影响区域，可以得出:基础在竖直载荷作用下发生整体刺入地基的破坏，固化层土体在基础刺入作用下向疏浚泥层扩散，出现整体剪切破坏.［15]

2.2.2 双层地基承载力影响因素分析

影响固化疏浚泥双层地基承载力的因素较多.前期研究结果表明，固化疏浚泥双层地基的承载力主要取决于H，λ和厚宽比.因此，对室内模型试验进行颗粒流数值模拟，通过各级载荷下颗粒的分布、速度、位移和接触力，分析加载过程中颗粒的细观结构变化，研究H，λ和厚宽比对固化疏浚泥双层地基承载力的影响规律.

比较图3(d)和3(e)发现，在相同载荷 p=200 kPa作用下，λ=4%时H=30 mm的双层地基上的基础有一定沉降，固化层表面出现破坏面，上层固化层土体颗粒向下层疏浚泥层扩散，而λ=5%时H=30 mm的双层地基颗粒排列无明显变化，基础下方的颗粒相对比较密实.因此，λ=5%的双层地基比λ=4%的双层地基的承载力更大.

图5是不同固化层厚度的固化疏浚泥双层地基在λ=4%，p=200 kPa时的颗粒速度分布.图中箭头的长短表示速度值的大小，点表示速度值极小或为零.颗粒速度值较大的区域为受影响区域.由图5可知:H为30 mm的双层地基在p=200 kPa作用下，地基土体丧失承载能力，基础下陷，受影响区域范围较小而破坏面边界明显;H为45 mm的双层地基在相同载荷作用下，地基土体未达到破坏状态，地基表面出现细微裂缝，受影响区域越过双层地基交界面延伸至下层疏浚泥层，疏浚泥层对地基承载力提供贡献;H为60 mm的双层地基在相同载荷作用下，受影响区域主要在上层固化层，双层地基处于弹性阶段，载荷由上层固化层承担.

图5 λ=4%，p=200 kPa时颗粒速度分布

结合表6中数值模拟得到的双层地基极限承载力表明:(1)当λ=4%时，随着H的增加，固化疏浚泥双层地基承载力不断增大.当H从30 mm增加到45 mm时，固化疏浚泥双层地基极限承载力增加33%.(2)当H相同时，固化疏浚泥双层地基承载力随λ的增加明显增大.当λ从4%增加到5%时，H为30 mm的固化疏浚泥双层地基的极限承载力增加56%.观察图6中30 mm×30 mm基础条件下H为30 mm的双层地基(模拟方案4)和60 mm×60 mm基础条件下H为60 mm的双层地基(模拟方案7)在模拟加载过程中得到的载荷-位移曲线，发现上述两种条件下的双层地基的载荷-位移曲线基本吻合，表明固化疏浚泥双层地基的厚宽比相同时，其双层地基承载力近似.图7为30 mm×30 mm基础条件下的厚宽比与极限承载力的关系曲线.观察图6发现，极限承载力与厚宽比成线性关系.当厚宽比大于1.5时，λ分别为4%和5%的曲线斜率开始增加.随着宽厚比的增加，两种λ的双层地基的极限承载力差值不断增大.宽厚比从1.0增加到2.0时，λ为4%的双层地基极限承载力增加83%.

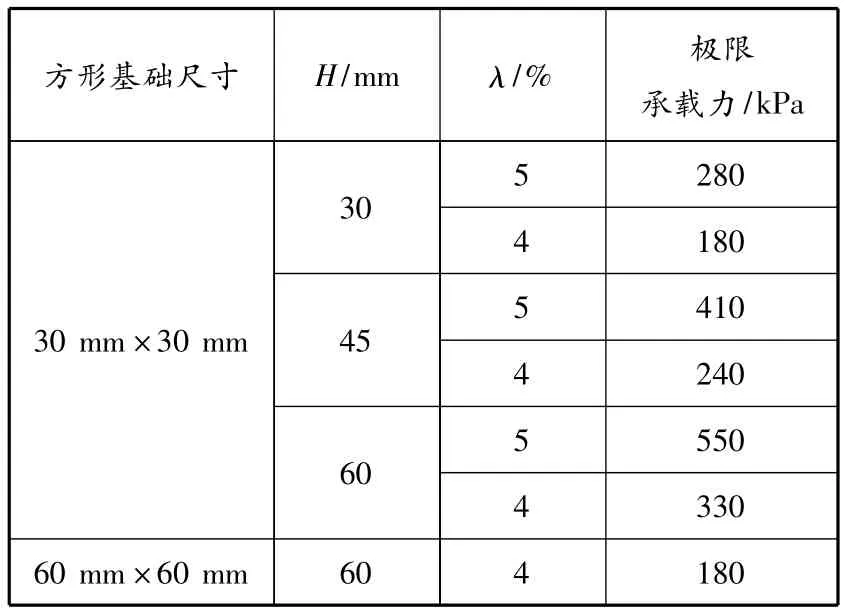
表6 双层地基极限承载力数值模拟结果

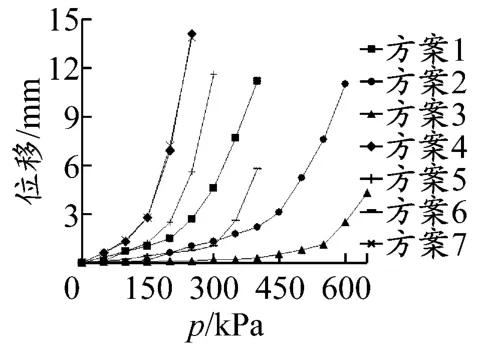
图6 载荷-位移曲线

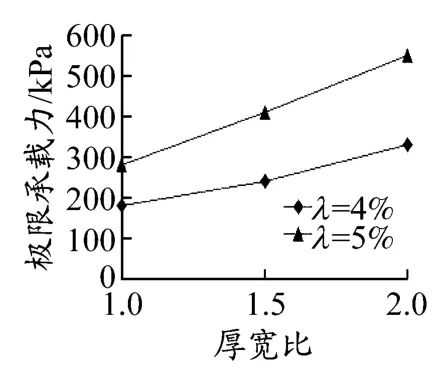
图7 厚宽比与极限承载力关系

2.3 颗粒流数值模拟与室内模型试验结果的对比

在颗粒流数值模拟加载过程中，利用“hist”命令跟踪基础底层颗粒的位移(见图6)，得到5条载荷-位移曲线，并以H和λ为变化量进行分析比较.

采用《土工试验方法标准》［16]中的拐点法和双切法综合确定极限承载力.表6所示为按上述原则在图6中载荷-位移曲线上找到的特征点所对应的载荷，即极限承载力.

将表6的数据与室内模型试验的数据进行对比，发现两者吻合度较高:当λ=4%时H分别为30 mm，45 mm和60 mm固化疏浚泥双层地基的极限承载力分别与室内模型试验结果相差1.7%，6.2%和4.4%;当λ =5%时 H 为30 mm的固化疏浚泥双层地基的极限承载力与室内模型试验结果相差1.2%.两种方法得到的双层地基的极限承载力在数值上相接近，吻合度较高，因此可以通过颗粒流数值模拟对固化疏浚泥双层地基进行细观结构研究.

3 结论

(1)固化疏浚泥双层地基承载过程为弹性-弹塑性-破坏三个阶段，其破坏形式为整体剪切破坏.

(2)随着固化疏浚泥双层地基上层固化层H和λ的增加，固化疏浚泥双层地基承载力随之逐渐增加.当H从30 mm增加到45 mm时，λ为4%的固化疏浚泥双层地基极限承载力增加23%;当λ从4%增加到5%时，H为30 mm的固化疏浚泥双层地基极限承载力增加51%.

(3)增加固化疏浚泥双层地基的厚宽比可以提高地基承载力.当厚宽比从1.0增加到2.0时，λ为4%的固化疏浚泥双层地基极限承载力增加51%.

(4)颗粒流数值模拟结果表明:当竖直载荷较小时，双层地基颗粒的排列分布未发生显著变化;当载荷逐步增加至极限承载载荷时，基础不断下沉，固化疏浚泥双层地基表面从出现细微裂缝逐渐发展至出现明显的颗粒排列疏松区.随着载荷的增加，颗粒的速度值突变区域的范围逐渐减小，而区域边界逐渐明显，该边界可作为判定固化疏浚泥双层地基破坏面的依据.

［1]王建平，顾文萍，王健祥，等.淤泥固化土技术在连云港徐圩港区软土地基中的应用［J].水运工程，2013(10):198-202.

［2]王东星，徐卫亚.固化淤泥长期强度和变形特性试验研究［J].中南大学学报:自然科学版，2013，44(1):332-339.

［3]丁毅，李乃军.应用于粉砂土的土壤固化剂性能及机理分析［J].中国建材科技，2013(3):46-63.

［4]刘青松，张春雷，汪顺才，等.淤泥堆场人工硬壳层地基极限承载力室内模拟研究［J].岩土力学，2008，29(S1):667-670.

［5]MEYER G G，HANA A M.Design charts for ultimate bearing capacity of foundations on sand overlying soft clay［J].Canadian Geotechnical J，1980，17(2):300-303.

［6]问延煦.双层地基承载与变形特性研究［D].上海:同济大学，2007.

［7]彭月明，张铁壮，窦远明.硬壳层对软土地基沉降特性影响的研究［J].河北工业大学学报，2007，36(1):101-105.

［8]王宁伟，高园，王玉梅.固化软土地基的室内平板载荷试验［C]//第八届沈阳科学学术年会论文集，2011:447-451.

［9]刘文白，魏晓添，赵玉同.软黏土上覆硬土层极限承载力室内模型试验研究［J].水运工程，2011(5):119-123.

［10]刘文白，黄晓健，魏晓添，等.基于DPDM技术的室内双层地基承载试验及变形场分析［J].水运工程，2011(8):133-138.

［11]刘文白，蒋宏鸣，刘春林，等.固化软土双层地基室内模型试验数值模拟研究［J].水运工程，2012(11):173-178.

［12]GB/T 50145—2007，土的工程分类标准［S].

［13]周健，池永，池毓蔚，等.颗粒流方法及PFC2D程序［J].岩土力学，2000，21(3):271-274.

［14]刘文白，周健.上拔载荷作用下桩的颗粒流数值模拟［J].岩土工程学报，2004，26(4):516-521.

［15]梁永辉.上覆硬壳层软土地基的工程特性试验研究及数值分析［D].上海:同济大学，2007.

［16]GB/T 50123—1999，土工试验方法标准［S].