永磁同步电机调速的预测电流控制方法

周左晗，李腾飞，施伟锋

(上海海事大学物流工程学院，上海 201306)

0 引言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)以其结构简单、体积小、重量轻、损耗小、效率高等特点，广泛应用于国防、工农业生产和日常生活等各个方面，目前正向大功率、高功能和微型化的方向发展.PMSM大多采用直接转矩控制方法调速，仅根据已知矢量表进行控制，一般不对系统未来采样时间内可能产生的负载电流进行预测.［1-6]此外，直接转矩控制中的滞环控制器导致开关频率变化，当测量值与参考值的误差大于限定阈值时进行一次控制以减小误差，但在后续控制中误差可能再次超出阈值.长时间的控制计算会导致转矩和磁通超出滞环限制.［7]

采用预测电流控制方法对PMSM进行调速可解决上述问题.电机调速系统中三相脉冲宽度调制(Pulse Width Modulation，PWM)逆变器对电流的控制有一个周期延迟，预测电流控制的思想是在一个PWM周期内实现实际电流趋近并最终等于参考电流，具体方法是在每个周期内选取与参考电流误差最小的电流控制电压矢量，预测性地控制电流矢量.［8-12]预测电流控制实时优化开关配置，每次选择配置可以控制电流矢量轨迹相对于参考电流矢量轨迹保持最小的空间误差，并在未来的每个采样计算周期内重新选择配置状态，实时减小电流矢量误差.［13]预测电流控制能在尽可能短的时间内高精度地控制定子电流，这使得PMSM调速系统的动态性能更佳、谐波影响更低.

1 PMSM建模

1.1 PMSM数学模型

PMSM的三相绕组分布在定子上，永磁体安装在转子上.PMSM运行时定子与转子始终处于相对运动状态，永磁体与绕组以及绕组之间的相互影响使得电磁关系十分复杂，再加上磁路饱和等非线性因素，很难建立 PMSM精确的数学模型.为简化PMSM数学模型，假设:(1)忽略电机的磁路饱和，认为磁路是线性的;(2)不考虑涡流和磁滞损耗;(3)当定子绕组加上三相对称正弦电流时，气隙中只产生正弦分布的磁势，忽略气隙中的高次谐波;(4)开关管和续流二极管为理想元件;(5)忽略齿槽、换向过程和电枢反应等影响.［14]

PMSM的数学模型主要由电压方程、磁链方程和转矩方程组成，为简化运算、便于建模，采用两相旋转d-q坐标系下的数学模型，并通过坐标变换得到三相静止a-b-c坐标系下的方程.

PMSM在d-q坐标系下的电压方程为

式中:Rs为定子电阻;ud和uq分别为d和q轴的相电压;id和iq分别为d和q轴的相电流;Ld和Lq分别为d和q轴的电感;Ψd和Ψq分别为d和q轴的磁通;ω为电角速度.

由于d-q轴不是由真实物理量组成的坐标轴，在仿真试验中通过坐标变换得到a-b-c坐标系下的电压方程

式中:ua，ub，uc分别为 a，b，c轴的相电压;θ为 d-q坐标系与a-b-c坐标系之间的电角度.

永磁同步电机的磁链方程为

式中:Ψf为永磁转子产生的磁链.

永磁同步电机的转矩方程为

式中:p为电机的极对数.

把式(3)代入式(4)可得

式中等号右侧:第1项是定子电流和永磁体产生的转矩，称为永磁转矩;第2项是转子凸极效应引起的转矩，称为磁阻转矩.若Ld=Lq，则不存在磁阻转矩且永磁体磁链为常数，此时电机转矩只与iq有关，转矩方程简化为

1.2 PMSM模型离散化

离散化PMSM模型是为降低连续系统的时间复杂度，实现离散时间内的信号采样，为电流预测控制作理论准备.

根据式(1)可得PMSM在d-q坐标系下的状态方程

设Ld=Lq=Ls，可以推出

式中:Rs，Ls和Ψf为与时间无关的常数.

利用泰勒公式的一阶展开，得到PMSM模型的离散化方程［15]

为便于实现离散模型，需排除d，q轴电流的耦合效应.在仿真过程中选取满足香农采样定理的足够小的采样时间T，从而可以忽略采样时间内电机的旋转角度.因此，可以忽略矩阵F和H中T与ω相乘的项.

1.3 逆变器及其电压矢量

PMSM的驱动电流为三相相差120°的正弦电流，目前常用MOSFET或IGBT等电力电子器件构成的三相逆变电路对其进行矢量控制.三相电压型逆变器的拓扑结构见图1.

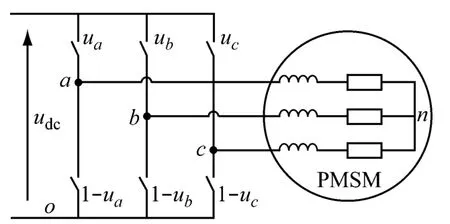
图1 三相电压型逆变器拓扑结构

图1 中，三相半桥电路控制三相电压(ua，ub，uc)的高低相位输出.每相半桥内两个开关通断相反(如ua和1－ua)，即仅有一个开关可以闭合，以避免半桥内部短路.同时，每相半桥电路可以输出高低两种电平，当上端开关闭合时输出高电平，反之为低电平.因此，单相半桥可能产生2种开关配置，三相半桥则有8(23)种开关配置.每种开关配置对应一组输出电压，见表1.

表1 逆变器开关配置与相间电压

当三组开关配置相同(即每相同时闭合上端或下端开关)时，逆变器无法形成电流回路，此时相间没有电压.这两组开关状态产生的矢量称为零矢量(U0与U7等价)，在后文中U0将不被应用于仿真模型.逆变器6组电压矢量和2组等价零矢量的分区和合成见图2.

图2 逆变器电压空间矢量的分区和合成

2 PMSM预测电流控制

PMSM预测电流控制的结构见图3，该闭环系统的主要控制变量为d，q轴电流.实时采集转速信号ω和三相定子电流ia，ib，ic，并通过坐标变换得到id，iq，与给定的参考电流 id0，iq0一起作为预测电流控制模块的输入.

图3 PMSM预测电流控制结构

PMSM预测电流控制遵循滚动优化思想，其原理是利用控制器内的动态模型，实时预测控制过程的未来趋势和变化.具体实施步骤如下.

步骤1 在采样时刻k，测量得到id(k)，iq(k)，ω(k)，并由7组电压矢量Ui(i=1，…，7)经坐标变换得到Ud(k)和Uq(k).

步骤2 利用 id(k)，iq(k)，Ud(k)，Uq(k)，ω(k)，根据式(9)得到7组预测电流 Id(k+1)，Iq(k+1).

步骤3 分别计算7组预测电流与参考电流id0，iq0的误差

步骤4 根据预测代价函数［15]

从7组预测电流矢量Ii(k+1)(i=1，…，7)中选取最逼近(即误差ei(i=1，…，7)最小)参考电流矢量I0的一组，作为采样时刻k+1的预测电流矢量.预测代价函数在线计算流程见图4.

图4 预测代价函数计算流程

步骤5 选择最优预测电流矢量Is(k+1)所对应的电压配置Ui(i=1，…，7)，决定图3中逆变器模块的开关状态，实现PMSM调速的预测电流控制.

步骤6 实时测出采样时刻k+1的电流id(k+1)和iq(k+1)，从k+1时刻开始重复使用上述步骤滚动优化.

3 PMSM调速系统仿真

3.1 PMSM调速仿真系统

采用MATLAB/Simulink仿真软件建立PMSM调速仿真系统，其主体结构见图5.

图5 PMSM调速仿真系统

参考电流id0，iq0和反馈电流id，iq被送入离散系统(Discrete System)模块，根据预测电流控制方法计算7组预测电流Ii(k+1)(i=1，…，7)，求出它们与参考电流的误差ei(i=1，…，7).将7组误差送入S函数编写的逻辑运算模块(Logic)中，求出最小误差后输出该组对应的电压矢量，通过直流电压模块(Udc)得到电机实际的三相电压，输入PMSM模型，其主要参数见表2.

表2 PMSM模型主要参数

3.2 预测电流控制仿真结果

在PMSM调速Simulink仿真系统中验证预测电流控制方法的性能.设定电机运行的初始转速为100π rad/s，在10 ms时引入10 000π rad/s2的加速度.为防止转速无限增加给系统带来危害，在40 ms时电机达到限制的最高转速400π rad/s，并持续30 ms.在70 ms时电机以－10 000π rad/s2的加速度开始减速，至90 ms时转速减至设定的200π rad/s后维持恒定.为更有效地观察PMSM调速系统的动态性能，除改变转速设定外还在仿真过程中加入负载变化.0～50 ms时电机空载运行，在50 ms时引入2.16 N·m的负载转矩.

仿真得到PMSM的电磁转矩曲线，见图6.10～40 ms时电机的加速转矩为1.8 N·m;50 ms时由于外部引入负载转矩，为维持转速恒定，电机的电磁转矩也升至2.16 N·m;70 ms时电机减速，电磁转矩相应减为0.36 N·m，以提供－1.8 N·m的减速转矩;90 ms时电机完成减速过程，电磁转矩恢复到2.16 N·m，以匹配外部负载，维持转速恒定.

图6 PMSM电磁转矩曲线

PMSM静止a-b-c坐标系三相定子电流曲线见图7.由图可知三相电流为相位相差120°的正弦纹波曲线.电流频率快速响应电机转速变化:随转速增大而变大、减小而变小.电流幅值快速响应电磁转矩变化:随转矩增大而变大、减小而变小.电流频率和幅值的快速响应均符合PMSM三相电流的控制规律.

图7 静止a-b-c坐标系三相定子电流曲线

PMSM旋转d-q坐标系两相电流曲线见图8.由图可知，d，q轴电流是以参考电流id0，iq0为基准的纹波曲线，随转速变化无较大波动，证明预测电流控制方法对电流控制的有效性.d轴电流一直在0附近振荡，在突加负载转矩时的瞬时振荡略增大.q轴电流与电机电磁转矩的变化趋势一致:在10～40 ms时保持在10 A;50～70 ms时保持在12 A;70～90 ms时保持在2 A;此后回升至12 A.

PMSM的转速曲线见图9.由图可见，预测电流控制方法可以使电机转速很好地跟随设定值，并且在增加负载转矩时仍能维持设定转速不变，证明该法对PMSM具有良好的调速特性.

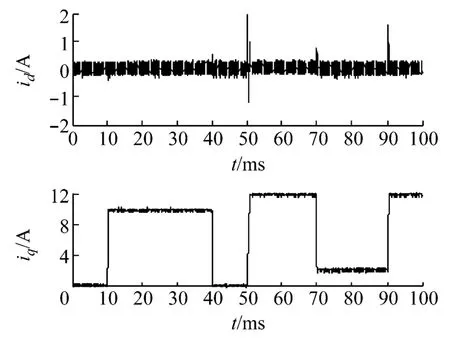
图8 旋转d-q坐标系两相电流曲线

图9 PMSM转速曲线

4 结论

在分析和建立 PMSM模型的基础上，利用MATLAB/Simulink实现PMSM的预测电流控制.仿真结果表明:波形符合理论要求，系统可以平稳运行，具有较好的动态性能.采用预测电流控制方法不仅可省去整定参数的复杂过程，而且可实时预测电流，具有一定优越性.通过仿真可有效地分析PMSM的特性，也可为实际电机控制提供可行策略和思路.

［1]杨建飞，胡育文.永磁同步电机最优直接转矩控制［J].中国电机工程学报，2011，31(27):109-115.

［2]邱鑫，黄文新，杨建飞，等.一种基于转矩角的永磁同步电机直接转矩控制［J].电工技术学报，2013，28(3):56-62.

［3]杨鸣，施伟锋.基于多种群遗传神经网络的船舶发电机故障诊断［J].上海海事大学学报，2013，34(4):18-22.

［4]周志斌，谢卫，LORON L.正弦永磁同步电机转矩脉动抑制［J].上海海事大学学报，2009，30(2):65-71.

［5]李耀华，郭巧娟，吴俊，等.永磁同步电机直接转矩控制系统开关表分析［J].电气传动，2012，42(11):15-17，22.

［6]李耀华，马建，刘晶郁，等.永磁同步电机直接转矩控制电压矢量选择区域［J].长安大学学报:自然科学版，2012，32(1):95-100.

［7]RODRIGUEZ J，PONTT J，SILVA C A，et al.Predictive current control of a voltage source inverter［J].IEEE Trans Ind Electron，2007，54(1):495-503.

［8]于蓉蓉，魏学业，吴小进，等.一种改进型预测电流控制算法［J].电工技术学报，2010，25(7):100-107.

［9]刘春海，梁晖.风力发电并网逆变器预测电流控制方法研究［J].电力电子技术，2010，44(10):6-8.

［10]年珩，於妮飒，曾嵘.不平衡电压下并网逆变器的预测电流控制技术［J].电网技术，2013，37(5):1223-1229.

［11]宋文祥，阮智勇，朱洪志，等.异步电机低开关频率的模型预测直接电流控制［J].上海大学学报:自然科学版，201319(6):647-653.

［12]LIU H，LI S.Speed control for PMSM servo system using predictive functional control and extended state observer［J].IEEE Trans Ind Electron，2012，59(2):1171-1183.

［13]MOREL F，LIN-SHI X，RETIF J M，et al.A comparative study of predictive current control schemes for a permanent magnet synchronous machine drive［J].IEEE Trans Ind Electron，2009，56(7):2715-2728.

［14]屈鲁，谢卫，卢颖娟，等.六相感应电动机调速系统的建模与仿真［J].上海海事大学学报，2012，33(2):94-99.

［15]MOON H T，KIM H S，YOUN M J.A discrete-time predictive current control for PMSM［J].IEEE Trans Power Electron，2003，18(1):464-472.