基于Petri网的海上事故应急流程绩效评价方法

尤庆华，杨伟伟，胡甚平，轩少永，陈莉

(上海海事大学商船学院，上海 201306)

0 引言

海上交通运输是现代交通运输的重要方式之一.据联合国有关部门统计，90%的世界贸易量是通过水路运输实现的.［1]然而海运业风险高，很容易发生海上交通事故，这给社会稳定和经济发展带来严重的影响.因此，分析研究海上交通事故应急系统的绩效，尽最大可能降低事故造成的损失，是保障海上交通运输安全及科学发展的基础性工作.1997年11月27日，国际海事组织(International Maritime Organization，IMO)通过A.852(20)号决议《船上紧急情况应急计划整体系统构成指南》，引导船舶应急计划趋于系统有序、实用高效，并为实施国际安全管理(International Safety Management，ISM)规则提供船岸一体化应急计划的编制指导.［2]ZHANG等［3]和HAO 等［4]对海上应急计划进行详细分析并建立以复杂层次结构和多个索引属性为特征的海上应急评价指标体系，并运用改进的模糊综合评价方法对海上应急计划以定性与定量相结合的方式进行全面评估，以提高安全水平和船舶交通效率.江建华［5]应用综合安全评估方法的原理和步骤评价船舶海上应急管理能力，并依据评价结果给出提高和改善船舶整体应急能力的建议.尚鸿雁［6]基于层次分析和模糊综合评价法建立危险货物运输应急能力评价指标体系和评价模型，并通过实证表明该模型有助于提高危险货物储运企业应急反应能力.汪爱娇［7]采用数据包络分析方法对海上应急基地运行效率进行评价，为相关管理单位采取措施提高应急服务的效率提供参考.同时，Petri网理论也被充分应用于各个学科的应急评价领域.宋宇博等［8]利用随机Petri网(Stochastic Petri Net，SPN)对城市轨道交通应急系统的安全性能进行分析，通过改变各状态的稳态概率提高系统的安全性能.刘韦光等［9]和张聪等［10]分别利用Petri网对消防应急救援指挥过程和井喷事故应急响应系统动态过程进行建模分析，为应急救援的有效指挥和优化提供理论依据.陈秋琳等［11]建立基于分层赋时Petri网的口岸通关流程模型并对该模型进行定量分析，应用Witness软件对所建模型进行仿真和口岸通关流程效率分析.上述尝试大多以系统建模为重心，并没有对模型进行充分的定量和定性分析.本文利用模糊SPN对海上事故应急系统进行建模，通过对所建的SPN模型进行静态分析和动态分析，获取海上事故应急流程的关键环节，以提高应急流程的有效性和合理性.

1 模糊SPN

Petri网理论诞生于20世纪80年代，因其在性能分析方面具有很大优势而得到较为广泛的应用.［12]模糊 SPN 为六元组(P，T，F，W，M1，λ－)，其中:P={P1，P2，P3，…，Pn}为有限的库所集，库所用“○”表示;T={t1，t2，t3，…，tm}为有限的变迁集，变迁用“□”表示;F⊆(P×T)∪(T×P)为存在于库所与变迁之间的流关系;W为弧权函数，W(P，T)和W(T，P)分别表示由库所到变迁和由变迁到库所的弧权;M1为库所的初始标识，以向量的形式表示，向量中第i个元素表示第i个库所中的托肯数目(取1表示库所获得一个托肯，取0表示没有托肯或失去托肯)，用 (记作Token)表示获得托肯的库所;是变迁引发率的模糊集，表示在可实施的情况下单位时间内平均实施次数的模糊数.

模糊SPN的基本思想是:对每一个变迁，从其被使能开始到引发的时间是一个连续的随机变量，一般认为这个时间间隔是服从指数分布的随机变量.用SPN对动态系统进行性能评价、分析和模拟，实质上是给出离散随机过程的一个图形化描述.［13]可以证明，SPN与连续时间马尔科夫链是同构的.为将SPN应用于流程的绩效评价，需要先建立系统SPN模型，再构造同构的马尔科夫链，最后基于马尔科夫链的稳态概率进行系统绩效评价.基于稳态概率可以进一步分析系统的绩效指标、繁忙程度以及整个系统的工作效率，并得到影响整个系统工作效率的主要因素，从而在后续工作中针对关键问题提出相应的解决办法.

2 海上事故应急流程SPN模型

船舶应急反应预案是为保证航运企业和海事执法机构对船舶突发事件能够迅速、有序并有效地开展应急与救援行动，减少人员伤亡，降低事故损失，而预先制定的救援计划和紧急行动方案.［14-15]本文参考海事执法部门制定的海上事故应急预案，考虑海上事故应急预案中的船舶监测预警装置、应急反应指挥部、应急反应营救工作小组之间的关系，分析应急流程的绩效.事故发生时，船舶监测预警装置迅速报警，并向应急反应指挥部传递相应的信息，应急反应指挥部根据事故类型及危害程度，与相对应的应急救助部门或机构取得联系并选择相应的应急措施，同时调派相应的应急救援组织实施救援.目前，海上交通事故可大致分为船体受损、人员伤亡、火灾爆炸和海洋污染等4类.当这类事故发生时，应急流程的分析、指挥以及救援派遣过程的SPN模型见图1.图1中各库所和变迁所代表的含义见表1.

图1 海上事故应急流程SPN模型

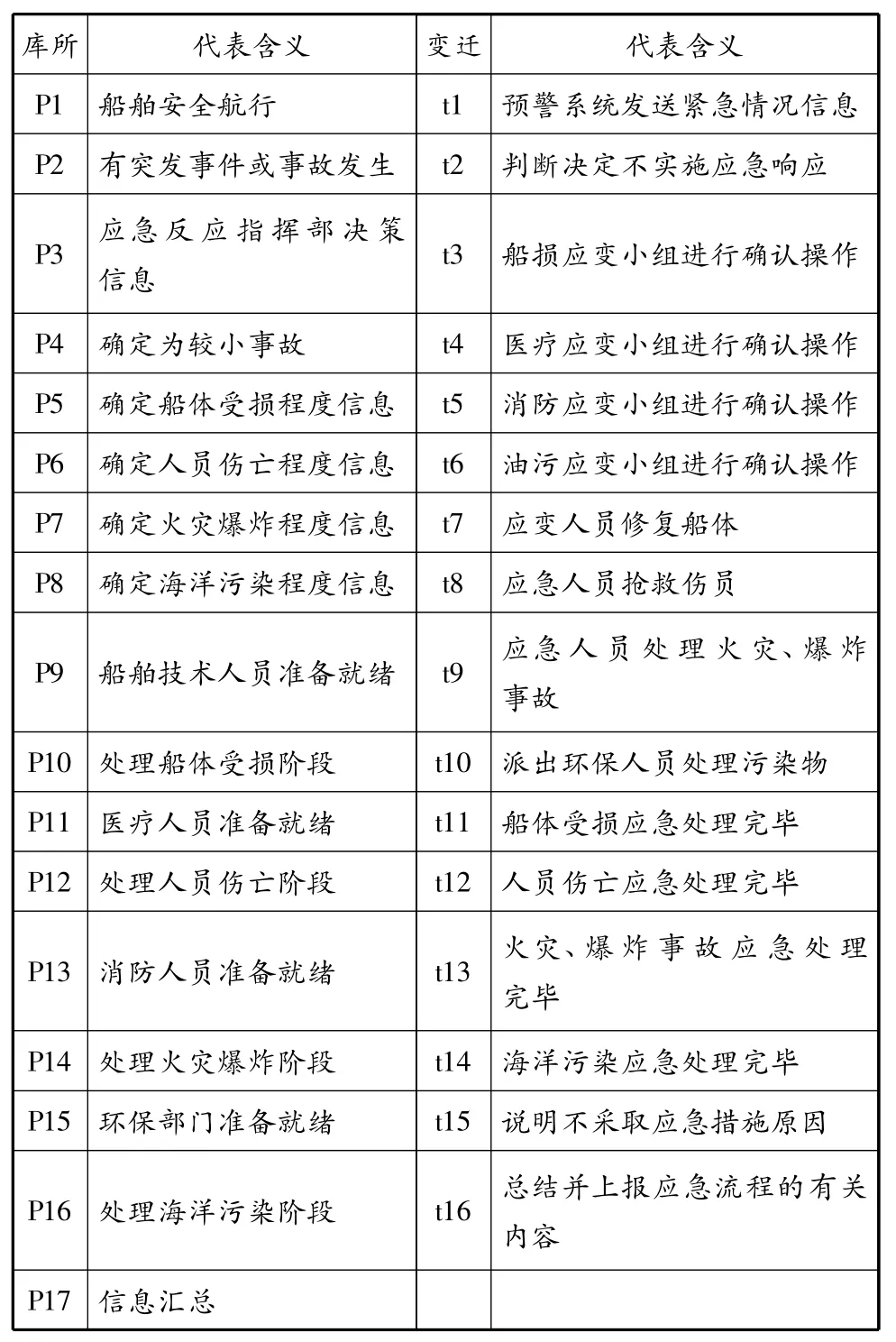
表1 各库所和变迁所代表的含义

如图1所示，当船舶在海上正常安全航行时，P1，P8，P10，P12，P14 中各有一个 Token，表示船舶预警系统工作正常，此时应急系统的SPN模型的初始标识为 M1=(1，1，0，0，0，0，0，0，1，0，1，0，1，0，1，0，0).本文主要目的是对船舶遇到事故时的应急流程的绩效进行分析.如图1，当有紧急情况或事故发生时，P2中也存在一个Token，可以将该标识记为M1(1，2，9，11，13，15).此时对应的情况如下:船舶有突发事件或事故发生，船舶报警系统进行报警，各类紧急救援组织准备就绪.根据前文提到的变迁触发规则，P1和P2中各有一个Token，使得变迁t1(即报警系统向应急反应指挥部发送的紧急情况信息)被使能并被触发后，库所P1失去一个Token并得到一个Token，另外一个Token触发库所P3，即应急反应指挥部接收报警信息.此时标识为 M2(1，3，9，11，13，15).

接着，变迁 t2，t3，t4，t5，t6 中任意一个都可以被库所P3中的Token所触发，此处5个变迁存在冲突，只能有一个变迁被触发，这需要根据事故实际情况进行合理判断.以t3被触发为例(即检测船体受损事故):t3被触发后，t3中的Token到达库所P5(表示已经确定船体受损程度信息)，标识变为M3(1，5，9，11，13，15)，此时库所 P9 中的 Token 已经准备就绪(即船舶技术人员准备就绪)，与库所P5一同触发t7(即技术人员修复船体，进行堵漏);t7的触发使得P10得到Token(表示进行船体修复、堵漏阶段)，此时标识为 M4(1，10，11，13，15);船体修复、堵漏工作完成后，变迁t11得到Token，并分配给库所P9和P17(即船舶技术人员重新进入备战状态并对应急流程的实施情况进行汇总)，此时标识为M5(1，9，11，13，15，17);P17 中的 Token 接着触发变迁t16(即总结并上报应急流程的有关内容).用类似的方法可以分析t2，t4，t5，t6被触发后的变化情况.

从所建的SPN模型可以得知:系统中没有一个变迁(任务)是孤立存在的，它们都有各自的输入输出库所，表明当船舶遇到紧急事故时任何救援任务都需要有一定的先行条件.Petri网中以冲突结构建立的t2，t3，t4，t5，t6这5个变迁需要根据实际事故情况进行判断选择，其他结构均是顺序结构，因此不存在死任务的情况，这说明救援过程中的各子任务都会发生，这是救援工作可以顺利完成的前提.由此可知，上图所建的SPN模型是合理、有效的.

3 算例

为分析上述SPN模型中的应急流程绩效，以某海域发生海上事故后执法部门实施的应急流程为例，通过查阅相关资料并结合数据挖掘方法和专家经验综合评价法［16]获取各个应急行动的实施效率等数据，结合以上模型进行绩效分析.

3.1 数据采集

模型中各个应急行动的实施时间为相互独立的随机变量，且服从指数分布，变迁t1，t2，…，t16的平均实施效率分别为 λ1，λ2，…，λ16，可以从应急流程的实施过程中统计得到.通过分析所采取的应急流程，得到λ1=10次/单位时，λ2=λ3=λ4=λ5=λ6=4次/单位时，λ7=λ8=λ9=λ10=3次/单位时，λ11=λ12= λ13= λ14=5 次/单位时，λ15= λ16=7次/单位时.受海上事故发生时各种因素的制约，所得到的各个变迁的实施效率的值不一定是精确数值.于是，在变迁的实施效率中引入表示不准确或不精确信息的模糊集.本文用三元组(a1，a2，a3)定义的三角形隶属函数表示模糊数，隶属函数为

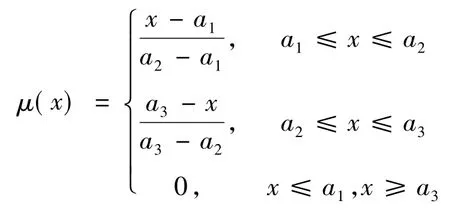
式中:参数 a2给出μ(x)的最大隶属度，即μ(a2)=1;参数 a1和a3给出模糊数据的最小和最大限.模糊数α截集定义为Aα={，，}，见图2.

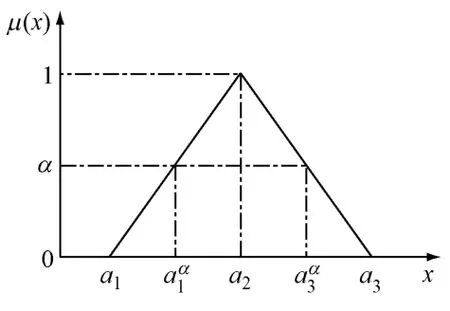
图2 三角形模糊数

对λ1的精确值采用±20%的模糊化程度作为其上下限，其余采用±10%的模糊化程度作为其上下限，则有:

取各个稳态概率的和为模糊数(0.9，1.0，1.1)，α 的范围为［0，1]，步长为，其中 i=1，2，…，12.

3.2 数据分析与推理

取得相应数据后，为对流程进行绩效分析，需给出与海上事故应急流程SPN模型同构的马尔科夫链.

由当前的状态标识 M1(1，2，9，11，13，15)出发，可以得到不同的触发变迁可达标识集:M1(1，2，9，11，13，15);M2(1，3，9，11，13，15);M3(1，5，9，11，13，15);M4(1，10，11，13，15);M5(1，9，11，13，15，17);M6(1，6，9，11，13，15);M7(1，9，12，13，15);M8(1，7，9，11，13，15);M9(1，9，11，14，15);M10(1，8，9，11，13，15);M11(1，9，11，13，16);M12(1，4，9，11，13，15).根据海上事故应急流程SPN 模型的 12 个状态 M1，M2，M3，…，M12，可得到与其同构的马尔科夫链.图3中的有向弧表示应急过程中的SPN模型从一个状态到另一个状态的转换.

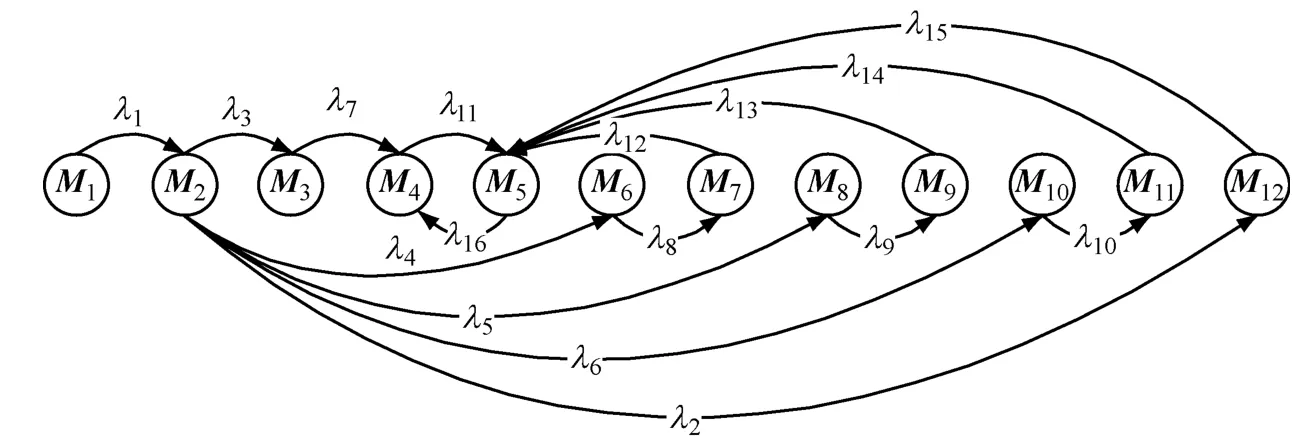
图3 与SPN同构的马尔科夫链

设p(Mi)为海上事故应急流程SPN模型处于状态Mi的概率，可以得到如下式所示的状态概率间的关系式:

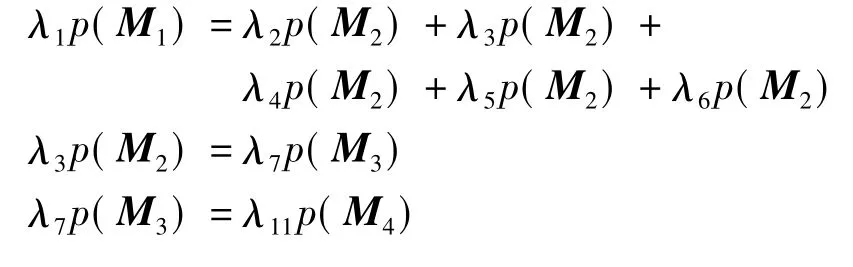
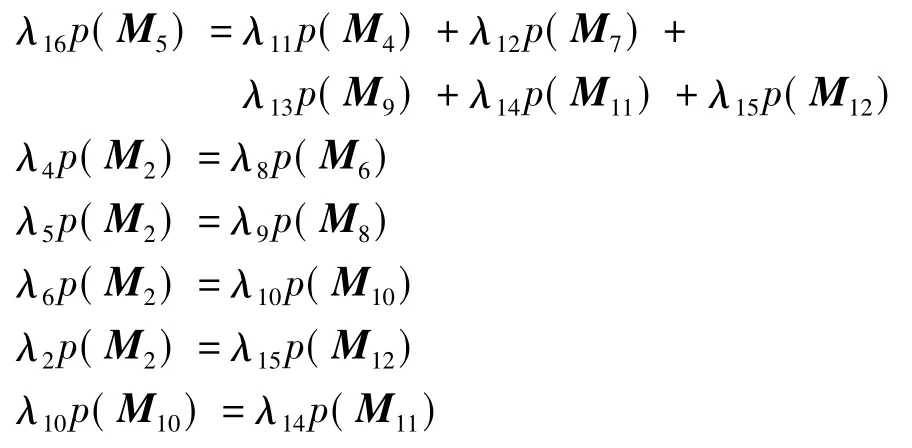
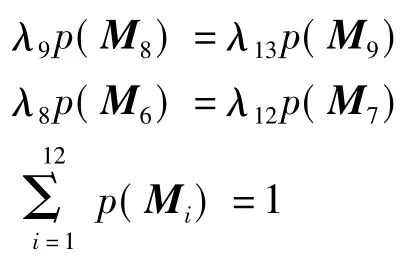
求解方程组可以计算出各状态的稳态概率:

利用区域中心法对上述矩阵进行解模糊，可得各状态的稳态概率:p(M1)=0.135 2;p(M2)=0.066 7;p(M3)=p(M6)=p(M8)=p(M10)=0.089 0;p(M4)=p(M7)=p(M9)=p(M11)=0.053 4;p(M5)=0.190 6;p(M12)=0.038 1.

通过以上各稳态概率，可以计算出船舶在遇到紧急情况时各库所的繁忙度以及各变迁的利用率.各库所的繁忙度:p{T2=1}=p(M1)=0.135 2;p{T3=1}=p(M2)=0.066 7;p{T4=1}=p(M12)=0.038 1;p{T5=1}=p{T6=1}=p{T7=1}=p{T8=1}=p(M3)=0.089 0;p{T10=1}=p{T12=1}=p{T14=1}=p{T16=1}=p(M4)=0.053 4;p{T17=1}=p(M5)=0.190 6.其中，Ti为各库所中的Token数目.

各变迁的利用率:U(t1)=0.135 2;U(t2)=U(t3)=U(t4)=U(t5)=U(t6)=0.066 7;U(t7)=U(t8)=U(t9)=U(t10)=0.089 0;U(t11)=U(t12)=U(t13)=U(t14)=0.053 4;U(t15)=0.038 1;U(t16)=0.190 6.

从以上数据可以得出，库所 P9，P11，P13，P15的繁忙度值较大，船舶事故发生时可以把各个应急部门的准备时间和精力往其他应急环节倾斜.除此之外，库所P17繁忙度值也较大，表示应急完成后对应急信息汇总的繁忙程度较高，因此需要各个应急部门一起协作完成这项工作.从以上数据还可以得出，变迁t1和t16的利用率较大，表示报警系统进行报警的概率和总结应急流程实施情况的概率比较大，船舶安全部门应该加强对报警装置的监控，船员和其他相关人员切不可玩忽职守.

通过对以上各个因素的静态分析，可以根据各个状态稳态概率的值得出各个应急环节对船舶应急绩效的影响.除此之外，应急部门也可以根据自己救援的需要和应急的实际情况，对某单因素进行动态分析，以体现应急系统各因素之间的关系，并通过数值变化趋势反映不同状况下海上事故应急流程的关键所在.下面以 λ1，λ2，λ3，λ7为例进行动态分析.

假定 λi(i=2，…，16)的值分别为 λ2=4，λ3=6，λ4=3，λ5=5，λ6=5，λ7=7，λ8=5，λ9=4，λ10=7，λ11=3，λ12=3，λ13=2，λ14=4，λ15=6，λ16=7.通过改变λ1的值求解上述状态转移方程，得到p(Mi)(i=1，…，12)随着λ1的变化而变化的情况，见图4.

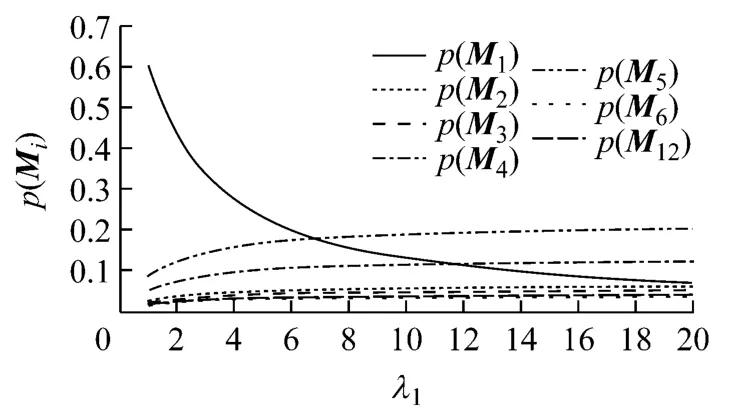
图4 改变λ1时系统各状态的稳态概率

从图4可以看出:随着λ1的增大(即船舶报警系统报警情况增多)，p(M1)迅速降低(即船舶正常航行的概率大幅降低).同时 p(M2)，p(M3)，p(M4)，p(M5)，p(M6)的值都有所增加，表示船舶处于紧急事故状态，需要各应急部门采取行动的概率也有所增加.同时p(M5)的值也显著增加，表示当报警系统经常发送紧急情况时，总结和汇总信息的概率也随之增加.

同样，当设定λ1=5，改变λ2的值时，各状态的稳态概率见图5.

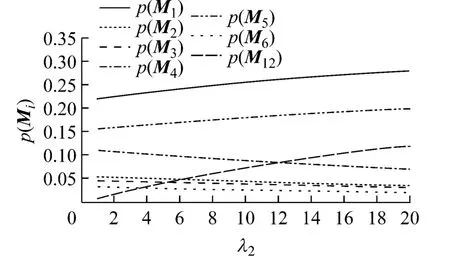
图5 改变λ2时系统各状态的稳态概率

从图5可以看出:λ2增大(即船长和船公司决定不实施应急流程的频率增加)时，p(M1)和p(M5)均有所增加，即船舶有不需要实施应急流程的情况或小事故发生，同时需要总结和汇总信息的概率也随之增加;p(M12)的值迅速增加，表示被确定为较小事故的可能性迅速增加;p(M2)，p(M3)，p(M4)，p(M6)随着λ2增大均有所降低，表示需实施应对船舶受损等应急行动的概率降低.

当改变λ3的值时，各状态的稳态概率见图6.

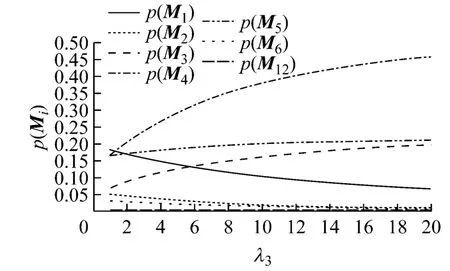
图6 改变λ3时系统各状态的稳态概率

从图6可以看出:随着λ3(船体受损的概率)的不断增大，p(M3)和p(M4)的值也迅速增大，表示需要检测船体受损程度及进行船体修复、堵漏阶段的概率迅速增大.

当改变λ7的值时，各状态的稳态概率见图7.

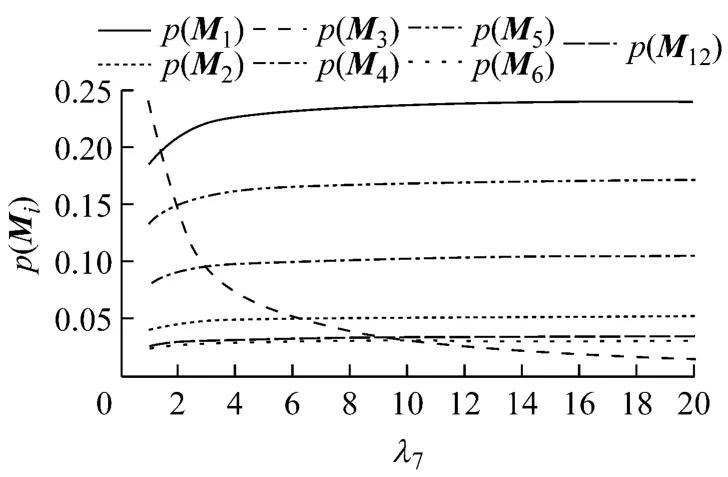
图7 改变λ7时系统各状态的稳态概率

从图7可以看出:随着λ7(派出技术人员修复船体的频率)的不断增大，p(M3)迅速降低，表示船体受损的概率大幅降低.λ7的改变对其他稳态概率影响不大，只对p(M3)影响较大.

4 结论

利用模糊SPN对海上交通事故应急系统的绩效进行静态和动态分析，通过静态分析对当前各个应急行动的实施效果进行评价，找出应急过程中需要加强的环节以提高应急处置能力.通过静态分析可以得出:该执法机构在船舶事故应急处理时应该把重心放在事故处理环节，以达到资源配置的平衡.同时船舶安全监测部门应该重视对报警装置的监控，船员和其他相关人员在值班时应严密监视船舶报警装置，在事故发生的第一时间采取应急措施，以最大限度降低事故损失.通过动态分析可知:应急系统中各个因素都会对整个应急流程的实施效率产生影响，提高某个变迁的实施速率对提高应急系统的可行性和有效性有相当大的作用.通过各方面的协调和对应急处理现场实际情况的改进，可以争取在有限的时间里更有效地进行营救操作.

海上交通事故应急流程绩效评价是一个比较新颖的研究课题，本文仅初步给出海上事故应急流程的简单模型及分析方法，在后续的研究中可以建立更合理的模型并进行深入分析.

［1]姚杰，任玉清，李玉伟.基于事故树分析的海上交通事故的研究［J].大连海洋大学学报，2010，25(4):348-352.

［2]IMO A852(20).船上紧急情况应急计划整体系统构成指南［S].MSC，IMO，1997.

［3]ZHANG Hao，XIAO Yingjie，YU Bin，et al.Comprehensive evaluation of maritime emergency capability［C]//2nd Int Conf Comput＆ Network Technol(ICCNT).Bangkok，Thailand，2010:452-456

［4]HAO Yong，JIANG Changyun，TAN Qinwen.Capability evaluation of maritime emergency management system［C]//Distributed Computing＆ Applications to Business，Eng＆ Sci(DCABES)，2012 11th Int Symposium，2012:348-352.

［5]江建华.船舶海上应急评价初探［J].中国安全生产科学技术，2012(1):187-192.

［6]尚鸿雁.基于AHP-F的危险货物运输应急能力评价模型［J].上海海事大学学报，2008，29(4):21-24.

［7]汪爱娇.基于偏好DEA的海上应急基地运行效率评价［J].中国安全科学学报，2011(5):126-131.

［8]宋宇博，牟海波，蒋兆远.基于随机Petri网的城市轨道交通应急系统安全性能分析［J].中国安全科学学报，2011(9):82-87.

［9]刘韦光，赵培，赵云胜.基于Petri网的消防应急救援指挥过程建模与性能优化［J].安全与环境工程，2012(3):88-92.

［10]张聪，李辉，何华刚.基于Petri网的井喷事故应急响应系统动态过程建模［J].安全与环境工程，2013(3):82-85，90.

［11]陈秋琳，杨勇生，孟燕萍，等.基于HTPN的口岸通关流程效率分析［J].上海海事大学学报，2009，30(3):5-8.

［12]林闯.随机Petri网和系统性能评价［M].北京:清华大学出版社，2005:146-202.

［13]原菊梅，侯朝桢，王小艺，等.基于随机Petri网的可修系统可用性模糊评价［J].计算机工程，2007(8):17-19.

［14]李珊珊，郑中义.基于Petri网的船舶碰撞事故致因［J].大连海事大学学报，2010，36(4):5-7，20.

［15]艾厚文，贾利民，秦勇.基于随机Petri网的铁路应急救援流程化分析［J].铁路计算机应用，2008(7):9-11.

［16]黄晓霞，程论.综合评价与数据挖掘的比较［J].上海海事大学学报，2007，28(4):54-58.