基于多新息理论的PID神经网络改进算法

孙敏敏 秦品乐

（中北大学计算机与控制工程学院 山西 030051）

0 引言

文[1]将PID控制与神经网络结合，提出了PID神经网络，PID神经网络具有PID控制规律，与传统的前向神经网络相比具有神经元的输入输出呈现出动态性，原因在于往神经网络中引入了比例（P）、积分（I）、微分（D）神经元。PID神经网络同时具备传统前向神经网络逼近任意非线性函数的特性，能够进行非线性，动态复杂系统的辨识与控制。文[2]采用BP算法的批处理模式进行神经元网络权值的调整，不便于系统实时辨识和控制，受文[3]的启发，采用BP算法的在线模式进行权重值的修正进行系统辨识，这为本文将多新息辨识算法引入PID神经网络做了准备。PID神经网络采用传统的BP算法的批处理模式进行权值的修正，从辨识的精度上考虑，批处理法拟合系统实际输入输出的效果优于在线模式，但从实时辨识与控制角度考虑，在线模式优于批处理法。在线模式对权值的修正值利用了系统当前的输入输出数据，没有利用历史的输入输出数据，坏数据对网络权值修正的影响大。丁锋等人提出的多新息辨识方法利用当前与历史输入输出数据，能减小坏数据的影响，提高系统辨识的精度。受文[4]启发，本文将多新息辨识方法引入PID神经网络，提出基于PID神经网络的多新息学习算法并给出了收敛性证明，仿真实例说明能取得较好的效果。

1 PID神经网络多新息学习算法

考虑1+−pt到t时刻的p组输入输出数据，PID神经网络输入层各节点的输出向量为

输出层节点的输出向量为

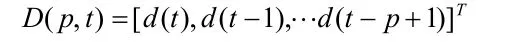
理想输出向量为

误差函数变为

那么，PID神经网络的隐含层至输出层权值修改式为

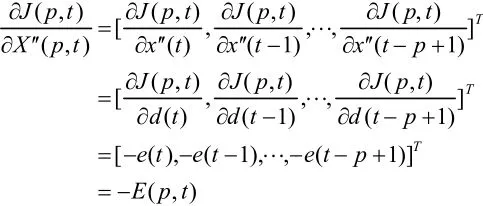
网络的输入层至隐含层权值修改式为

从而有隐含层至输出层权值修改式为

输出层至隐含层权值调整式为

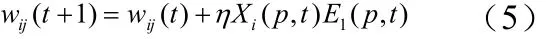
2 仿真实例

为了说明所提出的基于PID神经网络的多新息学习算法的有效性，在和PID神经网络采用的标准BP算法进行比较时，采用文献[7]中的例子。

例1.考虑下面方程描述的非线性动态系统

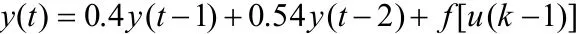
其中)(ty为t时刻系统输出，)(tu为t时刻系统输入。

输入函数为

网络采用在线梯度法，每个学习回合采集200个样本点进行学习和训练，输入层至隐含层权值矩阵的初始值为W(0)=[1,0.1,1;−1,−0.1,−1]，隐含层至输出层权值向量的初始值为V(0)=(0.1,0.1,0.1)，其中y(t)为网络理想输出，d(t)为网络实际输出。取新息长度p=2，学习率η=0.175，当网络学习和训练20步后，改进算法与未改进算法的辨识结果如图1和图2所示。

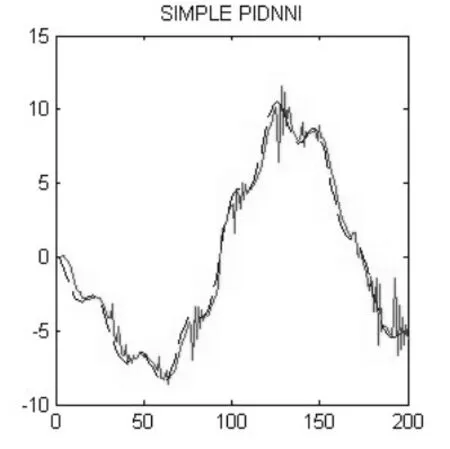
图1 未改进算法的辨识结果

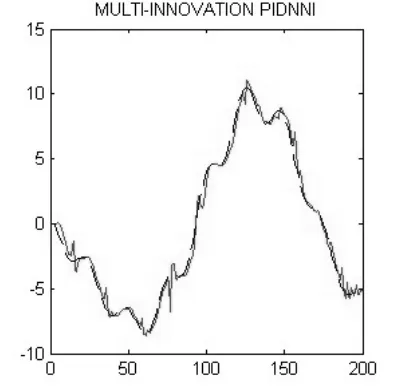
图2 改进算法的辨识结果

3 结语

结合多新息辨识理论，推导出基于多新息理论的PID神经网络算法。仿真实例表明所提出的算法能有效估计参数，且具有较快的收敛速度。

[1]舒怀林.PID控制与神经网络的结合及PID神经网络非线性控制系统[M].第十九届中国控制会议论文集（二），2000：228-332

[2]舒怀林.PID神经元网络及其控制系统[M].北京：国防工业出版社，2006：23-51

[3]许少云.BP学习算法的在线模式与批处理模式[M].1996年中国智能自动化学术会议论文（上册），1996

[4]刘英玉.一种基于前向神经网络的多新息随机梯度算法[J].哈尔滨商业大学学报（自然科学版）2006，22（2）

[5]Feng Ding，Tongwen Chen.Performance analysis of multi-innovation gradient type identification methods.2009，43（1）：1-14

[6]郭雷.时变随机系统-稳定性、估计与控制.长春：吉林科学技术出版社，1993

[7]舒怀林.PID神经网络及其非线性动态系统辨识能力分析[J].自动化与信息工程