改进的单纯形法迭代计算方法

吴庆丰

淮北师范大学数学科学学院，安徽淮北 235000

改进的单纯形法迭代计算方法

吴庆丰

淮北师范大学数学科学学院，安徽淮北 235000

1 引言

单纯形法是求解线性规划的基本方法，许多文献对其不断改进。若求解线性规划问题时，存在基可行解或对偶问题的基可行解，则可直接采用文献[1]的方法。文献[2]给出了一种新的原对偶单纯形法，文献[3-4]提出了一种push-to-pull的单纯形算法，文献[5]提出了一种求解线性规划的新单纯形类算法，并与H.Arsham提出的push-to-pull算法作了比较，文献[6]提出了一种修正的二分单纯形法，文献[7-8]给出了求解线性规划的摄动单纯形法，文献[9]提出了基于矩阵初等变换初始可行基的获得方法，得到基于单纯形法的求解线性规划模型的直接方法。文献[9]的方法其实是对初始系数矩阵进行初等行变换得到一个单位子矩阵，给出了一种新的得到初始可行基的思路，但此法主要是在进行人工计算时可一定程度简化计算，不便于将算法在计算机上实现，而且在计算机上编程实现该算法也很难降低计算量。如果算法能与计算机结合起来，便于在计算机上实现，那么将更利于实际应用，特别是较大规模的线性规划问题求解更需要借助于计算机。本文给出的算法既考虑到利用人工计算求解线性规划能够简化计算降低计算量，更重要的是又考虑算法与计算机相结合。

设有线性规划问题：

其中c∈Rn，x∈Rn，A∈Rm×n，b∈Rm，b≥0，这里向量均为列向量。将系数矩阵A按列分块，A=(p1，p2，…，pn)，设B是可行基，cB为基B对应的目标系数，检验数σj=cj-cTBB-1pj，j=1，2，…，n。

单纯形法的基本思想是从一个基可行解向相邻的另一个改进的基可行解迭代，当所有检验数σj≤0时，线性规划问题达到最优解。

单纯形法计算中的几个问题：

（1）目标函数极小化时解的最优性判别。这时只需以所有检验数σj≥0作为判别表中解是否最优的标志。

（2）退化。按最小比值来确定换出基的变量时，有时出现存在两个以上相同的最小比值，从而使下一个表的基可行解中出现一个或多个基变量等于零的退化解。退化解的出现原因是模型中存在多余的约束，使多个基可行解对应同一顶点。当存在退化解时，就有可能出现迭代计算的循环，尽管可能性极其微小。为避免出现计算的循环，1974年勃兰特（Bland）提出了一个简便有效的规则：（1）当存在多个σj＞0时，始终选取下标值为最小的变量作为换入变量；（2）当计算θ值出现两个以上相同的最小比值时，始终选取下标值为最小的变量作为换出变量。

（3）无可行解的判别。当线性规划问题中添加人工变量后，无论用人工变量法或两阶段法，当求解结果出现所有σj≤0时，如基变量中仍含有非零的人工变量（两阶段法求解时第一阶段目标函数值不等于零），表明问题无可行解。

2 大M法

若化为标准形后的线性规划问题中约束条件的系数矩阵中不存在单位矩阵，引入人工变量。下面通过举例说明大M法求解线性规划以便于与改进的大M法进行比较。

例1用单纯形法求解线性规划问题

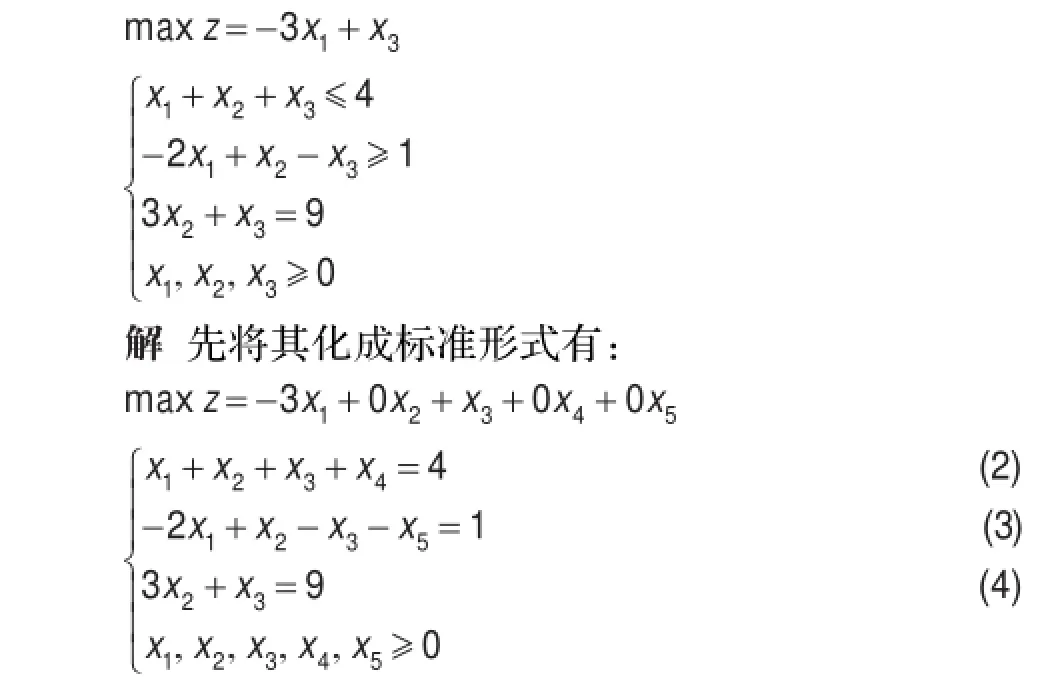
这种情况下，可以通过添加两列单位向量p6，p7，使连同约束条件中的向量p4构成单位矩阵：

p6，p7是人为添加上去的，它相当于在上述问题的约束条件式（3）中添加变量x6，约束条件式（4）中添加变量x7，变量x6，x7相应称为人工变量。由于约束条件式（3）、式（4）在添加人工变量前已是等式，为使这些等式得到满足，在最优解中人工变量取值必须为零。为此，令目标函数中人工变量的系数为任意大的负值，用“-M”代表。“-M”称为“罚因子”，即只要人工变量取值大于零，目标函数就不可能实现最优。因而添加人工变量后，例1的数学模型形式就变成为：

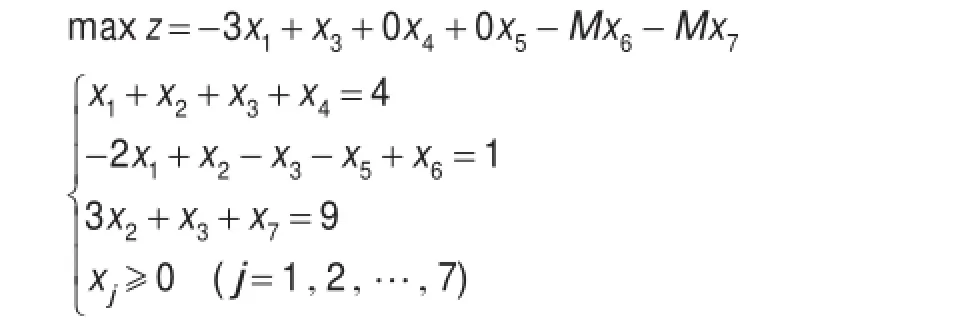
该模型中与p4，p6，p7对应的变量x4，x6，x7为基变量，令非基变量x1，x2，x3，x5等于零，即得到初始基可行解x(0)=(0，0，0，4，0，1，9)T，并列出初始单纯形表，在单纯形法迭代运算中，M可当作一个数学符号一起参加运算。检验数中含M符号的；当M的系数为正时，该检验数为正，当M的系数为负时，该项检验数为负。例1添加人工变量后，用单纯形法求解的过程见表1。

表1 大M法迭代过程

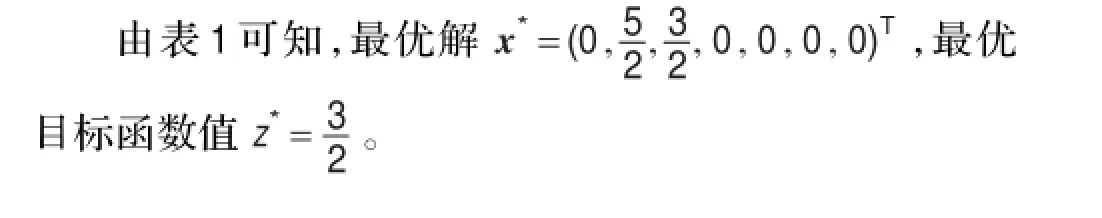
3 改进的大M法

当计算检验数表达式中含有M时，结果为（系数×M±常数），因为M很大，很明显，其值的符号和大小由M的系数符号和大小决定，所以在计算时，只需计算含有M的部分的值即可。这样可以降低一些运算量。另外，在单纯形法迭代过程中，当人工变量全部由基变量变成非基变量时，可以在单纯形表中将人工变量部分的表格去掉，然后继续进行计算，这样可以再次降低运算量。

为了方便下文叙述，这里将上述方法计算含有M表达式的检验数称为有效检验数。有效检验数：当计算检验数表达式含有M时，只计算含有M的表达式的值；当不含M时，按照原公式计算。

下面给出改进的大M法的计算步骤：

第1步添加人工变量得初始基可行解，列出初始单纯形表。

第2步最优性检验。

计算有效检验数。如表中所有有效检验数σj≤0，当基变量中含有非零的人工变量时，则问题无可行解，基变量中不含有人工变量时，表中的基可行解即为最优解（此时，当某非基变量有效检验数为零时，问题有无穷多最优解，否则有唯一最优解），计算结束。当表中存在σj＞0时，如有pj≤0，则问题为无界解，计算结束；否则转下一步。

第3步检验是否去掉人工变量。当表中人工变量有效检验数σj≤0时，人工变量由基变量变为非基变量，此时去掉含有人工变量部分的表格，转下一步。

第4步从一个基可行解转换到相邻的目标函数值更大的基可行解，列出新的单纯形表。

（1）确定换入基的变量。只要有检验数σj＞0，对应的变量xj就可作为换入基的变量，当有一个以上检验数大于零时，一般从中找出最大一个σk。

σk=max{σj|σj＞0}

其对应的变量xk，作为换入基的变量（简称换入变量）。（2）确定换出基的变量。由下式确定θ：

确定xl，是换出基的变量（简称换出变量）。元素alk决定了从一个基可行解到相邻基可行解的转移去向，取名主元素。

（3）用换入变量xk替换基变量中的换出变量xl，得到一个新的基(p1，…，pl-1，pk，pl+1，…，pm)。对应这个基可以找出一个新的基可行解，并相应地可以画出一个新的单纯形表。

第5步重复第2～4步，一直到计算结束为止。

这里采用改进的大M法求解例1，求解过程见表2。

表2 改进的大M法迭代过程

计算结果同表1，但比较表1和表2的计算过程不难发现，表2在计算检验数时，如果结果含有M则不必计算含M的表达式所加减的那些常数，这样使得计算过程简化，而且表2迭代计算到第二次时，人工变量已经由基变量变为非基变量，此时基可行解中人工变量取0，此后计算过程直接去掉了人工变量部分的表格，从而再次降低计算量。

4 改进的大M法与两阶段法相结合的算法

实际上，当检验数表达式中含有M时，只需计算M的系数即可，从而再次简化运算，当存在M的系数为正时，只考虑M的正系数部分来确定换入基的变量，取最大的正系数对应的决策变量作为入基变量。出基变量的选择与原来相同。当然此法更重要的是利用计算机求解时可以克服M的选取与aij，bi或cj的参数值之间的不良影响所导致的计算结果错误。下面的方法无需给出M。

设式（1）为标准化的线性规划问题，添加人工变量得到初始单位基矩阵，将式（1）化为如下线性规划问题。

这里x=(x1，…，xn，xn+1，…，xn+m)T，e=(1，1，…，1)T∈Rm。

计算检验数时，若表达式含有某些人工变量的目标系数cn+1，cn+2，…，cn+m，记为1，2，…，r，r≤m，显然1，2，…，r的值均为-1，则检验数为：

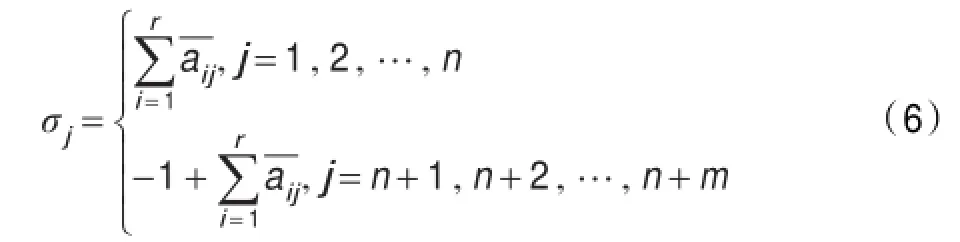
此算法的详细步骤跟改进的大M类似，只是目标函数不含M，计算检验数时有一点差别，这里不再赘述。

5 收敛性分析

单纯形方法是求解线性规划问题的出现较早的一个算法，在理论和实践上都比较完善，但它不是多项式时间算法。在采用Bland’s法则进行转轴操作（相同值的情况下取字典序最小）之后，可以证明单纯形法一定能够在有限步之后终止[10-11]，但是最坏情况算法的时间复杂度为指数级别的，而且可以构造出让单纯形法的时间复杂度达到指数级别的具体实例。不过实践证明在绝大多数情况下单纯形法的效率非常令人满意。单纯形法的最坏时间复杂度为指数级别，并不意味着线性规划不存在多项式级别的算法。椭球算法和内点算法均为解决线性规划的多项式时间算法。虽然Khachigan和Karmarkar分别在1979年和1984年提出了求解线性规划问题的多项式时间算法。但就计算工作量而言，一般情况下都没有单纯形方法好。从大量数值计算结果分析，K-变形算法优于Karmarkar算法，从同一内点出发达到同样精度要求的解所需迭代次数，K-变形方法要优于Karmarkar方法，而对多数问题来说，单纯形法又优于K-变形方法和Karmarkar方法，但也有一些情况下单纯形法不如Karmarkar方法和K-变形方法。通过大量的计算表明，对于多数问题来说，单纯形法要明显地优于Karmarkar算法及其变形算法[12]。

本文算法主要改进有：

（1）计算检验数时，只计算有效部分使得计算简化。

（2）迭代到适当步骤，去掉人工变量，减小计算规模，降低计算量，减少存贮空间。

（3）解决利用计算机求解时由于大M值的影响所可能导致的错误。

本文给出的算法不会减少迭代次数，但会降低计算量及计算机存贮空间，由于不改变迭代次数，从任一基可行解开始，采用Bland’s法则进行转轴操作一定能够在有限步之后终止。要减少迭代次数，需要改变枢轴元素选取准则。文献[13]提出一种新的入基准则为最大加权检验数准则，并利用随机模拟方法将该入基准则与其他入基准则进行比较，结果表明该准则优于最大检验数准则和最大上升准则。文献[14]给出了一种新的选择入基变量的准则，减少了单纯形法的迭代次数。文献[15]给出了一个新的迭代进出基准则即最大增量准则，可以加快迭代速度，同时也可以避免迭代中可能遇到的所谓循环。但文献[16]通过大规模的数值实验结果表明，文献[15]这种改进的单纯形算法虽然在大部分问题上的迭代次数比经典的单纯形算法有所减少，但所耗费的计算时间却普遍增加，其计算效率随着问题规模的增大而不断下降。文献[17]给出了单纯形法中确定主元素的两个新法则，即按使目标函数值增加得最多的原则确定主元素和按使目标函数值增加得最快的原则确定主元素，具有迭代次数更少、收敛速度更快的特点。本文所给出的算法也可以采用如文献[13-14，17]等所提供的新的枢轴主元的选取方法，迭代次数相应会有所降低。

6 结束语

用大M法处理人工变量，在用手工计算求解时不会碰到麻烦。但用电子计算机求解时，对M就只能在计算机内输入一个机器最大字长的数字。如果线性规划问题中的aij，bi或cj等参数值与这个代表M的数相对比较接近，或远远小于这个数字，由于计算机计算时取值上的误差，有可能使计算结果发生错误。为了克服这个困难，通常可以对添加人工变量后的线性规划问题分两个阶段来计算，称两阶段法。而两阶段法需要将目标函数分为两个阶段，破坏了目标函数的一致性。这里也可以采用本文给出的两种改进的方法，可以避免由计算机求解时由于M的选取与aij，bi或cj的参数值以及计算机计算误差所产生的不良影响。并当人工变量全部由基变量变成非基变量时，可以在单纯形表中将人工变量部分的表格去掉，这样相当于又结合了两阶段法的优点。实际上，人工变量的出现只是为了方便得到初始单位基矩阵，在计算过程中，如果到某一步人工变量全部由基变量变成非基变量而此时仍需继续迭代计算时，由于基可行解中非基变量取0，所以此时完全没有必要继续带着人工变量进行计算。

[1]程理民，吴江，张玉林.运筹学模型与方法教程[M].北京：清华大学出版社，2007.

[2]燕子宗，费浦生，万仲平.线性规划的单纯形法及其发展[J].计算数学，2007，29（1）：1-14.

[3]Arsham H.An algorithm for simplex tableau reduction：the push-to-pull solution strategy[J].Applied Mathematics and Computation，2003，137（2）：525-547.

[4]Arsham H，Baloh P，Damij T，et al.An algorithm for simplex tableau reduction with numerical comparison[J].International Journal of Pure and Applied Mathematics，2003，4（1）：53-80.

[5]李炜.一个新的单纯形类算法[J].数学理论与应用，2003，23（3）：118-122.

[6]Pan P Q.A modified bisection simplex method for linear programming[J].Journal of Computational Mathematics，1996，14（3）：249-255.

[7]Pan Pingqi.A new perturbation simplex algorithm for linear programming[J].Journal of Computational Mathematics，1999，17（3）：233-242.

[8]Pan Pingqi.Primal perturbation simplex algorithms for linear programming[J].Journal of Computational Mathematics，2000，18（6）：587-596.

[9]申卯兴，许进.求解线性规划的单纯形法的直接方法[J].计算机工程与应用，2007，43（30）：94-96.

[10]Bland，Robert G.New finite pivoting rules for the simplex method[J].Mathematics of Operations Research，1977，2（2）：103-107.

[11]周勤学，丘兆福.Bland避免循环的单纯形方法的改进[J].中山大学学报：自然科学版，1989，28（3）：113-115.

[12]王晓慧，邢丽君.单纯形法与Karmarkar算法及其变形算法的比较[J].东北电力学院学报，1997，17（1）：28-33.

[13]林福荣，陈东宜.单纯形法的一种新的入基准则[J].曲阜师范大学学报：自然科学版，2002，28（4）：25-28.

[14]申卯兴，叶微，刘毅，等.单纯形法中枢轴元素选取准则的改进[J].计算机工程与应用，2003，39（25）：57-58.

[15]王全文，吴育华，吴振奎，等.单纯形法选择进出基变元的一个新准则[J].数学的实践与认识，2009，39（14）：75-81.

[16]高培旺.关于“单纯形法选择进出基变元的一个新准则”的计算效率[J].河南工程学院学报：自然科学版，2012，24（2）：61-64.

[17]罗进，张志军，刘任河.单纯形法中确定主元素的两个新法则[J].武汉工程大学学报，2008，30（1）：122-124.

WU Qingfeng

School of Mathematical Sciences,Huaibei Normal University,Huaibei,Anhui 235000,China

Improved big-Mmethod is presented.If expressions of the calculated test number containM,the only portion containingMis calculated,and thereby the calculation is simplified.And when artificial variables become nonbasic variables by basic variables in the iterative calculation process,the artificial variables parts of the table can be directly removed and then the calculation is continued.Thus,the amount of computation is again reduced.Taking advantages of two-phase method,an iteration algorithm without giving the bigMis further given.This method does not undermine the consistency of the objective function,and the calculation error can be avoided when using traditional big-Mmethod combined with computer to solve,due to the improper selection of the value ofM.

linear programming;simplex method;big-Mmethod;two-phase method

对传统大M法进行改进，若计算检验数的表达式中含有M则只计算含有M的部分，从而简化计算，迭代过程中当人工变量由基变量变为非基变量时，直接去掉人工变量部分的表格然后继续计算，从而再一次降低计算量。借鉴两阶段法的优点进一步给出了无需给出大M的迭代算法，此法不会破坏目标函数的一致性，而且可以避免传统大M法在利用计算机求解时由于M值的选取不当所导致的计算错误。

线性规划；单纯形法；大M法；两阶段法

A

O22

10.3778/j.issn.1002-8331.1210-0107

WU Qingfeng.Improved iterative calculation methods of simplex algorithm.Computer Engineering and Applications, 2014,50（18）：59-62.

安徽省高等学校省级自然科学研究项目（No.KJ2011B152）。

吴庆丰（1979—），男，讲师，研究领域：最优化理论及算法。E-mail：wuqingfeng6@163.com

2012-10-12

2013-01-18

1002-8331（2014）18-0059-04

CNKI网络优先出版：2013-02-07，http://www.cnki.net/kcms/detail/11.2127.TP.20130207.1420.015.html