离散晶格的正族、负族及其Hamilton结构
常辉,屈哲,陶可勤
(青岛滨海学院数学教研室,山东青岛266555)
离散晶格的正族、负族及其Hamilton结构
常辉,屈哲,陶可勤
(青岛滨海学院数学教研室,山东青岛266555)
构造了一个新的等谱问题,利用相容性条件,推导出离散晶格方程的正族和负族.再利用迹恒等式,建立其Hamilton结构.获得的离散方程族的达布变换、双线性化、对称、守恒率及其精确解也值得进一步研究.
晶格方程;正族;负族;迹恒等式;Hamilton结构
1 引言
许多物理、化学、生物现象都可以用离散晶格方程或连续的时间演化方程来描述,如: Toda晶格方程、离散或连续的KdV方程等.近年来,连续或离散可积方程族的研究引起研究人员极大的关注[1-5].寻找非线性可积方程族并研究其双线性化、恒率、Hamilton结构及其精确解成为孤子理论的一个重要的课题[6-8].离散的时间演化方程族合适的等谱问题是这一课题的一个难点.本文设计了一个新的等谱问题,根据相容性条件,推导出其Lax可积的非线性离散的晶格方程的正族和负族.最后,利用迹恒等式建立了它们的Hamilton结构.
考虑如下离散的矩阵等谱问题:

这里
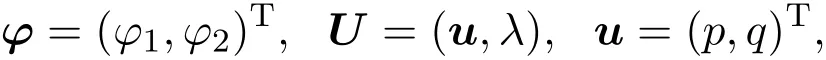
其中p=p(n,t),q=(n,t)是关于n和t的位势函数,n∈Z,t∈R,λ是谱参数.令f=f(n)是一个离散的函数,如果E,E−1,D满足下列关系:
Ef(n)=f(n+1),E−1f(n)=f(n−1),Df(n)=f(n+1)−f(n−1)=(E−1)f(n),n∈Z.则称E是一个平移算子,E−1是它的逆算子,D是一个差分算子.
下面根据相应的时间谱矩阵Γ的不同情况,利用等谱问题(1)可以推出两个不同的可积方程族,分别称为正族与负族.
2 正的离散晶格方程族

可以获得下列方程:

令

并把它们代入(2)式,可得


其中Θ=1+pq.根据文献[1],容易证明am+1,bm,cm,m≥0都是局域的.
令

通过比较λ的次数,容易得到:

取Vm=V+,根据离散的零曲率方程Utm=(EV(m))U−UV(m),可以获得Lax可积的离散方程族:

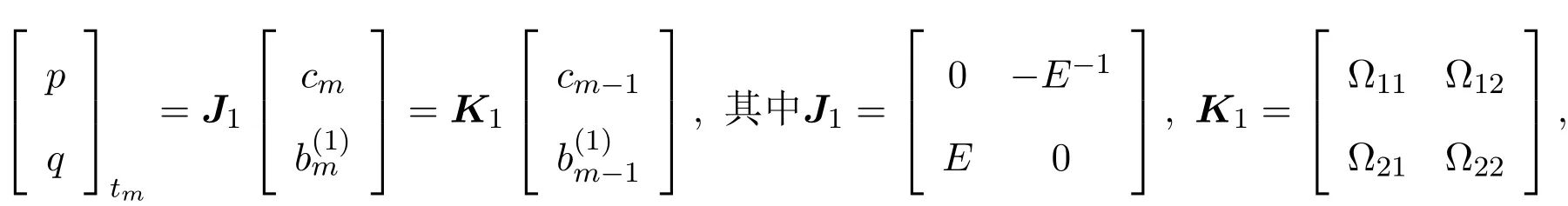
且

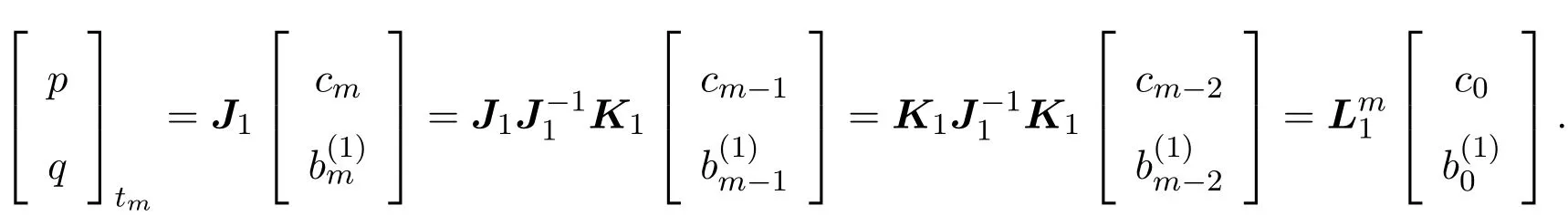
下面讨论方程族(6)的Hamilton结构.
令

计算得
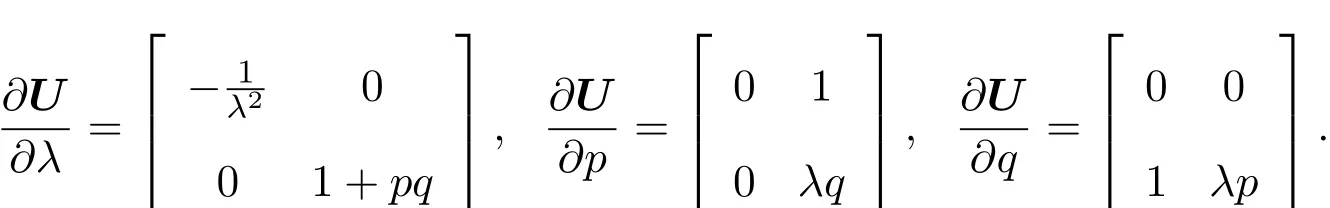
记〈A,B〉=tr(AB),这里A,B是方阵,“tr”表示方阵的迹.经计算可得:

根据迹恒等式

可得:
比较上式两边λ−2m+1的系数,得
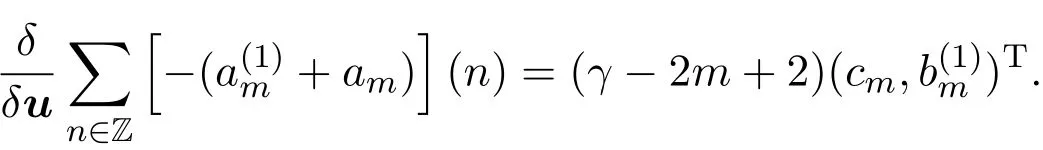
为了确定常数γ的值,上式两端取m=0,可得γ=−2.从而(6)式可写为:
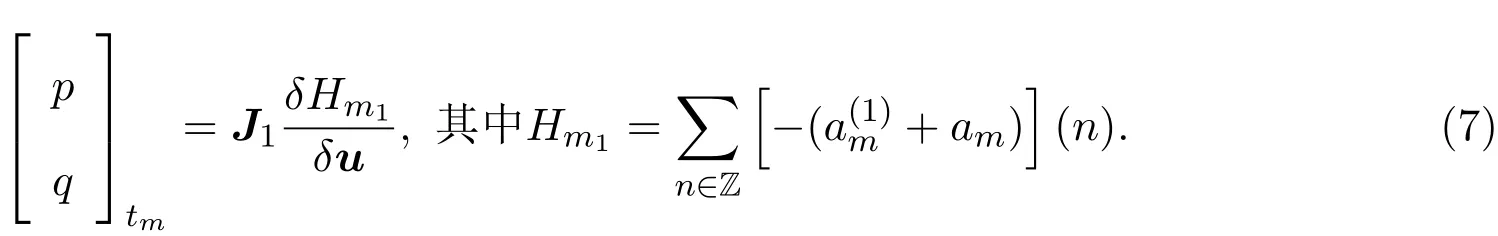
方程族(7)是在关系式(4)中λ次数为正号的情况下推导出来的.因此,称此方程族为正的离散晶格族.
3 负的离散晶格方程族
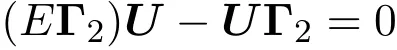
可以获得下列方程:
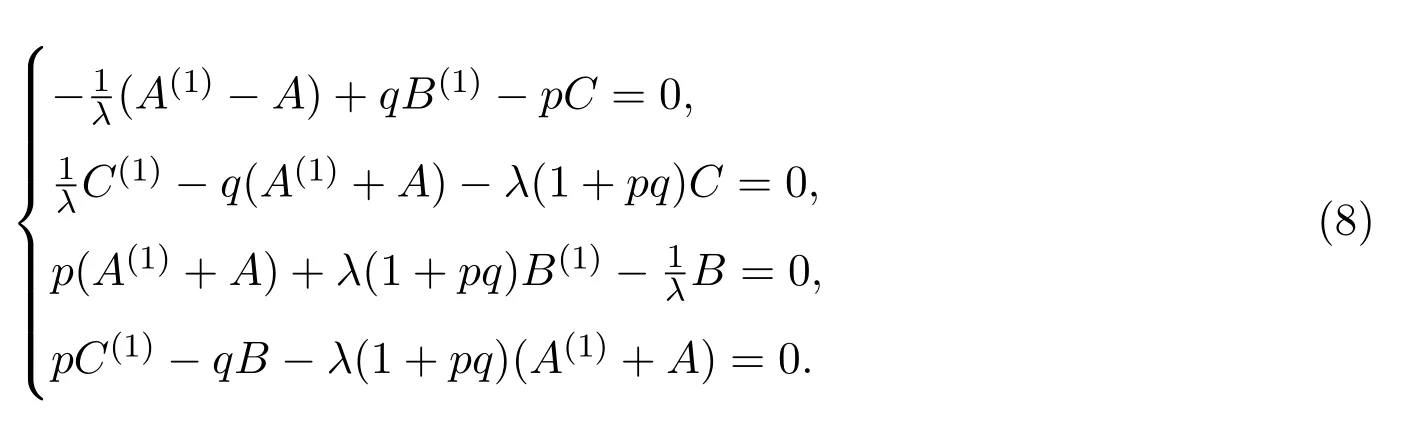

令

并把它们代入上述方程,可得
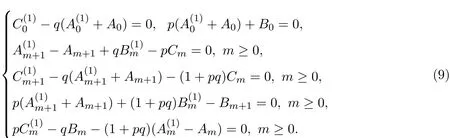

利用递推关系(9),可以依次获得:

根据文献[1],容易证明Am+1,Bm,Cm,m≥0都是局域的.
令
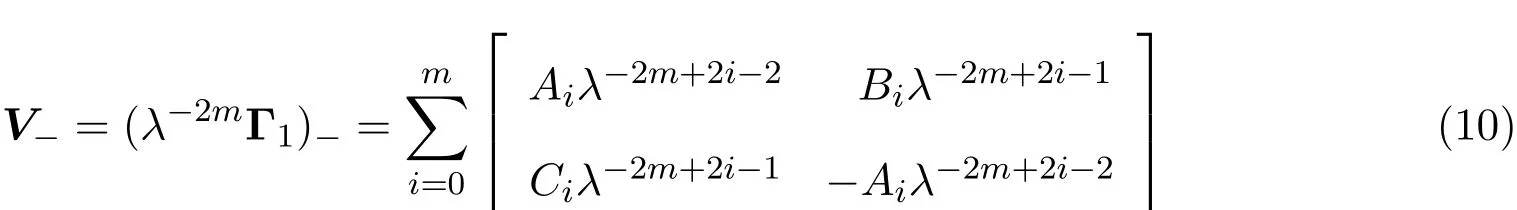
通过比较λ的次数,容易得到:

为了导出零曲率方程,选取修正项取∆m=则

取Vm=V−+∆m,则有
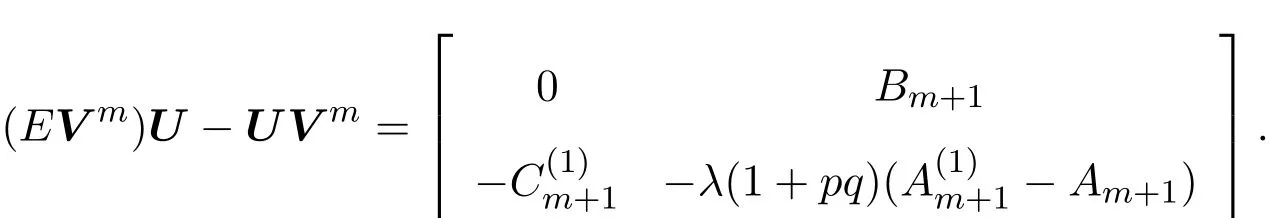
根据离散的零曲率方程Utm=(EV(m))U−UV(m),可以获得Lax可积的离散方程族:

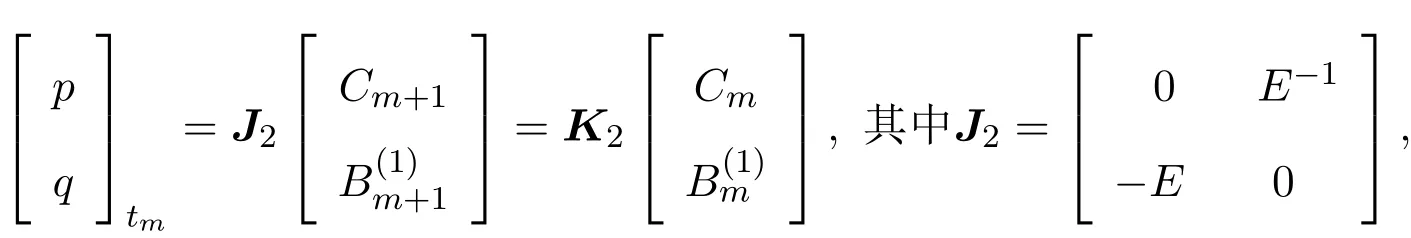


下面讨论方程族(12)的Hamilton结构.
利用迹恒等式,通过运算可得:
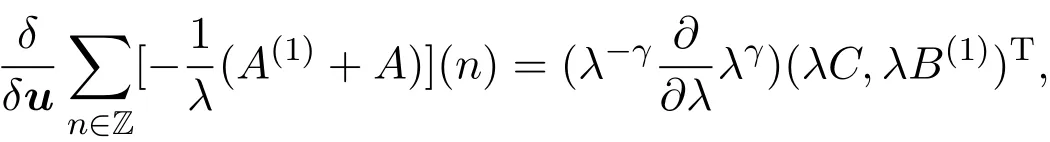
比较上式两边λ2m−1的系数,得

为了确定常数γ的值,上式两端取m=0,可得γ=1.从而(12)式可写为:
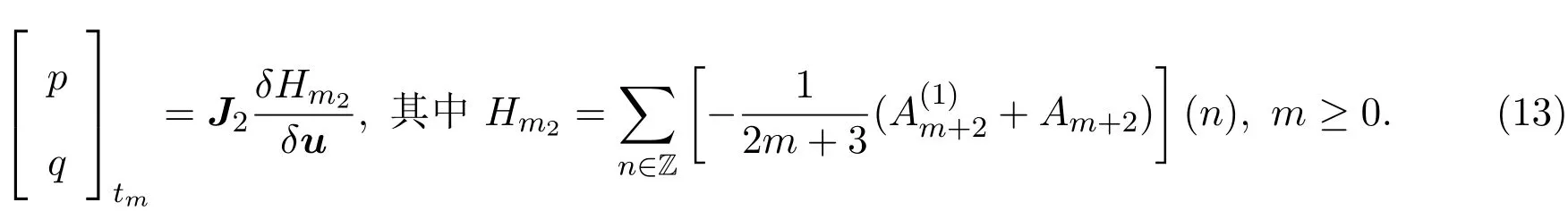
而方程族(13)是在关系式(10)的次数为负的情况下推导出来的,因此称这个方程族为负族.
通过新构造谱问题(1),本文推导出两个可积的方程族(6)和(12),并利用迹恒等式建立了它们的Hamilton结构(7)和(13).
参考文献
[1] Tu Guizhang.A trace identity and its applications to the throry of discrete integrable systems[J].J.Phys. A:Math.Gen.,1990,23:3903-3922.
[2] 陈登远.孤子引论[M].北京:科学出版社,2006.
[3] Zhang Yufeng,Yan Wang.A higher-dimensional Lie algebra and its decomposed Subalgebras[J].Physics Letters A,2006,360(1):92-98.
[4] Xu Xixiang.A hierarchy of discrete Hamiltonian equations and its binary nonlinear by symmetry constraint[J].Physics Letters A,2004,326:199-210.
[5] 常双领.一个新的Lie代数和它的应用[J].纯粹数学与应用数学,2013,29(6):627-633.
[6] Fu Jingli,Song Duan,Fu Hao,et al.Symmetries and conserved quantities of discrete wave equation associated with the Ablowitz-Ladik-Lattice system[J].Chinese Physics B,2014,22(9):1-6.
[7] 行姗,勾明,时振华.一类非线性时间演化方程的新的行波解[J],纯粹数学与应用数学,2011,27(2):220-224.
[8] 闻小永.一个离散晶格方程的N波Darboux变换和无穷守恒率[J],数学的实践与认识,2012,42(13):246-252.
A discrete positive hierarchy and a negative hierarchy as well as their Hamilton structures
Chang Hui,Qu Zhe,Tao Keqin
(Department of Mathematics,Qingdao Binhai University,Qingdao266555,China)
A new discrete spectral problem in the paper is devised,whose compatibility condition gives rise to a new positive hierarchy and a negative hierarchy of discrete integrable equations.Making use of the trace identity, their Hamiltonian structures are worked out respectively.The Darboux translation,bilinear form,symmetries, conservation laws,conserved quantities and their exact solutions of the resulting equation hierarchies are worth investigating in the future.
lattice equation,positive hierarchy,negative hierarchy,trace identity,Hamiltonian structure
O175
A
1008-5513(2014)05-0496-07
10.3969/j.issn.1008-5513.2014.05.010
2014-07-04.
山东省自然科学基金(ZR2011AQ017,ZR2010AM028).
常辉(1978-),硕士,讲师,研究方向:可积系统与精确解.
2010 MSC:45G15

