全平面内随机Dirichlet级数的几个定理
谭洋
(中国人民大学信息学院,北京100872)
全平面内随机Dirichlet级数的几个定理
谭洋
(中国人民大学信息学院,北京100872)
利用Nevanlinna理论研究了全平面内随机Dirichlet级数所表示的整函数的增长性和值分布,得到全平面内水平带形上的几个新的定理,推广了以往研究半平面内水平半带形上关于增长性和值分布的一些相关结论.
随机Dirichlet级数;增长级;值分布;Picard点
1 引言
关于随机Dirichlet级数的值分布,国内外学者进行了大量的研究,取得了一系列重要成果(参考文献[1-9]).本文通过对全平面内随机Dirichlet级数所表示的整函数的增长性和值分布的研究,得到结论:对于{Xn(ω)}(n=0,1,2,···)是独立同分布的随机Dirichlet级数在任何水平带形意义下的a.s.增长性与其在全平面内的a.s.增长性相同,对于无穷级随机Dirichlet级数a.s.在任何水平带形的边界上都存在Picard点.对于{Xn(ω)}(n=0,1,2,···)是独立非同分布的随机Dirichlet级数在一定条件下的a.s.增长性与其在全平面内的a.s.增长性相同.
2 预备知识
本文的符号除特别说明外均参考文献[10-12].
定义2.1设{Xn(ω)}(n=0,1,2,···)是概率空间(Ω,A,P)上的一个复随机变量序列,设非负数序列{λn}(n=0,1,2,···)满足:
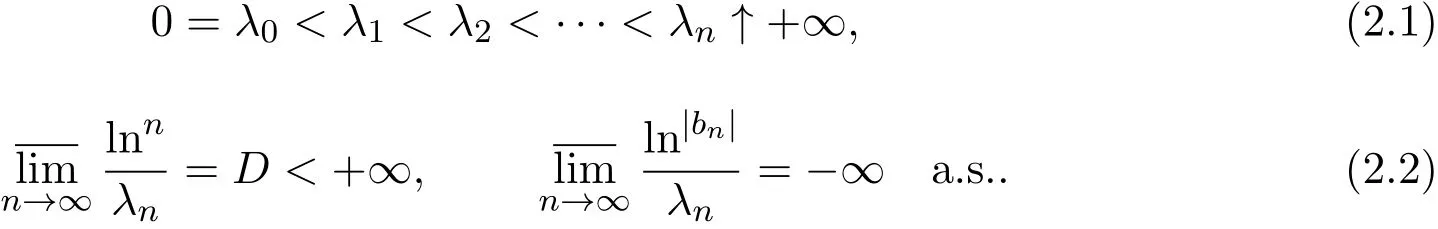
那么
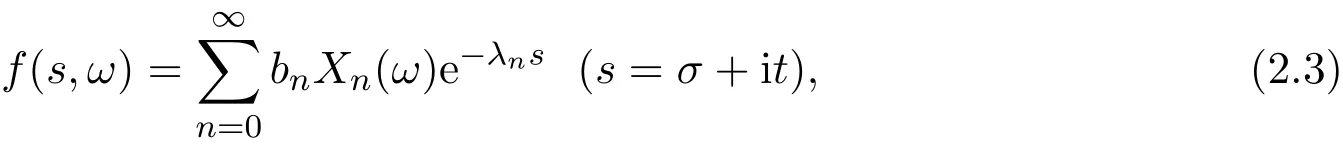
表示全平面内的随机Dirichlet级数,这里σ及t都是实变量.
本文中{Xn(ω)}均为独立的.为了方便,引入辅助Dirichlet级数.
定义2.2设级数
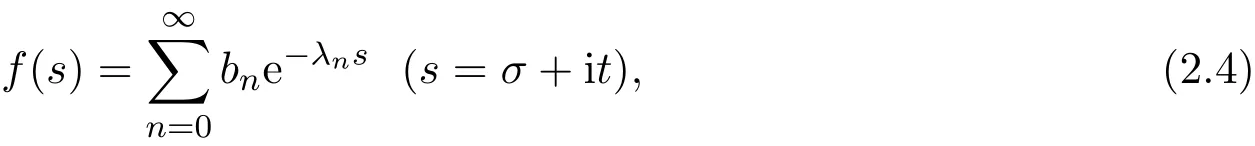
满足条件(2.1)和(2.2),那么级数(2.4)表示全平面内一个Dirichlet级数,这里σ及t都是实变量.
令
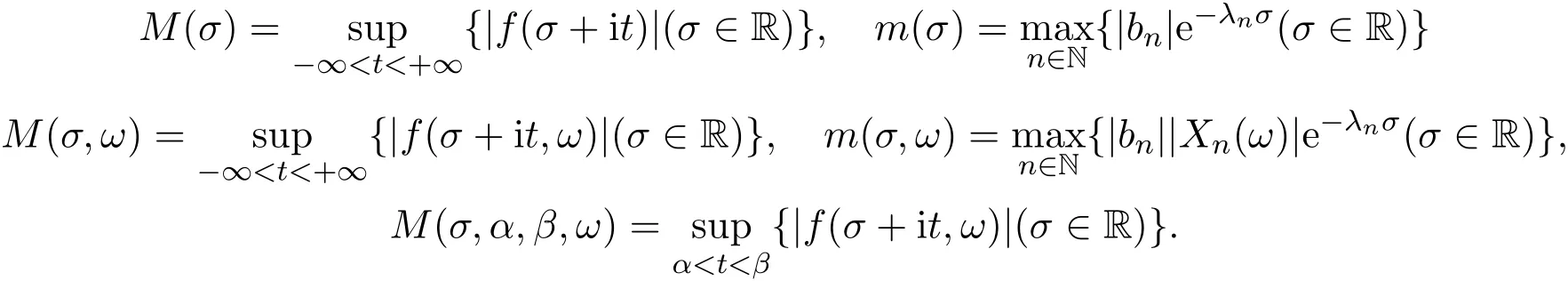
定义2.3Dirichlet级数f(s)与随机Dirichlet级数f(s,ω)的级分别是
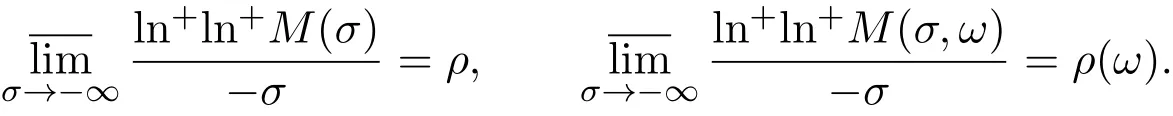
引理2.1[11]设c为一正的常数,x是任一正实数,那么函数

引理2.2[11](Paley-Zygmund)设{Xn(ω)}(n=0,1,2,···)是概率空间上的独立同分布的随机变量序列,数学期望满足E(Xn)=0,方差满足E(|Xn|2)=θ2>0,则对任意的H∈A,存在
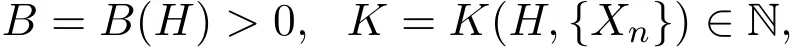
使得对任何复数列{bn}⊂C及任何自然数p与q,p>q≥K,恒有
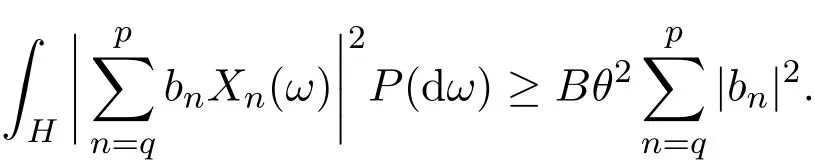
引理2.3[11-12]设级数(2.4)满足条件(2.2),则有下式成立:
引理2.4[11](Paley-Zygmund)设{Xn(ω)}(n=0,1,2,···)是概率空间上的独立非同分布的随机变量序列,数学期望满足E(Xn)=0,方差满足则对任意的存在
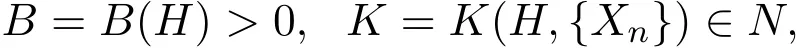
使得对任何复数列{bn}⊂C及任何自然数p与q,p>q≥K恒有
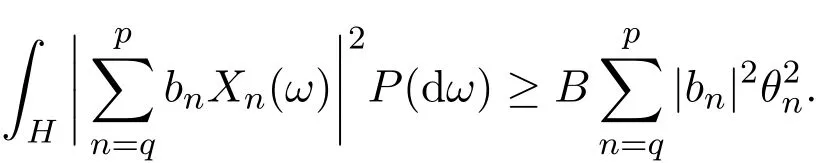
引理2.5[12](Valiron)设函数ψ(z)在|z|<1内解析,并且成立,其中M(r,ψ)=max{|ψ(z)|:|z|=r<1}.那么在|z|=1上必有一点z0,在它的任何邻域内,ψ(z)取任何复数值无穷多次,至多有一例外值.z0称为ψ(z)的一个Picard点.
3 主要结果
定理3.1设λn及bn满足条件(2.1)和(2.2),{Xn(ω)}(n=0,1,2,···)是概率空间(Ω,A,P)上的独立同分布的随机变量序列,那么f(s,ω)a.s.具有下列性质:对任意的实数α及β(α<β),
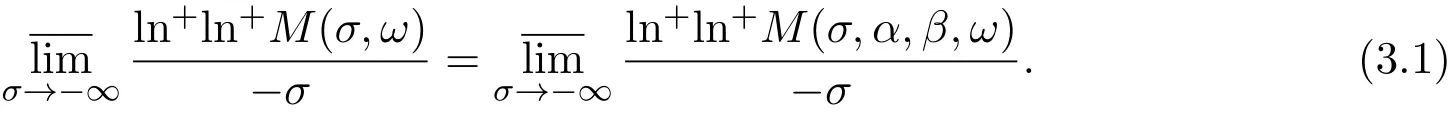
定理3.2设f(s,ω)为无穷级随机Dirichlet级数,λn,bn及{Xn(ω)}(n=0,1,2,···)满足定理3.1中的条件,那么f(s,ω)具有下列性质:在全平面中任何水平带形的边界上一定存在Picard点.
定理3.3设λn及bn满足条件(2.1)和(2.2),{Xn(ω)}(n=0,1,2,···)是概率空间上的独立非同分布的随机变量序列,满足:
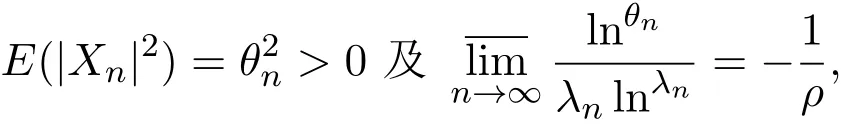
那么f(s,ω)a.s.具有下列性质:对任意的实数α及β(α<β)有下式成立:
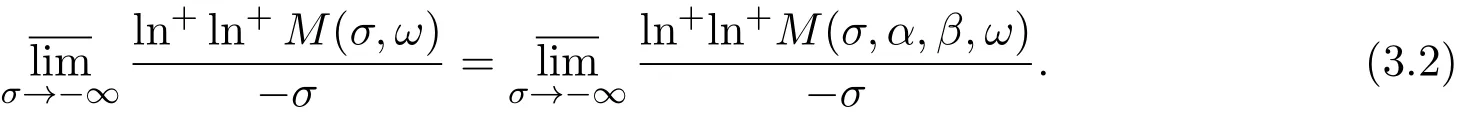
推论3.1对于满足定理3.3的条件的非同分布的随机变量也有定理3.2的结论.
4 定理的证明
4.1 定理3.1的证明
设(3.1)式的左边的上极限等于ρ a.s..当ρ=0时,(3.1)式是显然成立的.
设0<ρ≤+∞,假定Ω中有一概率大于零的事件E,相应的有一个正数ρ′(<ρ),使得对于ω∈E以及某两实数α及β(α<β),有

那么当σ→−∞且α 由引理2.2,对充分大的N,有 所以,当−σ充分大,n≥N时,有 在(4.2)式两边同时除以λnlnλn,则有 即 与引理2.3矛盾,所以命题得证. 4.2 定理3.2的证明 假定Ω中有事件E,P[E]>0对于ω∈E及某一复数s0=σ0+it0与某一正数ε(<π),假设f(s,ω)在水平带形的边界上没有Picard点,假设水平带形是以t0为中线宽为2ε的水平带形,作变换 通过上述变换得到: 令 设 则可计算出 对于无穷级随机Dirichlet级数,由级数的定义,有 由定理3.1,有 则取{σn}→−∞的子列,仍记为{σn},使 取{sn=σn+itn,|tn−t0|<ε,σn∈},使得 又因为 即 若 其中ρ为有限数,则 即 矛盾,所以有 成立.则由引理2.5可知,f(s,ω)在水平带形的边界上一定有Picard点,所以假设不成立,命题成立. 4.3 定理3.3的证明 设(3.2)式的左边的上极限等于ρ a.s..当ρ=0时(3.2)式是显然成立的. 设0<ρ≤+∞,假定Ω中有一概率大于零的事件E,相应的有一个正数ρ′(<ρ),使得对于ω∈E以及某两个实数α及β(α<β),有 那么当σ→−∞且α 则有 由引理2.4,对充分大的N,有 所以当−σ充分大,n≥N时,有 在(4.4)式两边同时除以λnlnλn,则有 即 则与引理2.3矛盾,所以命题得证. 参考文献 [1] 余家荣.Dirichlet级数与随机Dirichlet级数在水平直线上的增长性[J].江西师范大学学报,1995,19(3):189-196. [2] 孙道椿,高宗升.无限级随机Dirichlet级数的值分布[J].数学年刊,1993,14:677-685. [3] 孙道椿.半平面上的随机Dirichlet级数[J].数学物理学报,1999,19(1):107-112. [4] 孙道椿,陈特为.无限级Dirichlet级数[J].数学学报,2001,44:259-268. [5] 孙道椿.Dirichlet级数的级[J].华南师范大学学报,2001,3:14-20. [6] 邓冠铁.Dirichlet级数表示的整函数的增长性[J].北京师范大学学报,2002,38(2):156-159. [7] 刘素红,田宏根.Dirichlet级数的增长性[J].纯粹数学与应用数学,2013,29(3):264-274. [8] 杨乐.值分布及其新研究[M].北京:科学出版社,1982. [9] Tsuji M.Potential Theory in Modern Function Theory[M].Tokyo:Maruzen,1959. [10] 余家荣.随机狄里克莱级数的一些性质[J].数学学报,1978,21:97-118. [11] 余家荣,丁晓庆,田范基.Dirichlet级数与随机Dirichlet级数的值分布[M].武汉:武汉大学出版社,2004. [12] 余家荣.狄里克莱级数与随机狄里克莱级数[M].北京:科学出版社,1997. Several theorems of random Dirichlet series Tan Yang By Nevanlinna theory we study the growth and distribution of the entire function expressed by a random Dirichlet series on the whole plane.We get several new theorems in the horizontal strip on the whole plane.We extend some relevant results of the growth and distribution of the entire function expressed by a random Dirichlet series in the half horizontal strip on the half plane. random Dirichlet series,the growth,the value distribution,Picard points O178 A 1008-5513(2014)05-0512-08 10.3969/j.issn.1008-5513.2014.05.013 2014-04-27. 国家自然科学基金(11171013). 谭洋(1979-),博士生,研究方向:函数论. 2010 MSC:30D30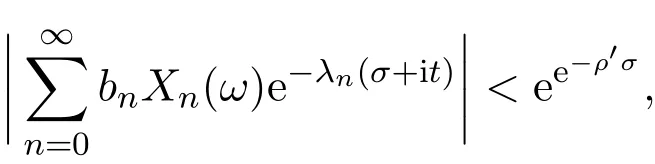
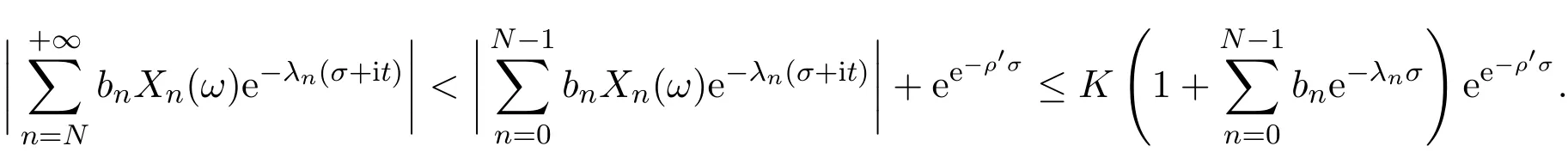
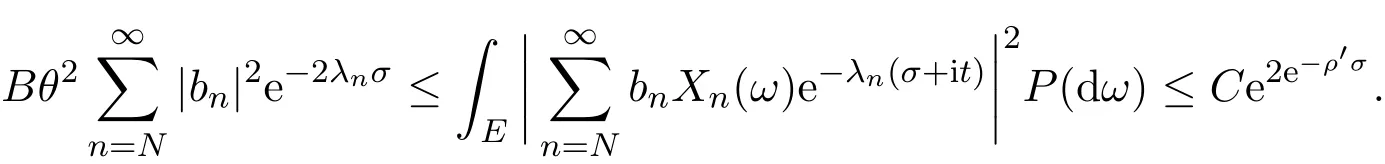
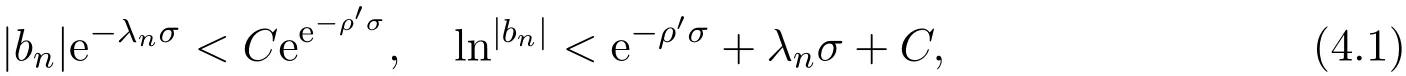
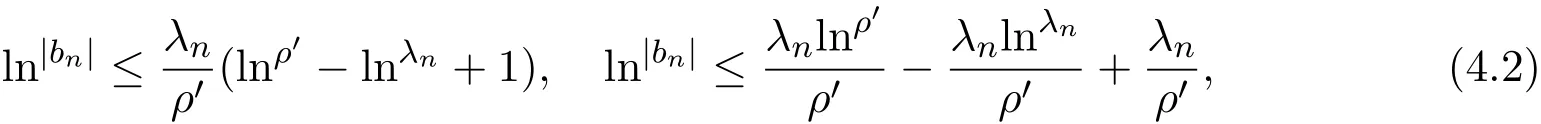
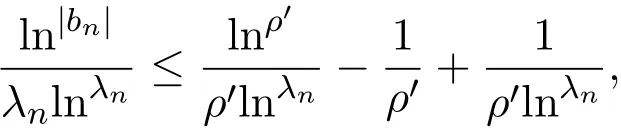

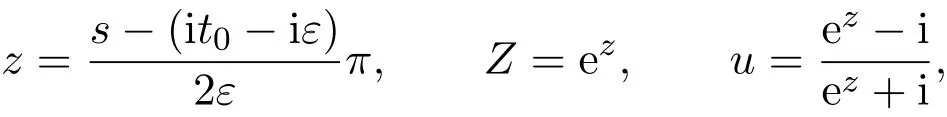

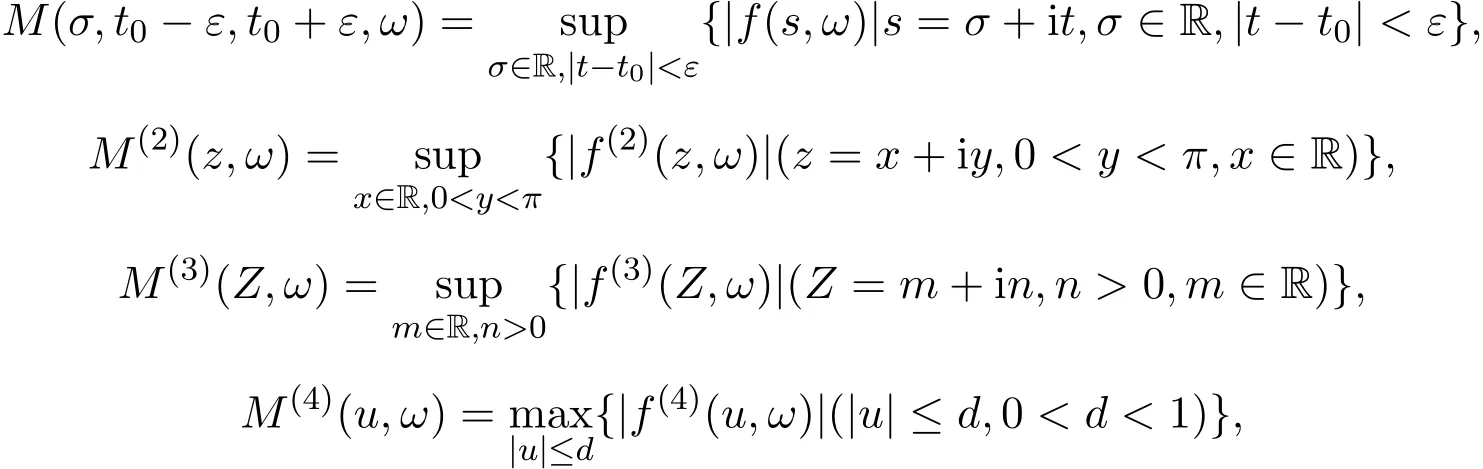
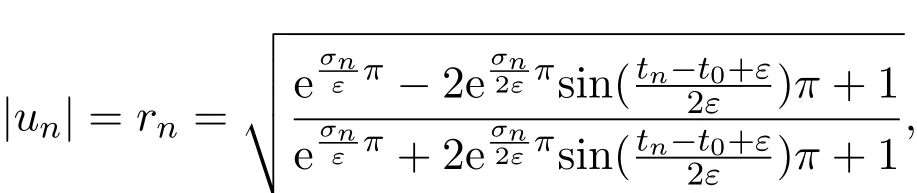
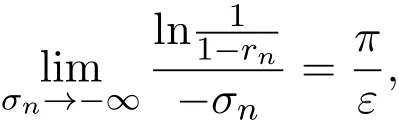
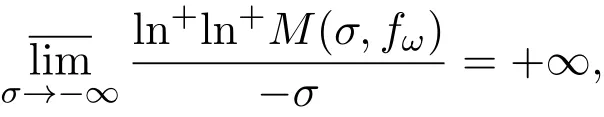
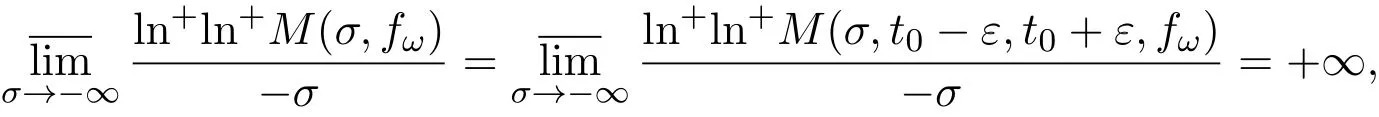
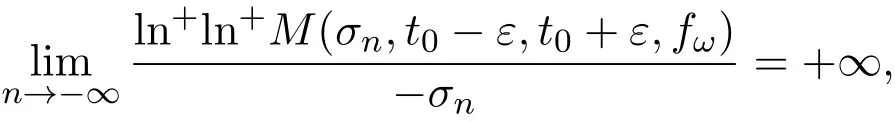
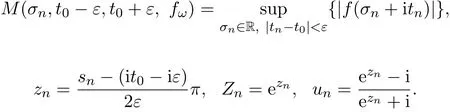

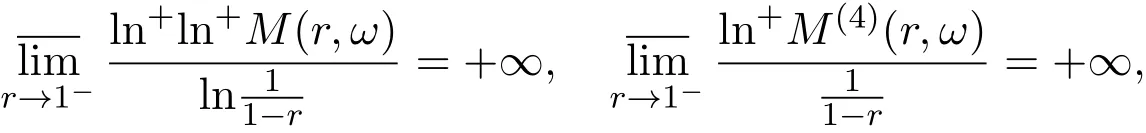
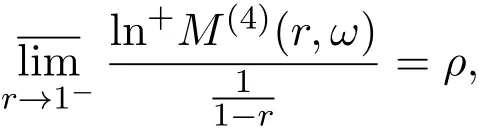
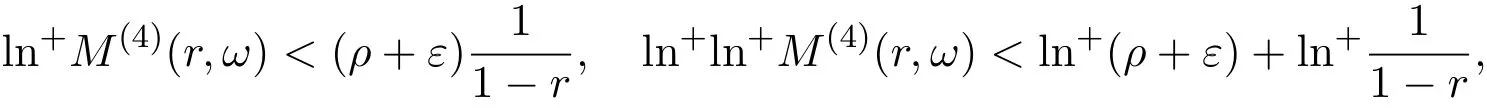
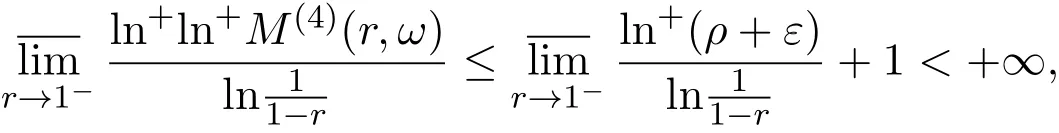
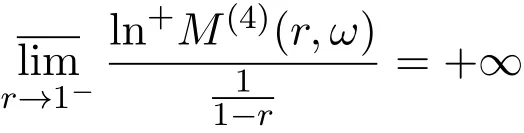
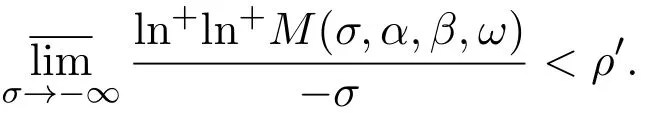
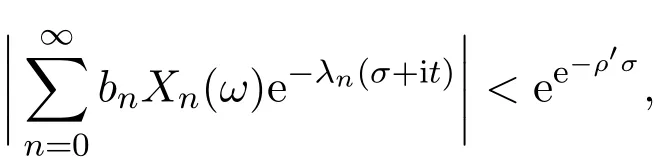
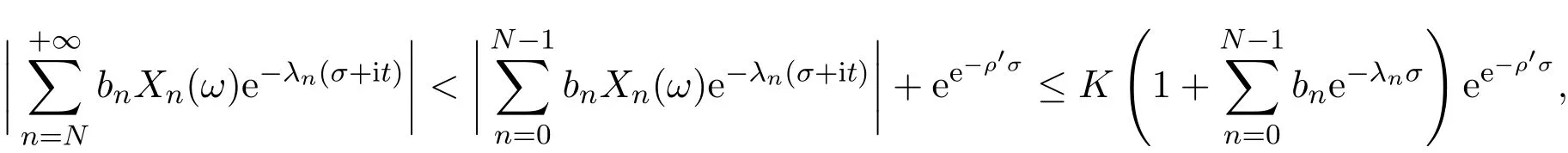

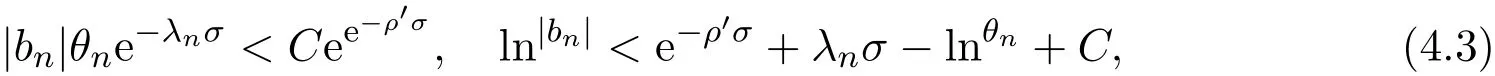

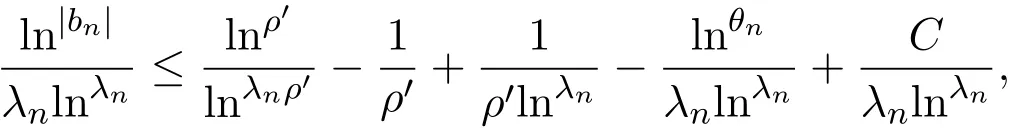
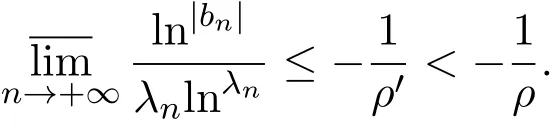
(School of Information,Renmin University of China,Beijing100872,China)

