康普顿效应问题中“度”的把握
丁德生
(江苏省兴化中学,江苏 兴化 225700)
“度”是处理量变、质变规律问题的关键.很多的物理问题涉及多方面的因素哪一个才是主要的?条件又如何?光的本性就是这类一个典型问题.光的本性从17世纪初光的波动说与微粒说之争开始,至20世纪初以光的波粒二象性告终,前后共300多年的时间.一方面光在空间传播时是一份一份的,表现为粒子性;另一方面光子分布的概率呈现波的特点,所以光又具有波动性(概率波).光子能量与动量的关系式也显示波动和粒子二象性是一个有机的整体.光的波动性与粒子性的表现是不平衡的,这种表现的不平衡与光的波长(或频率)有关,波长越长(或频率越低)波动性越明显,波长越短(或频率越高)粒子性越显著.然而这样的描述仍太模糊,如电磁辐射与物质相互作用时,可能会发生若干种不同的效应,这些效应是不同能量的光子与物质中的分子、原子、电子、原子核相互作用的结果,且这些效应发生的概率与入射光子的能量有密切关系.这类问题的处理要求对具体发生的各种效应的波长(或频率)有一个定量的判据,倘若不能把握这个“度”,定量的处理光的波动性与粒子性问题就无从谈起.光的波动性与粒子性的问题很多,本文仅用光子与电子相互作用的康普顿效应这一现象来浅析几个“度”的把握问题.
1922~1923年康普顿研究了X射线被较轻物质(石墨、石蜡等)散射后光的成分,发现散射谱线中除了有波长与原波长相同的成分外,还有波长较长的成份.这种散射现象称为康普顿散射或康普顿效应.图1为康普顿效应实验装置示意图,康普顿将0.71Å的X光投射到石墨上,然后在不同的角度测量被石墨分子散射的X光强度.当θ=0时,只有等于入射频率的单一频率光.当θ≠0(如45°、90°、135°)时,发现存在两种频率的散射光.一种频率与入射光相同,另一种则频率比入射光低.后者随角度增加偏离增大.而根据经典电磁理论,散射光波长应是不会改变的,为了解释这一现象,康普顿大胆地用光子与静止电子的弹性碰撞的模型(如图2)来解释散射光波长(或频率)的改变,得出了波长(或频率)移动的公式,理论上计算出X射线在石墨中散射后波长(或频率)的改变量与实验测量值完全吻合,成功地解释了这一现象,为此人门就把这一散射现象称为康普顿散射或康普顿效应.康普顿效应与光电效应一起成为光的量子论的重要实验依据.

图1

图2
康普顿效应是高中物理选修3-4模块中说明光具有粒子性的重要内容.各种考试(如高考)频频涉及,更有些高端的考试(如名牌大学自主招生等)要求学生能从定量、半定量的层面上处理康普顿效应问题,学生更是觉得所学内容的不足.为此本文准备从定量层面通俗、简便地讲解康普顿效应问题,以期学生在通俗但更加深入地把握其中“度”的过程中起到抛砖引玉的作用.
1 多长的光子波长才能发生明显的康普顿效应呢?
康普顿用光子与静止电子的弹性碰撞模型来解释散射光波长的改变,过程推导如下.
如图3光子的能量为hν0、动量为光子与静止电子碰撞后,把一部分能量传给电子,散射光子能量为hν、动量为而电子发生了反冲,电子反冲速度为u,考虑相对论效应电子动量为是电子的静止质量.

图3
碰撞过程动量的变化如图3,由动量守恒定律可得

由能量守恒定律可得

由(1)、(2)式可得

(康普顿效应波长移动关系)
结论1:式(3)表明,散射光波长与散射角θ有关,而且散射光的波长总是大于入射光波长.
小小飞机达到一定高度后,便俨然如降落伞盘旋而下,依然落在场中一角,可以重新拾起,且重新派它向上高升。或当发放时稍偏斜一点,它的归宿处便改了地方,有时随风扬起挂在柳梢上,有时落在各种小摊白色幕顶上,有时又凑巧停顿在或一路人草帽上。它是那么轻,什么人草帽上有了这小东西时,先是一点儿不明白,仍然扬长向在人丛中走去,于是一群顽皮小孩子,小狗般跟在身后嚷着笑着,直到这游人把事弄明白,抓了头上小东西摔去,小孩子方才争着抢夺,忘了这或一游人,不再理会。
结论3:λc=2.42631×10-12m与入射光的波长无关,且波长的移动是10-12m量级,而要观察到这种效应散射光波长有明显的改变(相对入射波长)才有意义,由此(3)式中入射光的波长应与λc数量级相当,即当光子的能量hν~106eV(约1MeV),才能观察到明显康普顿效应的“频移”.
实验表明光子能量较低时 (hν<0.5MeV),以光电效应为主;高能γ光子 (hν>1.02MeV)可以与原子核发生作用,产生正负电子对;当入射光子具有中等能量(0.5MeV<hν<1.02MeV)时,产生康普顿效应,实验结果与前面的理论推导的3个结论完全吻合.当然这也就是当初康普顿用与λc相当的X射线来做实验能够观察到明显“频移”效应的原因.
例1.在康普顿效应中,求:(1)反冲电子获得的最大动能Ekmax与入射光子能量hν0的关系式;(2)入射光子的能量在什么范围内,康普顿效应才能显著?
解析:(1)由上面结论可知

当θ=180°时散射光子能量与原光子的能量差最大,此时反冲电子获得的最大动能(Ekmax),由能量守恒定律得
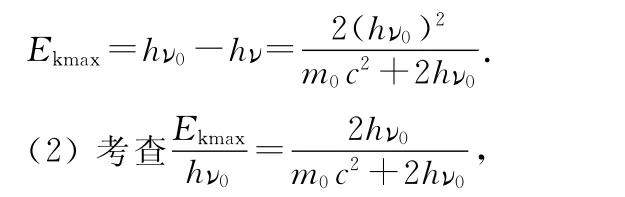
显然上述比值越大康普顿效应越显著,所以hν0~m0c2=0.51MeV,才 是 明 显 康 普 顿 效 应 的 “度”.例 如,hν0=m0c2=0.51MeV时相当明显了.
点评:本题从电子被碰撞获得的最大动能Ekmax与hν0的关系出发得出明显康普顿效应的条件,hν0~m0c2=0.51MeV与实验结果是一致的.过程推导简洁,结论明确,说服力强.
2 要考虑相对论效应吗?
上面的推导过程考虑了相对论效应,结果更一般、适用范围更广,但表达式也更复杂,难度也大.相对论效应对结果影响究竟有多大,能否略去相对论效应简化处理呢?下面笔者用一道有趣的考题来说明.此例为2013年南京大学强化班自主招生的一道考题,不少学生在这道考题上出了问题,两种解法结果不同,谁对呢?
例2.一初始能量为Ei的光子射向一静止的质量为m0的电子(此过程可看成质点碰撞模型),碰后光子能量变为Ef,以与原入射方向成θ角射出,试导出Ei,Ef,θ,m0,光速c之间的关系式.
解法1.(考虑相对论效应)利用上面的结论得
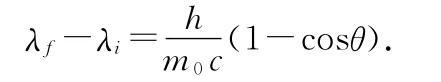
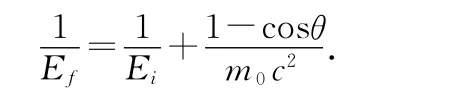

由能量守恒定律得

由以上两式得

反思1:两种解法结果是不一样的,表面来看很难确定哪一种解法正确.它们都运用了动量守恒定律和能量守恒定律,不同之处就在于是否考虑相对论效应的问题,解法1中应用的相对论效应,而解法2没有考虑,两种不同的表达式计算结果是否接近呢?其实要不要考虑相对论效应关键在于反冲的电子速度是否可与光速比拟,而这种能否比拟必须建立在定量计算的基础之上.
以下用实际发生明显康普顿效应的条件进行分析.
应用例1的结果光子电子碰撞后,反冲电子的最大动能为

若Ekmax=0.5MeV,
从上面无论(1)、(2)得到的u都是跟光速可比拟的,必须要考虑相对论效应,所以解法2是错误的.
反思2:康普顿效应说明了光的粒子性,康普顿散射的理论和实验完全一致,在更加广阔的频率范围内更加充分地证明了光子理论的正确性;而在公式推导中引用了动量守恒定律和能量守恒定律,再次证明了微观粒子相互作用过程也遵循这两条基本定律.
总之,本文通过定量的推导、计算,给出处理相关问题“度”的定量数值,讲解通俗、简便,定位准确,印象深刻,收到了较好的效果,同时也充分展示了数字的力量.
1 卢德罄.大学物理学[M].北京:高等教育出版社,2003:379-380.

