基于MATLAB的HTM50200异型石材车铣加工中心横梁结构拓扑优化设计及实验研究

穆璇，张珂，赵德宏，吴玉厚

(沈阳建筑大学交通与机械学院，辽宁沈阳110168)

结构拓扑优化设计是在初始结构关系未知的情况下，以寻求结构的材料在设计空间最佳传力路径而展开的结构拓扑优化技术的研究，在结构的概念设计阶段具有很重要的指导性意义。目前出现了一系列具有连续拓扑设计变量的优化模型，主要包括［1］:均匀化法、变密度法、进化结构优化方法，独立映射法，水平集法等。其中变密度法由于设计变量少、迭代效率高、易于实现等优点而得到了广泛关注。

目前变密度法中最为流行的插值方法有各项同性惩罚微结构模型法 (SIMP)和材料属性有理近似模型 (RAMP)［2］。1988年 BENDSOE等提出的基于均匀化理论的结构拓扑优化设计，开创了连续体结构拓扑优化设计研究的新局面［3］。

SIMP法是由 MLEJNEK等［4］于1993年提出的，1999年BENDSOE等［5］将其进一步发展，并且证明了该方法物理意义的存在性。在前人提出的重要理论基础上，后人也将其跟其他现代设计方法相结合，衍生出了其他一些拓扑结构优化方法，如左孔天等［6］用拓扑优化方法进行了微型柔性机构的设计研究，罗震［7］用变密度法详细研究了连续体结构的拓扑优化设计。文中利用SIMP法对龙门机床横梁进行拓扑优化设计。

龙门机床的横梁是一个极其重要的部件，它起着支撑滑鞍工作头、连接立柱床身等关键部件的作用，并在加工过程中带动工作头实现加工中心的纵向进给，故横梁的动力学特性直接影响整机的精度与动力学特性。HTM50200龙门式车铣加工中心为专门针对复杂异型石材制品加工开发的一种八轴五联动数控加工加工中心，如图1所示［8］。

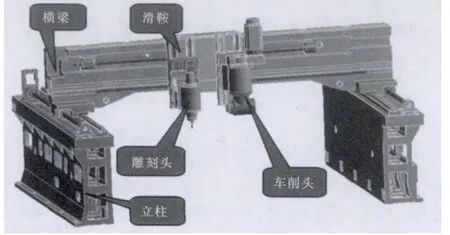
图1 HTM50200虚拟样机

1 基于变密度理论的优化模型

1.1 优化模型的建立

以结构整体刚度最大也等价于结构的总变形能最小为目标，以材料体积为约束条件，建立拓扑优化的设计模型:

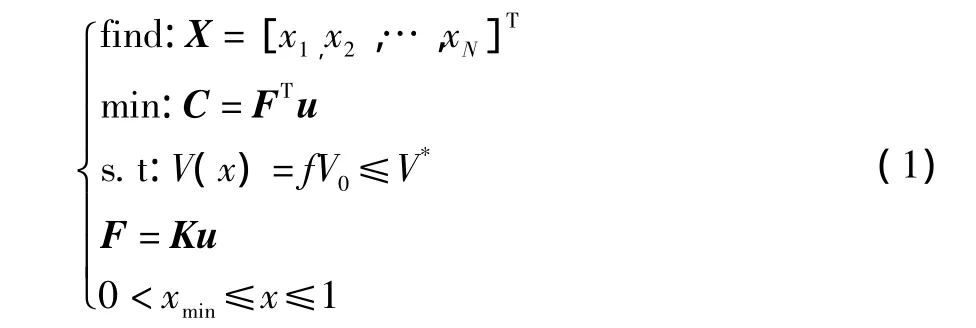
式中:C为结构的柔顺度;X为设计变量，材料的相对密度，表示在区间 ［0，1］上有多少存在的单元;F为载荷向量;u为节点位移向量;N为单元总数;V0表示整个设计域初始体积;V*为体积上限;f为优化体积比;V(x)为优化后结构体积;K为总体刚度矩阵。

有限元结构中存在关系式:

式中:Ve为优化后的单元体积;xe为单元设计变量柔度，可以写为:

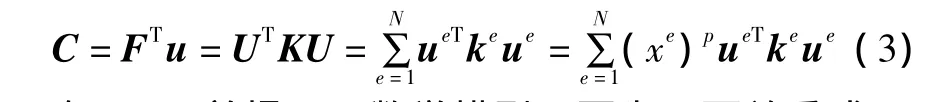
在SIMP前提下，数学模型可写为下面关系式:

1.2 优化求解方法

优化准则法是在20世纪60年代后期发展起来的一种可以替代数学规划法的结构优化设计方法，准则法最初的基本思想见于Michell在1994年发表的文献［9］中。准则法 (又称OC方法)一般适用于单目标、单约束条件下的优化问题求解，很少使用敏度分析信息，计算速度快，并且计算规模与求解变量的数目无关，故拓扑优化中的优化算法一般情况下采用优化准则法。人们把数学中最优解应满足的Kuhn-Tucker(库恩-塔克)条件作为结构优化设计的准则，形成所谓的理性准则法。Kuhn-Tucker条件的引入，增强了准则法的数学基础和通用性，并使准则法最终得到优化问题的局部最优解甚至全局最优解成为可能。针对该优化问题构造相应的拉格朗日函数为:

式中:λ1，λ2，λ3，λ4为拉格朗日乘子，当x=x*时取极值，拉格朗日函数应满足的Kuhn-Tucker必要条件为:

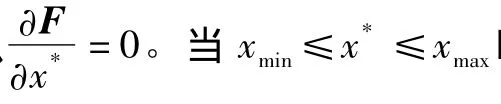
对于上式等于0的情况，并且由C=UTKU可得:

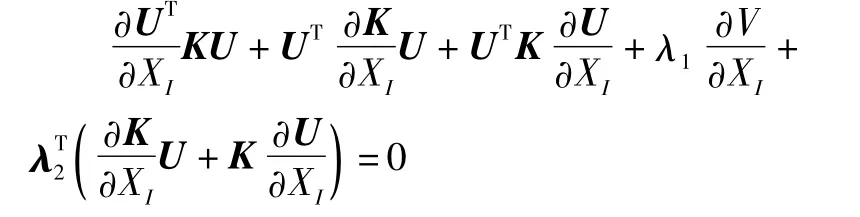
把Ke=(xe)pK0，g(x)=fV0= ∑Ne=1xeVe代入上式，并且利用结构刚度矩阵的对称性可得:

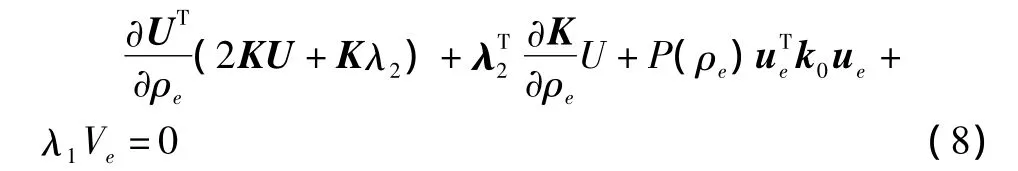
不妨取λ2=－2U代入上式得

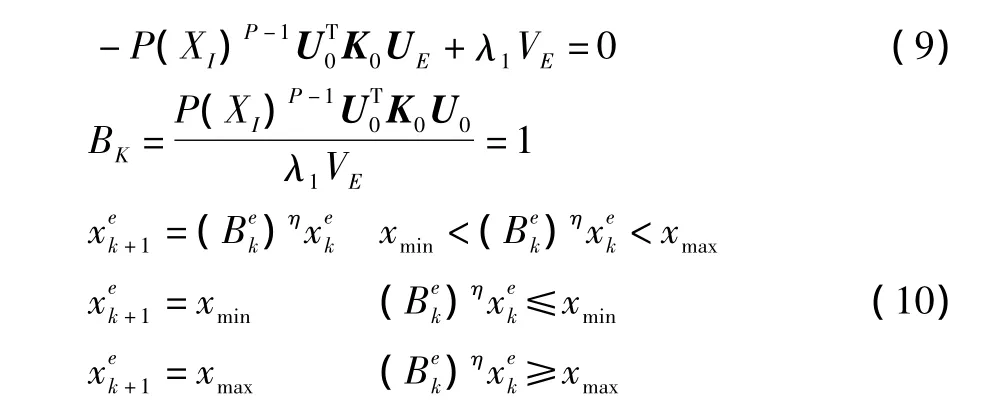
式中:η为阻尼系数，引入η的目的是为了确保数值计算的稳定性和收敛性。

1.3 惩罚因子对设计结果的影响

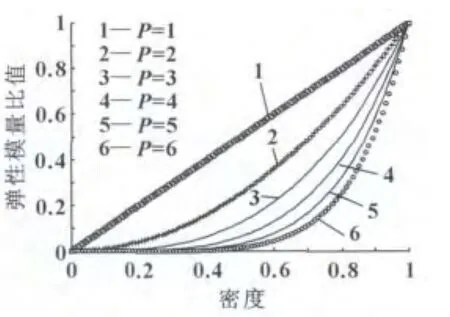
图2 SIMP模型密度同弹性模量间关系

将惩罚因子引入SIMP密度函数插值模型，在材料的弹性模量和单元相对密度之间建立起一种对应关系。它的作用是推动设计变量的值 (文中指密度)逐渐向0、1两端聚集，从而可以得到更加清晰的拓扑形式。SIMP法的惩罚曲线如图2所示，当P=1.0时成线性关系，即没有惩罚效应，很显然P值越大，惩罚效果越好。

然而在实际运用中如图3所示，SIMP法有明显的缺点［1］:(1)理论上SIMP模型并不能保证惩罚函数是一个凹函数，不能取得全局最优解;(2)当P取值大于某值后，其优化结果没有如理论上所述的加以改进，反而可能得到完全误导性的结果。通过运行MATLAB发现，P值越大迭代次数越多，收敛的时间越长，不利于计算，因此惩罚因子不宜选过大。文中选惩罚因子P=3时的结果，从而得到最优拓扑结构。

图3 不同惩罚因子下的优化拓扑图

2 龙门横梁的拓扑优化设计

以HTM50200车铣加工中心横梁截面为研究目标，结构如图1所示。横梁采用双直线导轨形式，上面导轨水平布置，下面导轨竖直布置，能有效地承担来自滑鞍和工作头的在竖直与水平方向的载荷。龙门机床的横梁工作时承受复杂的空间载荷。横梁部件在工作时所承受的力有加工时产生的切削力、自身重力、移动部件和固定部件相对运动时导轨面间的摩擦力、联结大件和移动部件间的联结力、惯性力、冲击或震动干扰力以及温度升高时产生的热应力［10］。而优化过程中应设置为机床常态下的负载条件，因此横梁受到自身重力——均布载荷，滑鞍及上面组件的重力——集中载荷的作用。

图4 部分纵截面横梁模型

由于横梁纵截面太长，计算效率低下，浪费时间，故节选一部分为研究对象，对其进行受力分析，优化效果如图4所示。

横截面模型为简便起见，采用结构左右下角固定约束，上、下面模拟导轨结点受向下重力F1、F2作用，材料惩罚因子取值为3，敏度过滤半径为2，体积比为0.4，结构离散为80×60个四结点四边形有限单元。截面算例如图5所示。在MATLAB帮助下，用SIMP法计算出的最优拓扑的模型如图6所示。

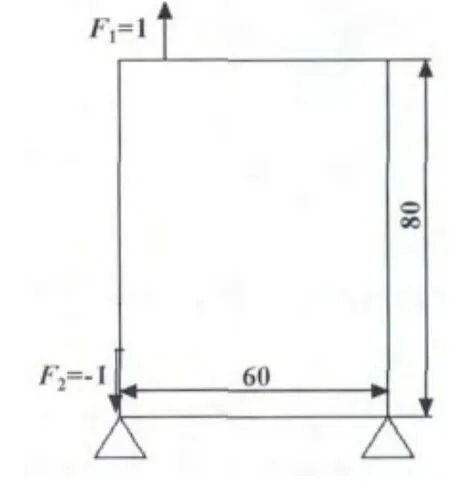
图5 横截面模型

图6 结构拓扑图

从图6可以看出:所获得的拓扑图形具有一定的参考意义，可从中得出横梁截面筋肋的布局:整体采用“之”字形排布。根据结果设计横梁如图7所示，横梁总质量9 377 038g，比传统结构减轻2.75%。

图7 横梁内部筋板布局

3 试验分析

3.1 试验设备

在这次试验中，主要采用的仪器和分析系统有东方所生产的 INV3018C、DASP-V10模态分析模块、ICP型输入方式的加速度传感器和朗斯公司生产的LC1031力锤及其配套的力传感器，如图8及表1所示。

图8 实验设备

表1 试验模态测试所用设备

3.2 试验方法

在将试验数据导入DASP-V10模态分析模块之前，首先在信号相干性大于0.8以上的前提下，将激振信号和响应信号进行FRF分析，即传递函数分析，然后通过模态分析［11］系统对传函曲线进行定阶拟合，最后识别出结构的模态参数，即测试对象的固有频率值及各阶振型。具体试验流程如图9所示。

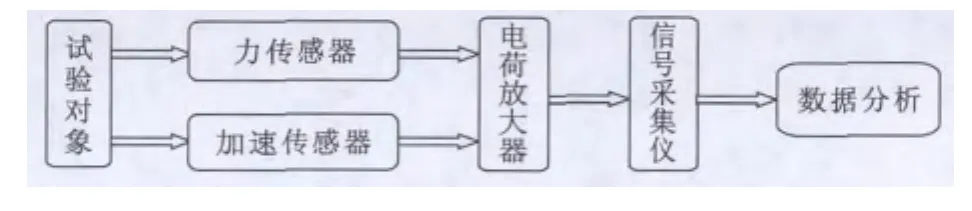
图9 试验模态测试流程示意图

3.3 模态试验

该试验的验证过程:首先用力锤在横梁上某一点处激振，同时用加速度传感器在主轴端部拾取响应信号，将这两路信号分别导入数据采集系统;然后交换激励点和响应点，读取这两路信号，比较前后两组数据。

3.4 试验与数据分析

试验之前，先将滑鞍移到横梁中间部位，复合式工作头调整到实际加工时的位置，然后用力锤敲击靠近刀具的主轴端部，并用5个加速度传感器分别拾取机床各个测量点的响应信号。通过采集分析系统记录下X和Y方向上的频响函数 (图10—11)、相干函数等，为下一步的定阶、曲线拟合提供必要的数据。

图10 横梁上X方向上随机两点的频响函数曲线

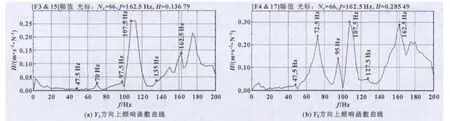
图11 横梁上Y方向上随机两点的频响函数曲线

3.5 试验结果分析

从表2可以看出:实验结果与仿真分析值的误差在10%以内，说明仿真分析数据真实可靠，之所以产生误差可能的原因有:

(1)建立有限元模型时，省略了零部件倒角、螺栓孔等。

(2)仿真软件分析时使用的材料属性及参数设置的准确性对分析结果造成了影响。

(3)试验时激励位置和测试点的选择及锤击的脉冲信号存在少许误差。

(4)测量时传感器本身的误差或是安装误差会给试验结果带来影响。

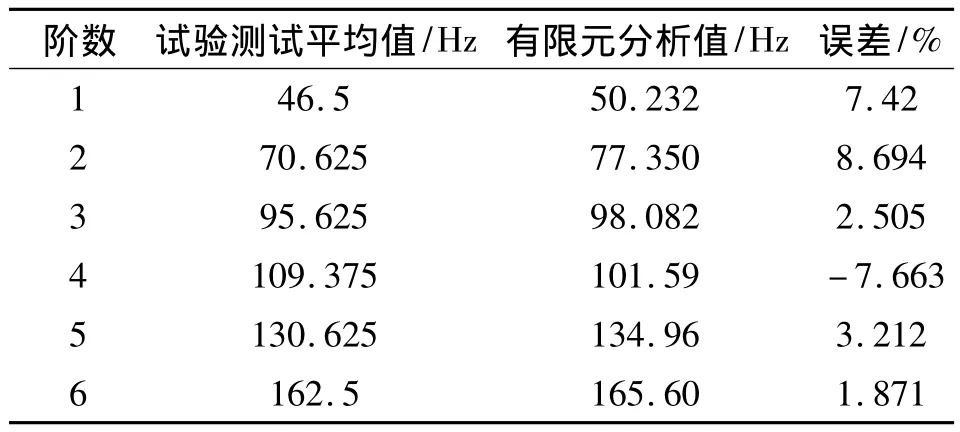
表2 横梁模态测试与仿真结果对比值

4 结论

(1)通过推导拓扑优化中变密度法数学模型，用MATLAB实现了HTM50200车铣复合加工中心横梁筋肋的设计，比传统结构减轻2.75%。

(2)试验与仿真分析表明，该结构有良好的动力学特性。

［1］陈祥，刘辛军.基于RAMP插值模型结合导重法求解拓扑优化问题［J］.中国机械工程，2012，48(1):135－140.

［2］隋允康.建模·变换·优化——结构综合方法新进展［M］.大连:大连理工大学出版社，1996.

［3］BENDSOE M P，KIKUCHI N.Genrating Optimal Topologies in Structural Design Using a Homogenization Method［J］.Computer Methods in Applied Mechanics and Engineer，1998，71:197 －224.

［4］MLEJNEK H P，SCHIRRMACHER R.An Engineer's Approach to Optimal Material Distribution and Shape Finding［J］.Computer Methods in Applied Mechanics andEngineering，1993，106:1 －26.

［5］BENDSOE M P，SIGMUND O.Material Interpolation Schemes in Topology Optimization［J］.Archive of Applied Mechanics，1999，69:635 －654.

［6］左孔天，陈立平，王书亭，等.用拓扑优化方法进行微型柔性机构的设计研究［J］.中国机械工程，2004，15(21):1886－1890.

［7］罗震.基于变密度法的连续体结构拓扑优化设计技术研究［D］.武汉:华中科技大学，2005.

［8］兰利洁，崔正兴，张珂，等.异型石材车铣加工中心立柱及导轨精度调试与分析［J］.沈阳建筑大学学报:自然科学版，2012，28(2):358 －362.

［9］MICHELL A G M.The Limit of Economy of Material in Frame Structure［J］.Philosophical Magazine，1994，8(6):589－597.

［10］王晓煜，贾振元，杨凡，等.龙门加工中心横梁部件的拓扑优化设计与分析［J］.制造技术与机床，2009(11):64－68.

［11］吴玉厚，吴岗，张珂，等.异型石材多功能数控加工中心关键部件的模态分析［J］.沈阳建筑大学学报:自然科学版，2009，25(1):165－169.