铁道车辆液压减振器联合仿真模型的构建及其试验验证

肖乾，李清华，王成国，张海，，徐红霞，贾慧芳

(1.华东交通大学载运工具与装备教育部重点实验室，江西南昌330013;2.中国铁道科学研究院铁道科学技术研究发展中心，北京100081)

液压减振器是铁道车辆悬挂系统的重要阻尼元件，它通过节流的方式吸收和缓和道路不平顺等引起的振动和冲击，达到提高车辆安全性、平稳性及舒适性的目的。随着乘客对列车安全性及舒适性的要求不断提高，研究减振器性能对车辆动力学性能的影响显得尤为重要。因此，有必要借助计算机仿真技术建立液压减振器联合仿真模型，以期为其嵌入车辆模型研究减振器性能对车辆动力学性能影响建立基础。

目前，国内外学者对于液压减振器数学模型的建立方法归纳起来有3种，即参数化建模、等效参数化建模、非参数化建模。参数化建模因考虑了减振器内部油液流动以及节流阀弹性元件的变形等真实工作状态而应用较多［1］。对于减振器建模大多忽略其两端的橡胶元件而做了刚性处理，但已经有学者指出减振器节点刚度对其性能及车辆动力学性能有较大影响［2－3］。鉴于上述原因，以下将采用参数化建模的方法以高速列车KONI横向减振器为例，在Easy5环境下建立液压减振器液压控制模型。对建立好的液压减振器控制模型应用Easy5和ADAMS接口技术在ADAMS环境下建立考虑减振器橡胶节点刚度的Maxwell联合仿真模型并通过试验验证了模型的精确性。

1 减振器参数化建模

1.1 减振器的工作原理

KONI横向减振器其内部油液是单向流动的，在活塞和底座上都设有单向阀，在活塞杆导向座上设有阻尼调节阀。

如图1为单向流液压减振器拉伸和压缩工作情况。当活塞受到到拉伸力Fe作用时，减振器拉伸长度S，活塞单向阀关闭，活塞上部相当于体积为A的油液从拉伸腔通过阻尼调节阀流入储油缸，而底座上单向阀开启相当于体积为 (A+B)的油液通过单向阀流入压缩腔;当活塞受到压缩力Fe作用时，减振器压缩长度S，底座单向阀关闭，活塞单向阀开启，相当于体积 (A+B)的油液从压缩腔通过活塞单向阀流入拉伸腔。

图1 油液单向流动减振器工作原理

1.2 液压减振器液压流体力学基础方程

液压流体力学是流体力学的一个组成部分，主要研究液体与液压元件之间的相互作用规律。通过研究液体运动规律和流体运动与力的关系，推导出液体运动的连续性方程、能量方程以及动量方程等流体动力学的基本定律。能量方程加上连续性方程，可以解决压力、流速或流量及能量损失之间的关系;动量方程可解决流动液体与固体边界之间的相互作用问题［1，4］。

连续性方程式就是流体流动过程中的质量守恒定律的一种数学表达式，假设流体为不可压缩，则连续性方程为:

式中:u，v，w分别为x，y，z方向的速度分量。

伯努利方程是流体流动中以其特有的流动参数来反应能量守恒定律的一种表达式:

式中:z1，z2为液面的高度;p1，p2为液面的压力;v1，v2为液面的流速;hw为能量损耗;ρ为液体密度。

根据流体力学理论知识，当小孔的通流长度l与孔径d之比l/d≤0.5时称为薄壁小孔流。通过薄壁小孔的流量可以由下式求得:

式中:Q为流经薄壁小孔的流量;Cd为流量系数，一般取0.62～0.63;A0为孔口截面积;ρ为油液密度;Δp为薄壁小孔两端压力差。

当小孔的流通长度l与孔径d之比l/d＞4时，称为细长小孔流。孔的流量可以由下式求得:

式中:Q为流经细长小孔的流量;d为细长小孔的直径;η为液体的动力黏度;l为细长小孔的通流长度;Δp为细长小孔两端的压力差。

当小孔的流通长度l与孔径d之比l/d≤4时，称为管嘴流动。管嘴流动可以由下式表示:

式中:Q为流经管嘴的流量;Cv为流量系数一般取为0.82;a为孔口截面积;ρ为油液密度;Δp为流经管嘴两端的压力差。

当液流空间的高度比和宽度小得多时，就称为缝隙流动。缝隙流动可以由下式表示:

式中:Q为流经缝隙的流量;b为缝隙的宽度;h为缝隙的高度;η为液体的动力黏度;l为通流长度;Δp为流经缝隙的压力差。

1.3 减振器液压动力学模型建立

在减振器动力学模型建立中以KONI减振器结构(图2)及主要结构参数值 (表1)为建模依据，在Easy5下建立减振器液压系统模型如图3。

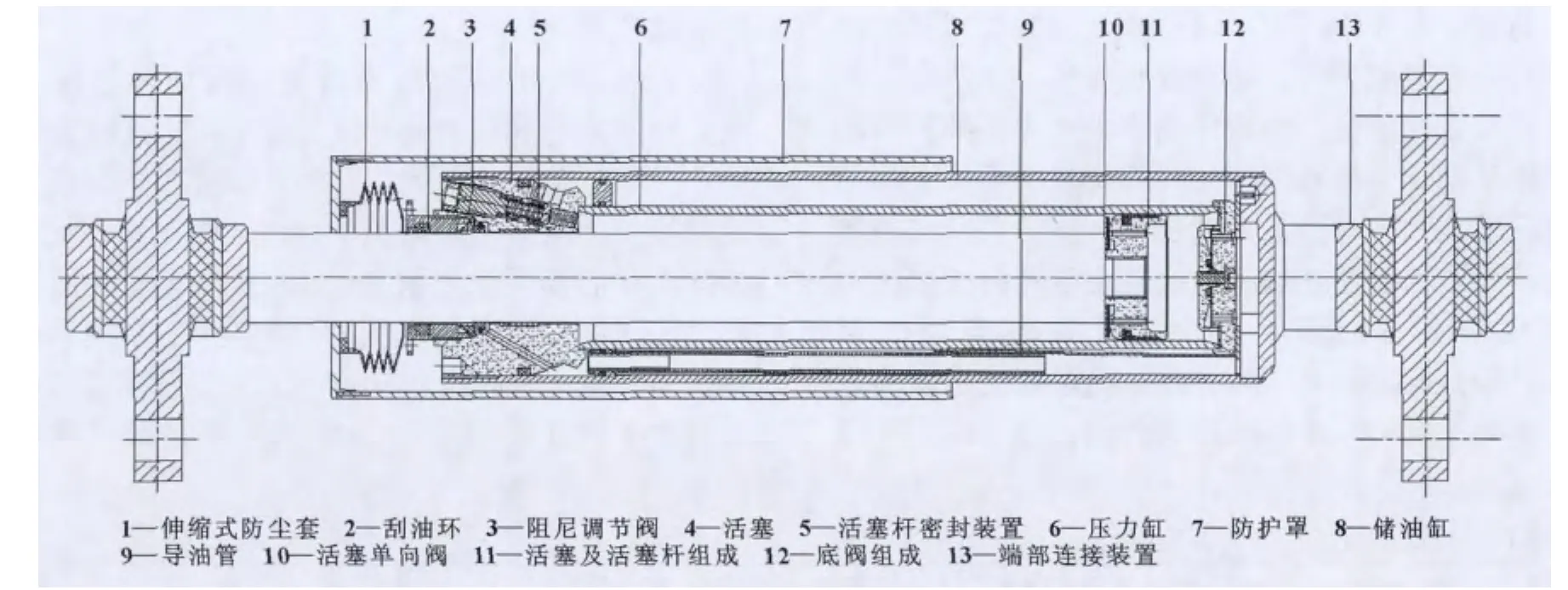
图2 KONI横向减振器结构图

表1 减振器主要结构参数值

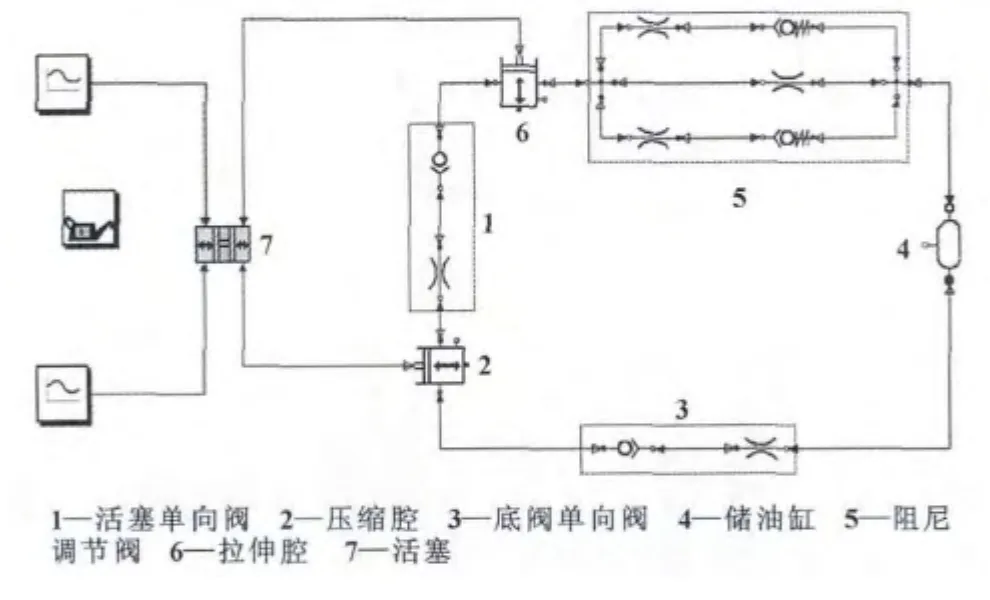
图3 减振器液压控制模型

模型中用提升阀元件与较大孔径节流孔元件串联与较小节流孔元件并联来模拟减振器阻尼调节阀。用单向阀元件与节流孔元件串联来模拟活塞单向阀和底阀。用两个变量容器元件来分别模拟拉伸腔和压缩腔。用液压缸元件来模拟工作缸、活塞和活塞杆。用蓄能器元件来模拟储油缸。

在不影响计算精度的情况下对模型做了如下假设:

(1)在整个工作过程中，减振器内的油液温度保持不变;

(2)不计压力变化引起的系统刚性构件的弹性变形;

(3)忽略工作过程中气泡产生的影响;

(4)不计油液自重;

(5)忽略活塞与工作缸之间、活塞杆与导向座之间的油液泄漏。

2 减振器联合仿真模型

铁道车辆上液压减振器的两端都因有橡胶连接结构(图4)而具有弹性刚度，该弹性刚度会使阻尼力与活塞速度及位移之间产生相位变化而影响减振器特性。因而在实际建模中常把减振器简化成一个阻尼和弹簧串联的组合元件，称为Maxwell模型。所以，以下将考虑减振器两端刚度建立Maxwell联合仿真模型。

图4 减振器两端橡胶连接结构

2.1 联合仿真模式的选择

对于Easy5和ADAMS的联合仿真模式主要有3种［5］(图 5):

(1)联合模式，由Easy5和ADAMS求解器求解各自的模型;

(2)控制系统导入模式，将Easy5所建立的控制与多学科系统导入ADAMS，利用ADAMS求解器积分计算所有的模型;

(3)函数评价模式，将ADAMS所建立的多体机械模型导入Easy5，利用Easy5求解器积分计算所有的模型。

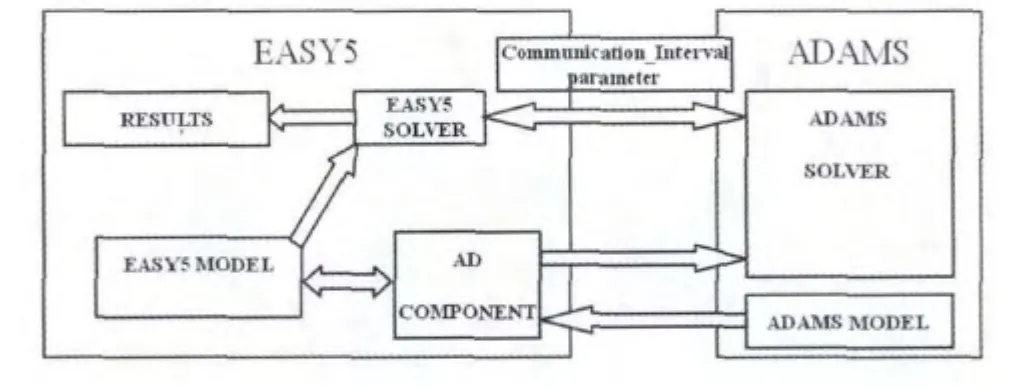
图5 联合仿真方式原理图

目前的学者们的研究都是采用控制导入模式进行仿真计算［6－8］，这主要是由于此种模式可以在控制系统预置参数的情况下研究整个模型的性能，采用ADAMS的参数评价功能进行统一的试验设计和参数优化。因此，在文中也将采用这种联合仿真模式进行建模分析。

2.2 联合模型实现过程

(1)在ADAMS中建立简化的减振器的机构模型，模型中将两端橡胶连接件等效为一个刚度为1.715×107N/m弹簧。定义活塞速度和位移为输出变量，阻尼力为输入变量，通过ADAMS/Controls模块将Control Plant输出，生成adm、cmd文件供Easy5配置接入。

(2)将建立好的减振器液压控制模型中添加ADAMS接口元件来替换原模型中位移和速度激励元件，在ADAMS接口元件中添加之前导出的adm、cmd文件从而实现与ADAMS机构模型的连接，然后导出dll文件。

(3)在ADAMS/View中通过Contol模块导入dll文件建立动态联合仿真模型，建立的简化模型如图6。

图6 减振器Maxwell联合模型

3 联合模型试验验证

图7 减振器外特性仿真曲线

为了验证减振器联合模型的准确性，分别在速度0.1 m/s、0.2 m/s、0.3 m/s、 0.4 m/s、0.5 m/s下进行仿真和试验。仿真结果如图7，试验结果如图8，仿真与试验结果对比如表2。

图8 减振器外特性实验曲线

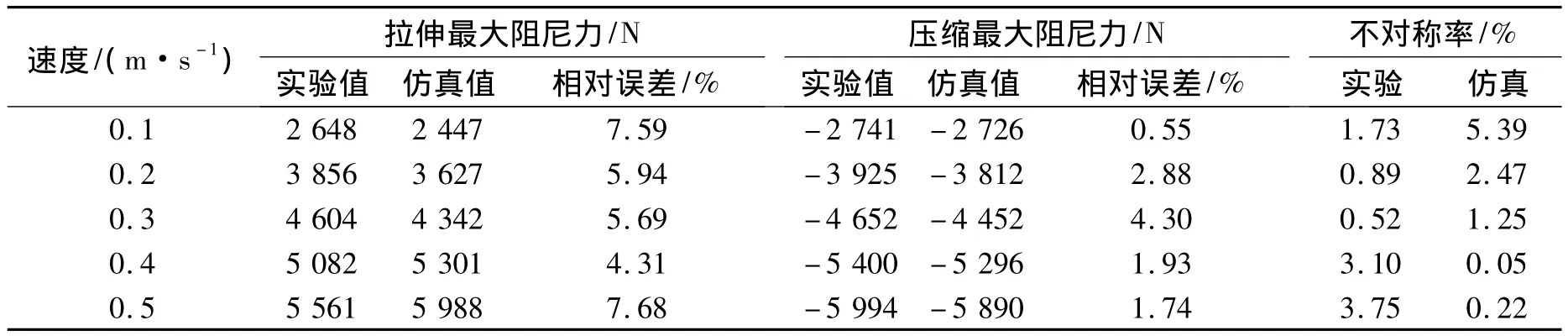
表2 实验与仿真结果比较

从表2可以看到，仿真拉伸阻尼力最大误差为7.68%，最小为4.31%;压缩阻尼力最大误差为4.3%，最小仅为0.55%。不对称率最大为5.39%，最小为0.05%，均小于机车车辆油压减振器技术条件［9］中对称率要小于10%的规定。由此可以说明所建立的模型较为精确可靠。

4 结论

以铁道车辆KONI横向液压减振器为例，根据其结构和工作原理，在考虑减振器两端刚度条件下成功建立了铁道车辆液压减振器的Maxwell联合仿真模型。利用建立的联合模型仿真计算分析了减振器的阻尼特性，并通过对比试验和仿真结果显示各项指标误差均小于10%从而验证了所建立的减振器联合模型较为精确。此联合仿真的建模方法适用于一般机液耦合问题的建模，为后期实现减振器嵌入车辆动力学模型提供了基础。

［1］孙胜利.位移相关减振器动力学建模及对车辆性能影响的研究［D］.长春:吉林大学，2008.

［2］陆冠东.串联刚度对液压减振器特性的影响［J］.铁道车辆，2007，45(2):1 －5.

［3］曾京，邬平波.减振器节点刚度对铁道客车系统临界速度的影响［J］.中国铁道科学，2008，29(2):94－98.

［4］徐灏.机械设计手册［M］.北京:机械工业出版社，1998.

［5］MSC Software Corporation Confidential.基于 Easy5/Adams的高压开关缓冲器分合闸动力学分析报告［OL］.

［6］李江波，黄明辉，赵兴.基于ADAMS与EASY5的大型模锻液压机联合仿真［J］.机械设计与制造，2011(6):235－237.

［7］生龙波，马吉胜，孙洋河，等.基于ADAMS与EASY5的某履带车辆制动系统的联合仿真［J］.机械制造，2012，50(574):28－30.

［8］陈北平，周新建.基于ADAMS与EASY5的双筒式液压减振器扫频研究［J］.机床与液压，2009，37(12):186 －188.

［9］中国人民共和国铁道部.TB/T 1491-2004.机车车辆油压减振器技术条件［S］.中国铁道出版社，2005.