基于三叉树期权理论的铁路货运定价模型

郭经纬，彭其渊

（西南交通大学交通运输与物流学院，成都610031）

基于三叉树期权理论的铁路货运定价模型

郭经纬，彭其渊＊

（西南交通大学交通运输与物流学院，成都610031）

将期权理论引入铁路货运定价活动，构建基于运输企业和期权客户期望最大化的多期三叉树定价模型，分析铁路运输企业的最优定价决策及期权客户的最优购买决策.研究结果表明：最优期权订购量是关于期权执行价格和期权价格的严格单调递减函数，而期权执行价格与现货市场运价、短期准备成本、无风险利率正相关，与长期准备成本负相关.通过算例的敏感性分析，发现当期权执行价格升高幅度超过10%时，期权客户的期权购买量下降梯度迅速增加，相比于期权价格，期权执行价格对期权客户的期权执行量具有更强的敏感性，因此铁路运输企业应关注期权执行价格的制定.

交通运输经济;期权定价；三叉树模型；执行价格；期权契约

1 引言

随着6月15日中国铁路总公司一系列实施货运组织改革措施的推出，铁路货运全面走向市场，努力为全社会提供更加方便、快捷的铁路货运服务，已成为中国铁路总公司企业性诉求的体现.目前我国的铁路运输中，除了少许受国家政策影响受特殊运输限制的货物外，大多数运输活动都已实现市场化经营，即运输活动伴随着契约市场和现货市场共存的现象.在契约市场中，铁路运输企业通过与契约市场客户提前签订包量协议（通常为半年以上）来销售一部分运力.这些契约的签订相对于交易稳定性较差的现货市场在稳定货源及运力方面具有一定优势，一方面为铁路运输提供稳定大宗货源，另一方面铁路运输企业为协议客户提供运力保证.但在契约期内，双方需执行固定的契约价格，不能在市场价格波动中获利，这对实现效用最大化是不利的.同时，铁路运输企业不会在契约市场将运力售罄，对于剩余运力，只能通过现货市场进行销售，而市场供求关系直接决定商品价格，而且价格存在较大波动，致使交易难以达成.随着供应链契约，特别是期权契约的深入研究，结合货运活动两种市场共存的现状，将期权契约引入铁路货运市场.研究如何应用其特点，制定有利于交易双方的最优决策问题就显得具有广泛的实际意义.

目前关于期权契约等各种供应链契约的文献很多.最早Pasternack利用报童问题从可退货的角度研究了契约的柔性问题[1].Emmons和Gilbe建立了带有回购机制的契约模型[2].Eppen等则在回购契约的基础上研究弹性契约对供应链绩效的影响[3].Tsay建立带有数量弹性的订购契约模型[4]. Barnes-Schuster等研究了需求具有相关性的供应链期权契约，并通过数值算例验证了期权契约在提高整个供应链效用中的作用[5].Cheng最早通过建立单周期、单品种二级供应链期权契约模型，确定双方的最优定价及订购策略[6].Wu等构建现货市场和契约市场并存的契约模型，并求出应购买的期权数量及第二阶段执行的期权数量[7].Stefan建立了在实体运输中合作伙伴通过期权合同达到风险共担和规避的模型[8].Wang和Tsao假设第二阶段执行的期权合同不等于第一阶段的期权购买量，从期权购买者的角度求出了最优策略[9].但将期权契约应用于货运业，大多集中于航海运输[10-12]，而在铁路货运业，仅有冯芬玲构建二叉树期权模型对铁路货运进行定价[13].虽然这些对研究铁路货运期权定价都具有一定的参考价值，但其对相关期权参数并未给出求解过程，只是进行简单假设；且模型简化价格变化，只粗略考虑价格上升和下降两种情况，难以解释价格未波动的情形.基于此，本文在前人研究基础上，为了更贴近现实情况，考虑上涨、下跌、运价未发生变化三类情形，构建基于运输企业和期权客户期望最大化的多期三叉树定价模型，设计求解相关期权参数，运用伊藤原理，求解相应的定价策略，以期为双方进行最优决策提供借鉴作用.

2 铁路货运期权设计

2.1 铁路货运期权定义

根据金融市场中期权的概念，结合铁路货运市场的具体特点，可设计并定义铁路货物运输期权如下：铁路货运期权是指以铁路货物运输服务为标的资产的一种期权合约，铁路运输企业是期权的制定方，期权客户即契约客户，是期权的购买方.如果到期日期权的执行价低于现货市场运价，期权客户会交付执行费并执行期权；反之，期权客户就会放弃期权的执行权而选择在现货市场中购买运力.这种选择权使得期权客户有效规避了价格波动风险.而对于铁路运输企业来说，在期权客户放弃执行期权时可以在现货市场中进行销售，并且可以收取一定的期权费用，从而可以将部分风险转嫁给期权客户，也有效实现了风险规避.

2.2 问题说明

本文假设铁路运输企业和期权客户都是经济人，均能做出理性决策，根据上述铁路货运期权的描述，引入期权机制后，铁路运输企业需推测期权客户的最优行动，从而制定合理的期权价格及执行价格；而期权客户则需根据铁路运输企业公布的定价及市场价格来决定期权的申购量和执行量，其决策过程实际上符合图1所示的两阶段动态博弈模型.

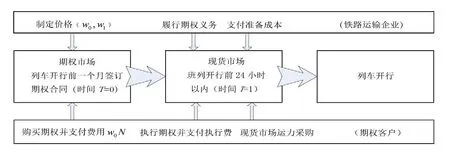
图1 引入期权的货运市场两阶段动态博弈模型Fig.1 Two-stage dynamic game model of freight market using option theory

将期权市场和与现货市场并存的铁路货物运输两阶段模型看做Stackelberg博弈，其中铁路运输企业为领导者，期权客户为跟随者，根据一般的Stackelberg博弈，跟随者首先做出有利于自己的最优决策，作为领导者的铁路运输企业则根据期权客户的最优决策来确定自身的最优决策，从而达到博弈的均衡.因此设计铁路货运期权交易操作顺序可表示如下：

（1）在时间T0的契约市场，铁路运输企业制定期权费用w0及期权执行价格w1；

（2）契约客户根据铁路运输企业的公示价格，在追求其自身预期收益最大化的同时，选择购买期权最优量N，并支付期权费用w0N；

（3）在时间T1的现货市场，契约客户根据现货市场运价wu、wd和期权执行价格w1，决定是否实行到期期权，并结合市场运力需求决策期权执行量及现货市场运力购买量，并支付相应费用，获取相应利润期望函数E(ξ)；

（4）铁路运输企业支付长期成本b1、短期成本b2及固定生产成本KC，并获得其利润期望函数E(ζ).

2.3 符号定义

w0表示期权费用（单位运力）；w1为期权执行价格（单位运力）；S0为时间t=0的现货市场运价（单位运力）；pu为现货市场运价上涨概率；pd为现货市场运价下跌概率；pm为现货市场运价保持不变的概率；wu为铁路货运期权到期日现货市场价格上涨时单位运力价格；wd为铁路货运期权到期日现货市场价格下跌时单位运力价格；u为现货市场单位运力上行乘数；d为现货市场单位运力下行乘数;u和d这两个乘数表示初始价值为S0的标的资产，经过t时间步长后，价值要么上升至uS0，要么下跌至dS0，其中0＜d＜1＜u；C为单位运力固定成本；b1为长期准备成本；b2为短期准备成本；K为铁路货物运输提供的总运力.

2.4 假设说明

（1）本文所涉及期权为欧式看涨期权，即铁路货运期权只能在到期日执行.

（2）铁路运输企业与契约客户是完全理性的，且两者均为风险厌恶者.

（3）在连续状态下，铁路货运价格在期权有效期[0,T]内遵循几何布朗运动，即其中：S(t)为t时刻的铁路货运价格；α为漂移率，即铁路货运市场收益率标准差；σ铁路货运运价波动率，代表期权有效期内对铁路货运市场收益率波动程度的度量；α和σ都与时间成比例，但对标的路径会产生不同影响，若时间区间较短，α不明显，而σ会产生主导作用，反之亦然.B(t)为标准布朗运动，即E[B(t)]=0，且Var[B(t)]=1[14].

（4）该模型中现货市场的单位运价为外生变量，完全受外部市场经济状况支配，而不受铁路运输企业与期权客户的影响.

（5）铁路货运市场收益率标准差和波动率在资产有效期内为定值，且在无套利完备市场中，期权契约市场双方信息是对称的.

（6）按照需求曲线，期权客户的市场期望收益为市场需求D的函数，需求量D与所运输货物的市场售价p一般是负相关的，例如煤炭、粮食等价值低廉的商品往往对铁路运输存在大量的运输需求，因此，假设需求D=a-bp+ε，ε是分布函数为F(x)，密度函数为f(x)的随机分布[13].

3 模型建立

3.1 三叉树模型说明

原始的三叉树模型从二叉树模型扩展推导而来，虽然二叉树模型有效简化价格变化情况，便于计算，但它只粗略考虑上升和下降两种情况，所以经过n步之后只有n+1种情况.在大多数情况下这种结果并不能满足对于精度的要求.三叉树在模型中增加了一种新的情况，就是经过一段时间后价格不发生变化.使用三叉树更能贴近现实，在这种假设下，经过n步会得到2n+1种结果，使得精度得到提高.

同时，单期的三叉树模型针对时间较长的货运期权，在价值评估上具有局限性，因此本文拟将到期时间分割成多部分，运用多期三叉树模型进行分析，可使期权价值更接近实际.基本三叉树模型如图2所示.

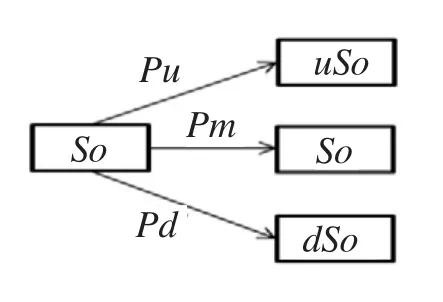
图2 基本三叉树模型Fig.2 Basic trigeminal tree model

3.2 相关期权模型参数求解

单期模型对于时间很短的货运期权来说是可接受的，若如本文所设计的1月的期权，需将到期时间分割成多部分，使期权价值更接近实际.然而随着期数的增加，其价值评估所依赖的相关参数度量就变得复杂，因此，本节利用布朗运动马氏性、鞅性、正态性、二次变差等特性，运用伊藤原理设计求解相关参数.

从原理上看，多期模型是基于单期模型，逐级推进若干层.因此将时间[0,T]按期数分为n等份，则在时间[ti,ti+Δt]内，根据假设（3）可知，标的资产价格服从几何布朗运动，有利用伊藤积分得

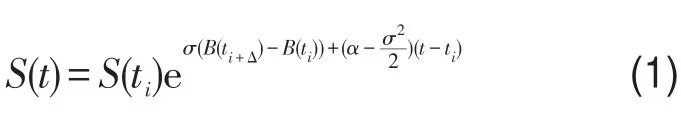
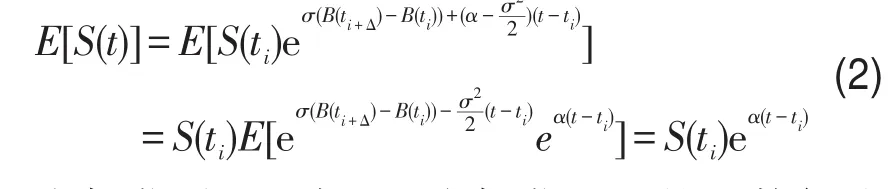
由伊藤引理可知，一个伊藤过程的函数仍然是一个伊藤过程，所以在连续状态下有

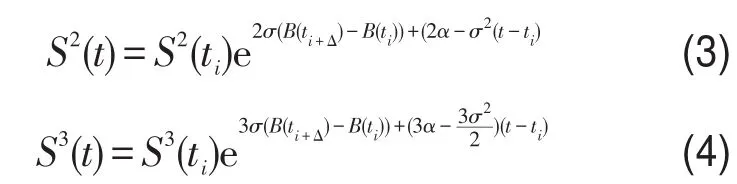
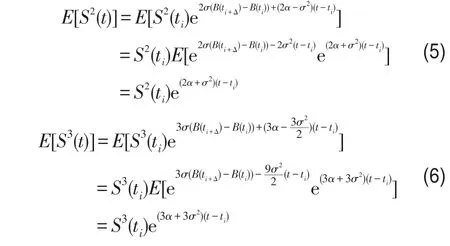
假设在时间段内，运输价格变化有三种状态（见图2），即概率pu,pm,pd分别所代表的现货市场运输价格预期变化的上涨、维持及下跌状态，则应有pu+pd+pm=1.根据式（1）-式（6），可建立pu,pm,pd,u和d的方程组如下：

3.3 期权执行价格及期权购买量的确定

对期权客户的最优期权购买量，以及铁路运输企业最优期权执行价格的确定均需分情况讨论.

情况1当t=T时，若现货市场的运价低于期权执行价格，则期权客户选择直接从现货市场购买，放弃使用期权.

期权客户的利润函数为

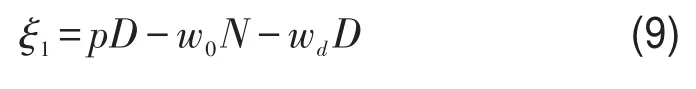
铁路运输企业的利润函数为

则相应的期望利润值分别为

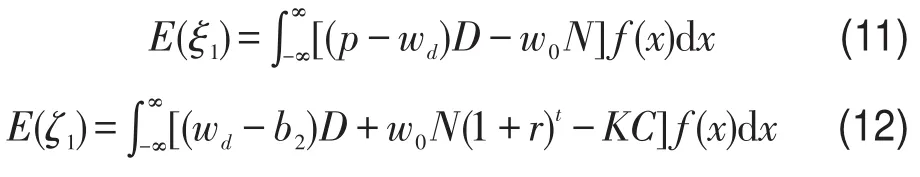
情况2当t=T时，若现货市场的运价不低于期权执行价格，则期权客户的最优决策为行使期权，行使量依货运需求量而定，若货运需求量D高于期权订购量N，则剩余缺口通过现货市场的运力购买获得.

期权客户的利润函数为

铁路运输企业的利润函数为

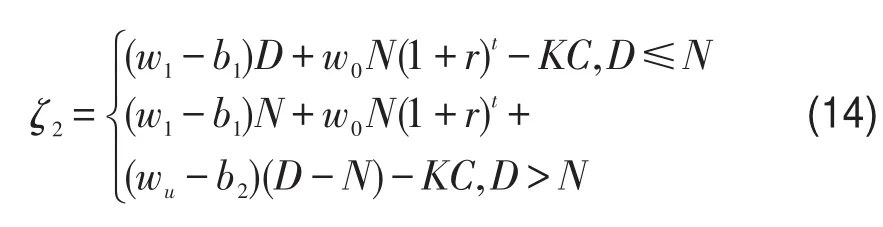
根据假设条件（6），得到相应的期望利润值为

结合两种期望，期权客户和运输企业的期望利润值可分别表示为

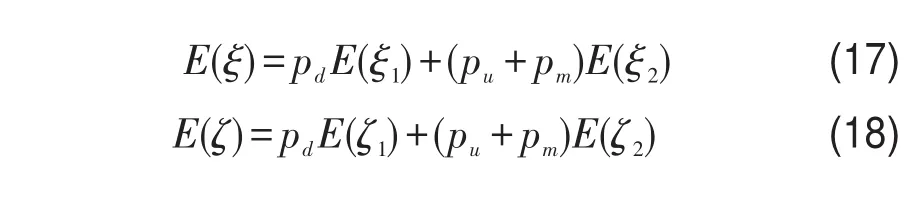
对式（17）和式（18）求N的一阶导数得

由式（19）可得到期权客户的最优期权购买量满足如下条件：

同样，通过求解式（19）和式（20）联立的方程组可得到最优期权执行价格如下：

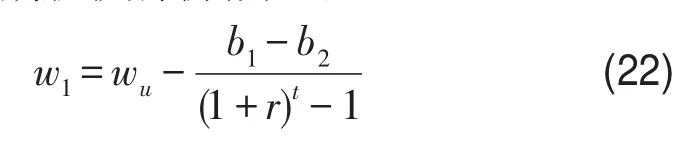
4 算例分析

如图1所示，假设铁路货运市场提前1个月拟定期权价格与期权执行价格，期权客户根据其定价政策选择其最优期权订购量，在现货市场中根据现货市场价格决定期权执行量.假设在期权到期日现货市场的需求函数中，参数ε的分布为[-100,100]的均匀分布，则相应的分布函数可表示为

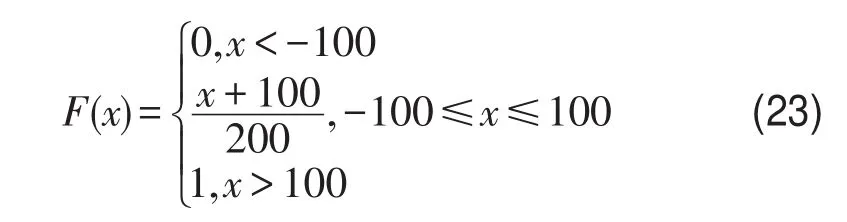
以发货车站大同至到货车站秦皇岛，全长644 km的大秦铁路整车煤炭运输为例.根据原铁道部规定，煤炭按4号运价执行，其发到基价为13.8（元/吨），运行基价为0.0753（元/吨公里），同时参考《铁路货物运价规则》附录一、二、三规定，分别计算货物的铁路建设基金费用0.033（元/吨公里）、电气化附加费0.012（元/吨公里）、新路新价均摊运费0.011（元/吨公里），因为此三项均为提供一定运力必须花费的可能最低成本，故而，取长期准备成本为该三项之和，即b1=0.056，运行基价其余部分可视为短期准备成本，即b2=0.019 3.市场无风险利率r=3.25%，以单期三叉树模型为例，取现行运价标准为期权制定前一天现货市场运力价格S0=62.293 2（元/吨），市场收益率标准差α=0.4，则上行乘数u=1.121 9，下行乘数d=0.891 4.

目前我国政府仍未完全放松对铁路货运价格的管制，虽然运价改革是趋势，但难以一步到位实现运价的完全市场波动.因此，一方面为了便于计算，另一方面为了贴合我国货运现状，预期政府在短时间内，通过调控手段允许运价变动的概率较小，在此施加一个强假设

（当运价改革后完全实现市场化，可删除此假设），代入式（8），重新计算，容易得到：上行概率pu=0.157 6，下行概率为pd=0.175 7，则在单期三叉树模型中，wu=69.886 7（元/吨）.

据此，根据式（22）可看出，最优期权执行价格大小与现货市场运价、长（短）期准备成本、无风险利率相关，从而求得最优期权执行价格w1=58.765 5.为了使求得的期权价格更贴近现实，运用DerivaGem软件对三期三叉树模型求解，得到期权价格w0=3.572 5，如图3所示.

根据式（23）可看出，最优期权订购量与现货市场运价、期权价格、期权执行价格及现货价格上升概率相关.假定D=a-bp+ε中，a=400，b=0.5，p=100，结合相关条件代入式（21），可得期权客户最优期权订购量N=377.综上所述，可得铁路运输企业的最优定价策略：w0=3.572 5，w1=58.765 5.期权客户的最优期权购买量N=377.

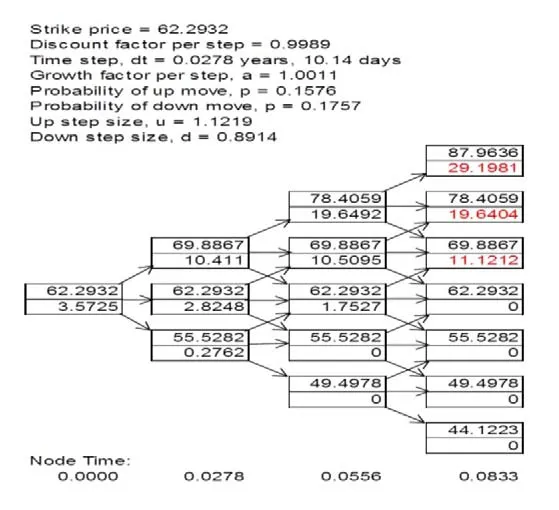
图3 三期三叉树求解过程Fig.3 The third-period trigeminal tree solving process

根据上述假定和结论，计算在铁路运输企业制定不同的价格策略下期权客户的最优期权订购量如表1所示.

表1 不同的价格策略下期权客户的最优期权订购量Table 1 The optimum option order under the different pricing strategies

并针对最优期权订购量对定价政策进行敏感性分析，如图4所示.

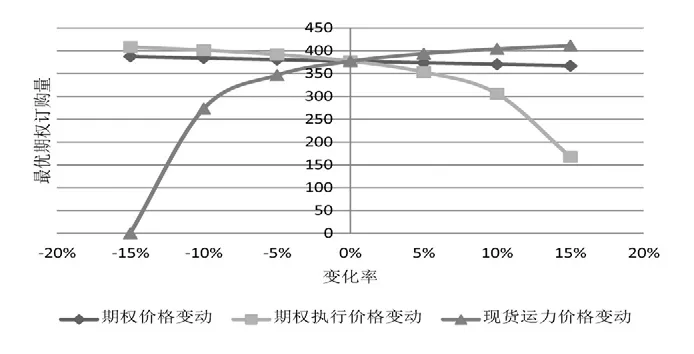
图4 最优期权订购量对定价策略的敏感性分析Fig.4 Sensitivity analysis of the optimal quantity to pricing policy

从表1和图4可以看出：期权客户的期权购买量与期权执行价格及期权价格呈现负相关，相比于期权价格而言，最优期权订购量对期权执行价格具有更高的敏感性，并且当期权执行价格升高幅度超过10%时，期权客户的期权购买量下降梯度迅速增加，其敏感性表现尤为突出.而期权客户的期权购买量与现货市场运力价格呈现正相关，随着现货市场运价的升高，期权客户的期权购买量逐渐增加，当现货市场运价下降幅度超过5%时，期权客户迅速减少期权购买量，并且在降价幅度达到15%时，期权客户会彻底放弃期权购买量.这是因为，只有当期权执行价格小于现货市场价格之时，期权客户才会选择执行期权，反之，期权客户将放弃期权的行使权转向现货市场购买运力.

5 研究结论

本文将期权理论特别是实物期权引入铁路货运，构建基于运输企业和期权客户的多期三叉树定价模型，通过对期权客户最优期权购买量的分析，求解铁路运输企业期权市场最优定价策略.经过相关分析提出，最优期权订购量是关于期权执行价格和期权价格的严格单调递减函数.同时，相比于期权价格，期权执行价格的对期权客户的期权执行量具有更强的敏感性，因此铁路运输企业更应关注期权执行价格的制定.而期权执行价格与现货市场运价、长（短）期准备成本、无风险利率相关.

本文模型是基于双方信息对称及均为风险厌恶者，且不存在违约的假设条件下建立的，但市场行为中双方很难达到信息对称，违约事件也时有发生.故后续研究将侧重此方向的最优决策问题.

[1]Pasternack B A.Optimal pricing and return policies for perishable commodities[J].Marketing Science,1985,4 (2):166-176.

[2]Emmons H,Gilbert S M.The role of returns policies in pricing and inventory decisions for catalogue goods[J]. Management Science,1998,44(2):276-283.

[3]Eppen G D,Iyer A V.Backup agreements in fashion buy⁃ing-the value of upstream flexibility[J].Management Science,1997,43(11):1469-1484.

[4]Tsay A.The quantity flexbility contract and suppliercustomer incentives[J].Management Science,1999,45 (10):1339-1358.

[5]Barnes-Schuster D，Bassok Y，Anupindi R.Coordina⁃tion and flexibility in supply contracts with options[J]. Manufacturing&ServicesOperationsManagement, 2002,4(3):171-207.

[6]Feng Cheng,Markus Ettl,Grace Y Lin,et al.Flexible supply contracts via options[P].IBM TJ Watson Re⁃search Center Working Paper.2003,87:92-97.

[7]Wu D J，Kleindorfer P R，Zhang J E.Optimal bidding and contracting strategies for capital-intensive goods [J].European Journal of Operational Research.2002, 137(3):657-676.

[8]Stefan S,Huchzermeier A,Klerndorfer P.Risk hedging via options contracts for physical delivery[J].OR Spec⁃trum,2003,25(3):1-17.

[9]Wang Qun-zhi，Tsao De-bi.Supply contract with bidi⁃rectional options:The buyer’s perspective[J].Interna⁃tional Journal of Production Economics，2006,101(1): 30-52.

[10]Steen Koekebakker,Roar Adland,Sigbjørn Sødal.Pric⁃ing freight rate options[J].Transportation Research Part E,2007,43(5):535-548.

[11]Koichiro Tezuka,Masahiro Ishii,Motokazu Ishizaka.An equilibrium price model of spot and forward shipping freight markets[J].Transportation Research Part E.2012, 48(4):730-742.

[12]Nikos K Nomikos,Ioannis Kyriakou,Nikos C Papaposto⁃lou,et al.Freight options:Price modelling and empirical analysis[J].Transportation Research Part E.2013,51:82-94.

[13]冯芬玲,李菲菲.基于期权理论的铁路货运定价模型[J].铁道科学与工程学报,2012,9(2):72-78.[FENG F L，LI F F.Pricing model of railway cargo transport based on option theory[J].Journal of Railway Science and En⁃gineering.2012,9(2):72-78.]

[14]王晓林,杨招军.基于效用的永久性可转换债券定价[J].管理科学,2013,26(3):100-107.[WANG X L，YANG Z J.Permanent convertible bonds pricing based on utility theory[J].Journal of Management Science. 2013,26(3):100-107.]

Railway Freight Pricing Model Based on Trigeminal Tree

GUO Jing-wei,PENG Qi-yuan
（School of Transportation and Logistics，Southwest Jiaotong Universiy，Chengdu 610031，China）

Introducing the option theory into railway freight pricing activities,this paper establishes a multi-phase trigeminal tree pricing model to maximize the expectation of transportation enterprise and contract customers.It then analyzes the optimal pricing decision of the railway transportation enterprise and compares customers’optimal purchase decisions.The results show that:the optimal ordering quantity of option is a strictly monotone decreasing function to option price and exercise price.A positive correlation is identified between strike price and spot market freight,short-term preparation cost,as well as risk-free interest rate;the correlation between strike price and long-term preparation cost is negative.The case study illustrates that the option purchases will get a rapid reduce when the strike price rise more than 10%.Meanwhile,compared to the option price,options strike price has stronger sensitivity to the number of options execution. Thus,the railway transport enterprise should focus on the options exercise price.

rds:transportation economy;option pricing;trigeminal tree model;exercise price;options contract

1009-6744（2014）04-0194-07

F532.5

A

2013-11-06

2014-02-24录用日期：2014-02-26

铁道部科技研究开发计划（2014X009-K）.

郭经纬（1986-），男，河南洛阳人，博士生. *

qiyuan-peng@home.swjtu.edu.cn