基于速度里程分布的快速路宏观交通状态评价模型

岳园圆，于雷*,2，朱琳，宋国华，陈旭梅

（1.北京交通大学交通运输学院，北京100044；2.德克萨斯南方大学交通系，美国休斯顿77004；3.上海工程技术大学城市轨道交通学院，上海201620）

基于速度里程分布的快速路宏观交通状态评价模型

岳园圆1，于雷*1,2，朱琳3，宋国华1，陈旭梅1

（1.北京交通大学交通运输学院，北京100044；2.德克萨斯南方大学交通系，美国休斯顿77004；3.上海工程技术大学城市轨道交通学院，上海201620）

随着城市规模的不断扩大，快速路已成为支撑城市道路交通系统运行的重要部分.准确的快速路宏观交通状态评价是快速路交通管理的关键.本文以北京市西三环为例，引入交通流宏观基本图模型，设计了基于速度里程分布的快速路宏观交通状态指数（MTCI）.首先，利用RTMS数据，建立了宏观基本图模型.在此基础上，将快速路宏观交通状态划分为畅通、基本畅通、轻度拥堵、中度拥堵和阻塞五个等级.然后，利用浮动车数据建立了快速路车辆运行速度累积里程分布模型.通过关联宏观交通流状态与车辆运行速度累积里程分布，构造了基于速度里程分布的MTCI评价方法，并通过实例验证了该模型的适用性.

城市交通；宏观交通状态指数；宏观基本图；快速路；车辆运行速度累积里程分布

1 引言

随着北京的快速发展与城市的不断扩张，快速路系统已成为支撑城市交通的重要部分.为了检测快速路的运行特征，北京环路上已安装了上百个RTMS检测器，且全市路网上有6万多辆浮动车，可以实时收集大量的交通运行数据.基于现有的RTMS数据和浮动车数据进行快速路宏观交通状态评价，可为交通管理者提供直观准确的快速路交通运行信息，便于设计和实施交通管理措施和控制方案.

迄今为止，很多宏观交通状态评价模型和评价指标被提出.Herman等[1]提出二流理论，并将其用于描述城市交通网络中集中流特征.王殿海等[2]运用二流理论推导路网宏观交通参数之间的函数关系，建立路网宏观交通状态判别模型.在以道路网络为研究对象时，基于二流理论的交通运行效果评价具有良好的应用效果.但是，其单纯地将路网中的车辆分为运动车辆和停止车辆的基本思想，不能用于指导交通管理和交通出行；且复杂的参数设置限制了其应用.Daganzo等[3]在前人研究的基础上，发现了路网上流量、速度和密度等基本交通流参数之间的定量关系，并将此定义为宏观基本图（Macroscopic Fundamental Diagram,MFD）. Yang等[4]基于仿真数据研究了宏观基本图的形状；Nikolas Geroliminis等[5,6]基于美国旧金山、日本横滨等城市路网的交通数据总结了数种路网MFD模型结构；Cassidy等[7]曾采用矢量算法集成得到多个检测点的宏观交通流参数模型.可见，已有研究多关注于模型的形式和存在条件，有必要进一步探究宏观基本图模型与宏观交通状态之间的关系.

交通流基本参数（包括流量、密度和速度）始终是研究道路交通特性的重要指标；同时，基于大量统计数据的综合性指标陆续被提出.其中值得一提的是北京市现行使用的“交通运行指数”（TPI）[8]，它是将特定区域特定时刻的单个路段、某等级道路或整体路网的拥堵强度量化后的相对数，其取值为[0,10]的实数，分别对应“畅通”、“基本畅通”、“轻度拥堵”、“中度拥堵”、“严重拥堵”五种状态.路网层面的TPI以路段严重拥堵里程比例、各等级道路的车辆行驶里程（VMT）比例为基础计算得到，而对路段拥堵程度判别的速度标准来自于交通参与者拥堵感知调研[9].TPI能够直观、实时地表示交通状态，在国内得到广泛关注.但是，该指标只考虑了严重拥堵里程比例，能否准确代表道路上大部分车辆的运行状况还有待验证.

在以上研究的基础上，本文以北京市西三环为例，将交通流宏观基本图理论引入北京市快速路宏观交通问题的研究中，设计基于速度里程分布的快速路宏观交通状态指数（MTCI）的计算方法，并通过实例分析该模型的适用性.

2 模型建立

本文提出的模型由三部分组成：

（1）利用RTMS数据建立宏观基本图模型，并对快速路宏观交通状态进行多级划分，提出宏观交通状态指数（MTCI）；

（2）利用浮动车数据建立不同宏观交通状态下车辆运行速度累积里程分布模型，并选取百分位速度作为对应状态等级的速度阈值；

（3）通过关联宏观状态等级和速度阈值构造了快速路宏观交通状态指数的求解公式.其研究框架如图1所示.

2.1 基于宏观基本图的快速路宏观交通状态多级划分

交通流基本图模型，通常被用于描述单个断面或路段的交通流行为特征.而MFD模型，是从路网整体结构出发，分析道路多个断面或区域路网多条道路的空间平均交通流变量之间的关系.本文借鉴参考文献[7]提出的矢量算法，利用2006年3月16日-18日北京西三环RTMS提供的20个被检测路段的流量、占有率和速度数据，获得该路网平均流量—平均密度、平均流量—平均速度和平均密度—平均速度关系散点图.然后，基于Van Aerde模型标定交通流宏观基本图的特征参数（路网平均自由流速度FS、通行能力下的速度SC、通行能力CAP和阻塞密度JD），最终得到西三环快速路的宏观基本图模型[10]，如图2所示.

与TPI不同，本文利用宏观基本图模型对快速路的宏观交通流状态进行等级划分.参考拥堵感知调研[9]的速度阈值划分结果，并根据宏观基本图中散点分布位置，将快速路的宏观交通流状态划分为Ⅰ～Ⅴ五个等级，对应等级的参数阈值如图2所示.为更好地量化快速路宏观交通流状态，提出定量的评价指标——“宏观交通状态指数（MTCI）”，并借鉴TPI的量化方法采用[0,10]的连续实数表示快速路“宏观交通状态指数”的评价结果.

图1 快速路宏观交通状态评价模型建模思路Fig.1 Outline of the expressway macroscopic traffic condition evaluation modeling

五种等级下的宏观交通流状态特征：

(1)Ⅰ级-畅通：交通流整体为自由流状态，样本点落在低密度、低流量区间，车辆在路网内行驶不受外界干扰.

(2)Ⅱ级-基本畅通：样本点同样分布在低密度、低流量区间，快速路上大部分路段交通运行畅通或接近自由流状态，存在少量路段交通流状态不稳定，但不会形成拥堵或长时间排队.

(3)Ⅲ级-轻度拥堵：平均流量接近通行能力，但平均密度低于临界密度.此时，快速路上大部分路段密度低于或接近临界密度，若交通需求继续增加，平均流量会逐渐下降.

(4)Ⅳ级-中度拥堵：平均密度已经超过临界密度，平均流量开始从通行能力处下降.此时，快速路各路段交通流状态差异开始增大，道路上的车流排队情况开始恶化，但快速路整体状态仍可控.

(5)Ⅴ级-严重拥堵或阻塞：数据样本点集中分布在高密度、低流量区间.快速路已经出现大范围拥堵，大部分路段已处于阻塞流状态.

2.2 不同宏观交通状态下的速度累积里程分布模型

为了研究路网内车流状态的分布特征，本部分采用与TPI一样的数据基础——浮动车数据，建立快速路车辆运行速度里程分布模型.与RTMS数据相比，浮动车数据覆盖范围广，能反映道路上绝大部分车辆的运行状况.

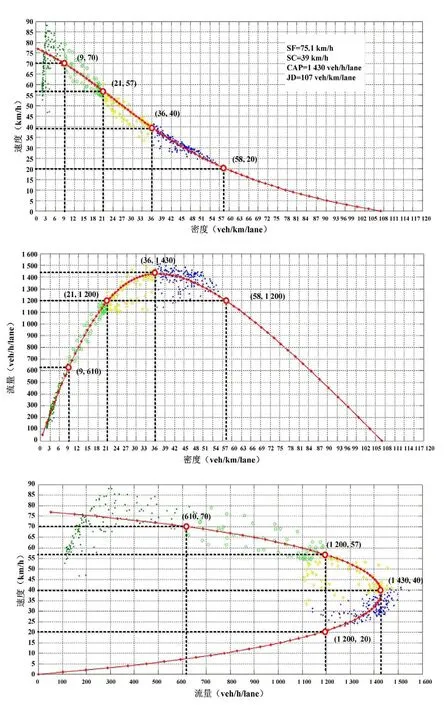
图2 西三环快速路宏观交通流状态等级划分Fig.2 Five levels of macroscopic traffic condition classified for the western 3rd ring-road expressway

在任意一个时间间隔内，若某路段的浮动车平均速度为vi，对应单位里程行程时间为ti，二者满足ti=1vi.设一个时间间隔内，平均速度为vi（或单位里程行驶时间为ti）的路段共有m条，则平均速度为vi所对应的车辆行驶里程比例为

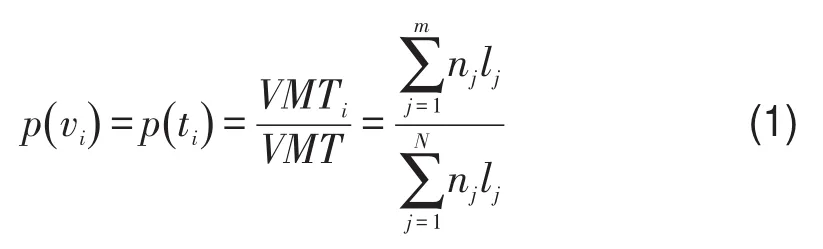
式中nj为路段j上运行车辆数；lj为路段j的长度；N为路段总数量.

假设快速路上所有路段的车流量均相等，即nj为固定值，则式（1）可进一步转化为

由此，可得到快速路上速度值vi的里程比例p(vi)的分布情况，转化为运行速度v的里程分布概率密度函数f(v)或对应单位里程行程时间t的里程分布概率密度函数为f(t).根据t=1/v，求解快速路运行速度v和单位里程行程时间t的里程比例的累积概率分布函数关系为

利用某工作日北京市西三环快速路5 min间隔浮动车数据，任意选取了高峰8:25和平峰10:25两个时刻，统计快速路各路段的单位里程行驶时间，并按照式（2）计算单位里程行程时间的里程比例.分别采用Normal、Lognormal、Gamma和Weibull四种常用分布进行曲线拟合（如图3所示），确定了快速路上车辆单位里程行程时间的里程比例分布服从对数正态分布函数，由式（4）给出：

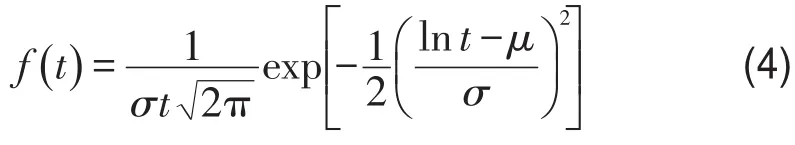
式中t表示分析时段的车辆单位里程行程时间；μ和σ分别为快速路单位里程行程时间概率分布模型的平均值和方差，满足t＞0，σ＞0，-∞＜μ＜+∞.

图3 单位里程行程时间概率分布图Fig.3 Probability distribution charts of unit travel time for two time periods

对于任意时间，μ和σ可以通过对所有车流单位里程行程时间的对数进行统计计算获得，分别为lnt的期望值和标准差，计算公式为

式中ti为第i个单位里程行程时间取值；xi表示单位里程行程时间ti的对数；n表示研究时段快速路上单位里程行程时间的取值个数；x¯和SD() x分别表示研究时段内单位里程行程时间的对数的均值和标准差.

在给出单位里程行程时间的里程分布的概率密度函数之后，累积概率分布函数可以表示为

根据式（3），快速路上的车辆运行速度的累积里程概率分布模型为

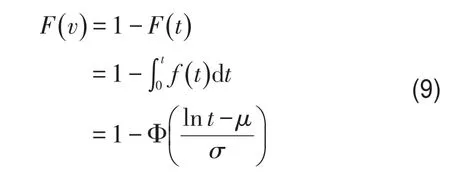
针对所得到的2006年3月16日-18日西三环快速路宏观交通流状态（如图2所示），计算每个10分钟间隔的车辆运行速度累积里程概率分布，3天共得到432条概率分布曲线（不同的灰度表示不同的状态等级），如图4所示.其中，横坐标表示车辆运行速度，且取值由高向低，对应单位里程行程时间由0向∞；纵坐标为运行速度的累积概率.图中不同灰度的线条落在坐标系的不同区域，这说明当快速路宏观交通流状态不同时，车辆运行速度的里程分布也不同.

图4 基于速度分布的宏观交通状态等级对应速度阈值划分Fig.4 Dividing method of speed threshold values corresponding to five macroscopic traffic condition levels based on speed distributions

2.3 基于速度分布的宏观交通状态指数评价方法

设曲线上的任一点的纵坐标取值为F(vi)，表示快速路上以小于（含）速度vi所完成的车辆行驶里程的总比例.定义F(vi)=15%为临界点，将其对应的速度值vi作为评价快速路宏观交通流状态的自变量，即该时间段内的车辆行驶里程中有85%的运行速度不低于vi.将vi作为评价快速路宏观交通状态的自变量，不同状态等级对应的速度阈值如图4所示.采用线性方程式表达基于速度分布的快速路宏观交通状态指数（MTCI）评价方法，如式（10），其中v表示累积里程比例为F(vi)=15%所对应的速度值.考虑西三环限速80 km/h，因此，当F(vi)=15%所对应速度值为80 km/h时，直接定义宏观交通流状态为Ⅰ级，MTCI=0.

3 应用示例

3.1 方案设计

以西三环快速路为例，利用2007年4月4日的浮动车数据，采用TPI和MTCI两种指数评价西三环宏观交通流状态，并对比评价结果.

评价方法一：以10 min为间隔，根据《城市道路交通运行评价指标体系》中关于TPI的计算步骤，计算每个时间间隔西三环快速路的TPI.

评价方法二：以10 min为间隔，统计西三环快速路上的车辆运行速度的里程分布比例，获取累积里程比例F(vi)=15%所对应的速度值，并根据式（10）计算每个时间间隔的MTCI.

3.2 结果分析

针对西三环快速路交通流状态，两种指标的评价结果，如图5所示，

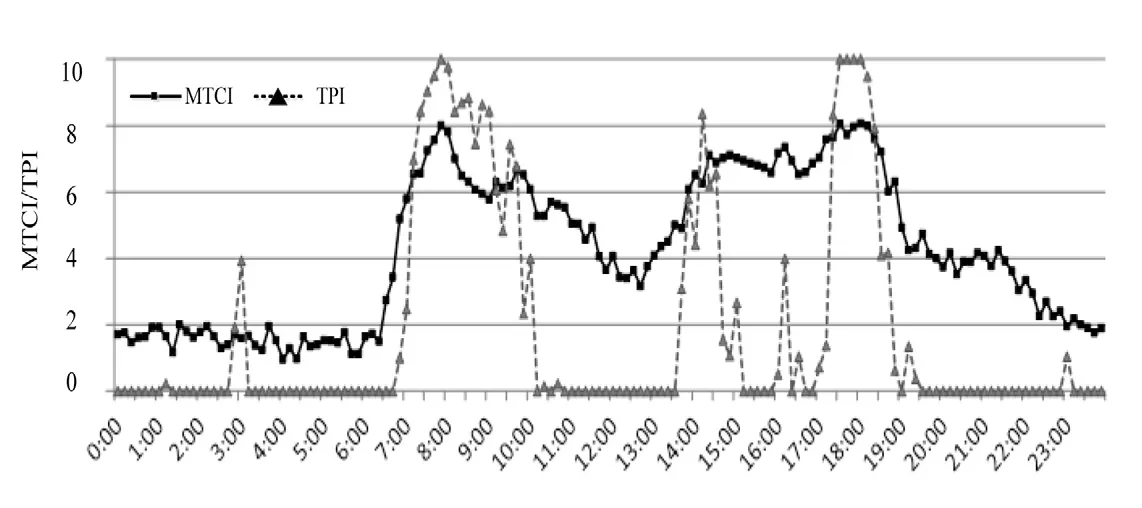
图5 西三环快速路宏观交通状态评价结果对比Fig.5 Comparisons of evaluation results of the macroscopic traffic condition on western 3rd ring-road expressway

经计算，MTCI与TPI的等级划分吻合度超过85%，验证了模型的有效性.另外，由于综合考虑了道路上绝大部分车辆的运行状况，MTCI曲线在呈现一天不同时段快速路整体交通状态时不会出现骤增或骤减的现象；而TPI只考虑了道路上严重拥堵的范围，曲线波动过于剧烈.具体表现为：在夜间或午间的交通平峰时段，快速路上未发生或极少路段发生严重拥堵时，道路交通运行指数会骤减为0，而当平峰时段道路上发生微小交通意外或波动时，TPI的计算结果又会急剧上升.综上分析，对于单一等级的快速路，本文所提出的基于速度分布的MTCI指标具有更好的适应性.

4 研究结论

本文以“建立快速路宏观交通状态评价模型”为目标，构建了基于车辆速度累积里程分布的MTCI评价方法.在模型建立过程中，（1）基于RTMS数据，结合交通流宏观基本图理论，将快速路宏观交通状态划分为畅通、基本畅通、轻度拥堵、中度拥堵和严重拥堵五个等级；（2）基于浮动车数据，建立了车辆运行速度的累积里程概率分布模型，并得出快速路上车辆运行速度累积里程分布服从对数正态分布.最后，采用MTCI和TPI分别对同一天西三环的交通状态进行宏观评价，结果表明：对于单一等级的快速路，综合考虑了大部分交通运行状况的MTCI具有更好的适应性.

本研究设计的基于速度空间分布的快速路宏观交通状态评价模型的研究思路，可以实现快速路短时交通状态评价，对交通管理和交通出行具有指导意义.尽管研究中引入了宏观基本图模型，但模型结构、路网规模均较简单，后续将进一步扩大路网研究范围，并将尝试基于浮动车数据建立快速路宏观基本图.

[1]Herman R，Prigogine I.A two-fluid approach to town traffic[J].Science,1979,204:148-151.

[2]王殿海,陈松,魏强,等.基于二流理论的路网宏观交通状态判别模型[J].东南大学学报（自然科学版）, 2011,41(5):1098-1103.[WANG D H,CHEN S,WEI Q,et al.Discrimination model for macroscopic traffic conditions of urban networks using two-fluid theory[J]. Journal of Southeast University:Natural Science Edi⁃tion,2011,41(5):1098-1103.]

[3]Daganzo C F，Geroliminis N.An analytical approxima⁃tion for the macroscopic fundamental diagram of urban traffic[J].Transportation Research Part B:Methodologi⁃cal,2008,42(9):771-781.

[4]Ji Y,Daamen W,Hoogendoorn S,et al.Investigating the shape of the macroscopic fundamental diagram using simulation data[J].Transportation Research Record: Journal of the Transportation Research Board,2010, 2161(1):40-48.

[5]Geroliminis N，Sun J.Hysteresis phenomena of a macro⁃ scopic fundamental diagram in freeway networks[J].Pro⁃cedia-Social and Behavioral Sciences,2011,17:213-228.

[6]Geroliminis N，Sun J.Properties of a well-defined macro⁃scopic fundamental diagram for urban traffic[J].Trans⁃portation Research Part B:Methodological，2011,45(3): 605-617.

[7]Cassidy M J,Jang K,Daganzo C F.Macroscopic funda⁃mental diagram for freeway network:theory and observa⁃tion[D].90thTransportation Rsearch Board Annual Meeting CD-ROM,#11-0657.Washington D C,US, 2011.

[8]北京交通发展研究中心.DB11/T785-2011城市道路交通运行评价指标体系[S].北京市质量技术监督局, 2011.[Beijing Transportation Research Center.Urban road traffic performance index[S].Beijing Municipal Administration of Quality and Technology Supervision, 2011.]

[9]交通拥堵评价研究报告(k06006)[R].北京:北京交通发展研究中心,北京四通智能交通系统集成有限责任公司,北京交通大学交通规划与管理长江学者研究中心,2007,9.[Research report for congestion evaluat⁃ing k06006[R].Beijing:Beijing Transportation Re⁃search Center,Beijing Jiaotong University Chang Jiang Scholars Research Center,2007,9.]

[10]朱琳.城市快速路交通态势评估理论与方法研究[D].北京：北京交通大学,2013.[ZHU L.Theory and meth⁃od studies on traffic situation assessment for urban ex⁃pressways[D].Beijing:Beijing Jiaotong University, 2013.]

Macroscopic Model for Evaluating Traffic Conditions on the Expressway Based on Speed-Specific VKT Distributions

YUE Yuan-yuan1,YU Lei1,2,ZHU Lin3,SONG Guo-hua1,CHEN Xu-mei1
(1.School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China; 2.College of Science and Technology,Texas Southern University,Houston TX 77004,America; 3.College of Urban Railway Transportation,Shanghai University of Engineering Science，Shanghai 201620,China)

ract:With the continuous expansion of urban land,expressways have become key factors that support the entire urban road traffic operation.Accurate evaluation of traffic condition is the key of traffic management.This paper introduces the macroscopic fundamental diagram model and develops macroscopic traffic condition index(MTCI)based on speed-specific vehicle kilometers traveled(VKT)distributions by taking western 3rd ring-road expressway as an example.First,a macroscopic fundamental diagram model is established based on the RTMS data.Macroscopic traffic conditions on the expressway are classified into five levels(free-flow,near-free-flow,light congestion,moderate congestion,and severe congestion)based on the macroscopic fundamental diagram model.Subsequently,the speed spatial distribution model is designed using the floating car data.Furthermore,associating macroscopic traffic conditions with the cumulative distribution of travel speeds on the expressway,this study develops the MTCI evaluation method based on speedspecific VKT distributions.Finally,the proposed model is tested and verified using the western 3rd ring-road expressways.

rds:urban traffic;macroscopic traffic conditions index;macroscopic fundamental diagram;expressway;cumulative distribution of travel speeds

1009-6744（2014）04-0085-08

U491.1

A

2013-11-08

2014-02-25录用日期：2014-03-10

国家“973”计划项目（2012CB725403）；新世纪优秀人才支持计划（NCET-12-0763）；北京交通大学基本科研业务费（T14JB00180）.

岳园圆（1989-），女，山东聊城人，硕士生. *

yu_lx@tsu.edu