超大型耙吸挖泥船的自由振动分析
孙雪荣 乔国瑞
(中国船舶及海洋工程设计研究院 上海 200011)
超大型耙吸挖泥船的自由振动分析
孙雪荣 乔国瑞
(中国船舶及海洋工程设计研究院 上海 200011)
采用直接简化计算方法和三维有限元方法对某超大型耙吸挖泥船进行自由振动频率的计算。直接简化计算方法参考CCS船体梁固有频率计算;三维有限元方法借助商用有限元软件,建立全船三维有限元模型,结合初期的总体质量分布,进行直接计算。论文旨在寻求适合于挖泥船类的船体梁固有频率估算方法,以及探讨随着船舶大型化和高强度钢的大量使用而可能引发的超大型耙吸挖泥船的船体波激振动问题。
自由振动;有效质量;有效刚度;波激振动
引 言
舱容在8 000 m3以上的大型耙吸船最早出现于20世纪60年代的后期。1994年,第一艘17 000 m3超大型耙吸挖泥船的诞生,标志着耙吸挖泥船已朝着超大型化发展。随着耙吸挖泥船的大型化以及高强度钢的普遍使用,随之而来的船舶总体性能、刚度与强度等问题也就成为研发设计的重要课题。
本文以我院自主研究开发的38 000 m3耙吸挖泥船为基础,以直接简化计算和有限元方法进行船体梁1阶和2阶垂向自由振动的预报,旨在通过借助CCS船体梁振动估算方法[1-2],结合三维有限元计算,寻求适用于挖泥船类便捷有效的工程实用方法,并探讨随着船舶大型化而引起的弯曲刚度较低可能导致的波激振动问题。
1 计算模型简介
论文中的计算模型取挖泥船满载状态,满载排水量为94 691 t。图1为该船总布置图,基本参数见表1。

图1 总布置图

表1 基本参数m
2 船体梁固有频率估算
2.1 三维有限元计算
38 000 m3超大型耙吸挖泥船的自由振动有限元计算借助大型商用有限元软件MSC/PATRAN 、MSC/NASTRAN完成,
以强框架为单元间距,以三维实体弱弹性单元模拟泥舱装载质量,建立满载状态下的有限元计算模型(见图2)。
在船体质量调整中,船体自身质量的调整通过调节单元结构的材料密度和施加典型结构质量点来实现;不同装载状态的载重量通过在相应装载位置的结构单元附近施加典型结构质量点以及泥舱内建立三维实体弱弹性单元来实现(即三维弱弹性单元不参与船体梁刚度计算);船体附连水振动质量在MSC/NASTRAN内通过定义有限元模型湿表面单元和吃水高度实现自动计算。

图2 三维有限元模型示意图
有限元计算所得的船体梁自由振动频率参见表2,下页图3 -图6为典型的振型示意图。由有限元计算结果可知,单纯的水平振动并没有搜索到,水平振型大多与扭转振型耦合,2阶垂向振动与1阶扭转振动的频率非常接近。
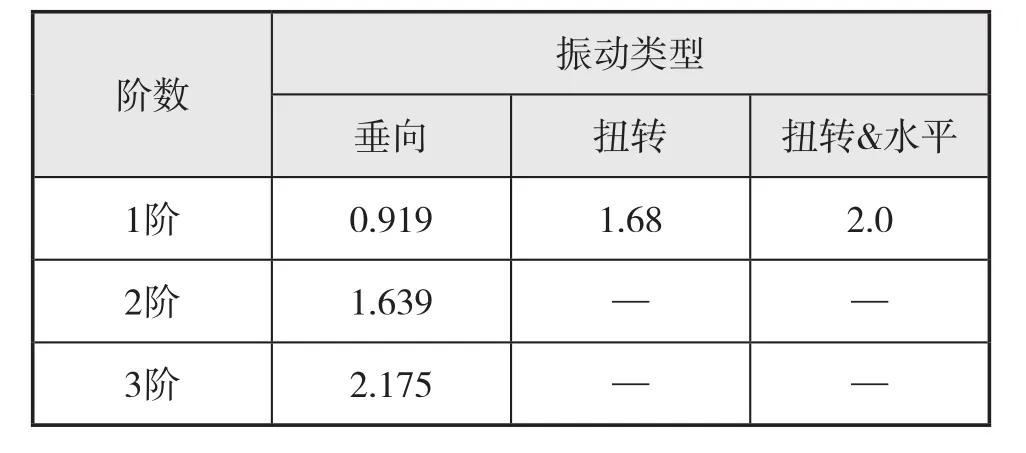
表2 自由振动结果Hz

图3 主要振型示意图(1阶垂向)
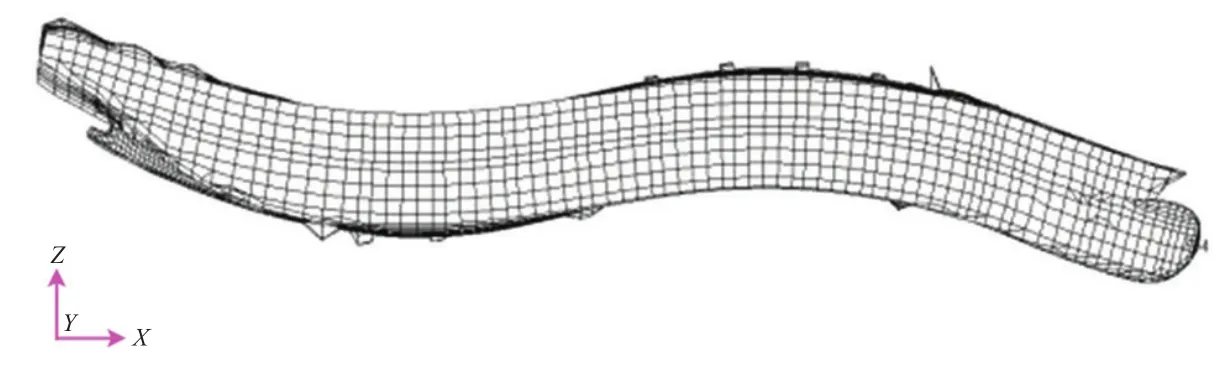
图4 主要振型示意图(2阶垂向)
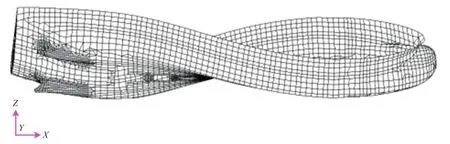
图5 主要振型示意图(1阶扭转)

图6 主要振型示意图(3阶垂向)
满载状态的1阶垂向振动频率为0.919 Hz。随着挖泥船日趋超大型化,船体梁固有频率已减小到1.0 Hz以下。结合文献[3]所记载的同尺度干货船和散货船实船的波激振动频率0.8~1.06 Hz之间[3],本文随后将对波激振动作进一步讨论。
2.2 直接简化计算
自由振动直接简化计算方法借助CCS船体梁固有频率估算方法完成,该方法是根据100余艘不同类型船舶的资料予以归纳,适用于船长小于230 m的油船、干货船、散装货船、矿砂船和客货船,一般情况下的误差不大于7%[1]。
本文的研究对象为耙吸挖泥船,虽然表面上并不适用于CCS直接简化方法,但由于泥浆的特殊性,耙吸挖泥船与油船、散货船和矿砂船的货物相似。本文采用CCS方法直接简化计算旨在借助CCS船体梁固有频率估算方法,对与本文所研究的挖泥船同尺度的油船、散货船和矿砂船的固有频率估算,并与三维有限元方法得到的本挖泥船的固有频率进行比较,探讨适合挖泥船的固有频率估算公式,供类似挖泥船在固有频率估算方面参考,从而提高工作效率。
当主尺度和排水量已知时,船体梁垂向弯曲振动的第1阶和第2阶固有频率可按式(1)计算[1]:

式中:i为船体梁垂向弯曲振动的节点数,第1阶取i=2,第2阶取i=3;fiv为节点数为i的船体梁垂向总振动的固有频率,Hz;D为型深,m,由基线量至强力甲板的高度;L为垂线间长,m,公式适用范围L≤230 m;B为型宽,m;aiv与biv为根据船的类型和节点数确定的无因次系数;Kiv为船体横剖面对中和轴的惯性矩沿船长分布形式的变化,对固有频率影响的无因次修正系数;Eiv为船体桥楼对固有频率影响的无因次修正系数;为包括附连水质量在内的船舶总质量,t;Civ为船体钢材类型对船体振动影响的系数。
2.2.1 aiv、biv由表3确定
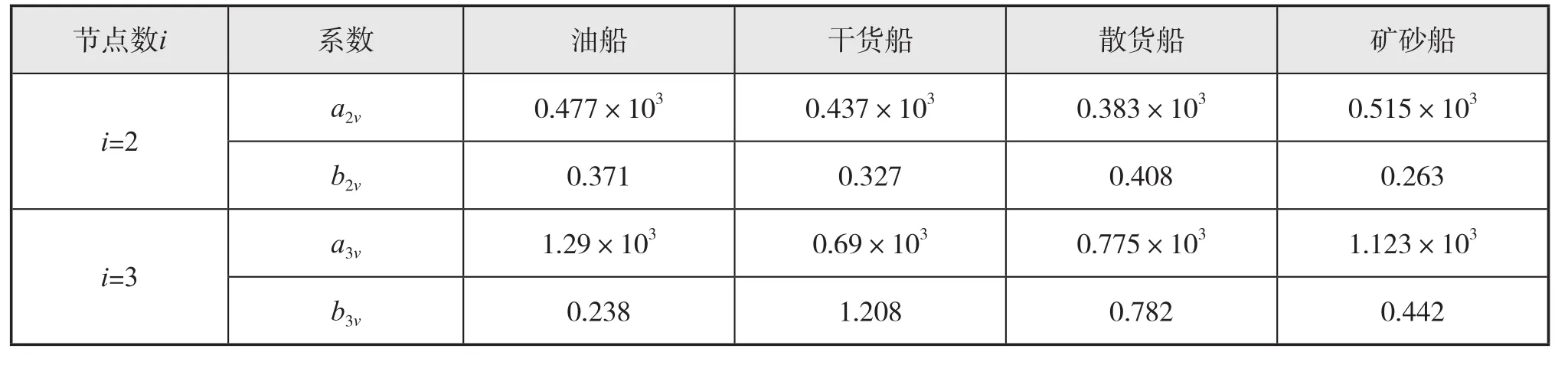
表3 系数aiv、biv
2.2.2 Kiv由式(2)、式(3)确定
式中: Cb为方型系数。
2.2.3 Eiv由式(4)、式(5)确定
式中:De为相当型深,m;由式(6)确定。

式中:L1、D1、L2、D2、L3、D3分别是各层桥楼长度及由船底至该层桥楼的对应高度,见图7。
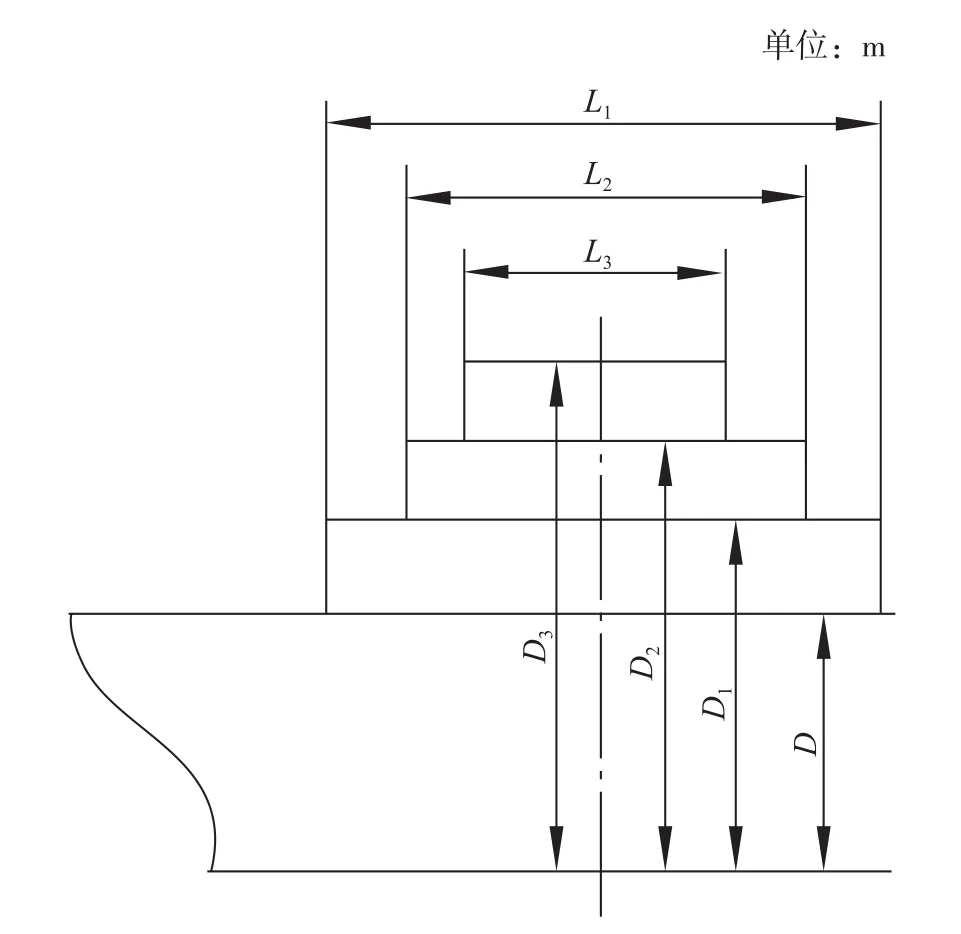
图7 型深和桥楼尺寸示意图
式(6)中的k是不同种类桥楼的系数。当桥楼为上层建筑时,k=1.0;当桥楼为甲板室时,k=0.95。
x1、x2、x3分别为:



式中:d为平均吃水,m;B为船宽,m;Cb为方型系数。
2.2.5 Cvm
船体采用普通钢材时, Cvm=1.0;当船中部区域内主要船体结构采用高强度钢时,Cvm由式(9)确定。

式中:Km为材料换算系数。
3.日本智能制造系统的目标。日本发起IMS倡议的根本目的在于智能制造技术的创新,IMS涉及的技术领域包括产品全生命周期技术、生产工艺的改善、生产系统软硬件工具的更新、企业管理模式的开发及企业成长发展模式的创新等。为完成其肩负的使命和实现预期的收益,IMS系统确立了十大重点研发领域,包括可持续动力、模拟仿真、定向需求等(林捷,2003)。[10]
由以上公式结合38 000 m3超大型耙吸挖泥船的主要尺度,计算得到四类同尺度运输船满载状态下的自由振动频率(见表4)。有限元计算与直接简化计算所得结果百分比的比较见下页表5。

表4 直接计算频率值Hz

表5 直接计算与有限元计算结果百分比的比较%
通过与本挖泥船同尺度的四种船型直接简化计算结果及与三维有限元计算结果的比较可知,挖泥船类的船体梁振动固有频率估算可借助CCS关于散货船固有频率的估算方法,1阶和2阶垂向振动固有频率估算值与三维有限元计算所得结果相差分别为3.7%和5.3%。
本文没有针对船体梁的水平和扭转振动进行直接简化计算,主要是考虑在38 000 m3超大型耙吸挖泥船的有限元计算结果中,在扭转振型中已开始出现与水平振型的耦合现象,这一点在大型运输船上也有类似现象发生。本文主要开展对船体梁低阶振动固有频率的估算,是因为伴随着船舶大型化而出现的波激振动现象已成为当前大型船舶特有的技术问题。
3 船体梁波激振动
波激振动的明显表现对于船长为180~200 m的较大尺度海船,以及船体型深与长度之比H / L为1/16~1/18(如:有限航区浅吃水船舶,河海混杂航行船舶)这类弯曲刚性较低的船舶是特有的[2]。
波激振动[4-7]现象自20世纪60年代起,从大型矿砂船开始受到关注。船舶尺度的增大,意味着船体弹性增大以及2节点垂向振动频率降低。正如在大吨位油船航海试验中发现的那样,在波浪不高的迎浪情况下(波高为3~5 m),振动应力可与船体在波浪上的普通低频应力比拟;随着波浪强度的增加,观察到振动应力相对减小。前文已指出,首端形状(如球鼻艏)可使振动应力增加一倍,而且船舶相对于波浪运动的航行速度增加具有实质性影响,会导致形成波激振动的船体总纵弯曲共振现象。对于海船,波激振动发生在相对短的波浪情况(λ/L约为0.05~0.20),且其相互作用的水动力理论还没有充分研究[2]。
波激振动对船体梁极限载荷的影响[5]:对一艘250 000 t油船,长期可以增加5%;对一艘超大型集装箱船,短期可使波浪弯矩增加100%,长期可增加3%~5%;对一艘250 000 t矿砂船,短期可使波浪弯矩增加50%。(注:这里所说的“长期”或“短期”是指波浪统计的长短。)
波激振动对挖泥船的长期和短期影响的研究并不多见。文献[4]仅是在宽水域施工中有可能引起的共振分析;文献[3]中对船舶波激振动实船测试结果中列出的均为运输类散货船、油船等,表6引自文献[3]中与本文研究的38 000 m3超大型耙吸挖泥船同尺度的实船测量结果。

表6 船舶波激振动实船测量结果[3]
当某一倍频程频率等于或接近于1阶振动频率时,船体梁将会在没有砰击的情况下产生波激振动,而不一定是遭遇频率等于船体梁1阶振动频率时才会产生波激振动[6]。通常当波浪周期较短且波高较小时,大型船舶容易发生波激振动,但迅即会被船员发现,故可降低航速或改变航向来减小波激振动[3]。波激振动与船舶的主尺度、航速、航向、装载、航线等都有关系,但不可否认的是,船舶尺度的大型化以及波激振动已经成为大型船舶不可避免的典型问题。这不仅影响船舶在海上的航行安全,也增加船体结构的维修成本。
对于超大型耙吸挖泥船,长期引起的疲劳问题、短期引起的波浪弯矩增加以及波激振动,同样是不可避免的技术难题。38 000 m3超大型耙吸挖泥船在满载状态下,1阶垂向振动固有频率在0.92 Hz附近,与表6中同尺度船的波激共振频率比较接近。虽然并没有足够的研究证明和实际大型挖泥船发生波激振动的案例,但超大型化而引起船体梁1阶振动频率的降低,却足以引起设计人员在超大型挖泥船设计初期的高度重视。
4 结 论
由以上船体梁固有频率的估算与波激振动的论述可得到如下结论:
(1)挖泥船低阶垂向固有频率的估算可参考CCS关于散货船的直接简化计算公式;
(2)直接简化计算简单省力,而且在工程应用上比三维有限元方法具有更大的优势;
(3)随着挖泥船的大型化,大型船舶不可避免的波激振动问题在超大型挖泥船上同样不可避免;
(4)设计初期,对超大型挖泥船在总强度和节点设计方面均应考虑波激振动的影响成分,在总纵弯矩和节点设计上留出设计余量;
(5)波激振动对超大型耙吸挖泥船航行状态和正常作业状态的具体响应研究和影响尚待深入研究。
[1] 中国船级社.船上振动控制指南[S].2010.
[2] O.M.帕利,Г.В.巴依佐夫,著. 徐秉汉,徐绚,译.船舶结构力学手册[M].北京:国防工业出版社,2002.
[3] 金咸定,赵德友.船体振动学[M].上海:上海交通大学出版社,2000.
[4] 戚卫斌,倪海军. 双联挖泥船在宽水域施工中的共振分析[J].浙江水利水电专科学校学报, 2011,23(3):8-11.
[5] 汪雪良,胡嘉骏,顾学康,等. 超大型矿砂船波激振动及颤振研究[J].江苏科技大学学报(自然科学版),2010,24(2):120-124.
[6] 汪雪良,顾学康,胡嘉骏,等. 大型LNG船波激振动模型试验研究[J].中国造船, 2012,53(4):1-11.
[7] 汪雪良,顾学康,胡嘉骏. 基于模型试验与三维水弹性理论的船舶波激振动响应研究[J].船舶力学, 2012,16(8):915-925.
Study on free vibration of ultra large trailing suction hopper dredger
SUN Xue-rong QIAO Guo-rui
(Marine Design & Research Institute of China, Shanghai 200011, China)
The paper calculates the free vibration frequency of an ultra large trailing suction hopper dredger by the direct simpli fi ed calculation method and 3D fi nite element method. The direct simpli fi ed calculation method is based on the CCS calculation of the natural frequency of hull girders. The 3D fi nite element method builds the 3D fi nite element model of the hull by the commercial fi nite element software and directly carries out calculation combined with the elementary overall mass distribution. The aim of this paper is to seek appropriate estimation method about free vibration frequency of the girders of dredgers, and study the springing of ultra large dredgers due to the trend of macro-scale vessels and heavy usage of high strength steel.
free vibration; effective mass; effective stiffness; springing
U661.44
A
1001-9855(2014)03-0001-06

2014-01-03
孙雪荣(1980-),女,硕士,高级工程师,研究方向:船舶结构强度分析及振动噪声。
乔国瑞(1979-),男,高级工程师,研究方向:船舶结构设计。

