基于免疫与神经网络的RNA二级结构预测*

林 航,李金铭

(福建农林大学,福建 福州 350002)

脱氧核糖核酸具有重要的生物学功能，是DNA到蛋白质间遗传信息中间传递体[1]。RNA二级结构是特定平面图，配对的部分构成局部的双螺旋结构，这就是RNA的二级结构[2]，它是一种平面的结构。目前，使用实验方法在RNA信息数据的惊人的增长下，实现生物分子的具体的二级结构有着其自身的局限性，而且对所有分子并不是都有效的[3]。

研究表明，对RNA二级结构预测，通过计算机仿真与数学建模的方法具有较高的可信度和参考价值，主要的类型有：

(1)动态规划的方法

动态规划方法是基于热力学原理。Zuker动态规划算法为代表的[4]的动态规划算法，是自由能计算模型。该算法实现简单，但它不能预测带假结的RNA分子，由于其真实结构可能不是最低自由能，所以用这种方法来预测准确率低。

(2)比较序列法

比较序列的方法通常采用的是共变模型[5]和随机上下文无关语法模型[6]。通过比较序列的方法可以预测RNA二级结构更好，更准确，但他们需要更多的同源序列，并且对同源序列还有一定的限制要求，花的时间也较多。

由于上述方法的局限性，组合优化算法被提了出来。通过使用这种方法，模拟退火算法、遗传算法[7-9]、Hopfield神经网络[10-11]等启发式算法被用来解决该问题。本文采用混沌Hopfield神经网络算法预测RNA二级结构。

一、混沌理论

混沌是一种非线性现象，广泛存在于自然界中，它可能看起来有些混乱，但其精致的结构，使随机性、遍历性和规律性成为它的特点，某个范围内，其可以按自身的规律不重复遍历所有状态。

一般指的是通过随机确定性方程获得的随机性运动状态，混沌状态变量被称为混沌变量。logistic映射是是一个常用的混沌系统，方程如下：

Zn+1=μzn(1-zn) n=0,1,…n

(1)

式(1)是一个动力学系统，μ作为其控制参数。μ值确定后，从任意的初值 z0∈[0,1]，可以迭代得到一个确定的时间序列Z0,Z1，…Zn。 当μ=4 时，是一个完全处于混沌状态系统。混沌优化算法能够轻易的跳出局部最优解，归功于它的混沌性。它的搜索机制表现很好，常常被用于算法的混合中，并作了广泛研究。把混沌算子应用于遗传算法中，提出了混沌遗传算法，取得了较好的效果。把混沌搜索结合于微粒群算法，得到了混沌粒子群优化算法，都具有很好的搜索性能。

二、Hopfield神经网络

Hopfield神经网络是一个只有单一的神经元层次的结构，同时每个神经元与其他神经元的输出是相互连接的，称之单层反馈网络。0或者1两种值是Hopfield神经网络的取值集合。Yi(t+1)是神经元的输出，Xi(t+1)是网络的输出，如公式(1)：

Xi(t+1)=sgn(yi(t+1),i∈[1,n]

(2)

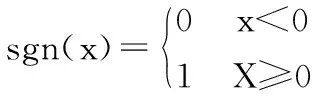
Hopfield神经网络在优化计算的应用中，目标函数有相应的能量函数，从而网络权值也被确定，当神经网络的能量达到最小时的解，就是问题的最优解。

三、混沌Hopfield神经网络优化算法求解

1.应用于RNA二级结构预测的Hopfield神经网络Hopfield神经网络用于RNA二级结构预测问题时，用基于最小自由能思想的茎区自由组合算法时，由于Vi=0表示该神经元被选中，能量函数可以写成[12]：

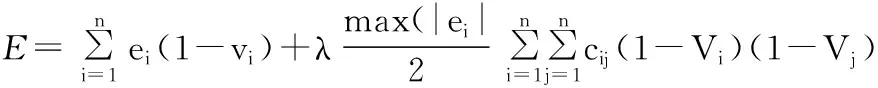
(3)

其中， cij即为节点i 和j 间的权值，茎是否被选中决定了Vi取0或1， ei表示茎i的能量；茎i 与j 是否相容来决定取值为0或1；非稳定茎和稳定茎间的相对率通过λ调整。

2.混沌Hofield神经网络算法描述

对于Hopfield神经网络来说，其对初始值的依赖性很强，因此本文使用距离函数产生初始解，对神经网络的初始解进行优化。对Hopfield初步产生的最优解，通过使用混沌函数对其值进行混沌化，使其跳出局部最优解，搜索全局最优解，其具体步骤如下：

(1) 定义问题，能量函数对应目标函数和约束条件，神经元的输出 Vi对应问题的解，初始化神经网络参数，令 T=max,t=0 ；

(2) 使用距离函数计算初始解，初始化神经网络；

(3) 初始化神经网络，选取一个还未被访问的聚类中心，为该神经网络神经元的初始输出；

(4) 当Ui>0 时，Vi=1 ，否则 Vi=0。而 Vi=0说明该碱基配对；

(5) 使用公式(4)中的定义的更新Ui，Vi；

(6) 当满足终止条件，即满足Ui(t+1)=Ui(t)+△Ui(t)△t或者△ Ui(t)或者t=max ，继续下一步, 否则转4)；

(7) 计算当前解的目标函数值；

(8) 使用混沌函数对初步初始解进行混沌化，产生新的初始值初始化神经网络;

(9) 达到最大迭代次数，优化终止，从中选取使目标函数值最小的解。

四、实验结果

1. 评价标准

敏感性(X)，特异性(Y)和马休兹相互作用系数 (MMC)是目前评价RNA二级结构准确率主要的3个度量参数。X是所有碱基对在真实结构中被正确预测到的比率。Y是正确预测所有预测到的碱基对的比率。一般折中衡量上述两个参数的是MCC。

2. 参数设置和仿真结果比较

仿真中，A=0.1,B=0.2 为神经挽留过的常量参数。最后得到实验结果见下表1。我们可以看出本文的算法优于其他算法。

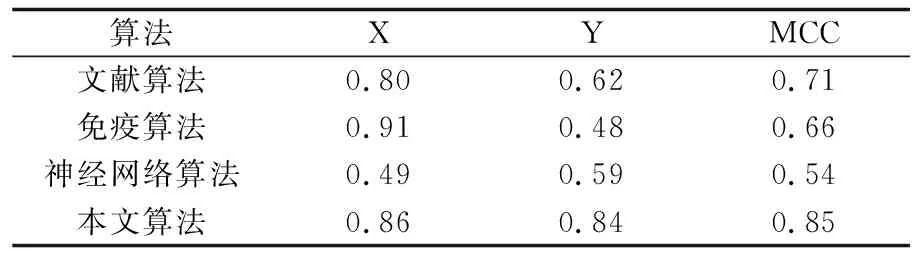
表1 4种算法平均预测准确率的比较

五、 结语

本文根据混沌算法的遍历性和随机性，和神经网络对初值的依赖性，结合RNA结构的保守性的特点，对神经网络的初值进行优化，将Hofield神经网络通过混沌函数进行优化，首次运用于RNA二级结构预测，提高了全局，搜索能力，使其不易陷入局部最优解，并获得一定的效果。

参考文献：

[1] 林娟,钟一文,张骏. 离散蛙跳算法预测RNA二级结构[J].南京师范大学学报(工程技术版), 2011，(4).

[2] 邢翀. RNA二级结构预测算法的研究[D].长春：吉林大学,2012.

[3] 林娟,钟一文. 改进的免疫粒子群优化算法预测RNA二级结构[J].计算机工程与应用, 2012，(1).

[4] ZUKER M. On finding all suboptimal foldings of an RNA molecular[J]. Science, 1989, 244(4900):48～52.

[5] Ennysr. Durbar RNA Sequence Analysis using covariance models[J].Nucleic Acids Res.1994,(22):2079～2088.

[6] Sakakbara Y,Browm M,Hugheryr.Recent methods for RNA modeling using stochastic context-free grammars[C]. Grochemorem.Gusfield D.Proceedings of the sikomar conference on combinatorial pattem matching Berlin:Springer-Verlag.1994:289～306.

[7] Cai L, Malmberg R. L, Wu Y. Stochastic modeling of RNA pseudoknotted structures: a grammatical approach [J]. Bioinformatics.2003:166～173.

[8] HU Yuh-Jyh. Prediction of consensus structural motifs in a family of coregulated RNA sequences [J]. Nucleic Acids Research , 2002 ,30(7) : 3886～3893.

[9] SHAPIRO B A , WU Jin-chu , BENGALI D , et al. The massively parallel genetic algorithm for RNA folding: MIMD implementation and population variation[J]. Bioinformatics , 2001 ,17 (2) : 137～148.

[10] WIESE K C , DESCHENES A A , HENDRIKS A G. Rna Predict-an evolutionary algorithm for RNA secondary structure prediction[J]. IEEE/ ACM Transactions on Computational Biology and Bioinformatics , 2008 ,(50) : 25～41.

[11] T AKEFUJI Y ,CHEN Li-lin , LEE K c, et al. Parallel algorithms for finding a near-maximum independent set of a circle graph[J]. IEEE Transaction on Neural Networks , 1990,1(3): 263～267.

[12]刘琦，张引，叶修梓. 基于离散Hopfield网络求解极大独立集的茎区选择算法以及在RNA二级结构预测中的应用[J]. 计算机学报，2008, 31(1): 51～58.