对2012年高考上海物理卷第12题答案设置科学性的质疑
谢 佳 刘洪庆
(仁怀市酒都高级中学 贵州 仁怀 564500)
笔者在教学中就2012年高考上海物理卷第12题进行实例分析时发现,该题的答案设置与实际解答分析得到的结果不相符,而该题的原解也显得比较牵强,缺乏必要的证据来佐证所选答案的合理性.现就该问题展开分析,以供同仁探讨.
1 原题和原解
1.1 原题
如图1所示,斜面上a,b,c三点等距,小球从a点正上方O点抛出,做初速为v0的平抛运动,恰落在b点.若小球初速变为v,其落点位于c,则
A.v0<v<2v0
B.v=2v0
C.2v0<v<3v0
D.v>3v0

图1
1.2 原解
如图2所示,M点和b点在同一水平线上,M点在c点的正上方.根据平抛运动的规律,若v=2v0,则小球落到M点.可见以初速2v0平抛的小球不能落在c点,只能落在c点右边的斜面上,故只有选项A正确.
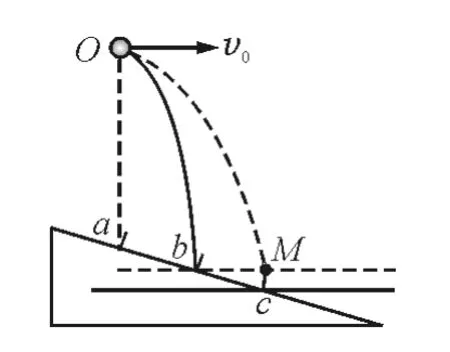
图2
2 对质疑之处的佐证分析
从该题的原解看,得出v<2v0确实没有问题,但仅凭上面的分析却不能佐证v>v0具有必然的合理性.故笔者认为选项A(v0<v<2v0)的正确性有待考证,现就该问题展开深度分析.
设Oa间距离为H,a到b和b到c的竖直距离为h,a到b和b到c间的水平距离为x.令小球从O点以初速度v0水平抛出落在b点历时t1,由平抛运动规律有
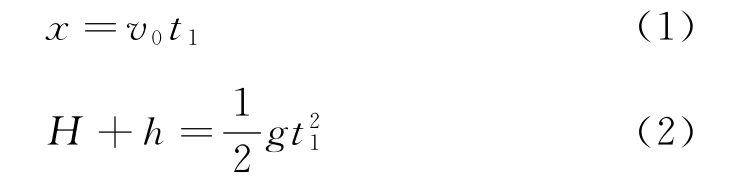
由式(1)、(2)可得
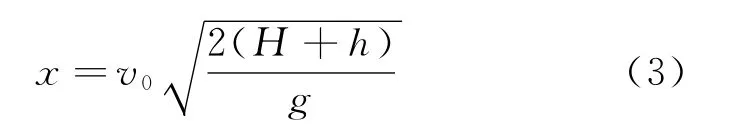
令小球从O点以速度v水平抛出落在c点历时t2,由平抛运动规律有

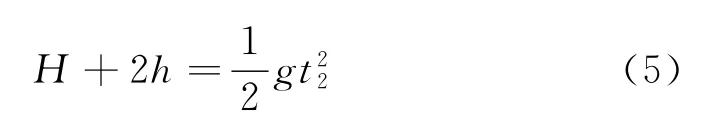
由式(4)、(5)可得
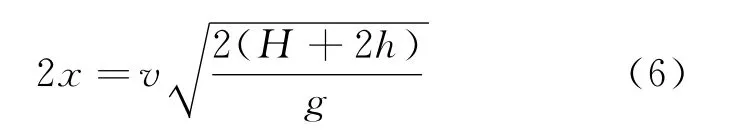
结合式(3)、(6)可得
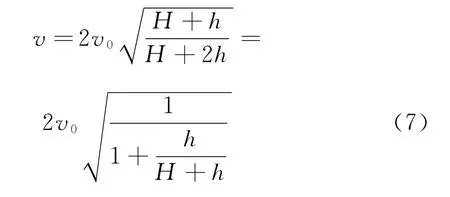
现对式(7)展开讨论:
当H→ ∞ 时,v→2v0,即可得v<2v0
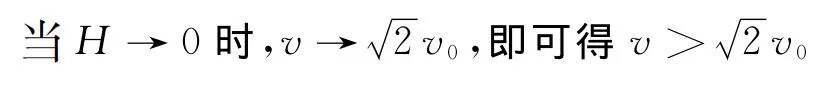
综上分析,小球落在c点时速度v满足的条件是.因此,选项A(v0<v<2v0)设置的科学性值得商榷.另说明,分别就h→0和h→!展开讨论,也可以得到相同的结果,这里不再赘述.
3 小结
就该高考题而言,A,B,C,D这4个选项其实都不满足题设要求,但也许是命题者的一小点疏忽导致了美中不足.文中观点是笔者在教学中的一些看法,希望各位同仁能再次求证.

