矩形激光脉冲辐照下半导体温度场理论研究

左惟涵，陈赵江，方健文，刘世清

(浙江师范大学数理与信息工程学院，金华321004)

引 言

随着微电子产业的高速发展，半导体材料作为电子产业重要的材料之一，其光热效应研究越来越受到重视，这需要发展高灵敏、高空间分辨率和快速简单的测量技术来检测半导体材料的特性。光声光热技术是一种基于光声光热效应建立起来的灵敏度高和有较高空间分辨率的非接触无损检测技术，目前已广泛应用于物理、化学、生物、医学和材料等领域［1-4］，特别是半导体材料和器件一直是光声光热检测技术的重要应用对象［5-7］。近些年来，ZHAO等人［8］提出了一种新的激光光热技术——阶跃光激励的光热技术。相比传统技术，该技术实验装置简单、测量快捷，因而越来越得到人们的关注。目前，阶跃光激励光热技术大多局限于普通固体材料的热学参量测量和表征，在半导体材料中的应用尚在起步阶段。ZHANG等人［9］基于本征函数法给出了阶跃光激励下材料温度分布的3维理论，但仅局限于一般固体材料;YE等人［10］求解分析了半导体材料中的1维温度分布，但是模型中没有考虑载流子表面复合速率的影响，且1维模型不能很好地和实验条件相符合。此外，以往关于阶跃光激励光热技术的理论研究均局限于温度瞬态分布的上升沿部分，对下降沿的情况没有进行讨论。

本文中根据半导体的光电效应和热传导规律建立了矩形激光脉冲辐照下半导体材料的3维理论模型，明确地给出了等离子体波和温度分布随时间变化的具体解析形式。通过数值模拟研究了矩形激光脉冲辐照下半导体内光生载流子浓度和温度的变化规律，对不同半导体参量如光生载流子复合速度、光生载流子寿命以及扩散速率等对变化规律的影响进行了分析。其次，讨论了矩形激光脉冲激励下半导体材料温度沿径向的扩散规律。此外，利用多参量拟合灵敏度以及相关性分析对利用阶跃响应脉冲信号表征半导体参量的可行性进行了阐述。

1 理论模型

当一束矩形激光脉冲垂直入射半导体样品表面时，如果入射光子的能量(E=hν，其中h为普朗克常数，ν为辐射电磁波频率)大于半导体的禁带宽度(即能隙Eg)，则在半导体体内将激发电子-空穴对，即光生载流子。然后在大约10-12s的弛豫时间内，载流子的过剩能量(hν-Eg)通过与晶格的碰撞将传递给晶格而转化为热能，使晶格温度上升。由于浓度梯度的存在，光生载流子将产生扩散，形成等离子体波。与此同时，伴随着电子-空穴的复合过程，其复合时间(即光声载流子的寿命τ)约为10-3s～10-9s。随着激发态的光生电子与空穴复合，其能量将传递给晶格，相当于对晶格形成又一次加热过程，使半导体温度场发生变化，形成热波。本文中采用的理论模型如图1所示，在模型中忽略空气介质的影响。

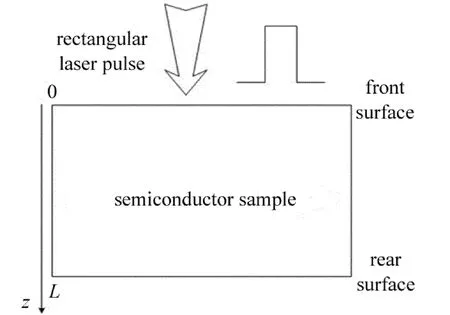
Fig.1 Theoreticalmodel of semiconductormaterials irradiated with rectangular laser pulse

在激光脉冲辐照下半导体内的瞬态光生载流子浓度分布 n(r，z，t)和样品中温度分布 Ts(r，z，t)满足如下扩散方程［11］:

式中，De是光生载流子的扩散率，τ是光生载流子的寿命，Dt，s为样品的热扩散率，r是样品表面径向距离，z是样品的纵向深度，光生载流子的产生速率Qe(r，z，t)和热源项 Qt( r，z，t)分别表示为:

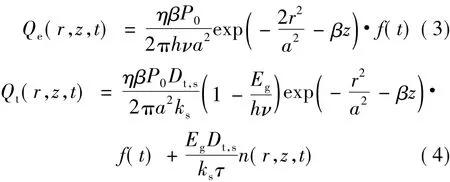
式中，η是量子效率系数，β是光吸收系数，P0是入射光功率，a是样品表面入射光斑半径，r是柱坐标径向分量，ks为样品的热导率，f(t)为矩形脉冲函数，可表示为:

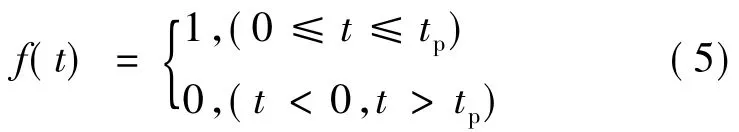
式中，tp是矩形激光脉冲宽度。(1)式满足如下边界条件:

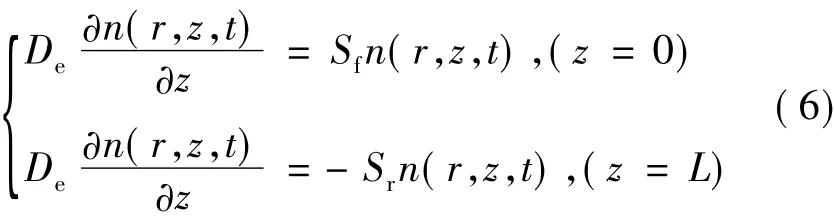
和

式中，Sf和Sr分别为样品前表面和后表面的光生载流子复合速率，L为样品厚度。

对(1)式分别作Hankel变换，并用z方向的本征函数法［12］展开:

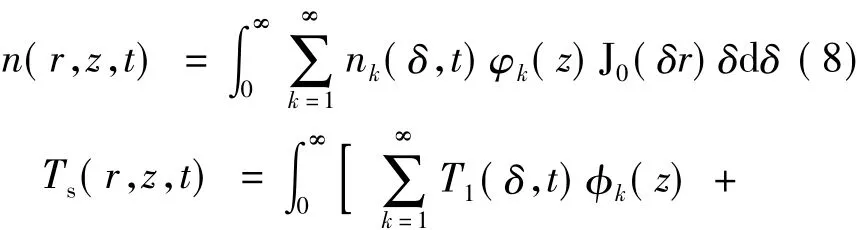
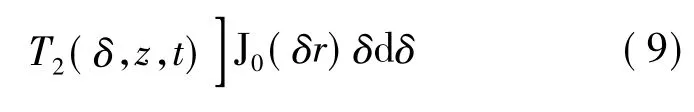
式中，本征函数φk(z)和φk(z)的具体推导过程和表达式可见参考文献［12］，δ是r经汉克尔变换后的对应的新变量，J0(δr)为汉克尔变换对应的零阶贝塞尔函数，T1(δ，t)φk(z)为对边界条件(7)式齐次化后求得的温度场，T2(δ，z，t)为对边界条件(5)式进行齐次化处理所得的附加项:

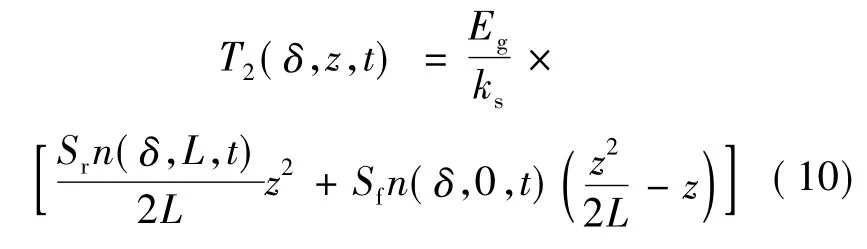
将(8)式代入(1)式进行Laplace变换，并应用卷积定理，然后将f(t)的表达式代入，整理可得:

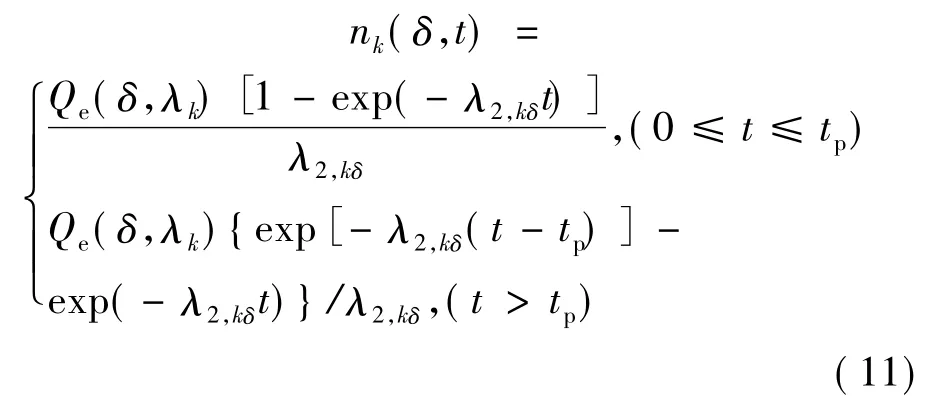
式中，tp表示阶跃时间λk是对应 φk(z)的本征值。将(11)式代入(8)式即可得瞬态光生载流子浓度分布n(r，z，t)。

同理，经整理后T1(δ，t)φk(z)可以写成如下形式:

式中，将nk(δ，t)中的时间t和求和项k分别用积分变换和 j表示，得到 nj(δ，ξ)，nj'(δ，ξ)表示的是nj(δ，ξ)对时间 t的1 阶偏导数。Qt(δ，λk)=G(δ) ×将(12)式和(10)式代入(9)式，即可得半导体中温度场的瞬态分布。

2 结果与讨论

根据理论模型对其进行数值计算，所使用的参量如下:半导体材料厚度L=0.5mm，热导率ks=142W·m-1·K-1，热扩散率 Dt，s=8.42 ×10-5m2/s，光吸收系数β=2.4×106m-1，禁带宽度Eg=1.79×10-19J，激光功率P0=1W，光斑半径a=1mm，入射光子能量 hν=3.97×10-19J。

图2为不同载流子参量情况下根据上述理论模型计算得到的矩形激光脉冲辐照下光生载流子浓度n(r，z，t)随时间t的变化规律。从图2a中可以看出，随着载流子上表面复合速率Sf的增加，曲线上升越快，光生载流子浓度达到平衡时所用的时间越短，但其幅值却越小;其下降速率也越来越快。从图2b中可看出，随着载流子寿命τ的增加，曲线上升得越慢，光生载流子浓度达到平衡时所用时间越长，其幅值也随之变大;其下降的速率也越慢。从图2c中可以看出，随着载流子扩散速率De的增大，其下降速率也越快。光生载流子浓度达到平衡时所用的时间越短，但是幅值却越小，从(11)式可以看到时间项只和指数项有关，此项中的衰减系数λ2，kδ决定了曲线变化的快慢。而衰减系数的大小是由载流子上(下)表面复合速率Sf(Sr)、载流子寿命τ以及载流子扩散速率De共同决定的，这些参量是造成了载流子浓度上升和下降快慢的主要因素。

图3是根据模型计算得到的不同载流子参量情况下，样品表面中心温度随时间变化的规律，从图3a中可以看出，随着载流子上表面复合速率Sf的增加，温度幅值越大;从图3b中可以看出，随着载流子寿命τ的增加，温度幅值随之变小;从图3c中可以看出，随着载流子扩散速率De的增大，温度的幅值也随之变大;从图3d中可以看出，随着热扩散速率Dt，s的增大，幅值虽无变化，但达到平衡时所用的时间缩短。这是因为材料的热扩散率越大，热量在材料中的传递速度也就越快，那么样品达到稳态所需要的时间就越短。从(12)式中的指数项可以看出，热扩散系数的大小对温度曲线变化快慢有非常重要的影响。对比图2和图3，由于半导体样品的热扩散系数Dt，s=8.42×10-5m2/s比载流子扩散速率De=1.5×10-3m2/s小很多，因此图3中的曲线达到稳定的时间与图2相比更长。此外，从图3可知，不同参量条件下温度上升曲线比温度下降曲线的差异更为明显，其原因可能与热波的扩散过程有关。

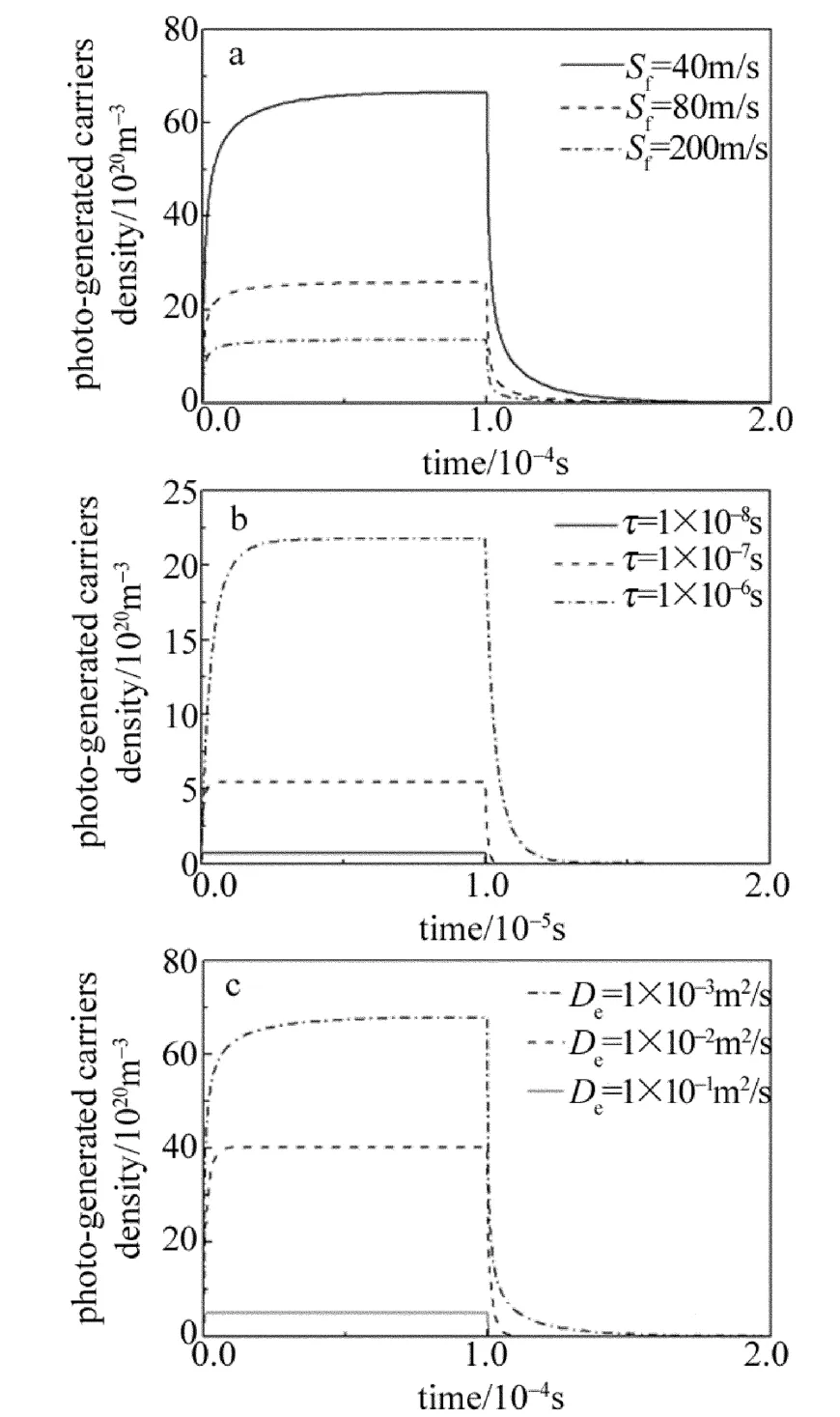
Fig.2 Time evolutions of photo-generated carriers density at the surface center for differentmaterial parameters a—different surface recombination rates Sf b—different photogenerated carriers lifetimesτ c—different photo-generated carriers diffusivity De

此外，作者对样品表面温度随径向距离的分布情况也进行了计算。从图4a可知，随着激励光光斑半径的增大，靠近加热光束中心位置的温度快速衰减而温升在径向的分布范围增大。这是因为激励光功率不变而光斑变大，光能量密度减少的缘故。因此，在光热检测时需激光光斑半径较小以在加热光束中心位置得到较为明显的温升。此时，为了能够准确地表征光斑中心及其周围温度场必须要使用3维模型。从图4b可以看出，随着光照时间的增加样品温度快速上升，与此同时样品表面的温度随径向距离快速扩散。根据这个特性，可以用矩形激光脉冲辐照的光热技术获得样品表面的光学和热学信息。

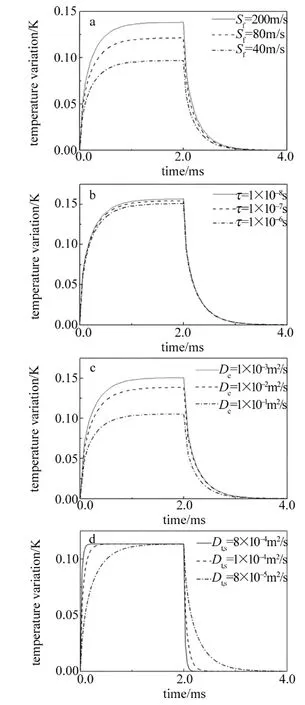
Fig.3 Time evolutions of temperature variation at the surface center a—different surface recombination rates Sf b—different photo-generated carriers lifetimesτ c—different photo-generated carriers diffusivity De d—different thermal diffusivity Dt，s

在利用阶跃光激励光热技术表征半导体材料参量时主要是采用基于最小二乘法原理的多参量拟合方法，即利用光热信号模型对阶跃响应实验信号进行拟合使其误差平方和函数最小，从而来确定待测的半导体材料参量［13］。在多参量拟合时，需考虑所用数学模型中待求参量对信号的灵敏度以及各参量间的相关程度。当待求参量灵敏度很小或待求参量之间存在线性依赖时，拟合时很难得到收敛和稳定的解。从图2和图3可知，表面复合速率Sf、载流子寿命τ和载流子扩散率De参量变化时，其等离子体波和热波阶跃响应曲线具有类似的特征。因此，能否利用阶跃响应曲线同时确定上述3个未知半导体参量需进一步研究。利用参考文献［14］中给出的方法对此问题进行了分析，并在图5中给出了一个典型的数值模拟结果。图5中3条曲线分别代表上述3个参量对等离子体波阶跃响应信号的灵敏度。从图可知，不同参量对阶跃响应信号的灵敏度存在差异，灵敏度系数越高，对应参量的拟合精度越好。对于图5中设定的参量值，表面复合速率Sf容易精确拟合得到。此外，从图中也可发现不同参量灵敏度系数的相关性不同，相关性系数越大，则同时拟合得到这两个参量越困难。在图5中Sf和τ的参量灵敏度相关性高达0.89，因此这两个参量组合［Sf，τ］难以同时拟合得到。而其它两种未知参量组合［Sf，De］和［τ，De］的灵敏度相关性分别为 0.68 和0.51，因此是可以通过参量拟合的方法同时确定的。

Fig.4 Temperature distribution at the sample surface along radial distance a—different spot radius a b—different time t

3 结论

建立了矩形激光脉冲激励下半导体材料温度分布的3维理论模型，采用本征函数展开法求得了半导体中光生载流子浓度和温度分布解析表达式。通过数值模拟分析了不同参量条件下半导体内光生载流子浓度和温度随时间的变化规律。结果表明，矩形脉冲激光激励下光生载流子表面复合速率、光生载流子寿命和载流子扩散系数对半导体材料的温升的阶跃响应曲线具有重要影响。同时，由于半导体的热扩散率与载流子扩散率相比较小，温度场达到稳定所需要的时间比光生载流子浓度达到稳定所需要的时间长，因此，通过测量温升曲线的变化更容易对半导体材料参量进行表征。此外，脉冲激光的光斑半径与辐照时间的不同对温度场时间与空间的分布也会产生不同的影响。上述结果表明，利用矩形激光脉冲辐照的光热技术可以对半导体材料特性进行表征。

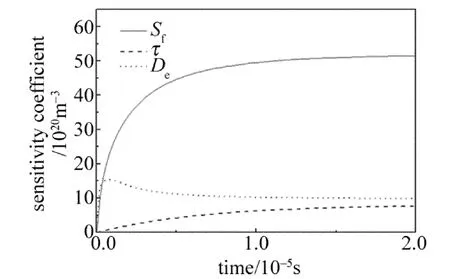
Fig.5 Sensitivity coefficients of step response signal of plasma wave for surface recombination rates Sf，photo-generated carriers lifetimes τand photo-generated carriers diffusivity De(among them Sf=40m/s，τ=10-5 s，De=1.5 ×10-3 m2/s，other parameters are the same as above)

［1］ZHOU J，MA Zh H，PANG X R，et al.Research on transient state temperature field of the surface ofmetalmaterial under pulsed laser radiation ［J］.Applied Laser，2010，30(1):1-5(in Chinese).

［2］LIQ Sh，LUOH，HU YM，etal.Analysisof characteristics ofacoustic waves induced by triangular laser pulses［J］.Laser Technology，2010，34(3):409-412(in Chinese).

［3］PEI X，WU JH.Numerical simulation of transient temperature field onmetalmaterial induced by pulse laser irradiation［J］.Laser Technology，2012，36(6):828-832(in Chinese).

［4］WANG H E，SHEN R Q，YE Y H，et al.Effect of reagent ratio of graphite to potassium nitrate on reactive photoacoustic characteristics［J］.Laser Technology，2013，37(2):274-276(in Chinese).

［5］ZENG H L，ZHANG X R，GAPCh M，et al.Application on laser-induced photothermal technique to semiconductor property measurement［J］.Optoelectronic Technology，2009，29(3):211-215(in Chinese).

［6］IKARI T，SALNICK A，MANDELIS A.Theoretical and experi-mental aspects of three-dimensional infrared photothermal radiometry of semiconductors［J］.Journal of Applied Physics，1999，85(10):7392-7397.

［7］WARRIER A R，DEEPA K G，SEBASTIAN T，et al.Non-destructive evaluation of carrier transport properties in Cu InS2and CuInSe2thin films using photothermal deflection technique［J］.Thin Solid Films，2010，518(7):1767-1773.

［8］ZHAO JH，ZHOU JQ，SHEN J.Thermophysical propertymeasurements using time-resolved photothermal deflection spectrometry with step optical excitation［J］.Applied Physics Letters，2004，84(26):5332-5334.

［9］ZHANG X L，CHEN Zh J，SU X Q，et al.Three-dimensional theory of temperature distribution for solid materialswith step optical excitation［J］.Applied Laser，2011，30(5):433-438(in Chinese).

［10］YEM Q，CHEN Zh J，FANG JW，etal.Temperature variation of semiconductors with step optical excitation ［J］.Journal of Zhejiang Normal University(Natural Science Edition)，2011，34(3):286-291(in Chinese).

［11］BOCCARA A C，FOURNIER D，MANDELIS A.Photoacoustic and thermalwave phenomena in semiconductors［M］.New York，USA:Elsevier，1987:290-310.

［12］CHENG JCh，ZHANG Sh Y.Theoretical studies of pulsed photothermal phenomena in semiconductors［J］.Journal of Applied Physics，1993，74(9):5718.

［13］MANDELIS A.Laser infrared photothermal radiometry of semiconductors:principles and applications to solid state electronics［J］.Solid-State Electronics，1997，42(1):1-15.

［14］CHEN Zh J，FANG JW，WANG Zh H.Thermal characterization of film-on-substrate systems by laser photothermal reflectance technique［J］.Chinese Journal of Lasers，2006，33(3):385-390(in Chinese).