基于神经网络的精密磨床床身结构优化研究*

柯晓龙 林晓辉 王春锦

(①厦门理工学院机械与汽车工程学院，福建 厦门361024;②厦门大学物理与机电工程学院，福建 厦门361005)

目前，轴对称非球面、离轴非球面、楔形非球面等大尺寸光学非球面元件在航天、航空、国防等领域中得到了越来越广泛的应用。由于其应用领域的特殊性和精密性，对光学非球面元件的面形精度和表面粗糙度提出了极高的要求。而磨床的一些关键特征，如机床刚度、固有频率等，对其精密加工有着很大的影响。因此，如何有效地优化磨床的刚度和固有频率，是高精密磨床设计过程中的必须要解决的重要课题。

机床的结构与刚度优化的方法有很多种，有限元软件分析和灵敏度计算是当前较为主流的分析方法［1-4］。如清华大学的汪劲松教授等人［5］在UGNX 2.0和ANSYS 8.0环境下建立重型混联机床XNZH2430的三维模型和有限元模型，并采用有限元方法分析其静刚度，研究该机床在不同形位时承受一定载荷所引起的变形位移情况，从而优化机床承载力刚度。东南大学的伍建国教授等人［6］采用灵敏度分析的手段，找出对内圆磨床床身结构动态特性影响较大的设计参数，以保证床身设计具有较好的动态特性及刚性。

而本文则采用有限元分析和BP神经网络计算结合的办法，利用有限元的方法对自主开发的高精度磨床2MK1760的床身进行静力分析和模态分析，同时利用BP神经网络来优化磨床结构，以达到提高磨床刚度和固有频率的效果。

1 高精度磨床结构分析

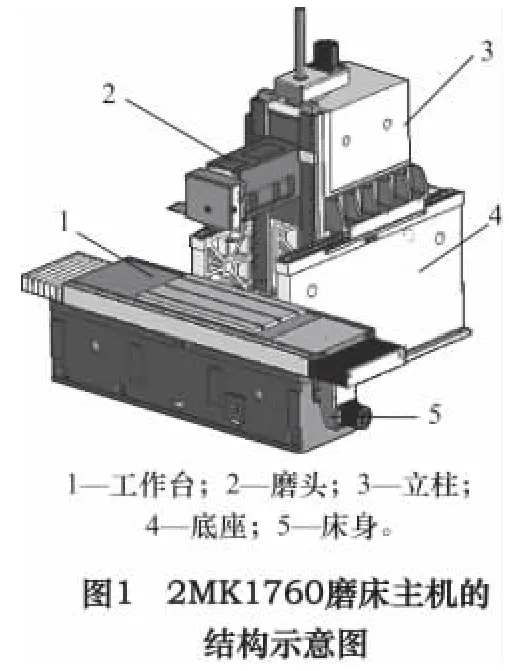
本文自主开发的高精度磨床2MK1760，采用立柱移动式卧轴矩台平面磨床结构，专门用于硬脆性材料，如熔石英、BK7玻璃等光学非球面元件的精密磨削加工。该磨床采用T字形布局，外围加钣金全防护罩防护，工作尺寸达到1 000 mm×600 mm×650 mm，机床设计加工精度为±2μm/430 mm×430 mm。磨床整机由床身、工作台、立柱、底座、磨头、电气及数控系统、光栅反馈系统、液压系统、油冷水冷系统、磨削液过滤系统、润滑系统、油雾净化装置、砂轮修整器、动平衡系统、外围防护罩、电磁吸盘等组成［7］。其中，磨床主机的三维结构图如图1所示。

为了保证良好的运动平稳性，床身与工作台的连接采用了精密液体静压导轨支撑。作为2MK1760磨床最为重要的部件之一，床身的变形及振动将影响磨床的运动定位精度，从而导致工件的精密磨削产生一定的加工误差，因此对磨床床身的分析就显得尤为重要。为了分析和优化磨床床身的结构，将采用如下4个步骤:(1)建立有限元模型;(2)获得静态和动态特征;(3)建立神经网络模型并分析;(4)利用上述结果，对磨床床身进行优化。

1.1 静态结构分析

为了完成磨床床身的静态特征分析，利用SolidWorks软件完成床身的三维实体建模，然后将其导入有限元分析软件ANSYS中形成有限元模型，并加以分析。床身材料选用HT300，材料及结构参数如表1所示。在本文中，工作台和工件的重量以及磨削法向力作为外部力施加在磨床的导轨上，整个床身被固定在底板和底座上。图2为工作台达到极限位置时，磨床床身的总变形位移。通过分析可知，床身最大变形位移为1.153μm。

1.2 模态分析

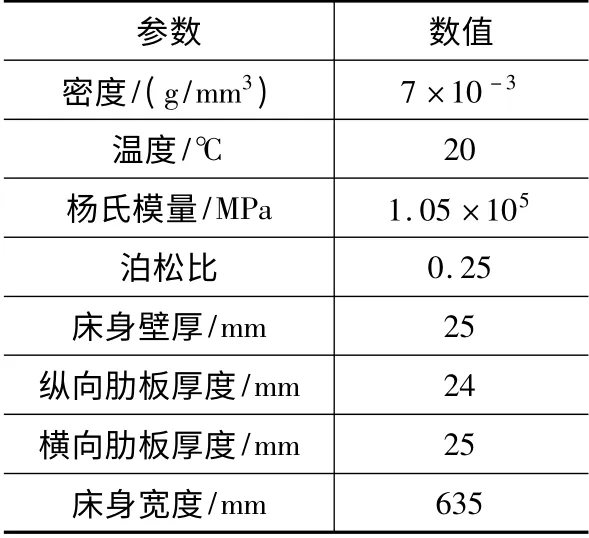
表1 床身的材料及结构参数

动态特征分析方法包括模态分析、频谱分析和瞬态静力分析。其中，频谱分析和瞬态静力分析一般适用于变化的外力。由于本文中床身的受力相对不变，因此只考虑模态分析。模态是固有的振动特征，每个模态都有自己的频率。为了便于分析对比，本文仅取一阶模态作为分析优化对象。经过分析计算，可以得到第一阶频率及振态如图3所示，其频率为464.8 Hz。

2 基于神经网络的结构分析

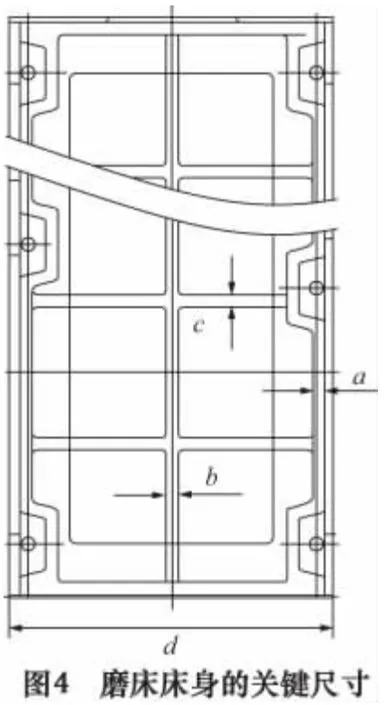
根据设计及实践经验，床身的壁厚a、纵向肋板厚度b、横向肋板厚度c和床身宽度d是关键的结构尺寸，因此将它们作为重要影响参数加以分析。图4是这些尺寸在磨床床身中的示意图。由于很难直接找出这些尺寸与变形量、频率之间的关系，因此本文利用神经网络来确定它们之间的关系。

BP神经网络包括3层:输入层、隐含层和输出层。对于本分析而言，结构变量Δa、Δb、Δc和Δd作为神经网络的输入参数，变形量dm和频率fz为输出参数。可以得到神经网络的结构图如图5所示。

输出的隐含节点yi为:

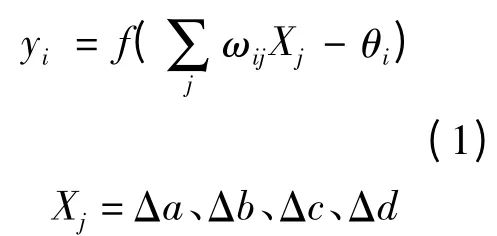
输出的节点为:

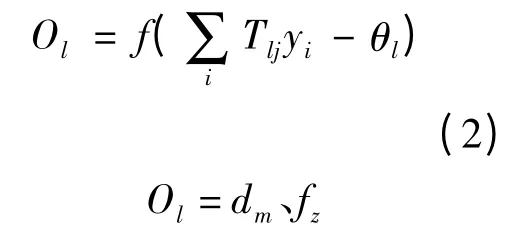
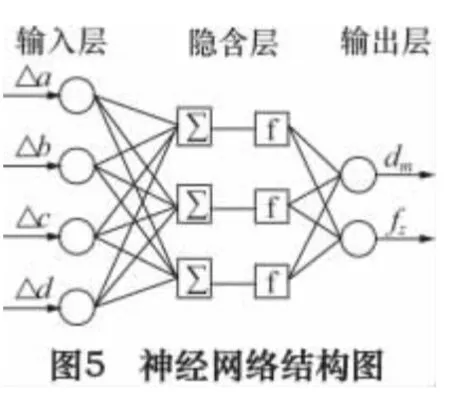
式中:ωij是输入节点与隐含节点的连接权重;Tlj为隐含节点与输出节点的连接权重;θi和θl是节点阈值。

而节点和隐含节点的误差E表示为

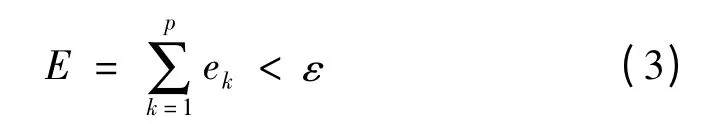
式中:ek是单项误差;ε为训练的目标误差。

根据以上的BP神经网络算法，结合大量的输入参数进行训练。测试的实际的变形值和频率是通过ANSYS计算完成的。经过神经网络训练后获得的结果如图6和图7所示。可以看出，预测值和实际值很相近。

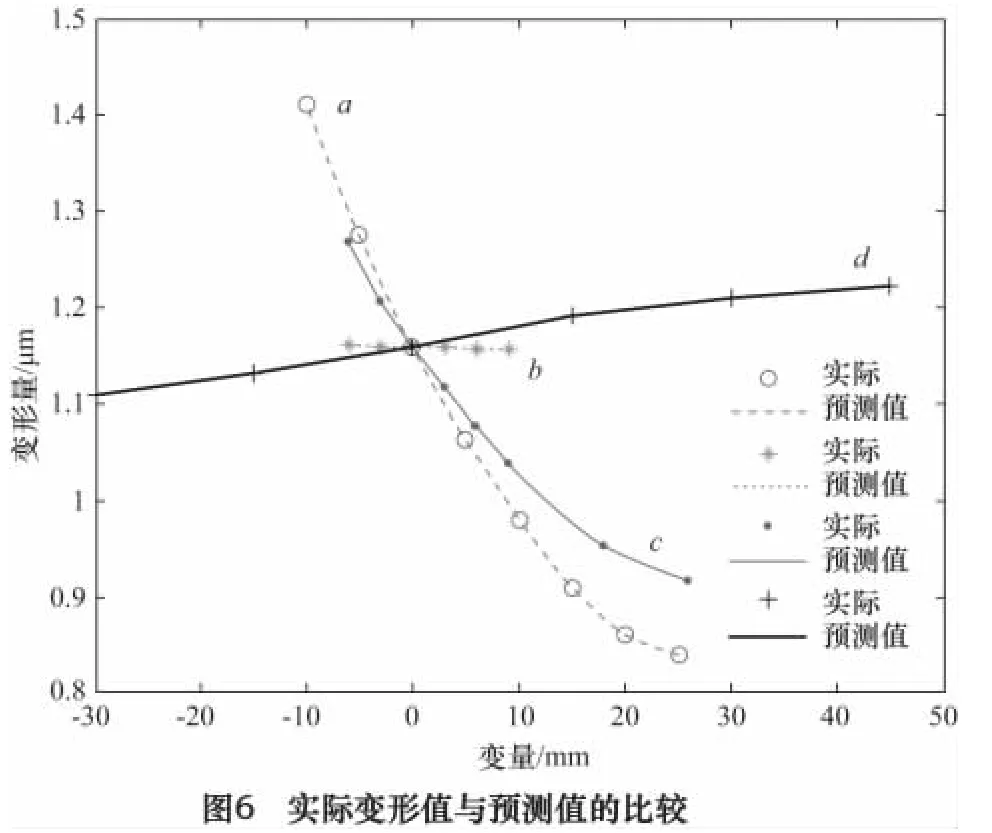
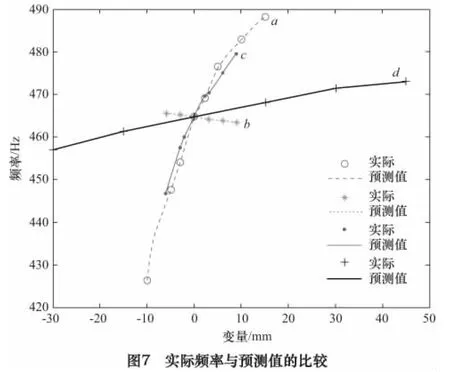
表2显示的是其他一些样本的预测值，同样可以看出预测值和实际值相近且误差小于1%。结果表明，BP神经网络可以较为准确地映射磨床的主要特征与结构参数之间的关系。

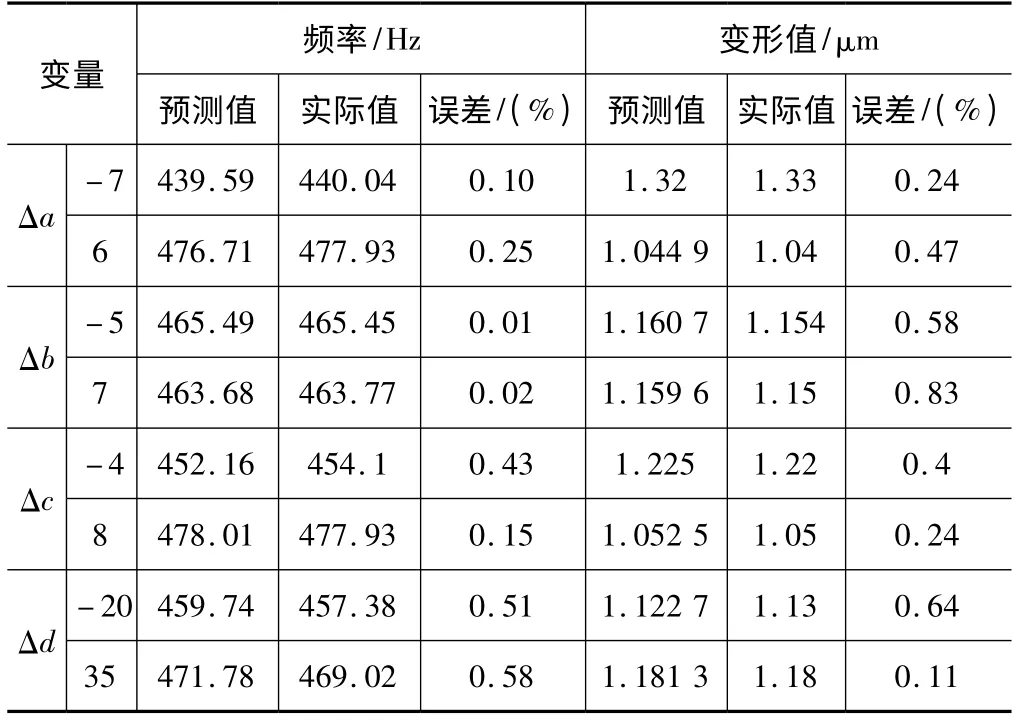
表2 测试结果(a、b、c、d)

由图6和图7可知，频率和变形值相对a和c较敏感，而相对b和d影响较小。基于此结果，我们建立另一个基于参数a和c的神经网络模型，将参数a和c作为输入参数，输出参数仍然是频率值dm和变形值fz。表3是该神经网络模型的测试结果。可以看出，其误差小于3%。

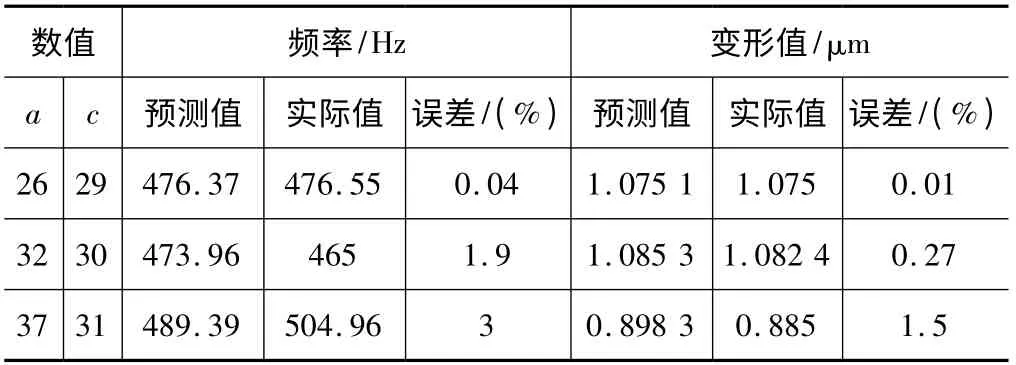
表3 测试结果(a、c)

3 磨床床身的优化

根据以上的分析结果可以看出，床身的宽度d和纵向肋板厚度b对床身变形和频率影响不大，而壁厚a和横向肋板厚度c的影响则很大。所以，床身宽度d和纵向肋板厚度b的尺寸可以相对小些，以减轻床身重量;同时，壁厚a和横向肋板厚度c则应作为变量进行优化。显然，对于高精度磨床而言，变形是影响精度最主要的因素，故将减小变形量作为优化目标。目标函数可以表述为:

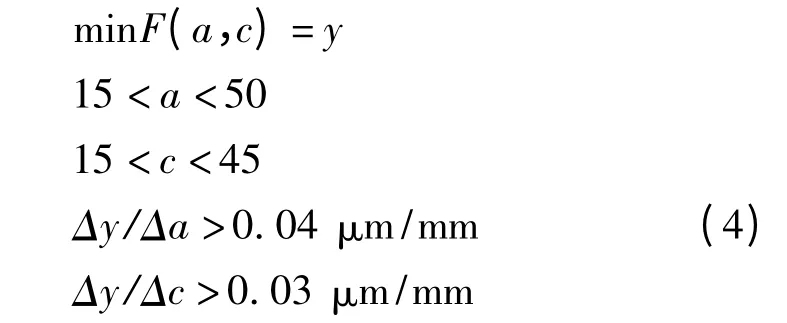
式中:Δy/Δa和Δy/Δc是敏感因子。

结合加工过程和实际的工况，约束条件也列在公式中。经过优化后，床身壁厚a和横向肋板厚度c都由之前的25 mm优化为41 mm，纵向肋板厚度b由之前的24 mm优化为20 mm，床身宽度d由之前的635 mm优化为605 mm。利用新的参数进行建模，得到新的总变形量和模态频率分别如图8、图9所示。

从表4可以看出，对比优化前的结构，优化后的床身结构的最大变形量从1.153μm下降到0.732μm，降幅达到36.51%。而一阶模态频率从464.8 Hz上升到520.4 Hz，涨幅达到11.96%。

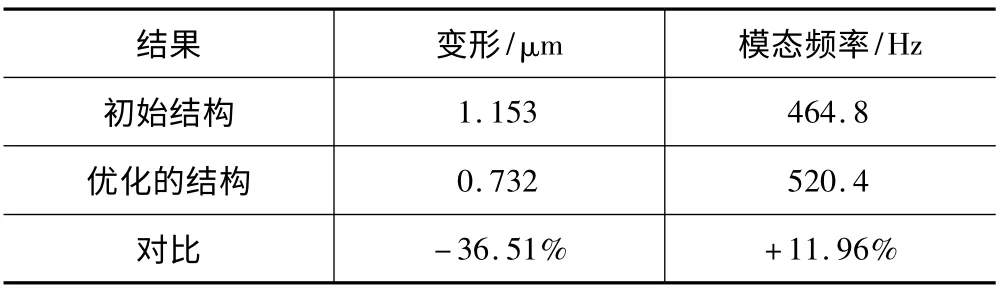
表4 优化结果对比

4 结语

本文使用两种BP神经网络模型来完成自主开发的2MK1760磨床的床身结构分析与优化。其中，利用第一种模型进行敏感度分析，进而确定敏感尺寸，然后代入第二种模型进行结构优化。

分析结果表明:(1)BP神经网络可以正确地反应磨床床身的关键尺寸与关键特征间的关系。(2)优化是可行的。通过确定敏感尺寸，并修正磨床床身的相关尺寸，可以较好地改善床身变形量和固有频率。(3)该优化方法同样可以应用于该磨床其他重要部件，如工作台、立柱、底座等部件的结构分析，以此提高机床的总体结构性能。

［1］Jiang Chen，Guo Yinbiao.Grinding precision forecasting in optical aspheric grinding using artificial neural network and genetic algorithm［C］.5th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Advanced Optical Manufacturing Technologies，April 26-29，2010，Dalian，China.

［2］满忠伟，汪世.基于神经网络的机床-工件系统热误差补偿技术研究［J］.制造技术与机床，2011(7):99-102.

［3］倪晓宇，易红，汤文成，等.机床床身结构的有限元分析与优化［J］.制造技术与机床，2005(2):47-50.

［4］Kang Yuan，Chang Chuan-Wei，Huang Yuanruey.Modification of a neural network utilizing hybrid filters for the compensation of thermal deformation in machine tools［J］.International Journal of Machine Tools＆Manufacture，2007，47:376-387.

［5］刘悦，汪劲松，王立平.重型混联机床XNZH2430的静刚度优化［J］.清华大学学报:自然科学版，2006，46(8):1418-1421.

［6］伍建国，陈新，毛海军，等.内圆磨床床身设计参数的灵敏度分析及动态设计［J］.南京航空航天大学学报，2002，34(6):544-547.

［7］柯晓龙，郭隐彪，张世汉，等.高精度光学元件磨床的加工与检测系统的开发［J］.厦门大学学报:自然科学版，2011，50(3):559-562.