一种利用范数性质的无约束盲均衡准则
王大磊, 杨 宾, 吴 瑛, 王秀秀
(1. 信息工程大学 信息系统工程学院,河南 郑州 450002;2. 西安电子科技大学 综合业务网理论及关键技术国家重点实验室,陕西 西安 710071)
在数字通信中,作为克服码间干扰(Inter-Symbol Interference,ISI)的重要手段,均衡技术受到广泛研究[1].由于盲均衡方法无需训练序列,可以节省带宽资源,且适合多点通信和非协作接收等场合,因此,涌现出了大量的盲均衡方法.典型的有Bussgang类型,如恒模(CMA)算法[2]、多模算法[3-4]和混合算法[5]等.此类算法基于某种非最小均方误差(MSE)的代价函数,采用随机梯度法求极值,计算量小,实现简单.然而,由于这类代价函数大都为非凸的,往往会局部收敛,导致不能充分消除ISI.
Shtrom和Fan依据向量范数的性质,提出了一类迫零盲均衡算法Shtrom-Fan算法(SFA)[6],此类代价函数在信道与均衡器联合响应域不存在假峰,能够保证全局收敛.然而,SFA算法需要固定均衡器的某一个系数或对其归一化约束,致使均衡器输出与发送信号的增益比不为1,需要自动增益控制,且这种约束方法对均衡器收敛性能的影响并没有严格的数学证明.之后,Abrar等[7]同样利用向量范数性质,结合星座图特点,提出了一种自适应的盲均衡算法βCMA.然而,该算法的参数是依据Bussgang的特性得到的,只反映了信号的部分统计特征,致使算法收敛后的稳态误差较大.基于以上考虑,笔者依据向量范数性质,结合文献[8]中将约束方程转换为无约束方程的方法,给出了一种新的无约束盲均衡准则,证明了在无噪声情况下,在代价函数的局部最优解处可实现理想均衡,且能够实现发送信号幅值的恢复.可采用批数据处理和在线自适应迭代两种方法更新均衡器系数,无需自动增益控制,实现简单,同时稳态误差更小.
1 系统模型
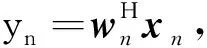
2 新的无约束盲均衡准则
2.1 SFA算法及βCMA算法

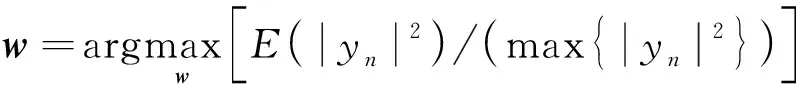
其中,γ为发送符号的最大幅值.然后,通过拉格朗日乘子法将约束条件引入到目标函数,得出一种自适应的迭代算法βCMA,即
wn+1=wn+μφ(yn)*xn,
(1)
其中,φ(yn)为误差函数,可依据Bussgang特性求得.当|yn|<γ时,φ(yn)=yn;当 |yn|=γ时,φ(yn)=0;当 |yn|>γ时,φ(yn)=-βyn,β由发送信号的平均能量以及星座图决定.尽管该算法能够恢复发送信号的幅值,但由于其参数是依据Bussgang特性得到的,只反映了信号的部分统计特征,致使算法收敛后的稳态误差较大.
2.2 新的无约束盲均衡准则

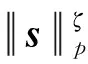
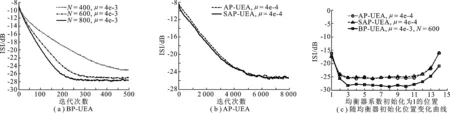
其中,p,q和ζ为实数,且0 (2) 其中,f: [0,∞]→R1,为一个分段连续实函数;g(x)=x2+f(x),是在0≤x<1区间内单调递增,在x>1 区间单调递减的函数,并在x=1 处取得最大值.代价函数建立后,需要考察它的收敛性和极值点的分布问题.下面给出关于该代价函数收敛性的两个定理. 定理1 当且仅当{si}序列中只有1个非零元素,且幅度为1,即s=δ(i-k) exp(jθ)时,J(s)取得最大值. 证明 由向量范数性质可得 定理2J(s)不存在假峰,即任何局部极大值解均对应理想均衡条件. 证明J(s)的平稳点满足 (3) 式(3)的解为具有M个相同幅度元素的向量,且幅度aM满足 2aM+f′(MaM)=0 . (4) 式(5)中,当α≠0时,不等式严格成立.因此,sM在M≥2时,不是局部极大值点. 因此,sM在M≥2时,也不是局部极小值点.从而这些点都是鞍点.综上,J(s)平稳点中只有解向量集s1是局部极值点,同时也是全局最优解.证毕. 定理1保证了代价函数能够取得最大值,定理2保证了代价函数的收敛性,采用随机梯度法时能够寻找到最大值. 为得到算法的具体形式,考虑一个二次函数,g(x)=-a(x-1)2+a,a>0,该函数满足 0≤x<1 区间内单调递增,x>1 区间单调递减的性质.此时,代价函数为 (7) 由于该代价函数是定义在s域的,而s不能直接得到,要想将代价函数应用于盲均衡,必须将代价函数转换为均衡器输出{yn}的函数.在无噪声情况下,有 (8) (9) 其中,γ=max{|an|}.将式(8)和式(9)代入式(7)中,得到 (10) 该代价函数同大多数盲均衡算法[6,8,10]一样,是在理想的无噪声情况下得到的.然而实际中信道噪声是存在的,对该代价函数的优化不能保证实现完全均衡.下面对有噪声情况下算法的性能进行讨论.由于s=wHH,则wH=sH-1,此时,式(8)修正为 (11) (12) 算法的两种具体实现方式: 基于一段数据的批处理方法和在线自适应迭代方法. 采用随机梯度下降法更新均衡器权值: (14) (15) 将式(16)和式(17)代入方程式(15),得到 (18) 归结起来,批数据处理算法步骤如下: 步骤1 收集一段长度为N的信道输出数据,计算均衡器输入向量的协方差矩阵的期望E[Xn],并初始化均衡器. 步骤2 计算均衡器输出序列{yn}. 步骤3 根据式(14)和式(18)计算新的均衡器权值,重复迭代直至收敛. 将式(14)和式(18)组成的批数据处理方法命名为批数据处理的无约束盲均衡算法(Batch Processing Unconstrained Equalization Algorithm,BP-UEA). (19) (20) 其中,误差函数Φ(yn)为 (21) (22) (23) 将式(14)、式(20)和式(23)组成的自适应迭代方法称为简化的自适应无约束盲均衡算法(Simplified Adaptive Processing Unconstrained Equalization Algorithm,SAP-UEA). 为了验证文中算法的性能,可选取同样基于向量范数性质的βCMA和SFA算法进行性能对比.在仿真中,如未特殊说明,条件统一设置如下: 均衡器输入信号的叠加噪声为高斯白噪声,信噪比为 30 dB;均衡器阶数为15阶,初始化时中心抽头为1,其他系数为0;AP-UEA和SAP-UEA算法中的参数p和a分别设为10和1,实验次数为100次. 对文中算法的3种实现方法BP-UEA、AP-UEA和SAP-UEA的有效性进行了仿真验证.信道采用文献[12]中图2所示的语音通信信道,信号采用16QAM调制的独立同分布信号源.图1(a)为BP-UEA算法的剩余ISI随迭代次数的变化曲线,在步长相同时,N越大,收敛速度越快,稳态误差越小.图1(b)为AP-UEA算法和SAP-UEA算法剩余ISI随迭代次数的变化曲线.可以看出,两种自适应算法的性能几乎无差别.相比自适应方法,批数据处理算法BP-UEA需要的样点个数少,适合短时、数据量少的场合. 图1 BP-UEA,AP-UEA和SAP-UEA算法的剩余ISI曲线 为验证不同的初始化条件对均衡器性能的影响,对3种处理算法BP-UEA、AP-UEA及SAP-UEA进行如下仿真: 仿真条件同上,均衡器系数初始化为1的位置依次改变,得到剩余ISI随不同初始化位置改变的曲线如图1(c)所示.可以看出,尽管均衡器系数初始化为1的位置不同,使得稳态ISI不一致,但均衡器均能收敛. 为验证算法在中等信噪比下的性能,以SAP-UEA算法为例进行如下仿真: 仿真条件同上,信噪比分别设为 15 dB,20 dB,25 dB,经过 6 000 次迭代,纠正相偏后的均衡输出结果如图2所示. 图2 SAP-UEA均衡输出星座图 从图2可以看出,随着信噪比的降低,算法性能逐渐下降.然而,在中等至较高信噪比条件下,能够得到较理想的均衡输出结果. 对自适应算法SAP-UEA与βCMA算法进行比较与分析.信号为8APSK调制的独立同分布信号源,信道仍采用文献[12]中的复信道.图3为剩余ISI随迭代次数的变化曲线.可以看出,SAP-UEA算法相比βCMA算法具有更低的稳态误差,其原因可以从两者的误差函数Φ(yn)及φ(yn)看出.图4为两者的误差函数曲线,其中,γ=2.当 |yn|≫γ时,|Φ(yn)|≫ |φ(yn)|.因此,SAP-UEA算法具有更快的收敛速度;当 |yn|=γ,|Φ(yn)|=0 时,φ(yn)的符号会随机变化,导致βCMA算法的稳态误差较大. 对SAP-UEA算法与SFA算法的性能进行对比.发射信号为独立同分布的16QAM调制信号,信道采用在文献[13-14]所用的复信道,其脉冲响应如图5所示.图6为剩余ISI随迭代次数变化的曲线.可以看出,SAP-UEA算法相比SFA算法的稳态误差更小.这是由于SFA算法采用了均衡器中心抽头系数固定为1的约束所造成的,这种约束在避免代价函数收敛至0的同时,也限制了均衡器系数的调整.而SAP-UEA算法的代价函数对均衡器没有约束,在均衡器系数的更新过程中,都可以使其向最优方向调整. 图3 SAP-UEA与βCMA算法的剩余ISI曲线图4 误差函数曲线 图5 信道的脉冲响应图6 SAP-UEA与SFA算法的剩余ISI曲线 基于向量范数的性质,给出了一种新的无约束盲均衡代价函数.并对代价函数的收敛性,极值点的分布进行了分析和讨论;证明了在无噪声情况下,在代价函数的每个局部最优解处可实现理想均衡,保证了采用随机梯度法迭代时能够使代价函数收敛;并给出了适应不同场合的批数据处理和在线自适应处理两种方法.通过分析和仿真实验说明,该方法在收敛速度和稳态误差等方面优于文献[6-7]中的方法. [1] 赵良, 汪春梅, 孙洪波. 逐幸存序列算法引导的快速盲均衡算法[J]. 西安电子科技大学学报, 2013, 40(2): 201-206. Zhao Liang, Wang Chunmei, Sun Hongbo. Fast Blind Equalization Algorithm Based on PSP[J]. Journal of Xidian University, 2013, 40(2): 201-206. [2] Godard D N. Self-Recovering Equalization and Carrier Tracking in Two-Dimensional Data Communication Systems[J]. IEEE Transactions on Communications, 1980, 28(11): 1867-1875. [3] 李进, 冯大正, 刘文娟. 快速QAM信号多模盲均衡算法[J]. 电子与信息学报, 2013, 35(2): 273-279. Li Jin, Feng Dazheng, Liu Wenjuan. A Fast Multimodulus Blind Equalization Algorithm for QAM Signal[J]. Journal of Electronics & Information Technology, 2013, 35(2): 273-279. [4] Yuan J T, Chao J H, Lin T C. Effect of Channel Noise on Blind Equalization and Carrier Phase Recovery of CMA and MMA[J]. IEEE Transactions on Communications, 2012, 60(11): 3274-3285. [5] Silva M T M, Arenas-Garcia J. A Soft-Switching Blind Equalization Scheme via Convex Combination of Adaptive Filters[J]. IEEE Transactions on Signal Processing, 2013, 61(5): 1171-1182. [6] Shtrom V, Fan H. New Class of Zero-Forcing Cost Functions in Blind Equalization[J]. IEEE Transactions on Signal Processing, 1998, 46(10): 2674-2683. [7] Abrar S, Nandi A K. Adaptive Minimum Entropy Equalization Algorithm[J]. IEEE Communications Letters, 2010, 14(10): 966-968. [8] Shalvi O, Weinstein E. New Criteria for Blind Deconvolution of Nonminimum Phase Systems (Channels)[J]. IEEE Transactions on Information Theory, 1990, 36(2): 312-321. [9] Verbu S, Verdu S, Kenndy R, et al. Convex Cost Functions in Blind Equalization[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1952-1960. [10] Chen M, Tuqan J, Ding Z. A Quadratic Programming Approach to Blind Equalization and Signal Separation[J]. IEEE Transactions on Signal Processing, 2009, 57(6): 2232-2244. [11] Han H D, Ding Z. Steepest Descent Algorithm Implementation for Multichannel Blind Signal Recovery[J]. IET Communications, 2012, 6(18): 3196-3203. [12] Picchi G, Prati G. Blind Equalization and Carrier Recovery Using a ‘Stop-and-Go’ Decision-Directed Algorithm[J]. IEEE Transactions on Communications, 1987, 35(9): 877-887. [13] Kennedy R A, Ding Z. Blind Adaptive Equalizers for Quadrature Amplitude Modulated Communication Systems Based on Convex Cost Functions[J]. Optical Engineering, 1992, 31(6): 1189-1199. [14] Ding Z, Luo Zhiquan. A Fast Linear Programming Algorithm for Blind Equalization[J]. IEEE Transactions on Communications, 2000, 48(9): 1432-1436.


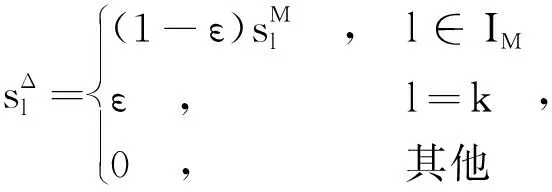

3 算法实现
3.1 批数据处理方法

3.2 在线自适应处理方法
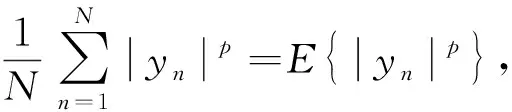
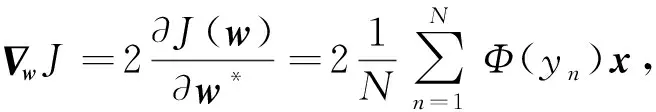

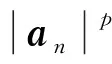
4 仿真与分析
4.1 算法有效性的验证

4.2 与βCMA算法的性能比较
4.3 与SFA算法的性能比较


5 结 束 语

