X信道中一种新的空时编码传输方案
田心记, 逯 静
(河南理工大学 计算机科学与技术学院,河南 焦作 454000)
多输入多输出(MIMO)技术[1]的传输方案分为两类,其一是空间分集方案,其二是空间复用方案.研究较多的空间分集方案是空时分组编码(Space-Time Block Code, STBC)[2-3].STBC获得了分集增益,但是不能获得复用增益.较为理想的编码方案应该能同时获得两种增益,兼顾系统的可靠性和有效性.于是,后来提出了完美空时分组码,其复用增益等于发送天线的个数,并且能实现全分集[4-5].速率为2的空时分组码(Rate 2 Space-Time Block Code, R2-STBC)是完美空时分组码的一种[6].
从系统中所支撑的用户数来划分,MIMO技术可分为单用户MIMO和多用户MIMO,其中,多用户MIMO更加贴近实际的通信系统,是目前关于MIMO技术的研究主流[7-8].每个用户配置多根天线的X信道是一种常见的多用户MIMO系统.MIMO X信道包含两个发送端和两个接收端,每个发送端分别向两个接收端发送信号[9].由于MIMO X信道中两个发送端不可以相互协作,接收端存在严重的多用户干扰,从而影响系统的可靠性[10].
干扰对齐可以使得每个接收端收到的有用信号和干扰信号分别落在不同的向量空间中,从而达到消除MIMO X信道中多用户干扰的目的[11-12].然而,干扰对齐方案的分集增益较低.因此,文献[13]提出了采用空时编码及干扰对齐预编码来消除X信道中的多用户干扰,获得了空时编码带来的分集增益,其可靠性优于相同场景中的干扰对齐方案.然而该方法只适用于每个发送端配置两根天线的X信道.文献[14]将 4×4 的准正交空时分组编码及其预编码引入每个发送端配置多根天线的X信道,通过对空时编码矩阵的每列进行预编码,将每个发送端发送到接收端的信号分别落在不同的向量空间中,消除了多用户干扰,获得了空时编码带来的分集增益.然而,该方法需要反馈信道状态信息或16个N×4 的预编码矩阵(N是接收天线的个数),反馈量较高.

图1 系统模型
为了降低反馈量,笔者提出了每个发送端配置4根天线的X信道中一种新的空时编码传输方案.每个用户采用R2-STBC,首先对编码矩阵进行预编码,然后将预编码后的编码矩阵进行加减组合后分两次发送,通过合理地设计预编码矩阵,使得接收端对接收信号进行线性处理后消除了多用户干扰.与文献[14]相比,所提方案在保持传输效率相同的同时,极大地减少了反馈量.仿真结果显示,误比特率(Bit Error Rate, BER)为10-5时,所提方案获得了不低于 3 dB 的增益.
1 系统模型
系统模型如图1所示.系统包含两个用户和两个接收端Ri(i=1,2),每个用户配置4根天线,每个接收端配置N根天线.Hi是用户1到Ri的信道矩阵,Gi是用户2到Ri的信道矩阵,它们的阶数均为N×4.
两个用户均采用R2-STBC,编码矩阵Ci(i=1,2)和Si分别为
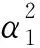
信息的传输分为两个步骤:


其中,N2和W2是噪声矩阵,它们的阶数均为N×2.
所提方案在4个时隙内传输了16个调制符号,其传输效率与文献[14]方案的传输效率相同.
用X1表示R1在两个步骤中接收到的信号之和,即X1=Y1+Y2,用X2表示R2在两个步骤中接收到的信号之差,即X2=Z1-Z2,则
其中,N=N1+N2,W=W1-W2.
由式(5)可看出,对R1的接收信号进行相加运算后消除了C2和S2,而C1和S1相互干扰.由式(6)可看出,对R2的接收信号进行相减运算后消除了C1和S1,而C2和S2相互干扰.即对接收信号进行加减操作后减少了相互干扰的编码矩阵的数量.
接下来,以消除Ci和Si之间的干扰为目标,给出预编码矩阵Ai和Bi的设计方法,i=1,2.
2 预编码矩阵的设计
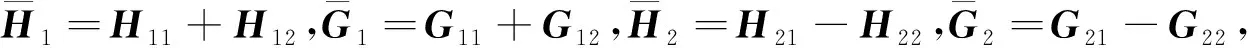
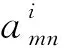
若Ai的第1列和第2列相同且Bi的第1列和第2列也相同,i=1,2,则只需要反馈预编码矩阵的第1列的元素,从而可减少反馈信息.接下来分析是否存在第1列和第2列相同且能消除多用户干扰的预编码矩阵.
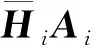
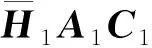
F1和F2的阶数均为2N×4.
根据式(7)、式(11)和式(12)可以得出
(13)

用fm表示F1的各列,m=1,2,3,4,用fk表示F2的各列,k=5,6,7,8.计算可得,fm和fk的内积满足
(20)
方程组(20)包含3个方程、4个未知量,必定有无数组解.
同理,预编码矩阵A2和B2的元素满足方程组(21)时,可消除C2和S2之间的干扰.
(21)
方程组(21)也存在无数组解.
以上的推导表明,存在第1列和第2列相同的预编码矩阵,使得Ci和Si互不干扰,i=1,2,即消除了多用户干扰.所提方案中有4个 2×2 的预编码矩阵,并且预编码矩阵的第1列和第2列相同,因此,只需要反馈每个预编码矩阵的第1列的元素.而文献[14] 的方案需要反馈4个N×4 的信道矩阵或16个N×4 的预编码矩阵,因此所提方案比文献[14]的方案极大地减少了反馈信息.
3 性能分析与比较
不妨假定信道矩阵Hi和Gi的各个元素的实部分量和虚部分量都服从均值为零、方差为σ2的正态分布,i=1,2,噪声为高斯白噪声.在该条件下,等效信道增益越大,系统的可靠性越高.本节比较所提方案与文献[14]方案的等效信道增益.


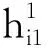
将式(23)和式(24)带入式 (22),可得
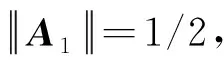


由于等号成立的可能性较小,可以认为E(r2)<16Nσ2.因此,E(r2) (25) 式(25)可以等价为以下两式: 从而R1可以分别译码c和s,即可以分别译码两个用户发送给R1的有用信号.下面以R1为例,给出具体译码过程. 步骤1R1对其接收信号进行相加操作,得到X1=Y1+Y2,然后得到X1的等效表达形式x; R2的译码过程与上述步骤类似. 图2 调制方式为8PSK时两种方案的BER 图2、图3和图4分别给出了调制方式为8PSK、4QAM和16QAM时两种方案的误比特率(BER)曲线.图中的横坐标表示每个用户的信噪比(SNR),M是发送天线的个数,N是接收天线的个数.文献[14]的方案中,M≥5,M=5 时,N≥3,M=6 时,N≥4.为了使得两种方案的发送天线的个数尽量接近,此处只仿真了文献[14]的方案中(M,N)= (5,3)以及(M,N)= (6,4)时的BER曲线.为了具有可比性,对于所提方案,只仿真了(M,N)= (4,3)以及(M,N)= (4,4)时的BER曲线.从图中可以看出,所提方案的BER曲线显著较低.接收天线的个数相同且误码率为10-5时,所提方案的增益均不低于 3 dB. 对于每个用户均配置多根天线的X信道,已有的空时编码传输方案和所提方案都通过发送端预编码以及接收端的非线性处理消除多用户干扰,而所提方案在保持传输效率不变的情况下,极大地减少了反馈信息,并且仿真结果显示,所提方案的可靠性显著优于文献[14]的方案.此外,该空时编码传输方案并非局限于R2-STBC,若每个用户采用其他形式的完美空时分组码,也可用类似的方法得到能消除多用户干扰的预编码矩阵. 图3 调制方式为4QAM时两种方案的BER图4 调制方式为16QAM时两种方案的BER [1] Kaiser T, Zheng F, Dimitrov E. An Overview of Ultra-wide-band Systems with MIMO [J]. Proceedings of the IEEE, 2009, 97(2): 285-312. [2] 张天魁, 程婕, 冯春燕. 一种全速率的多天线中继STBC协作机制[J]. 西安电子科技大学学报, 2010, 37(2): 334-339. Zhang Tiankui, Cheng Jie, Feng Chunyan. Full Rate STBC Cooperation Scheme for the Multi-antenna Relay[J]. Journal of Xidian University, 2010, 37(2): 334-339. [3] Kim Y J, Choi C H, Im G H. Space-time Block Coded Transmission with Phase Feedback for Two-user mimo-mac [C]//IEEE International Conference on Communications. Piscataway: IEEE, 2011: 5963457. [4] Oggier F, Rekaya G, Belfiore J C, et al. Perfect Space-time Block Codes [J]. IEEE Transactions on Information Theory, 2006, 52(9): 3885-3902. [5] Mroueh L, Stephanie R L, Belfiore J C. Application of Perfect Space Time Codes: PEP Bounds and Some Practical Insights [J]. IEEE Transactions on Communications, 2012, 60(3): 747-755. [6] Rabiei P, Al-Dhahir N, Calderbank R. New Rate-2 STBC Design for 2 TX with Reduced-complexity Maximum Likelihood Decoding [J]. IEEE Transactions on Wireless Communications, 2009, 8(4): 1803-1813. [7] Jiang C L, Wang M M, Shu F. Multi-user MIMO with Limited Feedback Using Alternating Codebooks [J]. IEEE Transactions on Communications, 2012, 60(2): 333-338. [8] Wang J T. Joint MMSE Equalization and Power Control for MIMO System under Multi-user Interference [J]. IEEE Communications Letters, 2012, 16(1): 54-56. [9] Maddah-Ali M, Motahari A, Khandani A. Communication over MIMO X Channels: Interference Alignment, Decomposition, and Performance Analysis [J]. IEEE Transactions on Information Theory, 2008, 54(8): 3457-3470. [10] Adrian A, Josep V. Improved Interference Alignment Precoding for the MIMO X Channel [C]//IEEE International Conference on Communications. Piscataway: IEEE, 2011: 5962671. [11] Huang C, Cadambe V R, Jafar S A. Interference Alignment and the Generalized Degrees of Freedom of the X Channel [J]. IEEE Transactions on Information Theory, 2012, 58(8): 5130-5150. [12] Jafar S, Shamal S. Degree of Freedom Region for the Mimo X Channel [J]. IEEE Transactions on Information Theory, 2008, 54(1): 151-170. [13] Li L B, Jafarkhani H, Jafar S A. When Alamouti Codes Meet Interference Alignment: Transmission Schemes for Two-user X Channel [C]//IEEE International Symposium on Information Theory. Piscataway: IEEE, 2011: 2577-2581. [14] Li F, Jafarkhani H. Space-time Processing for X Channels Using Precoders [J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1849-1861.4 复杂度分析与比较
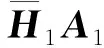


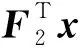
5 仿真结果
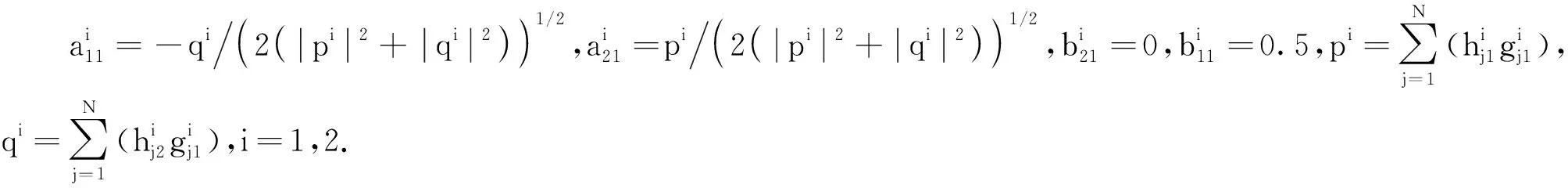

6 总 结


