混合入侵杂草算法用于阵列天线波束赋形
刘 燕, 焦永昌, 张亚明, 王新宽
(1. 西安电子科技大学 天线与微波技术重点实验室,陕西 西安 710071;2. 西北工业大学 电子信息学院,陕西 西安 710129)
阵列天线波束赋形是指通过确定阵列天线的一些参数,使天线阵的辐射方向图尽可能地接近期望的方向图,这是典型的非线性多维数全局优化问题.传统的基于梯度寻优的数值方法大都针对某一类特定的问题,无法对任意波束进行赋形.而智能优化算法不需目标函数导数信息,可以对任意形状的方向图进行设计,因此这类算法,如遗传算法(GA)[1-2]、粒子群算法(PSO)[2-3]和差分进化算法(DE)[4-5]等,成为阵列天线波束赋形的主要方法.
2006年,Mehrabian等[6]提出一种新颖的智能优化算法——入侵杂草算法(Invasive Weed Optimization,IWO).该算法模拟杂草入侵的种子在空间扩散、生长、繁殖和竞争性消亡的过程,原理简单,易于实现,不需要遗传操作算子,具有很强的鲁棒性和自适应性,能简单有效地收敛于问题的最优解.因此,入侵杂草算法一经提出就引起国外天线研究领域学者的关注和研究[7-11].Karimkashi等[7]研究了入侵杂草算法在解决天线问题时的特殊性能表现,通过不同的天线设计实例验证了入侵杂草算法在收敛速度、稳定性等方面均优于粒子群算法和遗传算法.但基本的入侵杂草算法在处理高维数、复杂问题时收敛速度较慢,进化后期容易陷入早熟收敛,因此出现了各种形式的改进入侵杂草算法.比如改变基本入侵杂草算法的非线性调节因子和标准差[8-9],或者把入侵杂草算法与粒子群算法、差分进化算法等其他优化算法相结合[10-11].这些改进后的算法均被应用于对阵列天线进行副瓣降低或深零点生成[8-11],并取得了好的结果.而在实际中,不仅对天线的副瓣有指标要求,很多时候还需要一个具有特殊形状的主瓣,即对主瓣的形状进行设计.正是基于这方面的考虑,笔者用一种全新的思路改进入侵杂草算法,并把该改进算法应用于阵列天线波束赋形的实例中.
在入侵杂草算法中,杂草个体通过一个满足正态分布的标准差独立地散播种子.该标准差的值决定了散播的种子分布在距离杂草多远的距离范围,而且标准差的值随着进化代数的增加而减小.但到进化后期,越来越小的标准差使得产生的新种子分布在距父代杂草很近的范围内,容易陷入局部最优,不利于算法收敛.为了改善该问题,笔者提出一种混合入侵杂草算法(HIWO).首先设计了一个自适应标准差来改进基本的入侵杂草算法,该自适应标准差在随着进化代数的增加而变化的同时,还随每个个体的适应度函数值变化,这样不仅能提高收敛速度,而且还有助于帮助种子跳出局部最优,更好地平衡了全局和局部收敛;然后把简化的二次插值法(Simplified Quadratic Interpolation,SQI)作为一种局部搜索方法嵌入到入侵杂草算法框架中,利用简化的二次插值法较强的局部搜索能力改善算法的整体性能,提高算法的收敛速度和精度.
1 算法描述
1.1 入侵杂草算法基本原理
入侵杂草算法的实现包括4个步骤:初始化、繁殖、空间扩散、竞争性排除.
第1步: 种群初始化.在D维搜索空间,随机产生一组初始解X= (X1,X2,…,XM),其中M为初始种群个数(小于最大种群数Pmax),Xi= (xi1,xi2,…,xiD),i=1,2,…,D,为第i个个体.
第2步: 繁殖.每个杂草个体能够散播的种子数根据其适应度值由最小值到最大值线性变化,越优秀的杂草产生的种子越多.笔者研究的是最小化问题,即适应度值越小的杂草可产生更多的种子:
(1)
其中,f(Xi)为第i个杂草个体的适应度值,Fmax和Fmin为该代进化中最大、最小适应度值,smax和smin为可产生的最大种子数和最小种子数,ffloor(x)函数表示向下取整.
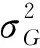
(2)
式中,σinitial和σfinal分别为初始标准差和最终标准差,w为非线性调节因子.由式(2)可以看出,迭代初期较大的σG使得产生的种子分布在距父代较远的范围.迭代后期较小的σG使得产生的种子分布在距父代较近的范围.这样的方式使得算法逐渐完成从全局搜索到局部搜索的转变,有利于提高算法的速度和效率.
第4步: 竞争性排除.当种群数超过最大值Pmax时,所有个体(包括父代和子代)按照其适应度值排序,对排序后的种群从适应度值最小到最大依次选出Pmax个个体,作为该代进化最终保留下来的种群.重复第2步,直到算法满足停止条件.
1.2 自适应标准差
在基本入侵杂草算法中,σG只随进化代数的增加而变小,而在某一代中每个个体的σG值是一样的,这显然不利于算法收敛.在此,笔者设计了一种自适应标准差,使得在某一代中σG的值根据每个个体的适应度值以及该代中最大和最小适应度值进行变化:
(3)
其中,FG,a、FG,max、FG,min分别是该代进化中的平均、最大和最小适应度值;γ为缩放因子,控制标准差的变化范围,一般取0到1之间,这里取值为0.5.
可以看出,对于最小化问题,在某一代中,适应度值小的个体具有较小的标准差,这样有利于种子分布在较优个体周围;而适应度值大的个体标准差较大,有利于在较远范围内分布更优的种子,有助于提高算法的收敛速度.另一方面,该自适应标准差σG,i的取值范围为 [1-γ,1+γ]σG,也就是说,在某一代进化中,所有个体的标准差均在这个范围内变化,不再是一样的值.那么,在进化的下一代某个个体的标准差很可能大于上一代某个个体的标准差,而不是基本入侵杂草算法中下一代所有个体的标准差一定小于上一代所有个体的标准差.尤其是在进化后期,σG的值越来越小,产生的新种子就分布在距父代个体很近的范围内.而采用自适应标准差σG,i后,所有个体的标准差都是变化的,这样有利于使产生的新种子跳出局部最优,在加快收敛速度的同时,有效地平衡了全局和局部搜索能力.
1.3 简化的二次插值法
简化的二次插值法(Simplified Quadratic Interpolation,SQI)是一种简单有效的直接搜索方法.该方法不需要目标函数的导数信息,计算简捷,适合作为启发式搜索算子.简化的二次插值法是一种三点二次插值法,文献[12]将简化的二次插值法与遗传算法结合设计共形天线,得到了比遗传算法更优的结果.文献[13]将简化的二次插值法与差分进化算法结合求解约束优化问题,13个标准测试函数的优化结果显示,与简化的二次插值法结合后的差分进化算法更具优越性.笔者将其作为局部搜索算子,嵌入到入侵杂草算法中,提出一种混合入侵杂草算法(HIWO),以改善算法的局部搜索能力,提高算法的收敛速度和精度.
假设有3个最优个体,Xa=[xa1,xa2,…,xaD],Xb= (xb1,xb2,…,xbD),Xc= (xc1,xc2,…,xcD),其适应度值Fa=f(Xa),Fb=f(Xb),Fc=f(Xc).假设Fb xpi=0.5Ai/Bi,i=1,2,…,D, (4) 在混合入侵杂草算法中,入侵杂草算法作为主要算法进行全局和局部寻优,简化的二次插值法方法作为局部搜索方法嵌入到入侵杂草算法中,以增强整体算法的收敛速度和精度.算法的实现步骤如下. 步骤0: 设置初始参数(如表1所示). 表1 入侵杂草算法和混合入侵杂草算法参数设置 步骤1: 初始化.置G=1,产生初始种群X=(X1,X2,…,XM). 步骤2: 繁殖. (1) 计算所有杂草个体适应度值,并记录最大、最小以及平均适应度值. (2) 用式(1)计算每个杂草个体可以散播的种子数. 步骤3: 空间扩散. (1) 用式(2)和式(3)计算在该代中每个杂草个体的标准差. (2) 每个杂草个体以正态分布的方式散播种子.所有父代个体与其产生的种子一起组成新种群. 步骤4: 竞争性排除. (1) 计算新种群中所有个体的适应度值并由小到大排序. (2) 如果新种群数大于最大种群数Pmax,则根据竞争性生存法则选取种群前Pmax个优秀个体作为保留下来的种群,其余个体被淘汰;否则,转步骤2. 步骤5: 执行简化的二次插值法方法. (1) 从保留下来的种群中依次选择前3个最优个体Xb、Xa和Xc,并计算其适应度值Fb、Fa、Fc. (2) 若Bi≠0,则执行(3);否则, 保持保留下来的种群不变,执行步骤6. (3) 用式(4)计算逼近点Xp=(xp1,xp2,…,xpD),并计算该逼近点的适应度值f(Xp). (4) 若f(Xp) 步骤6: 判断.若满足停止准则,则停止,输出所保留的最好解作为最优解;否则,令G=G+1,转步骤2. 由N个等间距天线单元组成的直线阵,其远场方向图为 (5) 其中,In为第n个阵列单元的复激励电流(包括幅度和相位),d为阵元间的间距,λ为自由空间波长,θ为射线方向与阵轴法线之间的夹角. (6) 为了验证笔者提出算法的有效性,给出两组不同的仿真实例. 实例1 考虑N=50的均匀直线阵,阵元间距d=0.5λ,对激励电流幅度和相位同时优化,以达到期望的方向图(文献[7]中的图5).设计指标:主瓣宽度为20°,主瓣区最大波动不超过 1 dB,副瓣电平低于目标值,每隔0.25°为一个采样点.根据多次实验经验,设定α=0.65,β=0.35. 文献[7]采用基本入侵杂草算法基本上实现了设计目标,虽然文中没有给出优化得到的方向图具体的参数值,但是从文献[7]中的图5可以看出,优化得到的方向图副瓣并没有完全低于期望值,尤其是在靠近主瓣的位置.为了比较混合入侵杂草算法与入侵杂草算法的性能,把这两种算法同时用于求解该问题,两种算法的参数设置与文献[7]保持一致,如表1所示.该问题的维数D为100,两种算法均进化 2 000 代. 由两种算法优化得到的方向图如图1(a)所示.由图1(a)可以看出,入侵杂草算法主瓣区的最大波动为 0.930 5 dB,而混合入侵杂草算法主瓣区的最大波动为 0.512 dB (比入侵杂草算法减少了 0.418 dB);同时,混合入侵杂草算法得到的方向图最高副瓣电平在主瓣区左边为 -25.325 2 dB (而入侵杂草算法得到的值为 -23.947 4 dB),在主瓣区右边为 -20.008 9 dB (入侵杂草算法得到的值为 -17.643 1 dB);并且混合入侵杂草算法得到的方向图主瓣宽度为23.25°,比入侵杂草算法得到的主瓣宽度小0.25°.综合来看,在相同参数设置和进化代数下,混合入侵杂草算法得到了优于基本入侵杂草算法的结果.再来分析两种算法运行20次的平均进化曲线,如图1(b)所示.可以看出,混合入侵杂草算法不仅进化速度高于基本入侵杂草算法,而且在进化后期,入侵杂草算法出现局部收敛的现象得到明显改善,计算精度也明显提高.两种算法优化得到的激励电流幅度和相位见图2. 图1 混合入侵杂草算法与入侵杂草算法方向图和进化曲线对比 图2 混合入侵杂草算法与入侵杂草算法电流幅度和相位对比 实例2 设计指标为: 主瓣宽度为30°(即100°~130°)的余割平方波束和主瓣宽度为100°(即40°~140°)的宽平顶波束.副瓣电平均要求低于 -20 dB,主瓣区最大波动不超过 1 dB,仿真采用16元均匀直线阵,d=0.5λ.经过反复试验,当α=0.55,β=0.45 时,算法可以更好地平衡主瓣区和副瓣区的收敛程度.4种算法均进化 1 000 次,每隔1°为一个采样点,得到的方向图如图3和图4所示,图中黑色虚线为期望方向图的边界.4种算法的优化结果见表2.可以看出,无论是余割平方波束还是平顶波束,在主瓣展宽程度相同或最小的情况下,混合入侵杂草算法得到的方向图在主瓣区均有最小波动值,在副瓣区均有最低的峰值副瓣电平.实例2再次验证了笔者提出的混合入侵杂草算法优于入侵杂草算法及同类其他算法. 图3 4种算法得到的余割平方波束图4 4种算法得到的平顶波束 表2 4种算法的优化结果 针对基本入侵杂草算法在进化后期收敛速度慢、易陷入局部最优的问题,在已有的基本入侵杂草算法的基础上,提出了一种混合入侵杂草算法.该算法先设计了一个自适应标准差,使得算法能更好地平衡其全局和局部收敛能力,在有效克服局部最优问题的同时加快了收敛速度;然后把简化的二次插值法作为局部搜索方法嵌入到入侵杂草算法中,以增强算法整体搜索能力,进一步提高收敛速度和计算精度.通过不同的仿真实例可以看出,笔者所提算法在收敛速度和精度上均优于基本入侵杂草算法及其他同类算法,更适用于天线波束赋形问题,有较高的推广应用价值. [1] Yuan Jiantao, Zhou Hui, Guo Chenjiang, et al. Efficient Optimization of Shaped-beam Sparse Linear Antenna Arrays Using Genetic Algorithm[C]//International Conference on Microwave and Millimeter Wave Technology. Piscataway: IEEE, 2012: 322-325. [2] 刘瑞斌, 鄢泽洪, 孙从武,等. PSO和GA在阵列天线波束赋形中的应用[J]. 西安电子科技大学学报, 2006, 33(5): 797-799. Liu Ruibin, Yan Zehong, Sun Congwu, et al. Application of PSO and GA in Beamforming of an Array Antenna[J]. Journal of Xidian University, 2006, 33(5): 797-799. [3] 王维博, 冯全源. 粒子群算法在阵列天线方向图综合中的应用[J]. 西安电子科技大学学报, 2011, 38(3): 175-180. Wang Weibo, Feng Quanyuan. Application of PSO Algorithm in Pattern Synthesis [J]. Journal of Xidian University, 2011, 38(3): 175-180. [4] Li X, Yin M. Hybrid Differential Evolution with Artificial Bee Colony And Its Application for Design of a Reconfigurable Antenna Array with Discrete Phase Shifters[J]. IET Microwaves, Antennas and Propagation, 2012, 6(14): 1573-1582. [5] Mandal A, Zafar H, Das S, et al. A Modified Differential Evolution Algorithm for Shaped Beam Linear Array Antenna Design[J]. Progress In Electromagnetics Research, 2012, 125: 439-457 [6] Mehrabian A R, Lucas C. A Novel Numerical Optimization Algorithm Inspired from Weed Colonization[J]. Ecological Informatics, 2006, 1(3): 355-366. [7] Karimkashi S, Kishk A A. Invasive Weed Optimization and Its Features in Electromagnetics[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(4): 1269-1278. [8] Roy G G, Das S, Chakraborty P, et al. Design of Non-uniform Circular Antenna Arrays Using a Modified Invasive Weed Optimization Algorithm[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(1):110-118. [9] Basak A, Pal S, Das S, et al. A modified Invasive Weed Optimization Algorithm for Time-modulated Linear Antenna Array Synthesis[C]//IEEE Congress on Evolutionary Computation. Piscataway: IEEE, 2010: 1-8. [10] Hajimirsadeghi H, Lucas C. A Hybrid IWO/PSO Algorithm for Fast and Global Optimization[C]//IEEE EUROCON. Piscataway: IEEE, 2009: 1964-1971. [11] Basak A, Pal S, Das S, et al. Circular Antenna Array Synthesis with a Differential Invasive Weed Optimization Algorithm[C]//10th International Conference on Hybrid Intelligent Systems. Piscataway: IEEE, 2010: 153-158 [12] Xu Zhi, Li Hong, Liu Qizhong, et al. Pattern Synthesis of Conformal Antenna Array by the Hybrid Genetic Algorithm[J]. Progress in Electromagnetics Research, 2008, 79: 75-90. [13] Li Hong, Jiao Yongchang, Zhang Li. Hybrid Differential Evolution with a Simplified Quadratic Approximation for Constrained Optimization Problems[J]. Engineering Optimization, 2011, 43(2): 115-134.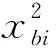
1.4 混合入侵杂草算法的实现步骤
2 阵列天线方向图综合
3 仿真结果
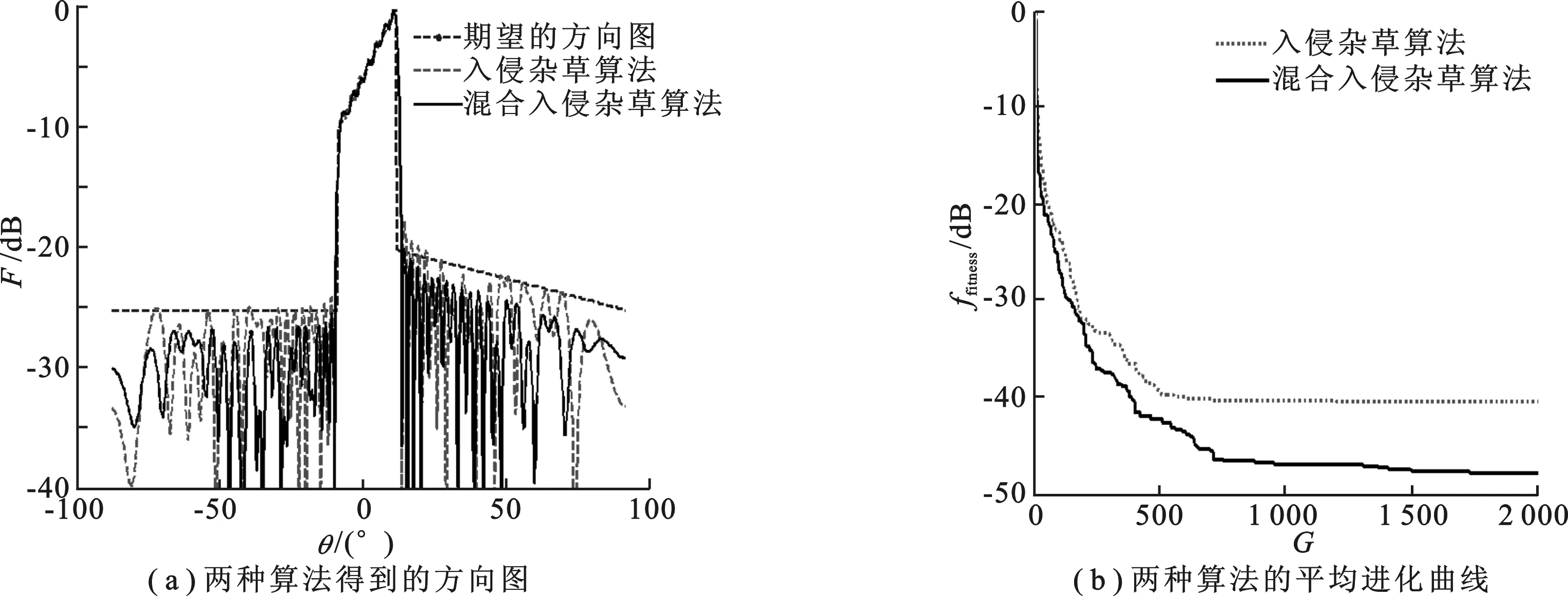
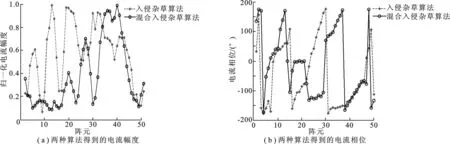
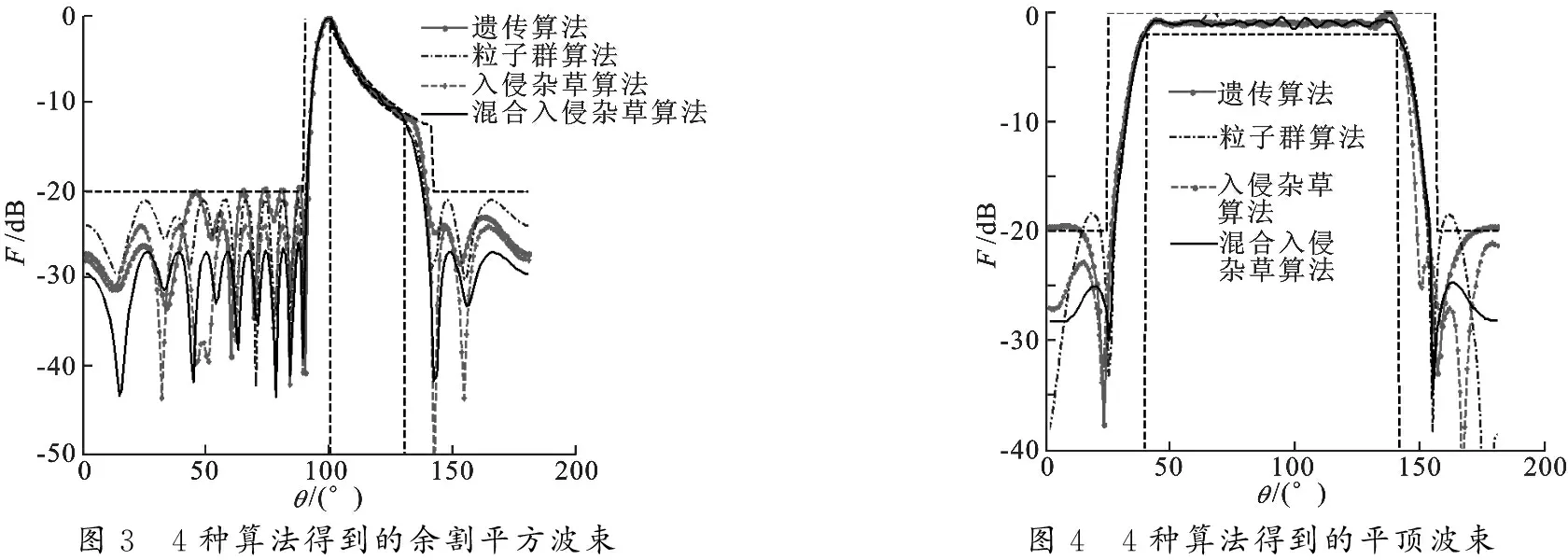
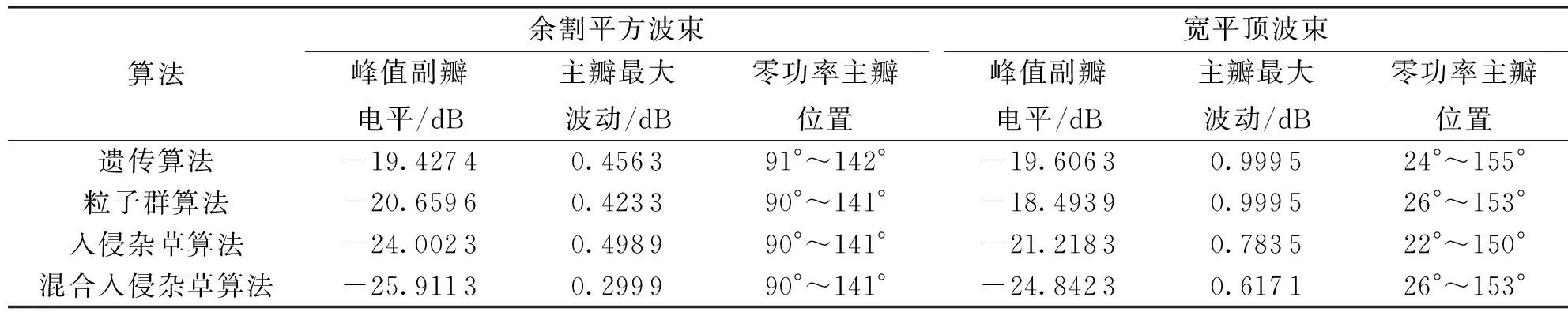
4 总 结

