类电磁优化的片上网络低功耗映射算法

臧明相， 王 婷， 周文宏

(西安电子科技大学 计算机学院，陕西 西安 710071)

片上网络(Network on Chip， NoC)解决了芯片内众多IP核复杂的通信问题．然而，如何实现片上网络的映射才能使功耗最小化的问题正逐渐成为片上网络领域的研究热点[1-3]．在已有的相关研究中大部分采用启发式搜索方法[4]．文献[5]采用蚁群遗传算法来解决负载平衡和低功耗下的片上网络映射问题，通过引入遗传算法来解决蚁群算法对参数过于敏感的问题， 并引入混沌模型来解决算法停滞问题．但算法复杂，所需资源多，效率不高．文献[6]采用混沌遗传算法，克服了遗传算法的早熟现象，可得到更低的通信能耗．但该算法对整个种群的所有个体都实施混沌操作，在一定程度上会破坏优良的遗传基因，有时寻找不到最优解．

类电磁机制算法(Ectromagnetism-like Method，EM)是受电磁场中带电粒子之间的吸引排斥机制启发提出的．该算法将种群中个体看做带电粒子，通过模拟电磁场中带电粒子间的吸引排斥作用引导粒子朝最优解方向移动，具有寻优机理简单、所需资源少、收敛速度快的优点．但其初始种群是通过随机方式生成的，均匀性欠缺；局部搜索中所用的搜索因子是在算法执行前确定的，使得需要提前确定的参数不够精简；而且力的计算过多依赖于粒子间的距离，导致其寻优方向差，效率低[7-13]．

针对原始类电磁算法的以上缺陷，提出了一种改进的类电磁片上网络映射算法(Modified EM MAPping algorithm， MEMMAP)．使用轮盘赌的选择机制[14]进行种群初始化以克服初始粒子质量不均的问题；用调整序进行局部搜索，提高了粒子在局部范围内的精细搜索能力；以目标函数为参数设计电荷计算公式求解合力，用阈值滤掉作用力甚微的粒子，提高计算合力的效率，使之搜索最优解的效率提高．

1 片上网络映射的功耗模型

基于2D Mesh结构片上网络数据传输时的功耗模型一般为

(1)

图1 改进的类电磁片上网络映射算法流程图

2 求解片上网络映射问题的改进类电磁算法

针对片上网络映射问题，对原始类电磁算法中的初始化、局部搜索、电荷及电力的计算方面进行了改进，使之适应于片上网络映射的能耗优化问题．改进的类电磁片上网络映射算法(MEMMAP)基本流程如图1所示．

2.1 基于轮盘赌选择机制的种群初始化

在进行迭代计算之前，需对种群进行初始化，笔者采用实数编码策略．假设有N个IP核，分别为x1，x2，x3，…，xN，映射位置有P个，则初始化每一个粒子为对应的一种随机排列，每一个xi在yi中的位置p表示第i个IP核映射到第p个节点上．第i个粒子yi=x1，x2，…，xi(x1，x2，…，xi为1到N的一种排列)，即IP核x1映射到节点1上，IP核x2映射到节点2上，以此类推，IP核xi映射到节点i上．

在原始的类电磁算法中，其初始种群是通过随机方式生成的，粒子随机性大，全局搜索能力低．因此，笔者提出了一种基于轮盘赌选择机制的初始化方法．

(2)

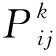
轮盘赌选择的基本过程为：首先计算粒子yk，将Ci映射到Vj的概率看做一个个体；然后根据选择概率的大小把一个圆盘分成大小不同的扇形，扇形大小和选择概率成正比．

(1) 通过旋转轮盘，得出一种对应，即将Ci对应到Vj上，如此循环N次，得出一个完整的映射方案，把这一方案当做粒子yi;

(2) 循环步骤(1)，直到得出m个初始粒子{y1，y2，y3， …，ym}．

利用轮盘赌的初始化方法产生的粒子考虑了降低功耗的目标，初始化得到的粒子比随机方法产生的粒子更加优越，提高了算法的搜索性能，为算法更快、更准确地搜索到全局最优解提供了条件．

2.2 局部搜索

局部搜索旨在为类电磁机制算法提供有效的局部信息，通过在一定范围内搜索比当前粒子更优的粒子，使粒子朝更精确的解移动，进行优化．笔者提出一种利用调整序的思想实现粒子的局部搜索，以提高算法在局部区域精细搜索的能力，通过微型变换粒子，寻找当前粒子附近的最优解．

定义调整算子为Tk(i，j)，表示IP核由位置i调整至位置j，其过程表示为

(3)

调整序为多个调整算子的序列，记为

S=(T1，T2, …,Tk) ．

(4)

为防止算法陷入局部最优，使用门限阈值以在保留粒子多样性的前提下最大限度地减小退化问题．门限阈值D满足

D=f(yl)δ,

(5)

其中，δ为门限选择概率，yl为第l次调整后的粒子，f(yl)为第l次调整后的粒子的目标函数值．当且仅当满足

|f(yl)-f(yl-1)|≤D

(6)

时，新生成的粒子被保留．其中，|f(yl)-f(yl-1)|为新粒子和旧粒子的目标函数之差．

2.3 电荷及电力计算

类电磁算法中电荷的大小与待优化的目标函数值有关．目标函数值较优的粒子电荷较大，反之则较小．基于此考虑，映射粒子yi的电荷量计算为

qi=(fmax-f(yi))/(fmax-fmin) ,

(7)

其中，f(yi)表示粒子yi的目标函数值，fmax和fmin分别表示本代中的目标函数的最大与最小值．从式(7)可以看出，粒子的功耗越小，即目标函数值越小，它所带的电荷量就越大．

对于片上网络的映射优化问题，提出如下的作用力计算公式:

(8)

可以看出，对于当前种群中的任意两个粒子来说，目标函数值较优的粒子吸引目标函数值较差的粒子；反之，目标函数值较差的粒子会排斥另一个粒子．也就是说，两个粒子之间作用力的方向指向其中目标函数值较优的粒子．因此，在对种群中的粒子求合力的过程中，适当地去掉一些对其作用力较小的粒子，对该粒子所受合力总是指向适应度函数值较优的方向这一特点并不会产生很大的影响，却能大大地减少算法的计算量．由此，笔者提出先通过设置阈值过滤掉一部分粒子，再计算合力的方法．阈值的设置公式为

(9)

当粒子yj与粒子yi的距离dij>λi时，粒子yj不参与到yi的合力求和计算中；反之，当粒子yj与粒子yi的距离dij<λi时，粒子yj就参与求合力的计算．这一步的操作简化了求和工作，有助于提高计算合力的效率．

2.4 粒子移动

(10)

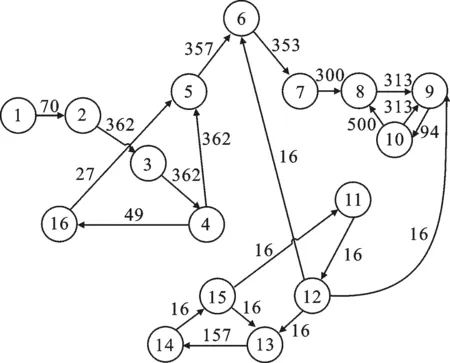
图2 IP核任务特征图APCG

3 仿真与分析

设定4×4的2D-Mesh拓扑结构，采用16核Video Object Plane Decoder(VOPD)的通信核图，如图2所示．任务特征图包含16个子任务，分别由数字1～16表示．每个子任务之间有不同的通信流量，通信方向用箭头表示．

仿真机的CPU为Intel(R)Core(TM)i5，主频为 3.10 GHz、3.09 GHz，内存为 1.82 GB．使用Matlab软件编程完成，并在Linux环境下利用仿真软件Nirgam 2.1仿真．路由算法采用XY路由，最小运行周期为 1 000 个时钟周期，预热阶段设定为5个时钟周期．并且采用恒定比特流，片间隔为2．

图3分别为采用遗传算法、蚁群算法、改进类电磁算法所得映射的功耗分布．由图可见，遗传算法所得的映射功耗大多集中于中间几个节点，而对于四周节点来说，功耗较低．这不利于中间节点的散热．蚁群算法的功耗分布较为均匀，但稳定后的系统平均功耗较大．类电磁算法的功耗趋于平均，且最大功耗也有所减小，系统最终稳定的功耗均小于遗传算法以及蚁群算法．

图3 3种算法所得映射的功耗分布图

图4 通信能耗的对比图

图4为3种算法所生成的映射方案．可以看出，遗传算法容易陷入早熟收敛，效率不高，在 45 s 时才趋于稳定．蚁群算法相比于遗传算法略有提高，在 40 s 左右功耗趋于稳定．而改进的类电磁算法效率更高，在 10～ 30 s 之间，功耗迅速趋于稳定，且最终功耗较小．遗传算法的功耗最终稳定在 10.525 J，蚁群算法的功耗最终稳定在 9.845 J，而改进的类电磁算法所得到的最终稳定功耗仅为 8.745 J，相比之下分别降低了20.35%及12.58%．

4 总 结

笔者采用改进类电磁映射算法解决功耗均衡和低功耗的片上网络映射问题．这种算法通过使用轮盘赌的选择机制进行种群初始化，提高了初始粒子质量；利用调整序方法进行局部搜索，提高了粒子在局部范围内的精细搜索能力；并以目标函数为参数设计电荷计算公式，采用阈值过滤，提高了计算合力的效率．仿真结果表明，在相同的通信任务下，基于改进的类电磁算法不仅能更高效地搜索到映射结果，并且该映射结果能耗分布均匀，平均能耗相对于遗传算法和蚁群算法分别降低了20.35%及12.58%．

[1] 张剑贤, 杨银堂, 周端, 等. 自适应混沌遗传退火的片上网络映射[J]. 北京邮电大学学报, 2011, 34(4): 6-9.

Zhang Jianxian, Yang Yintang, Zhou Duan, et al. NoC Mapping of Adaptive Chaos Genetic Annealing[J]. Journal of Beijing University of Posts and Telecommunications, 2011, 34(4): 6-9.

[2] 杨盛光, 李丽, 高明伦, 等. 面向能耗和延时的NoC映射方法[J]. 电子学报, 2008, 36(5): 937-942.

Yang Shengguang, Li Li, Gao Minglun, et al. An Energy-and Delay-aware Mapping Method of NoC[J]. Acta Electronica Sinica, 2008, 36(5): 937-942.

[3] 宋朝辉, 马光胜, 宋大雷. NoC处理单元随机舍入的启发式应用映射[J]. 计算机辅助设计与图形学学报, 2011, 23(7): 1263-1269.

Song Zhaohui, Ma Guangsheng, Song Dalei. Randomized Rounding Heuristic for Application Mapping to NoC Processing Elements[J]. Journal of Computer-Aided Design and Computer Graphics, 2011, 23(7): 1263-1269.

[4] 张剑贤, 周端, 杨银堂, 等. 一种低能耗的片上网络映射算法[J]. 西安电子科技大学学报, 2011, 38(4): 95-100.

Zhang Jianxian, Zhou Duan, Yang Yintang, et al. Low Energy Consumption Mapping Algorithm for the Network-on-chip[J]. Journal of Xidian University, 2011, 38(4): 95-100.

[5] 易伟, 王佳文, 潘红兵, 等. 基于蚁群混沌遗传算法的片上网络映射[J]. 电子学报, 2011, 39(8): 1832-1836.

Yi Wei, Wang Jiawen, Pan Hongbing, et al. Ant Colony Chaos Genetic Algorithm for Mapping Task Graphs to a Network on Chip[J]. Acta Electronica Sinica, 2011, 39(8): 1832-1836.

[6] Moein-Darbari F, Khademzade A, Gharooni-Fard G. CGMAP: a New Approach to Network-on-Chip Mapping Problem [J]. IEICE Electronics Express, 2009, 6(1): 27-34.

[7] Birbill S, Fang Shucherng. An Electromagnetism-like Mechanism for Global Optimization[J]. Journal of Global Optimization, 2003, 25(3): 263-282.

[8] 姜建国, 龙秀萍, 田旻, 等. 一种基于佳点集的类电磁机制算法[J]. 西安电子科技大学学报, 2011, 38(6): 167-172.

Jiang Jianguo, Long Xiuping, Tian Min, et al. Electromagnetism-like Mechanism Algorithm based on the Good Point Set[J]. Journal of Xidian University, 2011, 38(6): 167-172.

[9] Kaelo P, Ali M M. Differential Evolution Algorithms Using Hybrid Mutation[J]. Computation Optimum Application, 2007, 37(2): 231-246.

[10] 王晓娟, 高亮, 陈亚洲. 类电磁机制算法及其应用[J]. 计算机应用研究, 2006, 26(3): 67-70.

Wang Xiaojuan, Gao Liang, Chen Yazhou. Electromagnetism-like Mechanism with Its Application[J]. Journal of Computer Applications, 2006, 26(3): 67-70.

[11] 韩丽霞, 王宇平. 求解无约束优化问题的类电磁机制算法[J]. 电子学报, 2009, 37(3): 664-668.

Han Lixia, Wang Yuping. Electromagnetism-like Mechanism Algorithm for Unconstrained Optimization Problem[J]. Acta Electronica Sinica, 2009, 37(3): 664-668.

[12] 杨晓凌, 邱涤珊, 彭黎, 等. 改进类电磁算法在武器目标分配问题中的应用[J]. 国防科技大学学报, 2011, 33(6): 150-153.

Yang Xiaoling, Qiu Dishan, Peng Li, et al. Application of Modified Electromagnetism-like Algorithm in Weapon-target Assignment Problem[J]. Journal of National University of Defense Technology, 2011, 33(6): 150-153.

[13] 姜建国, 王双记, 刘永青, 等. 一种实用的类电磁机制算法[J]. 西安电子科技大学学报, 2013, 40(2): 48-53.

Jiang Jianguo, Wang Shuangji, Liu Yongqing, et al. Practical Electromagnetism-like Mechanism Algorithm[J]. Journal of Xidian University, 2013, 40(2): 48-53.

[14] 王芳, 邱玉辉. 一种引入轮盘赌选择算子的混合粒子群算法[J]. 西南师范大学学报, 2006, 31(3): 93-96.

Wang Fang, Qiu Yuhui. A Hybrid Particle Swarm Algorithm with Roulette Selection Operator[J]. Journal of Southwest China Normal University, 2006, 31(3): 93-96.