合成孔径雷达目标特征提取新方法

段 佳， 张 磊， 邢孟道， 梁 毅

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

合成孔径雷达(Synthetic Aperture Radar， SAR)目标的散射中心特征参数提取是目标特性分析与识别领域的热点问题．通常而言，散射中心参数的估计依赖于散射中心模型的合理性．近年来，国内外学者针对传统的点散射模型分辨率受限等问题，先后提出了指数衰减模型[1]、几何绕射模型[2]和属性散射中心模型[3]．其中，属性散射中心模型从几何绕射解和物理光学的角度出发，用一组简洁的参数来描述典型结构的电磁和几何特性信息，有效地压缩了数据量．较之另两种模型，它更能反映目标的真实物理散射含义．若能基于此模型进行特征参数提取和成像，有望增强雷达图像的可视性．但其模型参数维度高，估计困难．

对合成孔径目标的属性散射中心特征提取的方法相对较少．初期提出的频率域直接提取参数的方法，对所有参数同时估计，效率低，只适用于少量散射中心的雷达图像[4]．为提高效率，俄亥俄大学提出先对目标图像运用分水岭算法分割，然后对含有少量散射中心的子图像进行最大似然估计，在提高参数估计效率的同时也克服了不同散射中心参数估计过程中的相互干扰．但分割后的属性散射中心图像，虽各子块的散射中心总数下降，维度依然高，运算量依然较大．为此，笔者通过简化属性散射中心模型构造表征字典并引入快速傅里叶变换实现散射中心位置估计．最后利用RELAX对各属性散射中心迭代提取来提高算法的运算效率．

1 简化的属性散射中心参数化模型

假设散射中心p的回波数据Sp(f,φ)满足属性散射中心模型[3]:

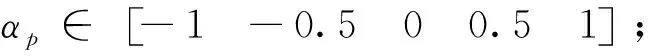
(2)

可见，局部式散射中心可看成展布式散射中心的特例．因此，只讨论展布式散射中心模型参数估计．

2 属性散射中心模型参数估计

2.1 展布式散射中心模型参数估计

设雷达目标回波含多个属性散射中心，则回波信号为

(3)

其中，S(f,φ)表示雷达目标总回波信号；e(f,φ)为杂波和噪声，假设服从高斯分布．

传统RELAX算法是基于信号分析理论[7- 8]的，其基本思想为:利用已估计的p个散射中心的参数重构对应信号，并在原始信号上减去已重构的p个信号构造剩余信号，利用剩余信号估计散射中心p+1 的参数，再利用散射中心p+1 的参数重新对前p个信号的参数进行估计，重复迭代至收敛．首先，令

(4)

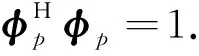
(5)

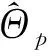
(6)

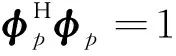
(7)

其中，⊙为汉德蒙德乘．若能得到其他参数的估计值，则可用式(7)求解幅度估计．将式(7)代入式(6)，亦可得其他参数的估计，即找到使φp与Sp内积最大的参数集:

(8)

若直接利用上述方法对参数{Lp，φp，xp，yp}联合估计，参数维度大，运算效率低．例如，假设每一维参数搜索30点，搜索的循环次数便为 8.1×105．引入快速傅里叶变换实现算法的快速化．注意到式(2)中位置参数项在小角度下是傅里叶基表示形式，因此，可利用快速傅里叶变换估计位置．该方法操作很简单，只需对信号在频率角度域补零插值，再进行逆傅里叶变换便可以实现对位置的估计，其中补零是为了提高位置参数的估计精度．将位置参数估计值代入φp，得只有二维参数的φp0，即

再利用式(10)对长度和初始角度进行二维联合估计．这样便将参数维数降低，运算效率提高．

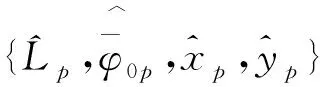
(11)

在剩余信号中减去重构信号p，可更新剩余信号[8]为

(12)

其中，初始化sRe 1(f,φ)=S(f,φ)．再对sRe p+1(f,φ)重复上述操作，迭代至收敛．

综上，基于RELAX的展布式散射中心模型参数估计算法流程如下．

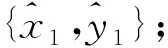
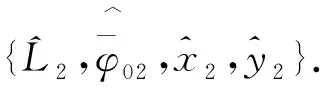
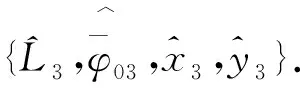
重复上述操作，迭代至p等于指定信号的个数．

2.2 搜索栅格分析

运用上述方法进行长度和初始指向角度估计时，搜索角度、长度间隔会直接影响估计结果．当搜索间隔太大时，有可能跳过sinc函数主瓣，导致严重偏差．因此，有必要对搜索间隔进行讨论．

(1) 长度搜索间隔．假设其他参数估计准确，而长度存在偏差ΔL．此时，归一化的误差信号可写成

(13)

若长度误差在最大频率处满足最小误差要求，则在其他频率处必满足．对最大频率下的信号逆傅里叶变换为

(14)

(15)

其中，Δφ为方位积累角，ρx为方位分辨率．

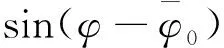
其中，ρy为距离分辨率．综上，长度估计误差满足

(18)

则不会出现偏差较大的情况．需指出，由于长度误差只影响幅度，故敏感性不强．式(17)是充分条件，可适当放宽提高效率．

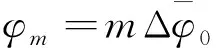
(19)

计算其与真实信号的相关系数，找到使相关系数取最大的角度．

相关函数定义为两个信号在时域的卷积，时域的卷积等于各自逆傅里叶变换的共轭乘积在0时刻的值．对γ的逆傅里叶变换为

(20)

可以看出，角度误差影响信号的相位，因此笔者提出的方法对角度采样敏感．计算最小波长处，γ与真实信号的相关函数:

(21)

可知，对φm采样要能无失真恢复出相关函数，则要求其采样带宽大于相关函数的带宽，如式(21)．

2.3 角度搜索范围

若无先验信息，对180°角度搜索，运算量庞大．因此，有必要对角度搜索范围进行讨论．由式(2)可知，某散射中心要能在回波中表现，其幅度调制项必有一部分落在sinc函数的主瓣内，即 ∃φ使

(22)

(23)

若L=0，sinc幅度调制项为1，与初始指向角度无关；其他L则按式(23)计算相应角度范围．

3 实验结果与分析

3.1 参数估计验证的电磁仿真实验

雷达采用阶跃扫频模式，起始工作频率为 8.5 GHz，终止频率为 9.5 GHz，步长为 10 MHz，HH极化，目标距离为 20 m，高度为 7 m，俯仰角为0°，起始目标方位角为87.5°，终止方位角度为92.5°，方位角速度为0.05°/s．仿真目标属性参数如表1所示．在此参数及不同频率依赖因子αp下，(B/fc)αp差别最大为2%，因此可忽略频率依赖因子．由于位置参数的估计与点散射模型一致，只考查幅度调制项上参数的估计精度．利用上述参数仿真，距离-多普勒(Range-Doppler， RD)成像结果如图1(a)和(b)所示．可以看出，两个散射中心相互混叠形成很多强弱交替的目标，很难从图像判断目标组成．运用笔者提出的方法进行参数估计与信号提取，通过两次迭代提取的信号和总信号的距离-多普勒成像分别如图1(c)～(e)所示，估计参数如表1所示．此时，残余信号的距离-多普勒成像结果如 图1(f) 所示，计算残余能量与原始能量比为 1.385 4×10-12．

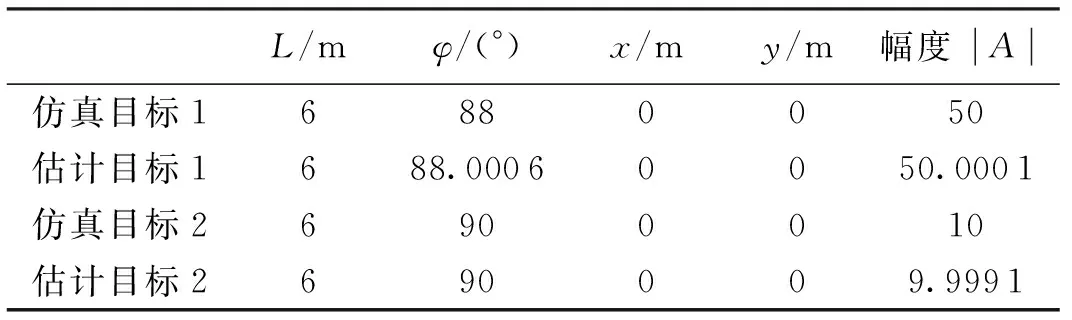
表1 仿真与估计目标参数

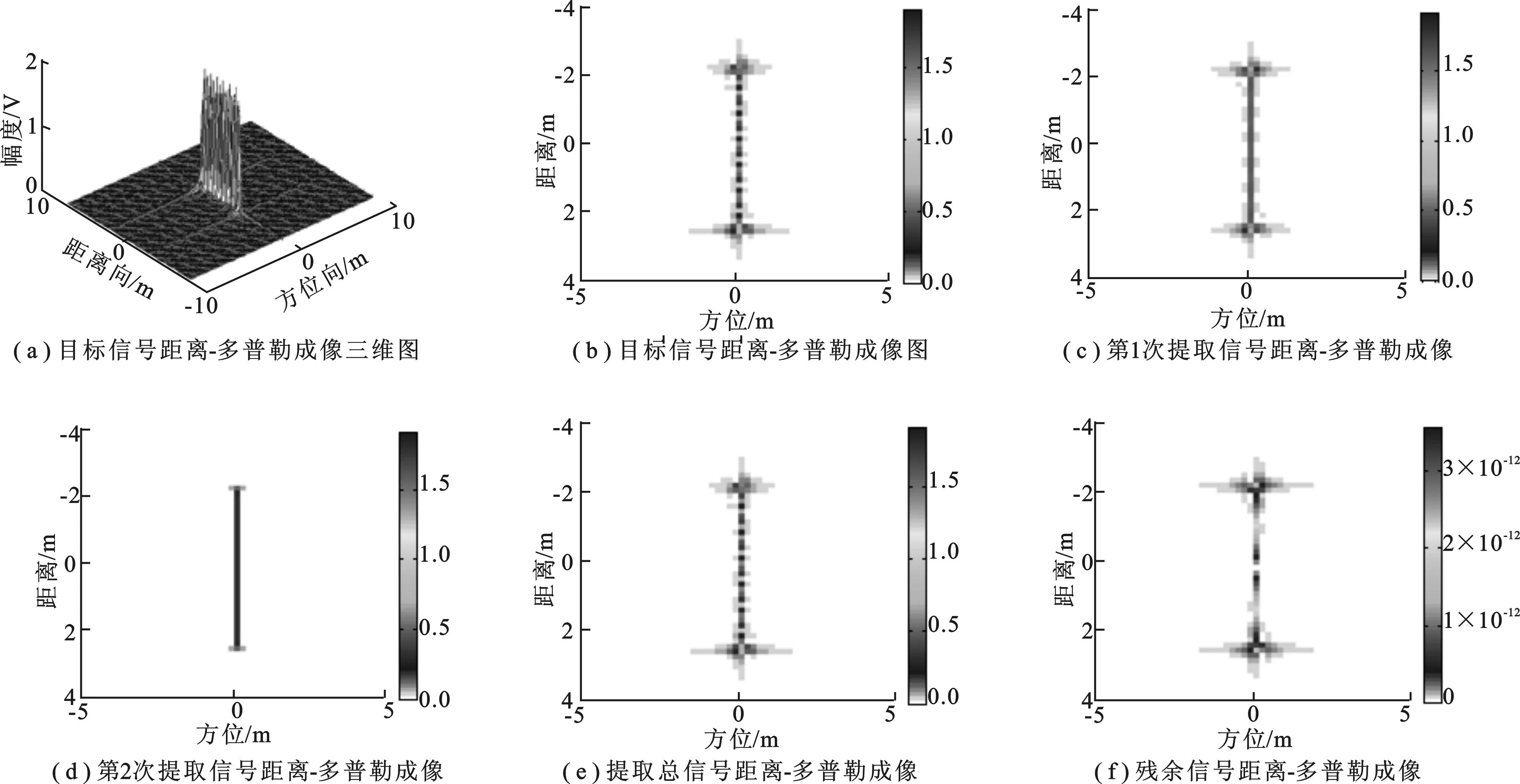
图1 RELAX提取信号

在主频为3.2 GHz和3.19 GHz的i5双核CPU、内存4 GB条件下，采用笔者提出的方法和文献[4]中的方法估计参数，耗时分别为 17.4 s 和 1 821 s．利用文献[4]估得目标1长为 6 m，初始指向88°，位置(0，0)，幅度为 50.000 1；目标2长为 6.2 m，初始指向90°，位置(0，0)，幅度为 10.112 1．可看出：笔者提出的方法在提高运算效率的同时，也未损失参数估计精度．这是由于笔者提出的方法通过引入快速傅里叶变换对属性散射中心的位置参数进行估计，将文献[4]中的四维参数联合估计问题降维，算法复杂度大幅度下降．同时，快速傅里叶变换也保证了位置参数估计的精度．

在不同信噪比下进行50次蒙特卡洛实验，计算估计参数的均方误差根(Root of Mean Square Error， RMSE)随信噪比(Signal-to-Noise Ratio， SNR)变化曲线如图2所示．

(24)

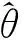
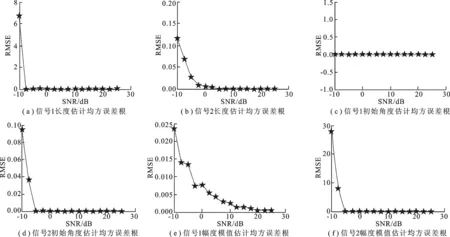
图2 参数估计均方误差根随信噪比变化曲线

由图2可知，笔者提出的方法参数估计精度高，对噪声较不敏感，稳健性高．幅度估计在信噪比高于 0 dB 时，能取得较好的效果；在信噪比低于 0 dB 时，受噪声影响，幅度估计的均方根误差远大于1，这是不可避免的．

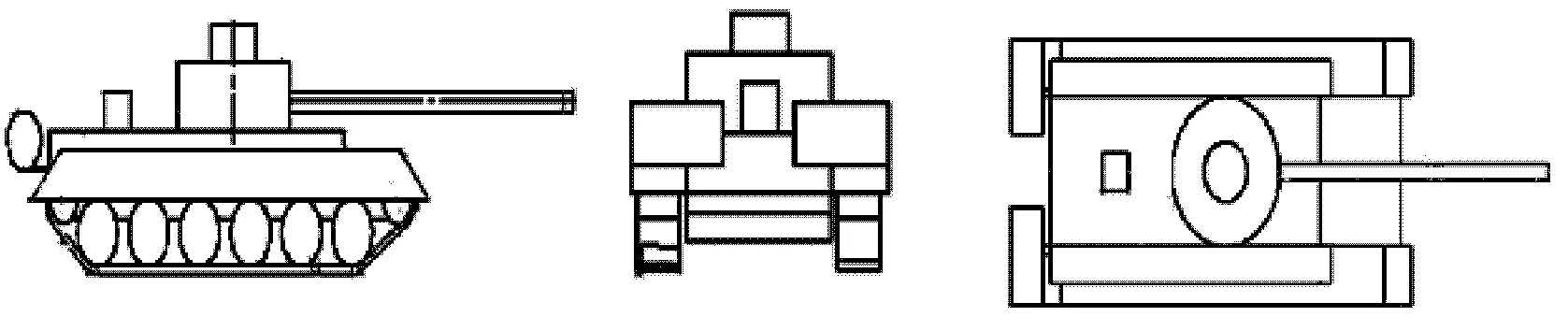
图3 坦克模型

3.2 复杂散射模型的信号提取

首先使用仿真的坦克模型(如图3所示)，雷达为阶跃扫频模式，频率范围为 8.5～ 9.5 GHz，步长为 10 MHz，方位角在 87.5°～ 92.5°区间，方位角速度为 0.05°/s．由先验信息取长度搜索范围为 0～ 6 m，角度搜索范围为 87°～ 93°，采样间隔分别为0.16°和 0.045 m，满足式(17)和式(21)．对原始数据距离多普勒成像如图4(a)所示；采取笔者提出的算法提取参数，重建信号与残余信号距离多普勒成像结果如图4(b)和(c)所示．由于散射中心点数多，不能定量分析参数估计精度，故从信号能量方面定性分析[3]．通过计算，残余信号与原始信号能量比为15.43%，间接说明笔者提出的方法的有效性．

图4 RELAX提取坦克数据

将笔者提出的方法与传统基于点散射模型的信号提取方法进行对比．在残余能量比为5%的终止条件下，笔者提出的方法仅用22次迭代，而基于点散射模型用了106次．利用笔者提出的方法可以在重建信号的同时提取目标的尺寸，如图4(b)所示，这是基于点散射模型的信号提取不具备的，即提取的参数可表述典型结构两种方法，提取信号和残差信号的距离-多普勒成像结果如图4(c)～(f)所示．通过对比基于点散射中心重构的炮杆与基于属性散射中心重构的炮杆(椭圆标记处)，可看出基于属性散射中心重构炮杆更接近原始炮杆；此外，基于属性散射中心的残余信号能量要弱于基于点散射中心的残余信号能量．用更少的迭代次数重构更完整的信号，并同时提取目标的几何尺寸，这是笔者提出的方法相比基于点散射模型信号提取方法的优势．

对XPATCH挖掘机数据进行参数估计和信号提取．方位观测角范围为 -7.428 6°～ -1.642 9°，采样间隔为 0.071 4°；频率观测范围为 7.047 2～ 8.51 5 GHz，采样间隔为 11.557 MHz．长度搜索范围为 0～ 6 m，间隔为 0.1 m；角度搜索间隔为0.18°．原始信号距离-多普勒成像、重构信号距离-多普勒成像和残余信号距离-多普勒成像结果如图5所示．可以看出，重构信号能较完整地反映原始信号的结构．利用重构信号的能量定性地分析笔者提出的算法，残余信号与原始信号能量比为7.21%，从而间接验证了笔者提出的方法对信号的参数提取的准确性．

图5 RELAX提取挖掘机数据

4 总 结

由于属性散射中心模型对面、线结构描述更为贴切，笔者提出了一种快速属性散射中心模型参数估计方法．针对传统算法运算效率低的问题，通过模型简化、快速傅里叶变换以及参数解耦来提高效率．利用属性参数可重构信号．实验验证了该方法的有效性．

[1] Gerry M J, Potter L C, Gupta J I, et al. Parametric Model for Synthetic Aperture Radar Measurements [J]. IEEE Transactions on Antennas and Propagation, 1999, 47 (7): 1179-1188.

[2] Koets M A, Moses R L. Feature Extraction Using Attributed Scattering Center Models on SAR Imagery [C]//Proceedings of SPIE: 3721. Bellingham: SPIE, 1999: 104-115.

[3] Xu S K, Wei X Z, LI X, et al. Parameter Estimation and Performance Analysis of Coherent Polarization Attributed Scattering Center Model[J]. Chinese Journal of Electronics, 2013, 22(1): 195-201.

[4] Ai F Z, Zhou J X, Hu L, et al. The Parametric Model of Non-uniformly Distributed Scattering Centers [C]//IET International Conference on Radar Systems. Stevenage: IET, 2012: 16-20.

[5] 唐涛, 粟毅. 散射中心特征序贯匹配的SAR图像目标识别方法[J]. 系统工程与电子技术, 2012, 34(6): 1131-1135.

Tang Tao, Su Yi. Object Recognition in SAR Imagery Using Sequential Feature [J]. Systems Engineering and Electronics, 2012, 34(6):1131-1135.

[6] 段佳, 张磊, 盛佳恋, 等. 独立属性散射中心参数降耦合估计方法[J]. 电子与信息学报, 2012, 34(8): 1853-1859.

Duan Jia, Zhang Lei, Sheng Jialian, et al. Parameter Decouple and Estimation of Independent Attributed Scattering Centers[J]. Journal of Electronics & Infomation Technology, 2012, 34(8): 1853-1859.

[7] Jiao Yun, Yu Jizhou, Che Renquan. Application of RELAX Algorithm to ISAR Superresolution Imaging[C]//Proceedings of CIE International Conference on Radar. Piscataway: IEEE, 2006: 4148310.

[8] 邵朝, 保铮. RELAX算法的相关域分析[J]. 西安电子科技大学学报,1997, 24(2): 164-171.

Shao Chao, Bao Zheng. The Analysis of Correlated Domain of the RELAX Algorithm[J]. Journal of Xidian University, 1997, 24(2): 164-171.