复杂铸造工艺装配体有限元网格划分关键技术研究

陈 涛，廖敦明，庞盛永，周建新

（华中科技大学材料成形与模具技术国家重点实验室，湖北 武汉 430074）

在计算机技术飞速发展的今天，铸造这个古老的行业也开始引进先进的信息化和智能化技术，对传统的铸造工艺设计和生产过程进行现代化和信息化改造。在计算机数值计算的基础上，学者们发展出了铸造CAE 技术[1]。铸造CAE 技术将传统的试错法放在计算机虚拟的世界中进行，大大减少了产品试制周期和成本，提高生产效率，并能减少对经验的依赖，及时发现可能的铸造缺陷，根据观测到的缺陷成因优化铸造工艺参数，提高铸件成形质量，在实际的铸造生产实践中直接生产出合格的产品[2]。

铸造CAE 技术中采用的主要方法包括有限差分法和有限元法，其中有限差分法多用于铸造过程的充型和凝固模拟，有限元法更适合于铸造过程的热应力模拟。有限差分法由于所用的有限差分网格生成方便简单，在铸造企业中的应用比较广泛。而有限元法所涉及的有限元网格划分要复杂许多，特别是对于复杂铸造工艺装配体几何模型，有限元网格很可能无法顺利生成，造成后续的有限元计算分析不能正常进行，严重制约了有限元法铸造CAE 技术的推广和应用。许多企业花大价钱买来的有限元法铸造CAE 软件常常束之高阁，没能很好地应用起来，为企业创造价值。

在铸造CAE 中，大多使用的几何模型采用Stereolithography（STL）格式，用许多三角形来描述几何模型的表面。对于传统用于计算流动和传热的有限差分法来说，目前已经有非常成熟稳健的有限差分网格划分算法。但对于有限元方法，有限元网格对几何模型的准确性要求比有限差分网格高许多，一些STL 几何模型中的错误会导致有限元网格划分失败。如图1 所示，常见的STL 几何模型中的错误有如下几种[3]：a）三角形退化成线段或点；b）超过三个三角形共有一条边，构成非流形；c）三角形相互重叠和交错；d）三角形空缺形成孔洞。

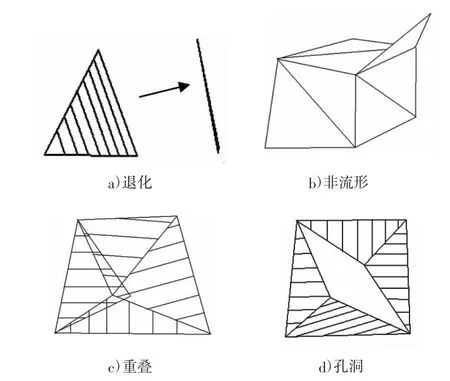
图1 常见的STL 几何模型中的错误

铸造工艺常常由许多部分组合而成，如铸件、浇道、冒口等，导入铸造CAE 分析中的几何模型常常是装配体。装配体中出现的表面接触和体积相交等几何特征对有限元网格划分也是一大考验[4-6]。

为了实现有限元网格划分的自动化和智能化，让操作人员专注工艺设计而不是几何错误修复和网格划分的细节问题，本文提出一种自动对STL 装配体进行有限元四面体网格划分的算法。此算法能够根据导入的STL 几何模型装配体的几何特征，自动修复或忽略大部分STL 几何模型中的错误，智能地处理装配体中的表面接触和相交体积的几何特征，自适应地选择合适尺寸的四面体单元划分整个装配体，不需要人为的参数设置和网格手动修复，最终得到质量优良并保持几何一致性的四面体有限元网格，可以用于后续的有限元热应力数值模拟。

1 复杂铸造工艺装配体有限元网格划分关键技术

本文提出的有限元网格生成方法包括隐式曲面几何描述方法、有限元网格尺寸计算方法，以及有限元网格生成和网格质量优化方法等三个部分，下面将一一进行详述。

1.1 隐式曲面几何描述方法

由于导入的铸造工艺STL 装配体中会带有一些错误，本文采用隐式曲面这种更稳健的几何描述方式来表示几何模型的表面，自动消除或忽略STL装配体的错误，为有限元网格划分提供准确的几何模型表面信息。

STL 文件格式是一种用三角形集合显式描述几何模型的方法，只包含模型表面的几何信息。相对于STL 文件格式，隐式曲面是用三维空间中某个函数的等值面隐式描述几何模型的方法，除了模型表面的几何信息，它还包含了整个空间范围内的几何信息。

为了方便起见，通常选用带符号距离函数的零值面作为隐式曲面，这样也不失一般性。式（1）为带符号距离函数φ（x）的定义[7，8]：

其中，Ω+为几何模型外的区域，Ω-为几何模型内的区域，∂Ω 为几何模型的表面，d（x）表示空间任一点x 到几何模型表面∂Ω 最小距离的函数。式（2）为d（x）的表达式：

与STL 文件格式相比，隐式曲面描述几何模型有下列几个特点：

1）用隐式曲面描述几何模型，不会存在任何显示格式中的错误。将STL 装配体转换成隐式曲面描述，许多STL 文件中的错误会自动消除。

2）通过隐式曲面，许多几何模型的重要几何信息能够容易地计算得到。

3）铸造工艺装配体的各个部分可以容易地通过隐式曲面进行布尔运算。

4）隐式曲面表示的几何模型表面总是连续可微的，原几何模型中所有轮廓边和特征顶点都会圆滑过渡。该特性符合实际铸件的工艺特征。

1.2 有限元网格尺寸计算方法

有限元网格划分算法生成的有限元网格需要有合适的单元尺寸，网格尺寸过大则计算精度不高，甚至导致网格划分失败，网格尺寸过小又会造成计算量过大。如何设置合适的单元尺寸，对于操作人员来说也是一件繁琐麻烦的任务。

本文提出一种自适应网格尺寸的智能化计算方法，网格尺寸函数fh（x）的表达式如下式所示：

其中a，b，c 为权系数，φ厚度（x）为模型的厚度分布函数，h用户（x）为用户自定义的网格尺寸分布函数，k（x）为模型的表面曲率，∂Ω 为模型表面，∂ΩSF为模型的轮廓边等重要几何特征。

该方法根据计算得到的几何模型大致厚度与表面曲率设置网格尺寸函数，得到的网格尺寸函数分布自动满足单元尺寸的几何自适应要求，可以不需要操作人员费时费力的手动设置。如果操作人员对于网格尺寸有特殊的要求，也可以方便地进行设置，让指定位置的网格尺寸与设定值近似。

1.3 有限元网格生成和网格质量优化方法

由于铸造工艺装配体几何模型采用隐式曲面方法描述，本文也相应地采用基于隐式曲面的有限元网格划分和优化方法，其整体流程如图2 所示：a）导入STL 几何模型；b）变换为隐式曲面几何描述；c）根据几何特征自动计算合适的网格尺寸函数；d）在隐式曲面包含的内部空间中根据网格尺寸要求撒布合适的顶点并连接成四面体凸包；e）去除隐式曲面外部空间中的四面体，形成初始有限元四面体网格；f）优化网格质量和表面一致性得到最终有限元四面体网格。

图2 隐式曲面有限元网格划分和优化算法流程

2 应用实例

基于本文提出的有限元网格划分方法，开发了有限元四面体网格划分前处理模块。下面将用两个实际生产的铸件几何模型测试本文的有限元网格划分方法。

2.1 发动机缸体铸件

第一个例子是一个实际生产的发动机缸体铸件的几何模型。图3 为发动机缸体铸件的STL 几何模型，可以看到此STL 模型由910，644 个三角形来表达发动机缸体铸件的复杂几何形状，包括复杂的凸台、凹槽、孔洞及内腔等。图4 为带轮廓边显示的发动机缸体铸件的几何模型及局部放大图。由于几何模型复杂，图中显示的黑色轮廓边（断续线段）数量较多，从局部放大图可以看到有一些错误判断的轮廓边，这说明STL 几何模型中带有一些小到肉眼很难发现的几何错误，如三角形退化、三角形丢失、非流形连接等。目前大多商品化有限元网格划分软件（例如ProCAST，HyperMesh，ICEM 等）都无法顺利为此发动机缸体铸件STL 几何模型生成合格的有限元网格。

图3 发动机缸体铸件的STL 几何模型

图4 带轮廓边显示的发动机缸体铸件的几何模型及局部放大图

图5 显示渲染了网格尺寸函数的发动机缸体隐式曲面，从图5 可见，虽然发动机缸体铸件的几何模型非常复杂而且带有一些几何错误，本文提出的有限元网格划分方法仍然可以生成正确的隐式曲面及网格尺寸函数，并最终得到合格的有限元网格，如图6 所示。从有限元网格的全视图和剖视图可见，生成的有限元网格与原几何模型有良好的几何一致性。从图7 的最终有限元网格质量分布图中可以看到，本文提出的复杂铸造工艺有限元网格划分方法所生成的整体网格有优良的网格质量，质量超过0.8 的高质量单元大约占总单元数的65%，质量低于0.1 的低质量单元仅有20 个。

图5 渲染了网格尺寸函数的发动机缸体隐式曲面

图 6 发动机缸体铸件的有限元网格及剖视图

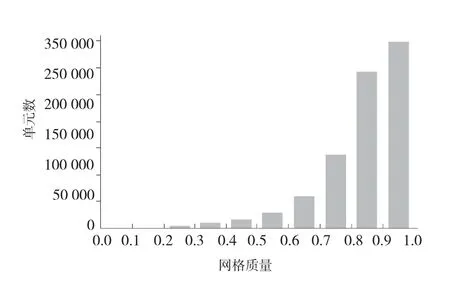
图7 发动机缸体铸件有限元网格的最终单元质量分布

2.2 发动机缸体铸件

第二个实例是一个数控机床横梁铸件的铸造工艺方案如图8 所示，由几个部分装配组成：铸件、冒口、浇道、浇注入口、冷铁。此数控机床横梁铸件属于大型薄壁复杂铸件，其总长为10.937 m，从剖视图中可以见到横梁铸件内腔最薄壁厚仅为20 mm.总长与最薄壁厚之比超过500，这会对有限元网格的划分造成一定的困难，最终生成的单元数会比较多。该铸造工艺装配体的STL 几何模型同样无法用现有的商品化网格划分软件生成合格的有限元网格。

图8 数控机床横梁铸件的铸造工艺图及其剖视图

图9 为数控机床横梁铸件铸造工艺的STL 几何模型装配体，其中横梁铸件、浇道、冒口、冷铁和浇注入口的STL 模型的三角形个数分别为455，780、9890、31548、3948 和960.STL 模型中的三角形个数可以反映模型几何特征的复杂程度，虽然横梁铸件STL 模型的三角形个数没有前面发动机缸体铸件的多，但加上浇道和冒口等浇注工艺时，整个装配体的几何特征变得更加复杂。

图9 数控机床横梁铸件铸造工艺的STL 几何模型装配体

图10 显示了渲染了网格尺寸函数的数控机床横梁铸件的隐式曲面。可以看到，本文提出的有限元网格划分算法能够为复杂的几何模型装配体生成与原几何模型一致的隐式曲面，计算得到合理的网格尺寸函数。图11 显示了最终生成的数控机床横梁铸件的有限元网格，包含334，948 个顶点和1，279，473 个单元。在有限元计算中，上百万单元的网格已经需要较大规模的计算量了。

图10 渲染了网格尺寸函数的数控机床横梁铸件的隐式曲面

图11 为数控机床横梁铸件铸造工艺的有限元网格，可见此有限元网格的几何形状与原几何模型装配体基本一致。图12 显示了有限元网格的最终单元质量分布。从此图中可以看到，对于机床横梁铸件这类大型薄壁复杂铸件，本文提出的有限元网格生成算法仍然能保证最终的网格质量，质量大于0.8 的单元数大约占总单元数的60%，质量低于0.1的单元数为47 个。网格的整体质量满足有限元计算的要求。

图12 数控机床横梁铸件铸造工艺有限元网格的最终单元质量分布

3 结 论

本文提出了一种适用于任意复杂铸造工艺的有限元网格生成方法，其中包含以下几个关键技术和方法：a）隐式曲面几何描述方法；b）有限元网格尺寸计算方法；c）有限元网格生成和网格质量优化方法。经过两个实际生产的复杂铸造工艺STL 几何模型的测试，可以看到本文提出的有限元四面体网格划分算法能自动并顺利地划分出高质量的四面体有限元网格，实现了有限元网格划分的自动化和智能化。算法的稳定性具有工业强度，能满足实际工程应用的需求，为铸造CAE 技术的进一步推广和应用提供重要的技术保障。

[1]赵建华，陈红兵. 浅析铸造过程模拟仿真技术[J］. 铸造设备研究，2007（2）： 48-52.

[2]Gustafsson E，Hofwing M，Stromberg N. Residual stresses in a stress lattice-Experiments and finite element simulations[J］.Journal of Materials Processing Technology. 2009，209（9）：4320-4328.

[3]Ma D，Lin F，Chua C K. Rapid prototyping applications in medicine. Part 2： STL file generation and case studies[J］. The International Journal of Advanced Manufacturing Technology.2001，18（2）： 118-127.

[4]Qian J，Zhang Y. Sharp feature preservation in octree-based hexahedral mesh generation for CAD assembly models[J］. Proceedings of the 19th International Meshing Roundtable. 2010：243-262.

[5]Nunes C，Mesquita R C，Magalh A Es A. Implementation of boolean and assembly operations in a solid modeler[C］. 2010.

[6]Tautges T J. The generation of hexahedral meshes for assembly geometry： survey and progress[J］. International Journal for Numerical Methods in Engineering，2001，50（12）： 2617-2642.

[7]Sethian J A. Level Set Methods and Fast Marching Methods[M］.University of California，Berkeley，1999.

[8]Osher S，Fedkiw R. Level Set Methods and Dynamic Implicit Surfaces[M］. Springer，2003.