测试对导弹发射可靠性预测的影响分析*

锁斌，胡斌

(中国工程物理研究院 电子工程研究所，四川 绵阳 621900)

0 引言

导弹武器系统在经过长期贮存后，发射前通常需要通过对关键单元的测试对系统的当前状态和能否发射进行确认。然而，由于一些技术的原因，往往有部分关键单元难以测试，甚至不可测试。例如，一些涉及到安全性的组件、一次性使用组件等不能测试，需要特殊测试手段的组件在导弹贮存和发射前无法进行测试。这些不可测单元失效与否对导弹系统发射可靠性有着直接的影响，某些单元失效甚至会导致整个系统的失效。那么，仅仅测试其他可测单元对预测整个系统发射可靠性有无帮助？这些可测单元中，哪些单元的测试是最必要、最关键的？定量地回答这2个问题，对于测试方案的设计和优化有着重要的意义。

1 测试对单元发射可靠性预测的影响

对于某一单元，假设其可靠度函数为R(t)，测试时刻为t0，发射时刻为t0+Δt，则：

(1) 不对单元进行测试时，其发射可靠度为

RNT=P(T>t0+Δt)=R(t0+Δt)，

(1)

即该单元完成发射任务的可靠性预测值为RNT。

(2) 对单元进行测试时，若测试结果为单元失效，则显然单元不能完成发射任务，单元的发射可靠度预测值由RNT下降为0，相应的修正量为(R=-RNT；若测试结果为单元正常工作，则根据条件概率[1]，单元的发射可靠度为

RT=P(T>t0+Δt|T>t0)=R(t0+Δt)/R(t0).

(2)

对比式(1)，(2)显然有

RT>RNT.

(3)

也就是说，若测试结果为正常，则单元的发射可靠度预测值由RNT提高为RT，相应的修正量为

(4)

式(4)表明，修正量与单元在t0时刻的可靠度R(t0)密切相关，R(t0)越小，修正量越大，测试的必要性越大。该结论与直观经验非常吻合，说明对于可靠性很高的单元测试的必要性较小，而对于可靠性不高的单元则应作为测试的关注对象。

可见，单元在t0时刻的健康状态(正常或失效)直接影响其发射可靠度。如果不进行测试，简单地认为单元发射可靠度为RNT，将可能带来较大的预测误差。因此，为了准确预测发射可靠度，很有必要对单元进行测试，单元可靠度越低测试的必要性越大。

算例1：某单元的寿命服从指数分布，失效率为λ= 10-4/h，t0=2 000 h，Δt=50 h，则不测试时单元的发射可靠度为

RNT=e-λ(t0+Δt)=0.814 6.

测试时若单元能正常工作，则单元的发射可靠度修正为

RT=e-λΔt=0.995 0,

相应的修正量ΔR=0.180 4。

2 测试对系统发射可靠性预测的影响

一个系统通常是由若干个单元通过串联或并联的方式以某种拓扑结构组合而成的[2-4]。对于一些特殊的系统，如k/n系统[5-7]、桥式系统[8-9]等，可以通过一定的方式转换为串并联系统[10]。因此，在这里主要讨论测试对串并联系统可靠性评估结果的影响。下面以单元寿命服从指数分布为例，分别就串联系统、并联系统和串并混联系统展开讨论。对于单元服从其他分布的情况，分析的过程也是类似的。

2.1 串联系统

如图1所示，若系统由n个服从指数分布的相互独立单元串联组成，失效率分别为λ1,λ2,…,λn，则发射前不测试时系统的发射可靠度为

(5)

图1 串联系统Fig.1 Series system

假设前k个单元可测，后n-k个单元不可测。显然，若被测的k个单元中有任一单元失效，则整个系统失效。否则，由式(2)，第i(1≤i≤k)个单元的发射可靠度为

Ri(t0+Δt)/Ri(t0)=e-λiΔt,

(6)

此时系统的发射可靠度为

e-(λ1+λ2+…+λk)Δte-(λk+1+λk+2+…+λn)(t0+Δt).

(7)

算例2：某系统由3个服从指数分布的相互独立的单元串联组成，失效率分别为λ1= 2×10-5/h，λ2=3×10-5/h，λ3=5×10-5/h。t0=2 000 h，Δt=50 h。则不测试时系统的发射可靠度为

若单元2不可测，单元1和单元3经测试工作正常，则系统的发射可靠度为

相应的修正量ΔR=0.122 5。

2.2 并联系统

如图2所示，若系统由n个服从指数分布的相互独立单元并联组成，失效率分别为λ1,λ2,…,λn，则发射前不测试时系统的发射可靠度为

(8)

图2 并联系统Fig.2 Parallel system

假设前k个单元可测，后n-k个单元不可测。若经测试，k个单元中有m个单元正常，k-m个单元失效，则系统的发射可靠度为

(9)

算例3：某系统由3个服从指数分布的相互独立的单元并联组成，失效率分别为λ1= 2×10-4/h，λ2=3×10-4/h，λ3=5×10-4/h。t0=2 000 h，Δt=50 h。则不测试时系统的发射可靠度为

0.900 9.

相应的修正量ΔR=-0.360 3。

若单元1，3测试结果均为正常，则系统的的发射可靠度为

0.999 9，

相应的修正量ΔR=0.099。

若单元1测试结果为正常，单元3测试结果为失效，则系统的发射可靠度为

相应的修正量ΔR=0.094 1。

2#立喷：若在2#立喷浸水淬火，也会存在和1#立喷同样的问题，而2#立喷的优点是有各种配套附具，管板下部可以通过内环喷嘴提高冷却能力，但是，2#立喷配套的各种外环、内芯和垫铁都是根据其他专用产品尺寸量身定制，加氢管板尺寸能否和淬火设备配套的附具相适应也是存在的问题之一，这需要我们通过选取适合的附具、冷试、试吊来验证方案的可行性。另外，2#立喷尺寸本身就小且受外环管的影响，管板能否正常落入水槽也是当时存在的主要问题。

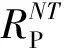
2.3 串并混联系统

串并混联系统通常可以逐级地转化为并联或串联系统。例如图3所示的串并混联系统，单元1，2和单元3，4分别构成2个并联子系统I和II，而子系统I和II又构成了一个串联系统。因此串并混联系统的分析方法与前面介绍的方法是类似的，在此不再赘述。

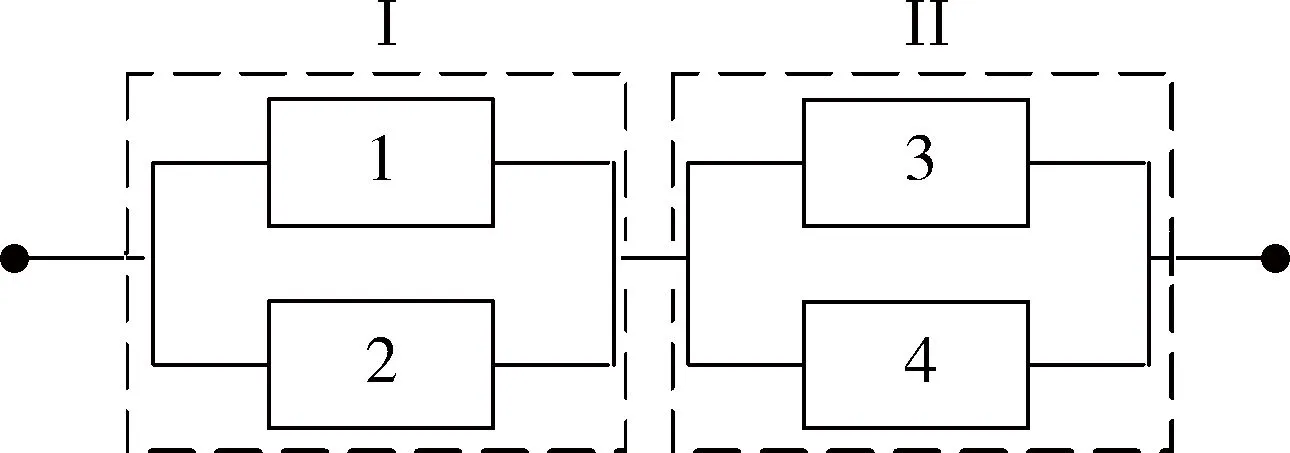
图3 串并混联系统Fig.3 Series and parallel system

3 测试重要度分析

导弹系统通常由若干个单元构成，上述分析结果表明，不同单元的测试与否对系统发射可靠性预测结果的修正程度是不同的。虽然在可靠性的故障树分析理论中已建立了概率重要度、结构重要度、关键重要度等3种重要度指标[11-12]，它们是从不同的侧面反映底事件的发生与否导致顶事件发生的影响程度，但这些指标并不能反映底事件单元的测试性对顶事件发生概率预测结果的修正程度。因此本文提出“测试重要度”这一指标，来度量各个单元的测试性对系统发射可靠性预测结果的修正程度。

测试重要度定义为：第i个单元在测试和不测试2种状态下系统可靠度修正值的绝对值，由于单元i测试后存在正常和失效2种状态，因此分2种情况计算系统发射可靠度修正值的绝对值并取加权平均，即

P(T>t0+Δt|Ti≤t0)-P(T>t0+Δt)w2，

(10)

式中：权重系数w1=P(Ti>t0)表示单元i在t0时刻正常工作的概率；权重系数w2=1-P(Ti>t0)表示单元i在t0时刻的失效概率。

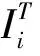
算例4：某导弹发动机失效的故障树如图4所示。图中给出了发动机点火失效、壳体爆破和壳体烧穿3种失效模式。

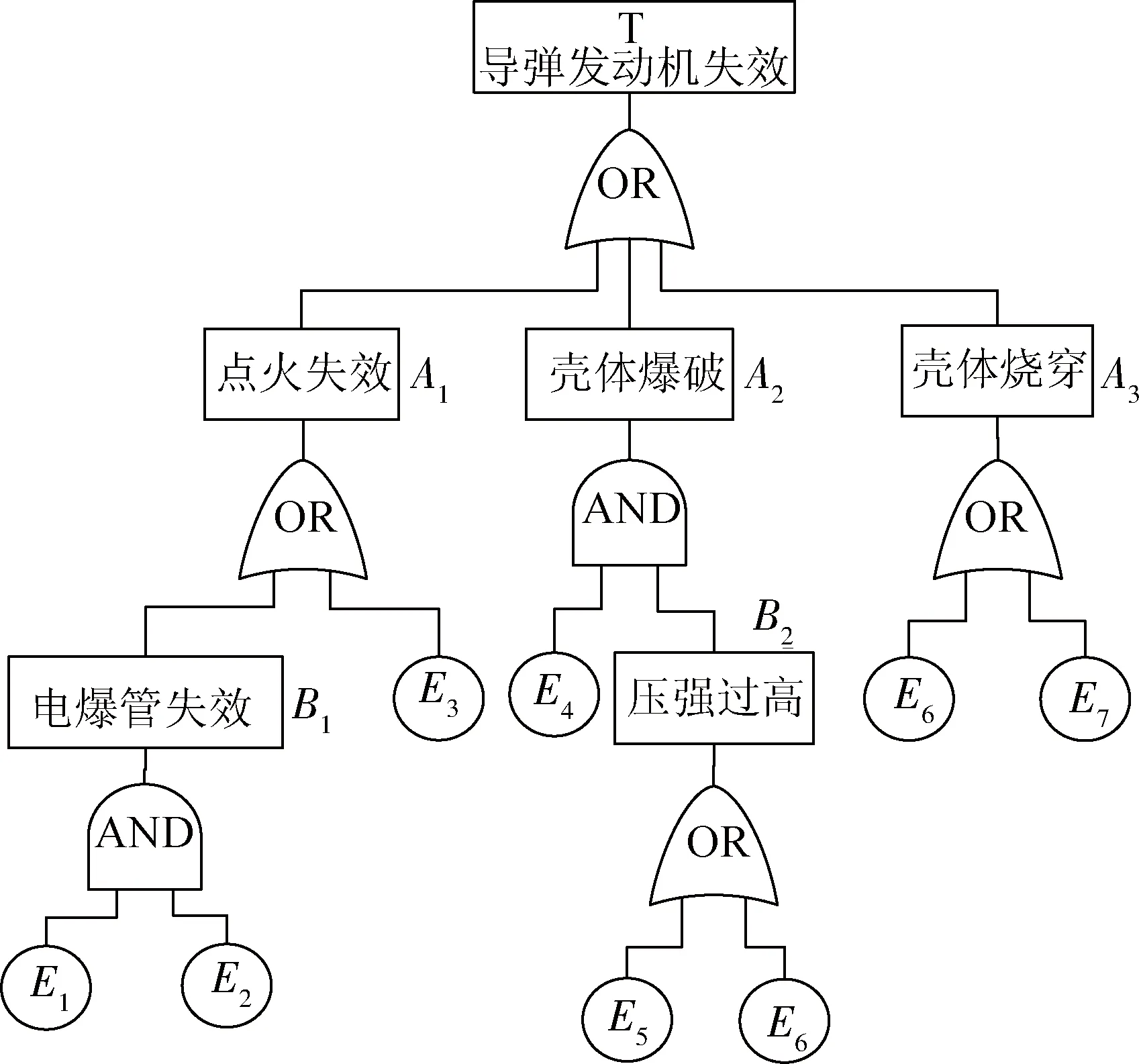
图4 导弹发动机失效的故障树Fig.4 Fault tree of missile motor

7个底事件中，E4和E6服从威布尔分布，其余服从指数分布，其分布参数如表1所示。

根据式(10)计算各个底事件的测试重要度，结果如表2所示。表中还给出了各个底事件的概率重要度、结构重要度和关键重要度。

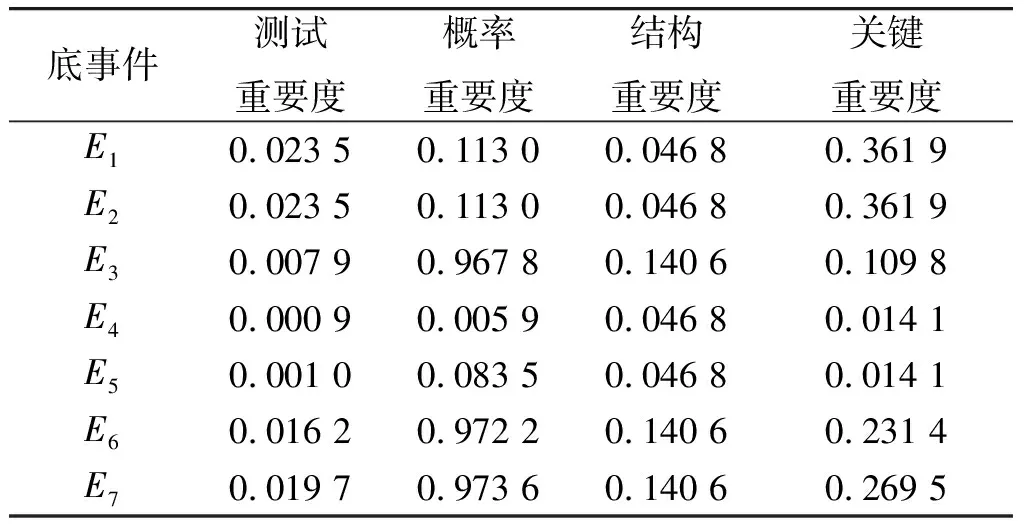
表2 重要度分析Table 2 Importance analysis

从表2的计算结果可以看出，各个底事件的测试重要度的排序和传统的3种重要度的排序并不相同。例如，E1，E2的测试重要度最大，而E4最小；而概率重要度的排序里，却是E6，E7最大，E4最小。因此，传统的3种重要度并不能反映出底事件在测试性上的重要程度。从定性的分析来看，E1，E2的失效概率比其他底事件大得多，两者为并联关系，因此当测试后确认其中任一个为正常时，系统的发射可靠度都会有较大幅度提高，从而使得测试重要度的值较大。表2的计算结果和定性分析的结果相吻合，较好地反映了客观事实。

4 结束语

本文定量地分析了单元的测试性对导弹发射可靠性预测结果的影响程度，并提出了测试重要度这一重要指标。算例分析表明，无论单元测试结果为失效还是正常，经过测试后得到的系统发射可靠度预测值与不测试时的结果可能有很大的差异，因此测试可以提高系统发射可靠度预测的准确程度。另外，通过计算提出的测试重要度，可以找出对系统发射可靠度预测结果影响较大的若干单元，从而为导弹测试方案的设计和优化提供理论依据。

参考文献：

[1] 周昊, 赵修平, 吴文军. 基于Bayes 理论的发射装置测试性评估方法研究[J]. 弹箭与制导学报, 2010, 30(3):253-256.

ZHOU Hao, ZHAO Xiu-ping, WU Wen-jun. Study on the Method of Testability Assessment of Some Launcher Based on Bayes Theory [J]. Journal of Projectiles，Rockets.Missiles and Guidance, 2010, 30(3):253-256.

[2] 牛绿伟, 高晓光, 张坤, 等. 串并联结构分解目标毁伤评估[J]. 火力与指挥控制, 2011, 36(9):140-144.

NIU Lü-wei, GAO Xiao-guang, ZHANG Kun, et al. Damaging Evaluation for Complex Targets Based on Series-Parallel Structure Decomposing [J]. Fire Control & Command Control, 2011, 36(9):140-144.

[3] 程江, 唐应辉. 单向关闭三部件串-并联可修系统的可靠性[J]. 系统工程学报, 2010, 25(5):717-722.

CHENG Jiang, TANG Ying-hui. Reliability of Three Units-Series-Parallel Connection with One Direction Shut-Off Rule [J]. Journal of Systems Engineering, 2010, 25(5):717-722.

[4] 孙永国, 孙永全, 郭建英. 串并联系统可用性优化方法[J]. 电机与控制学报, 2007, 11(2):315-317.

SUN Yong-guo, SUN Yong-quan, GUO Jian-ying. Availability Optimization Design of Series-Parallel System [J]. Electric Machines and Control, 2007, 11(2):315-317.

[5] 金星, 洪延姬, 张明亮, 等. 不同单元构成的任意 k/ N系统可靠度近似评定方法[J]. 弹箭与制导学报, 2004, 24(3):74-76.

JIN Xing, HONG Yan-ji, ZHANG Ming-liang, et al. Approximate Reliability Evaluation Method of k-out-of-N System Consisted of Different Units [J]. Journal of Projectiles.Rockets.Missiles and Guidance, 2004, 24(3):74-76.

[6] 宋月, 刘三阳, 冯海林. 相邻k-out-of-n:F多状态可修系统的可靠性分析[J]. 系统工程与电子技术, 2006, 28(2):310-316.

SONG Yue, LIU San-yang, FENG Hai-lin. Reliability Analysis of Consecutive k-out-of-n:F Repairable Systems with Multi-State Component [J]. Systems Engineering and Electronics, 2006, 28(2):310-316.

[7] 冯懿, 左德承, 李金锋, 等. 多态k-out-of-n:G型系统可用性评测[J]. 清华大学学报：自然科学版, 2011, 51(S1):1515-1518.

FENG Yi, ZUO De-cheng, LI Jin-feng, et al. Availability Evaluation of Multi-State k-out-of-n:G Systems [J]. Journal of Tsinghua University：Science and Technology-Version, 2011, 51(S1):1515-1518.

[8] 陈德新. 桥式系统的模糊可靠性[J]. 系统工程理论与实践, 1997, 12(11): 109-112.

CHEN De-xin.Fuzzy Reliability of Bridge Circuit Systems [J]. Systems Engineering—Theory & Practice, 1997, 12(11): 109-112.

[9] 莫文辉. 桥式系统可靠度失效树分析法[J]. 武汉汽车工业大学学报, 1997, 19(1):21-23.

MO Wen-hui. Fault Tree Analysis Method of Bridge System Reliability [J]. Journal of Wuhan Autmotive Polytechnic University, 1997, 19(1):21-23.

[10] 锁斌, 程永生, 曾超，等. 非精确概率下基于证据理论的典型系统可靠性模型[J]. 系统仿真学报, 2013, 25(2):317-321.

SUO Bin, CHENG Yong-sheng, ZENG Chao, et al. Reliability Model of Typical Systems for Imprecise Probability Using Evidence Theory [J]. Journal of System Simulation, 2013, 25(2): 317-321.

[11] 马德仲, 周真, 于晓洋,等. 基于模糊概率的多状态贝叶斯网络可靠性分析[J]. 系统工程与电子技术, 2012, 34(12):2754-2759.

MA De-zhong, ZHOU Zhen, YU Xiao-yang, et al. Reliability Analysis of Multi-State Bayesian Networks Based on Fuzzy Probability [J]. Systems Engineering and Electronics, 2012, 34(12): 2754-2759.

[12] 锁斌, 曾超, 程永生, 等. 证据理论与贝叶斯网络相结合的可靠性分析方法[J]. 系统工程与电子技术, 2011, 33(10):2343-2347.

SUO Bin, ZENG Chao, CHENG Yong-sheng, et al. Reliability Analysis Based on Evidence Theory and Bayesian Networks Method [J]. Systems Engineering and Electronics, 2011, 33(10):2343-2347.