小子样情况下的概率性能指标评定方法研究*

贾旭山，金振中

(1. 中国人民解放军92941部队，辽宁 葫芦岛 125001；2. 中国人民解放军92493部队,辽宁 葫芦岛 125001)

0 引言

针对小子样情况下的概率性能指标的评定，近年来开展了大量的研究工作并提出了一些方法，其中影响比较大的方法有二项分布Bayes假设检验方法[1-2](为简便计，下文简称P方法)，并在国家行业标准中推荐使用。然而，该方法在使用中逐渐暴露出一些问题需要分析并解决。

1 P方法简述

设概率性能指标记p，运用P方法的基本步骤如下：

(1) 给出原假设H0:p=p0;

(2) 选取鉴别比d，并根据如下公式确定备择假设H1:p=p1，其中:

(1)

(3) 根据历史信息确定验前概率。设历史试验信息成功数记S0、失败数记F0，则有验前概率

(2)

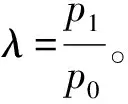
(4) 设试验数记N，确定检验临界值

(3)

(5) 设试验成功数记SN，则有如下检验方案

(4)

(6) 令απ0为生产方风险，βπ1为使用方风险，则有如下计算公式，运用中要求“双方风险相当并小于某一值”。

(5)

式中：α和β为经典方法时的双方风险,

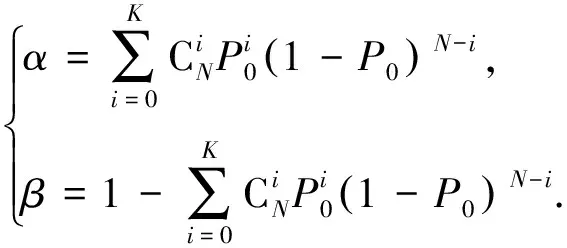
(6)

2 P方法问题描述

2.1 一致性问题

首先，P方法表述有矛盾。P方法自名为二项分布假设检验方法，但却引用了风险概念并给出了风险计算公式。实际上，假设检验属统计推断范畴，而风险概念却属决策范畴[3-4]，两者并不等同。

其次，P方法确定方案的做法矛盾。P方法通过似然比检验公式反推拒受临界值，运用时却又要求该方案双方风险相当，而实际上两者之间不一致，例如：令p0=0.8，p1=0.6，设π0=π1=0.5和N=7，则有K=4，απ0=0.074和βπ1=0.210，双方风险相差3倍。由于P方法没有限定鉴别比d的取值，有一些做法就试图通过调整d来满足风险相当要求[4]，这又造成了P方法的严谨性问题。

2.2 严谨性问题

对于概率性能指标的评定，如果指标值、验前信息和试验子样数量均确定，则评定标准应该唯一。P方法缺乏严谨性体现在d取值随意而致评定标准多样，例如以同等无知原则确定验前信息[5-6]并令p0=0.7，N=9，则d取不同值时出现不同的评定标准(检验临界值K)[7]，具体情况见表 1。

表1 评定标准与鉴别比Table 1 Evaluation criteria and the discernible ratio

2.3 正确性问题

P方法的应用要点是双方风险相当且都小(暂且忽略一致性问题)，因此其风险值是关键。P方法将经典方法视为无验前信息特例，因而当无验前信息时风险值应与经典方法应一致。观察P方法，显然当π0=π1=0.5，απ0=α/2和βπ1=β/2(α和β分别为经典方法的双方风险)。

2.4 有效性问题

首先，P方法将验前信息局限于历史试验信息，失去了Bayes方法的本义，因为在历史试验信息融合方面，经典方法与Bayes方法一致(证明略)。其次，P方法事实上无法对验前信息实现融合，文献[1]指出 “该方法(P方法)有其不足，当π0与π1相差较大时，双方风险难以相当，相应的检验方案较偏激，难以被双方共同接受”。举例说明如下：设有验前信息9发8中，现场试验数量5，则有π0=0.833 2，π1=0.166 8，απ0=0.170 6，βπ1=0.057 6，显然验前信息不可用。

3 P方法问题剖析

概括讲，P方法有3个深层次问题：①简单备择对抗简单假设的提法有错；②引入鉴别比d的做法简单、机械；③引入决策领域的风险术语是草率的。

3.1 关于简单备择对抗简单假设

P方法是用于概率性能指标评定的方法，概率的定义域是(0,1)，而P方法关于概率性能指标的提法却是两点分布-简单备择对抗简单假设，这既有悖对概率的常识性认识，也是问题的根本原因。Bayes方法设定在没有任何信息可用时可能的取值是同等无知，即各取0.5(纯随机)，而随着信息量加大随机性会减弱，即其中一个的概率会增大，而另一个会减小。实际上，理论上2类错误概率互补(即和为1)，不可能达到同等小；工程上由于容许误差(引入鉴别比)存在，其工程计算值可以同等小，但简单备择对抗简单假设的提法则消除了Bayes方法在工程上的这种可能性。

3.2 关于鉴别比

P方法没有考察鉴别比的数学或工程背景，而导致其取值随意[8]。实际上，鉴别比类似于经典统计学引入的一个符号，其目的是控制犯第Ⅱ类错误概率的“表现值”，其作用是确定计算第Ⅱ类错误概率“表现值”需用到的备择假设的“参考值”，所谓“表现值”和“参考值”，指不是真正的第Ⅱ类错误概率值和备择假设值，而仅指在工程范围内允许的近似值。之所以这样做，是因为一方面，理论上由于原假设与备择假设之间的连续性，使得无论样本容量多大2类错误概率和总为1；另一方面，工程上在误差允许范围内，为了同时控制2类错误概率，需要将原假设和备择假设分离，在经典统计学中的做法是保持原假设μ0而修改备择假设μ1，使μ1等于μ0+δ或μ0-δ[9]，这里的δ与P方法中的鉴别比d意义相同，区别在于前者用加(或减)，后者用乘(或除)。因此鉴别比的提出与确定应谨慎，P方法中关于鉴别比值的确定是草率的，具体情况见表 2。

表2 鉴别比对原假设、备择假设分离值影响Table 2 Influence on the separated level between null hypothesis and alternative hypothesis by the discernible ratio

3.3 关于决策风险

P方法其实属基于后验概率的似然比检验方法，P方法所有的步骤和概念均可以在统计推断的假设检验领域解释清楚，然而P方法却引入决策风险的概念[7]，由此又引出如下问题。

(1) 关于决策问题3要素：状态集、行动集和损失函数。P方法均不涉及，只是套用了一个背景意义和表现值均与错误概率相同的风险概念，彰显P方法的不严谨性。

(2) Bayes决策范畴包含4类风险概念：先验风险、决策风险、后验风险和Bayes风险，其中先验风险和后验风险是样本空间的函数，Bayes风险是数值，决策风险是状态集的函数。如果将假设检验问题视作基于0-1损失函数的决策问题，则经典假设检验方法中的风险α，β与Bayes决策中的决策风险相对应，Bayes风险则为π0β+π1β，由此P方法中的风险在Bayes决策中找不出对应的概念。如果认为Bayes决策关于风险概念是完备的，则P方法中的风险公式是错误的。

(3) 如果将P方法视作基于后验概率的似然比检验方法，其风险公式就是错误概率公式[10]，然而这个公式有误，因为它不是基于后验概率计算的，因为在简单备择对抗简单假设的情况下，后验概率公式并不容易导出。P方法只是在经典方法的基础上，将2类风险与验前概率对应相乘，这样做的背景、意义和逻辑性确实不清楚。

4 小子样评定方法改进研究

4.1 小子样问题及形式化描述

随机现象需要通过大量重复试验揭示其规律性，如果试验的数量(即子样量)有限就不能有效揭示其规律，这是小子样问题的实质[11]。如果将小子样问题简单、模糊地描述为“子样数比较少”，则无法界定和解决小子样问题，比如：“10个是否小子样”。根据统计学大数定理，样本容量与随机不确定度负相关，假设检验不确定度可用2类错误概率来表示，因此小子样问题形式化描述步骤如下：

(1) 根据数学或工程背景将原假设域与备择假设域相分离，对于概率性能指标以通常的0.05显著性水平定分离值，在作显著性检验时将备择假设域作退让以分离，在作似然比检验时将原假设域和备择假设域作同等退让以分离；

(2) 以通常的0.05显著性水平定2类错误概率值的允许水平(上限)；

(3) 将样本容量从1开始逐步增大，计算2类错误概率，当2类错误概率同时小于允许水平时的样本容量是最小需求量；

(4) 当可用样本量小于最小需求量时，随机试验存在小子样问题，否则不存在小子样问题。

4.2 小子样评定方法改进的基本思路

小子样评定方法改进的基本思路是要解决P方法存在的问题，具体要求为：采用复杂备择对抗复杂假设；取消鉴别比，而改由工程或数学背景[12]来确定原假设与备择假设的分离水平；取消决策风险，同时控制2类错误概率与风险相当原则的意义一致；以贝塔分布作为概率性能的分布族，理由有3点：①因为两者的定义域相同；②因为贝塔分布为单峰分布，且峰度随参数(对应样本量)增大而减小，符合大数定理；③因为贝塔分布与二项分布为共轭分布。

4.3 小子样评定方法改进——L方法

改进后的小子样评定方法命名为L方法，具体步骤如下：

(1) 描述概率性能指标值，如要求命中概率大于等于p′。

(2) 以0.05的显著性水平同等退让后提出原假设和备择假设：

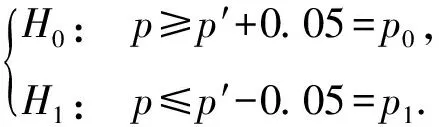
(7)

(3) 以同等无知原则确定概率性能的初始验前分布beta1,1，该分布表示在没有任何信息时概率性能在区间0,1上等可能取值。

(4) 以0.05的显著性水平确定2类错误的允许水平。

(5) 确定样本最小需求量。为简单计采用探索法确定，样本容量设为n、初值取1、逐步增1，拒受临界值设为k、初值取0、逐步增1至n，以式(8)计算2类错误概率α，β，直至两者均小于允许水平，这时n的取值就是样本最小需求量n′。

(8)

式中：B表示贝塔分布的概率累积函数。

(6) 判定是否小子样问题。设随机试验可用样本量n，则有如下判别式：

(9)

(7) 搜寻验前信息，得到验前分布。对于概率性能指标，验前分布族为贝塔分布，对于历史试验信息可直接确定，验前分布的表现形式为betak0+1,n0-k0+1，若有n0+n≥n′则可采用小子样方法进行评定，否则还需继续搜寻验前信息。

(8) 进行Bayes评定，有后验分布beta(k+k0+1,n+n0-(k+k0+1))。

(10)

(9) 重新计算2类错误概率，公式如下：

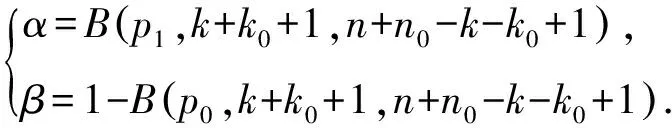
(11)

4.4 L方法示例

令p′=0.7，并以0.05的显著性水平同等退让后提出原假设和备择假设，以同等无知原则设定p的初始验前分布beta1,1，确定2类错误的允许水平为0.05，则可确定样本最小需求量n′=229。设随机试验可用样本量n=9，则可判定试验面临小子样问题。若有验前分布beta182,49，并设现场试验信息为9发8中，则有后验分布beta190,50，根据下式似然比计算结果判定接受原假设，并有α=0.048 4和0.041 6。

(12)

关于L方法有几点补充说明：

(1) 可以看出，L方法对样本需求量比较大。当从统计角度以显著性水平0.05严格限定原假设和备择假设退让水平、及2类错误概率的允许水平时，实际情况是这样的；当做法类似P方法，以0.1作为同等退让水平、以0.3作为2类错误概率的允许水平时，样本需求量为8，2类错误概率为α=0.231 8和β=0.261 8，其效果与P方法相当。该现象反映出L方法相比P方法并不偏激，它只是对方法应用时的样本量条件提出了严格要求，这也应作为小子样方法的基本应用前提，否则小子样方法就成了小子样情况下的大子样方法。

(2) 当P方法的原假设和备择假设分别对应L方法原假设和备择假设的边界值，且样本量相等时，2方法的方案一致，错误概率相当但有差异。该现象反映出L方法与P方法效果相当。错误概率的计算差异反映出2类方法的基本思想不同，P方法是固定概率值对抽样值作累积，L方法则是固定抽样值对概率作累积，因此两者计算值相当却有差异，2种方法的对应计算结果见表 3。

表3 L方法与P方法效果比较Table 3 Comparison of effect of method L and method P

(3) L方法解决了验前信息融合问题，举例如下：设p0=0.75，p1=0.65，有验前信息9发8中，现场试验量为5，则2个方法对比见表4。从中看出P方法2类风险差值达到0.12、比值超出3倍，L方法则基本属同一数量级；P方法风险好像有明显减小，但由于存在计算错误的问题，因此不具有表征意义，而L方法在融合了验前信息之后双方风险确实有明显减小。

表4 L方法有效性案例Table 4 Case of effectiveness of method L

5 结束语

小子样方法解决小子样问题的关键在于验前信息的融合，在无验前信息可用时小子样方法的效果应与经典方法应一致，小子样方法也应注重工程背景，而且不应使方法无意义地复杂化。本文对二项分布Bayes假设检验方法的有关这类问题进行了深入剖析，提出了具体改进改施，并通过对比验证了改进的有效性，但须指出解决小子样问题的关键在于针对具体应用背景的验前信息的获取。

参考文献：

[1] 曲宝忠,孙晓峰,李守秀,等.海军战术导弹试验与鉴定[M].北京:国防工业出版社,2005.

QU Bao-zhong, SUN Xiao-feng, LI Shou-xiu, et al.Naval Tactical Missile Test and Evaluation[M].Beijing:National Defense Industry Press,2005.

[2] 杨榜林,岳全发,金振中,等.军事装备试验学[M].北京:国防工业出版社,2002.

YANG Bang-lin, YUE Quan-fa, JIN Zhen-zhong, et al.Armament Test Theory[M].Beijing:National Defense Industry Press,2002.

[3] 贾乃光.统计决策理论与贝叶斯分析[M].北京:中国统计出版社,1991.

JIA Nai-guang.Statistical Decision Theory and Bayesian Analysis[M].Beijing:China Statistics Press,1991.

[4] 张尧庭,陈汉锋.贝叶斯统计推断[M].北京:科学出版社,1991.

ZHANG Yao-ting, CHEN Han-feng.Bayesian Statistical Infer[M].Beijing:Science Press,1991.

[5] 茆诗松.贝叶斯统计[M].北京:中国统计出版社,1999.

MAO Shi-song.Bayesian Statistics[M].Beijing:China Statistics Press,1999.

[6] 唐雪梅,张金槐,邵凤昌,等.武器装备小子样试验分析与评估[M].北京:国防工业出版社,2001.

TANG Xue-mei, Zhang Jin-huai, Sao Fen-chang, et al.Test Analysis and Evaluation of Weapon Systems in Small-Sample Circumstances[M].Beijing:National Defense Industry Press,2001.

[7] 贾旭山,金振中.二项分布贝叶斯假设检验方法[J].现代防御技术,2008,36(5):37-40.

JIA Xu-shan, JIN Zhen-zhong. Bayes Hypothesis Testing for Binomial Distribution[J].Modern Defence Technology,2008,36(5):37-40.

[8] 贾旭山,金振中.二项分布假设检验样本容量分析[J].现代防御技术,2012,40(4):67-70.

JIA Xu-shan, JIN Zhen-zhong. Bayes Hypothesis Testing and Sample Quantity[J].Modern Defence Technology,2012,40(4):67-70.

[9] 盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2001.

SHENG zhou, XIE Shi-qian, PANG Cheng-yi. Probability Theory and Mathematical Statistics [M].Beijing:Higher Education Press,2001.

[10] 贾旭山,金振中.武器系统概率指标评定[J].现代防御技术,2011,39(2):50-53.

JIA Xu-shan, JIN Zhen-zhong. Bayesian Decision Evaluation on Probability Indes of Weapon System[J].Modern Defence Technology,2011,39(2):50-53.

[11] 王国玉,申绪涧,汪连栋,等.电子系统小子样试验理论方法[M].北京:国防工业出版社,2003.

WANG Guo-yu, SHENG Xu-jian, WANG Lian-dong,et al.Test Theory and Method of electronic System in Small-Sample Circumstances[M].Beijing:National Defense Industry Press,2003.

[12] Thomas Leonard,John S J Hsu.Bayesian Methods:An Analysis for Statisticians and Interdisciplinary Reserachers[M].Beijing:Machinery Industry Press,2006.