基于预测控制的导弹俯仰通道制导控制一体化设计
水尊师,魏东辉,徐 骋
(北京机电工程研究所,北京 100074)
0 引言
制导控制一体化设计思想与传统的制导、控制独立设计不同,它将弹目相对运动关系和导弹自身的动力学特性作为一个整体的被控对象来研究,因此能够充分利用制导和控制回路之间的耦合关系,实现制导与控制回路间的最优化协调,从而利于导弹机动性能的发挥以及命中精度的提高。
国内外学者对导弹制导控制一体化进行研究,取得了一些成果。Lin[1]通过将传统的制导设计和控制集成,采用最优方法最先开展了导弹的制导控制一体化研究。文献 [2]采用终端滑模设计了一体化控制律。文献 [3]利用特征结构配置方法设计了俯仰通道控制律。文献 [4]和 [5]利用线性最优控制对导弹进行制导控制一体化设计,采用次优化θ-D控制方法完成了导弹的制导与控制一体化的设计。目前,制导控制一体化设计方案较多,包括六自由度模型 θ- D[5],反馈线性化控制[6],SDRE 控制[7],动态逆方法[8],这些设计更多的集中在采用一个框架将制导方程和控制方程统一起来,但是对于制导回路和控制回路之间固有的时间尺度仍然没有深入研究,难以实现制导与控制回路间的高度优化协调,不利于充分发挥导弹的机动性能和进一步提高导弹的命中精度。
本文首先介绍了制导控制一体化产生的优势,其次分析了时间尺度差异对制导控制一体化设计的影响,接着提出采用预测控制来体现时间尺度的差异性影响,通过对未来一段时间状态变量变化过程的预测来准确捕获动态过程特征,利用连续时间非线性预测控制,实现在线控制律的生成。
1 时间尺度影响分析
在导弹等飞行器运动中,存在固有的时间尺度,一般分为短周期的姿态运动过程和长周期的质心运动过程。这主要由于控制导弹运动的舵面一般较小,舵面偏转时,仅能产生较小的力,但由于力臂一般很大,能够产生较大的控制力矩。导弹在转动力矩的作用下通过姿态变化产生气动角 (攻角、侧滑角),进而控制导弹质心的运动。而在制导控制一体化设计过程中,如果导弹直接采用舵面产生的力来控制质心运动,这不符合物理本质,对于尾舵控制的导弹,如果舵面直接控制质心运动可能导致姿态控制发散。
目前已经有文献注意到由于时间尺度造成的影响,文献[5]在弹体坐标系建立了六自由度一体化方程,通过零化视线角速率和姿态角速度,采用θ-D方法获得控制律,研究结果表明所推导最优控制律对于权系数极度敏感,分析原因是由于舵偏同时控制质心运动和姿态运动时,导致对舵偏角互相矛盾的需求,提出基于速度坐标系的控制方法处理该问题。文献 [9]也表明时间尺度问题造成权系数很难选择,除非导弹和目标已经处于碰撞三角形,文献 [9]采用MPSP根据位置信息直接生成弹体角速度作为制导指令,再采用动态逆进行跟踪的控制方法,但其本质上制导和控制仍然是分开设计的。
为了能够体现时间尺度,需要对导弹的状态进行预测,该时间过程应能体现舵偏引起的气动角 (攻角、侧滑角)变化产生气动力的过程。本文采用预测控制来设计一体化控制律[10]。
2 导弹俯仰通道制导控制一体化模型
本文只研究导弹的俯仰通道,暂不考虑通道间的耦合,图1为弹目相对运动的几何关系示意图,可以得到如下的导弹的俯仰通道数学模型。

其中r,q,θ分别是弹目之间的相对距离,视线角和弹道倾角。
对式 (2)微分可知

忽略末制导阶段速度的变化,令Vq=rq·,考
虑到

图1 弹目相对运动关系Fig.1 Two-dimensional dynamics between missile and target

可知:

导弹俯仰通道动力学方程为[3]:

导弹制导控制系统的任务不仅是获得最小的脱靶量,而且很多情况下还要求在命中时刻有一定的命中角度,使战斗部获得较好的杀伤效果。假设qd为导弹落地时刻期望的视线角,考虑下式
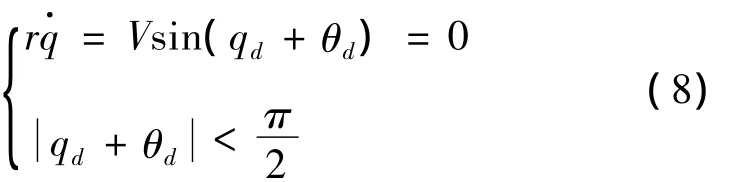
可知qd=-θd。
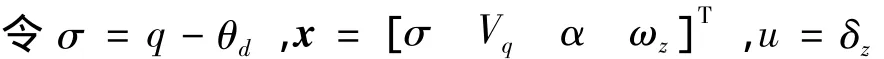
则可以获得如下的方程


3 基于预测控制的制导控制一体化设计
预测控制是一种非线性最优控制,在电力、炼油、化工和造纸等工业生产领域中有广泛的应用,其主要特征是在线滚动优化。最优控制往往采用状态向量和控制向量的组合作为二次型性能指标,其积分区间则是从初始时刻到最终时刻,而预测控制利用滚动的有限时段的优化取代了全局优化,能够顾及不确定性的影响,因此对于扰动、不确定性具有很好的鲁棒性。
为了保证导弹能够在末端以一定的角度击中目标并且稳定飞行姿态,希望状态变量[σ Vqωz]T→[0 0 0]T。本文采用泰勒展开的方法预测非线性系统的状态及输出响应,滚动优化由响应误差和控制能量组成的性能指标,使性能指标最小,得到一个非线性最优反馈控制律[10]。
考虑如下的非线性系统

如果当前的状态和控制已知,那么下一时刻系统的响应就可以通过积分预测得出。本文采用如下泰勒展开的方法来进行预测。
设λi为系统输出yi的相对阶,即为了明确出现控制u需要对yi求导的最小次数。定义
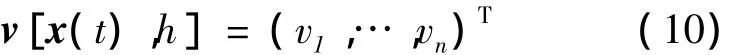

式中,ci为c(x)的第i个分量;h>0,为一个正实数,相当于预测步长;Lkf(ci)为 ci对 f的 k阶李导数。
在任何时刻t∈ [ 0 tf],将来的状态由现在的状态x(t)和控制u(t)决定,如果对每个小的步长h>0,将yi(t+h)在t处进行ri阶泰勒展开,可以得到

式中,Q∈ Rl×l为正定矩阵;R∈ Rm×m为半正定矩阵。
同样,将q(t+h)进行r阶泰勒展开得到

将y(t+h)和g(t+h)带入式,可知对于控制u(t),当∂J/∂u=0时,可以得到最优的预测控制器:

式中,e(t)=y(t)-g(t),为当前的跟踪误差,v(x,h)-d(t,h)为下一步的预测误差。
当系统的动态特性是线性离散时,h相当于采样时间,式 (16)推导出的控制律式就是一步超前最优预测控制律。按照上面的步骤,根据相对运动方程式 (1)可知λ1=2,λ2=1,λ3=1。假设

将式 (17)、式 (18)和式 (19)代人式 (16)即可得到制导控制一体化控制律,其中h相当于预测步长,选取中应充分考虑预测时间长短,同时h决定误差收敛的速度,h越小,误差收敛得越快,需要的控制量也越大[10]。
Q1,Q2,Q3分别表示视线角、视线角速度和俯仰角速度跟踪误差的权重,数值越大,对应的跟踪误差越小。
4 仿真结果与分析
本节采用某导弹参数进行导弹俯冲攻击段的制导控制一体化设计仿真。仿真条件设为:初始末制导距离为5657m,初始视线角为-45°,导弹的初始弹道倾角为0°,末端弹道倾角为-90°,最大舵偏角限制为25°。
选择预测步长h=0.1s,Q1=8000,Q2=20/(R+100),Q3=2,R=20。对于Q2的选择,主要考虑如果初始阶段Q2值较大,则弹道的视线角速度很快收敛到零,难以满足末端角度约束,因此考虑采用较小的初始值来形成一定的弹道形态,末端采用较大的值来保证末端的脱靶量。
导弹的脱靶量为1.5m,末端的弹道倾角为-89.08°,实现了垂直打击,仿真结果如图2~图5。
由图2,图3可以看出导弹以-89°弹道倾角击中目标。由于弹目接近碰撞时,视线角速率出现发散,因此控制量即俯仰舵偏角在末端出现一个较大的跳变,见图4。

图2 弹道图Fig.2 The trajectory of missile
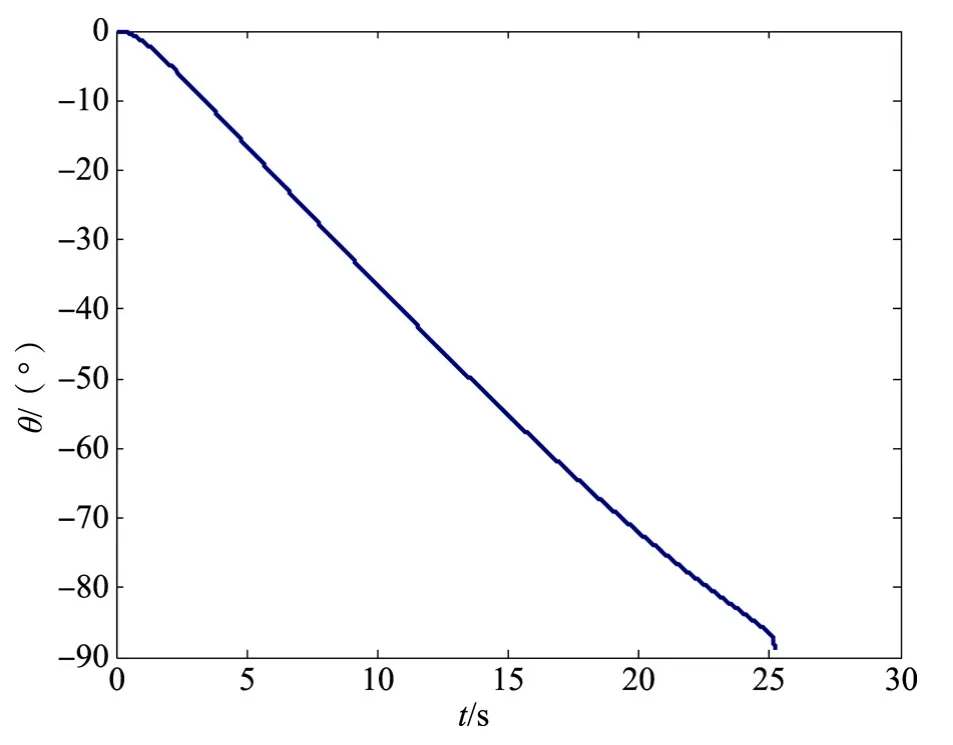
图3 弹道倾角图Fig.3 The curve of flight path angle
5 结论
本文针对制导控制一体化设计过程中固有的时间尺度差异特性,分析了时间尺度差异的影响,采用连续时间预测控制设计了一种一体化控制策略。通过对一段时间以后状态变量的预测,更好的反映实际的物理过程,导弹纵向平面非线性数值仿真表明,导弹满足终端角度约束的同时,脱靶量较小,姿态实现了稳定设计,所设计的制导控制一体化方案是合理有效的。后续将研究全空间状态下的制导控制一体化。

图4 舵偏角曲线Fig.1 The curve of pitch rudder

[1]Lin C F,Ohlmeyer E,Bibel J E,et al.Optimal design of integrated missile guidance and control[R].AIAA -98-5519,1998.
[2]查旭,崔平远,常伯浚.攻击固定目标的飞行器制导控制一体化设计 [J].宇航学报,2005,26(1):13~18.[ZHA Xu,CUI Ping-yuan,CHANG Bo-jun.An integrated approach to guidance and control for aircraft applying to attack the ground fixed targets[J].Journal of Astronautic,2005,26(1):13~18.]
[3]梁冰,徐殿国,段广仁.导弹俯仰通道带有落角约束的制导与控制一体化设计 [J].科学技术与工程,2008,8(1):70~75.[LIANG Bing,XU Dian-guo,DUAN Guangren.Integrated guidance and control with terminal angular constraint for the missile's pitch plane [J].Science Technology and Engineering.2008,8(1):70 ~75]
[4]Xin,M.and Balakrishnan,S.N.,Ohlmeyer,E.J.,Integrated guidance and control of missiles with Theta-D method,IEEE Transactions on Control System Technology,Nov,2006.
[5]Dancer M W,Balakrishnan S N,Ohlmeyer E J.Discussion and analysis of missile IGC design[C].AIAA Guidance,Navigation and Control Conference and Exhibit,Honolulu,Hawaii,2008.
[6]Menon,P.K.and Ohlmeyer,E.J.Nonlinear integrated guidance and control laws for homing missiles[C],AIAA Guidance,Navigation and Control Conference and Exhibit,Montreal,Canada,2001:1~9.
[7]Palumbo N.F.,Jackson T.D.,Integrated guidance and control:a state dependent ricatti differential equation approach[C],IEEE International Conference on control Applications,Piscataway,NJ,1999.
[8]Shu Yanjun,Tang Shuo.Integrated robust dynamic inversion design of missile guidance and control based on nonlinear disturbance observer[C].2012 4thInternational Conference on Intelligent Human-Machine systems and Cybernetics.2012:42~45.
[9]Padhi R,Chawla C,Das P G,et al.Partial integrated guidance and control of surface-to-air interceptors for high speed targets[C].2009 American Control Conference.Hyatt Regency Riverfront,St.Louis,MO,USA,2009:4184~4189.
[10]Lu P.Nonlinear predictive controllers for continuous systems[J].Journal of Guidance,Control and Dynamics,1994,17(3):553~560.
[11]水尊师,周军,葛致磊等.基于预测控制的角度约束制导律设计 [J].飞行力学,2011,29(3):56~59.[SHUI Zun-shi,ZHOU Jun,GE Zhi-1ei.Guidance with impact angle constraint based on predictive control[J].Flight Dynamics,2011,29(3):56 ~59.]

