高超声速飞行器强鲁棒自适应控制器设计新方法

任 章，廉成斌，熊子豪

（1．北京航空航天大学自动化科学与电气工程学院，北京，100191

2．飞行器控制一体化技术国防科技重点实验室，北京， 100191）

0 引言

高超声速飞行器的定义是指飞行速度大于5Ma的有翼或无翼飞行器［1］。高超声速飞行器整个飞行任务过程中飞行空域变化大，飞行速度变化范围宽，且大包线高动态飞行环境恶劣，内外部干扰严重，使得高超声速飞行器的系统参数大范围剧烈变化，且存在严重的不确定性。因此，面对高超声速飞行器这一类参数大范围剧烈变化，具有严重不确定性和内外部干扰的强耦合非线性被控对象，一般的鲁棒控制、自适应控制方法难以奏效，设计出的控制系统难以适应系统参数大范围剧烈变化以及严重不确定性，对内、外部干扰具有强抑制能力也较弱，不能满足高超声速飞行器的控制需求。

论文以助推滑翔式高超声速飞行器为被控对象，针对高超声速飞行器再入返回飞行过程中系统参数大范围剧烈变化以及存在严重不确定性的特点，同时考虑外界环境干扰复杂，内部干扰严重的特殊问题，提出了一种新型强鲁棒自适应控制器构型。新构型控制器分为主控制器+补偿控制器，且主控制器、补偿控制器可分开设计。主控制器面向标称系统，可采用成熟的控制理论来设计，比如设计PID控制器，使闭环系统具有工程要求的性能;将系统参数大范围剧烈变化、系统的不确定性以及内、外部干扰等视为“系统扰动”，采用合适的手段估计“系统扰动”并作为补偿控制器的输入，通过设计强鲁棒自适应补偿控制器对“系统扰动”进行补偿，在主控制信号和补偿控制信号的共同作用下，保证闭环系统稳定且满足工程要求的控制性能，从而使闭环系统对“系统扰动”具有强鲁棒性。这种强鲁棒自适应控制方法大大提高了高超声速飞行器控制系统对内、外部干扰的抑制能力和对系统参数大范围剧烈变化以及严重不确定性的适应能力。

1 新型强鲁棒自适应控制器

1.1 新型强鲁棒自适应控制器的原理

无论是古典控制理论还是现代控制理论，在被控对象具有精确数学模型的基础上，它们都是从一个系统的数学模型出发，设计一个控制器，使该系统满足特定的性能指标要求。然而，在实际问题中，因为工况变化、外部干扰、未建模误差以及系统的各种故障等缘故，对象的数学模型不可避免地存在着各种形式的不确定性，实际被控对象的精确模型很难得到。鲁棒自适应控制研究的主要问题是当系统存在不确定性和外在干扰时，如何设计控制律使闭环系统具有更强鲁棒性。本文首先以线性系统为对象，说明新型强鲁棒自适应控制器的构成原理。图1是传统的反馈控制系统原理结构图。

其中，被控对象P的标称模型为P0，K0为能稳定标称模型P0的一个标称控制器。当被控对象P具有较大的不确定性时，期望控制器能够“自适应”地变为鲁棒控制器K，使系统稳定并满足性能要求。研究表明［2］，通过适当改变控制器结构，确实存在一种可以同时兼顾系统性能和鲁棒性的鲁棒控制器结构。

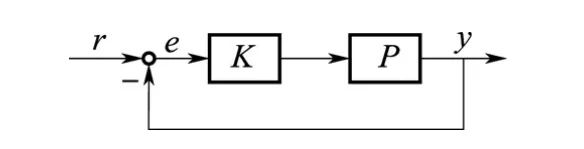
图1 传统反馈控制系统原理结构图Fig.1 The scheme of traditional feedback control system

通过适当的变换，可将控制器K实现成下图所示的形式。

图2 新型强鲁棒自适应控制器结构Fig.2 The scheme of novel strength robustness adaptive controller

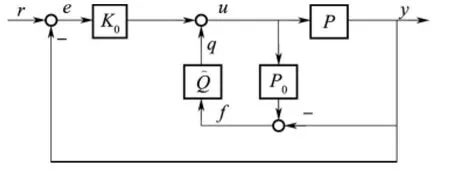
图3 P0和K0都稳定时，新型鲁棒控制器结构Fig.3 The scheme of novel strength robustness adaptive controller，when P0and K0stable

从以上结构可以看出，鲁棒控制器的内环由观

这种控制器构型的特别之处在于，当不考虑系统参数偏差和不确定性时，被控对象P=P0=，内回路中f可视为观测器误差，可视为补偿控制器。此时f=－=0 ，补偿控制器的输入为零，输出为零，补偿控制信号为零，对被控对象不起控制作用;当系统参数相对于标称系统发生变化或存在不确定性时，观测器误差f≠0，内回路控制器Q输出一个附加的补偿控制信号，用以补偿参数变化和不确定性的影响。故称这种控制器为新型强鲁棒自适应控制器。这种控制器构型由美国路易斯安那州立大学周克敏教授和北京航空航天大学任章教授首次提出，并给出相应的稳定性证明［3］。由于这种新型控制器结构可以克服传统的控制器设计中系统性能和鲁棒性难以同时兼顾的缺陷，具有较好的工程应用前景，近年得到了控制领域的广泛关注和多种形式的拓展推广。

1.2 面向非线性系统的新型强鲁棒自适应控制器构型拓展

将面向线性系统的新型强鲁棒控制器构型和设计思想推广到非线性系统，可得到面向非线性系统的新型强鲁棒自适应控制器构型如下图［4］:

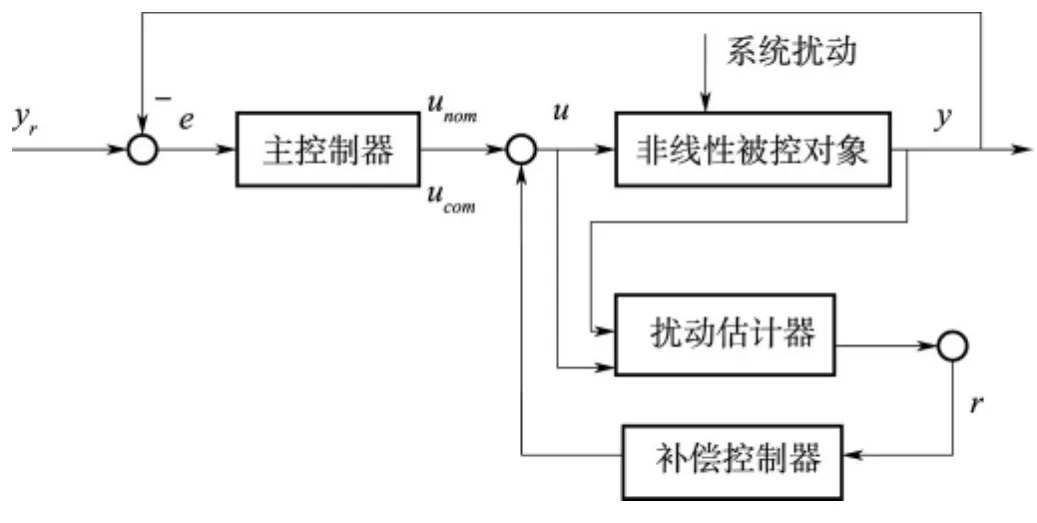
图4 新型强鲁棒自适应控制器构型Fig.4 The scheme of novel strength robustness adaptive controller

由图4可见，新型强鲁棒自适应控制器可分为两部分，一部分是以跟踪误差为输入的主控制器，另一部分是以扰动估计误差为输入的补偿控制器。这里的“系统扰动”指的是系统参数变化、系统不确定性或内、外部干扰等。主控制器面向被控对象的标称模型设计，主要考虑闭环系统的性能，可采用现有成熟的控制方法 （如PID控制）来设计;补偿控制器主要考虑当系统参数大范围变化、存在不确定性或有内、外部干扰时，在保证闭环系统稳定的前提下，合理设计补偿控制器，对参数大范围变化、不确定性或内、外部干扰进行有效补偿。以此保证受控系统在参数大范围变化、具有不确定性或存在内、外部干扰的情况下，在两个控制器的共同作用下，可保证闭环系统稳定，并使闭环系统满足工程要求的性能。

当无“系统扰动”时，仅主控制器起作用，补偿控制器无输出;当有“系统扰动”时，通过对“系统扰动”进行估计，并作为补偿控制器的输入信号，驱动补偿控制器输出合适的补偿信号来克服“系统扰动”的影响。补偿控制器的这种工作模式特别适合高超声速飞行器飞行控制系统的设计。由于可采用现有成熟的控制理论和方法（如PID控制）来设计控制器，故下面将重点研究“系统扰动”的估计和补偿控制器的设计。

2 “系统扰动”的估计和补偿控制器的设计

针对标称模型已知的放射非线性系统，可采用标称微分估计器和非线性扩张状态观测器（Nonlinear extended state observer，NESO）估计系统参数大范围剧烈变化、系统的不确定性以及内、外部干扰等造成的“系统扰动”。传统的方法利用非线性跟踪微分器获取了实际状态的微分，将其与标称微分估计模型输出比较得到的残差的方法简单直观，但是由于非线性跟踪微分器的能力有限，残差信号容易受到噪声信号影响，实际工程上应用并不理想。本文考虑利用非线性观测器技术估计“系统扰动”。

根据新型强鲁棒自适应控制器的构成原理，可用“观测器”来估计“系统扰动”。对于非线性系统来讲，可用于估计“系统扰动”的非线性观测器有非线性干扰观测器、滑模干扰观测器、神经网络干扰观测器和扩张状态观测器 （Extended state observer，ESO）［2］。非线性干扰观测器的输出为系统的干扰，且需要已知系统的所有状态;滑模干扰观测器可以同时估计系统的状态和干扰，但是由于引入输出误差的变结构校正，容易引入颤振现象;神经网络干扰观测器的输出为系统的干扰，但是训练复杂，且学习时间较长。因此，本文主要研究利用非线性扩张状态观测器NESO（Nonlinear extended state observer）来估计“系统扰动”，并基于NESO的输出来设计补偿控制器。

2.1 扩张状态观测器NESO的设计

扩张状态观测器是一种基于输出误差校正的状态观测器，它不仅可给出控制对象的状态量，还可以估计模型不确定性和扰动的实时值，实时值即为扩张状态，故称为扩张状态观测器［5－6］。

设带有系统扰动的n阶仿射非线性系统为:

式中，β1，β2，…βn为适当的参数，fci（e1），i=1，2，…，n，是满足条件:e1fci（e1）≥0的适当的非线性函数。

把作用于开环系统的加速度函数f（x1，x2，…，xn）和干扰扩张成新的状态变量xn+1，记为xn+1=f（x1，x2，…，xn）+w（t），并假设x·n+1=v（t），那么系统 （2）可以扩张成新的系统:

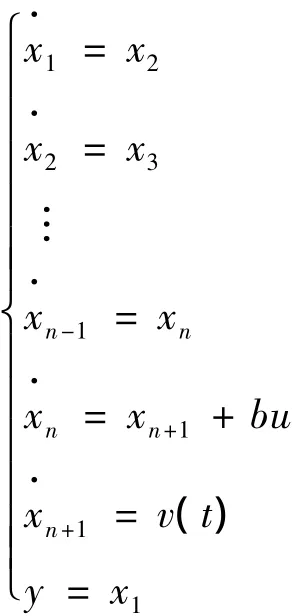
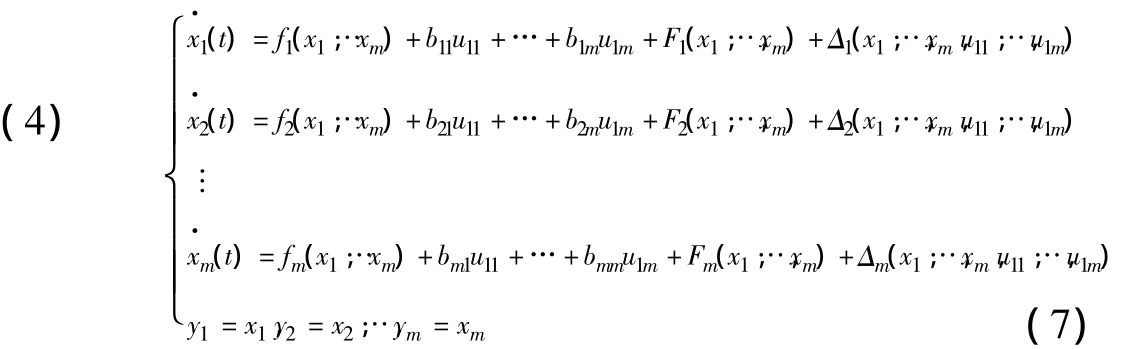
按式 （3）对扩张的系统建立扩张状态观测器

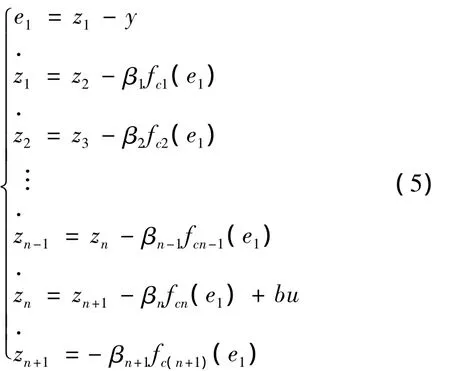
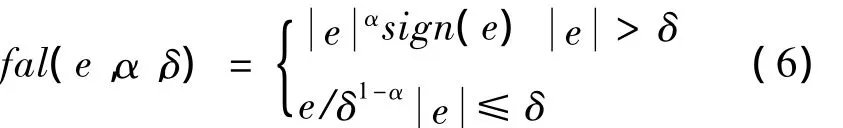
2.2 基于NESO的“系统扰动”估计

对于飞行控制系统等一类多输入多输出放射非线性系统，若系统标称模型已知，“系统扰动”可能为系统的参数变化、干扰输入或不确定性，则可基于NESO来估计多变量系统的“系统扰动”。假定:

只要适当的选择参数 β1，β2，…βn，βn+1，这个系统也能很好的估计系统 （4）的状态变量以及被扩张的状态变量，即满足:

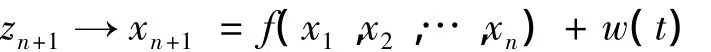
状态xn+1称被扩张状态。可以看出ESO是一种基于输出误差校正的状态观测器 （Extended state observer，ESO），它不仅给出控制对象的状态量，还可以估计不确定性模型和扰动总和的实时值，实时值即为扩张状态。根据输出误差的线性和非线性误差校正方式，扩张状态观测器分为线性扩张状态观测器 （Linear extended state observer，LESO）和非线性扩张状态观测器 （Nonlinear extended state observer，NESO）两种。式 （5）中，若取fci（ei）=e1，则 （5）为LESO，若取函数fal（e，α，δ）作为非线性函数fci（e1）的一般形式 （6），则（5）为 NESO［7－8］。

是m输入－m输出的系统，控制量的放大系数bij

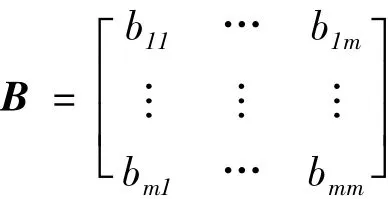
为已知的状态变量的函数且可逆，f=［f1f2… fm］为已知的非线性函数，Fi（x1，…，xm，uf）为由系统的参数变化、干扰输入引起的对第i个状态量的未知扰动量，Δi（x）为未知不确定性对第i状态量的影响。记

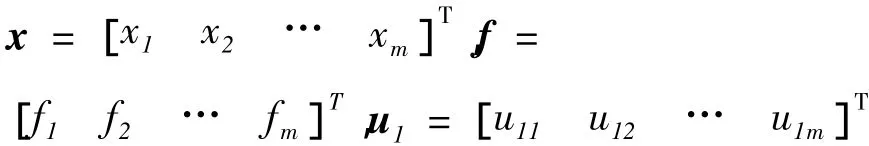
并引入“虚拟控制量”U=B u1。系统方程（7）变为

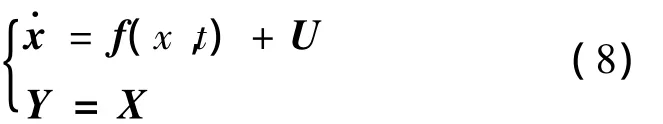
系统中第i个通道的输入输出关系为:

如果该通道上没有任何不确定性和干扰，则zi2→0;一旦该通道上存在不确定性和干扰，则zi2的估计值表示该通道上扰动值的总和的大小。式 （11）的离散形式为:

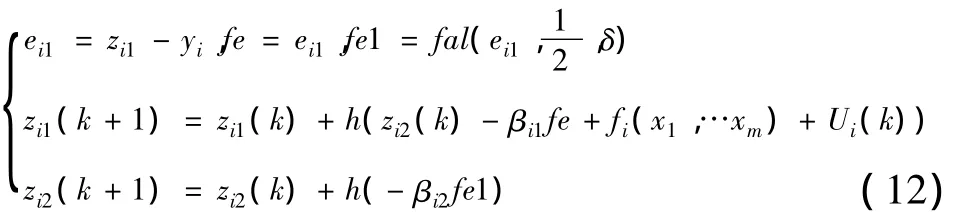
基于扩张状态观测器的扰动估计原理如图5所示。

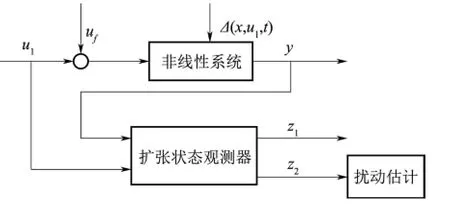
图5 基于扩张状态观测器的扰动估计Fig.5 Disturbance estimation based on NESO

2.3 基于NESO的补偿控制器设计

根据扩张状态观测器的原理，基于NESO的补偿控制器的设计如下。

扩张状态zn+1→g（x）uf（t）+Δ（x），则补偿控制律为:

加入补偿控制后，定义ξ=g（x）uf（t）+Δ（x）－zn+1，闭环系统方程变为:加入补偿控制后的系统和扩张状态观测器一起构成的整个闭环系统为:

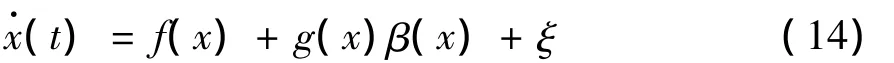
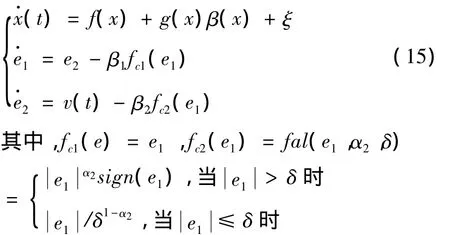
v（t）为假设的扩张状态的导数。

可以证明［4］，在新型强鲁棒自适应控制器构型下，当系统没有受到“系统扰动”的干扰时，只要设计的主控制器+被控对象组成的闭环系统是稳定的且具有工程要求的性能。而当系统中出现扰动时，补偿控制器输出的补偿控制信号加入系统后，在主控制器和补偿控制器共同作用下，可保证在闭环系统稳定，且具有良好的性能。

3 高超声速飞行器新型强鲁棒自适应控制器设计

在新型强鲁棒自适应控制器设计中，主控制器可采用成熟的控制方法来设计，本文采用PID控制器。首先利用小扰动线性化方法得到高超声速飞行器纵向通道线性化模型，列写如下:

状态空间表达式:

选取合适平衡点，确定在平衡点上的模型参数，针对每个确定的模型设计相应的PID控制器。

根据标准弹道，可以确定高度h=45345m时，攻角α=40°，飞行速度V=2433m/s，侧滑角为β=0°，倾侧角γs=0°，可得到此时的简化模型为:

针对高超声速飞行器特点，其姿态控制系统采用内外环控制系统结构。选取PID控制器结构如图6所示。

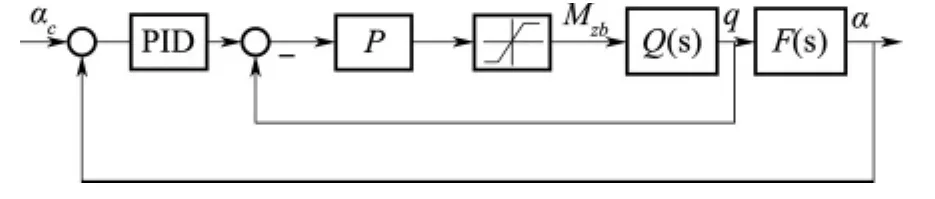
图6 纵向PID控制结构图Fig.6 Longitudinal PID controller

对于补偿控制器的设计，采用基于NESO的扰动估计器设计和补偿控制器设计，其控制器结构如图7所示。

a）首先，选取弹道上某特征点:飞行高度45345 m，飞行速度2433 m/s，针对线性模型的攻角指令为单位阶跃信号，针对非线性模型的攻角指令为40°～38°的阶跃信号。

b）主控制器参数:

根据PID控制器参数理论设计结果和实际仿真效果，进行适当调整之后，确立PID控制器参数为:KP=150，KI=3，KD=50。内环反馈控制增益K=30。

c）NESO参数:

根据NESO理论给出的经验参数和实际仿真效果，确立NESO 参数为:β1=300，β2=800，a=0.25，δ=0.0025。

d）补偿控制器参数:补偿控制律为:ucf（t）=－z，z由NESO估计得到。33

4 仿真结果及分析

（1）对线性化模型的仿真验证

纵向小扰动线性化模型的参数不拉偏情况下，利用PID主控制器的控制效果如下:

考虑将俯仰力矩系数Cm拉偏30%，考察PID控制器和PID+NESO控制器的效果如图9。

仿真结果表明，在正常情况下，PID控制器具有较好的控制效果，基本没有超调和稳态误差，但在模型参数进行一定程度的拉偏之后，仅采用PID控制器的控制效果变差，出现了较大的超调和震荡，而采用PID+NESO的新型强鲁棒自适应控制器较好的改善了控制效果。新型强鲁棒自适应控制器对于参数偏差等具有强鲁棒性。

（2）对纵向非线性化模型的仿真验证

特征点、控制器设定如上，面向非线性模型进行仿真，考察控制器性能。

纵向非线性模型的参数不拉偏情况下，利用PID主控制器的控制效果如图10。

将俯仰力矩系数拉偏30%，利用PID控制器和PID+NESO控制器的控制效果如图11。

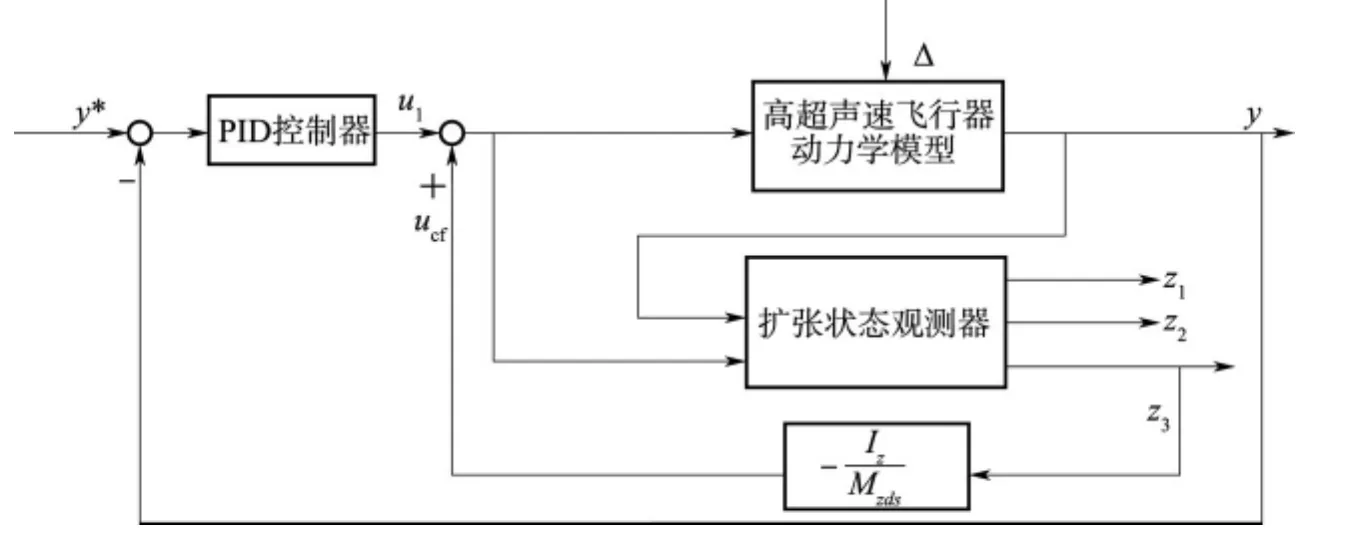
图7 基于NESO新型强鲁棒自适应控制系统Fig.7 The scheme of novel strength robustness adaptive controller based on NESO

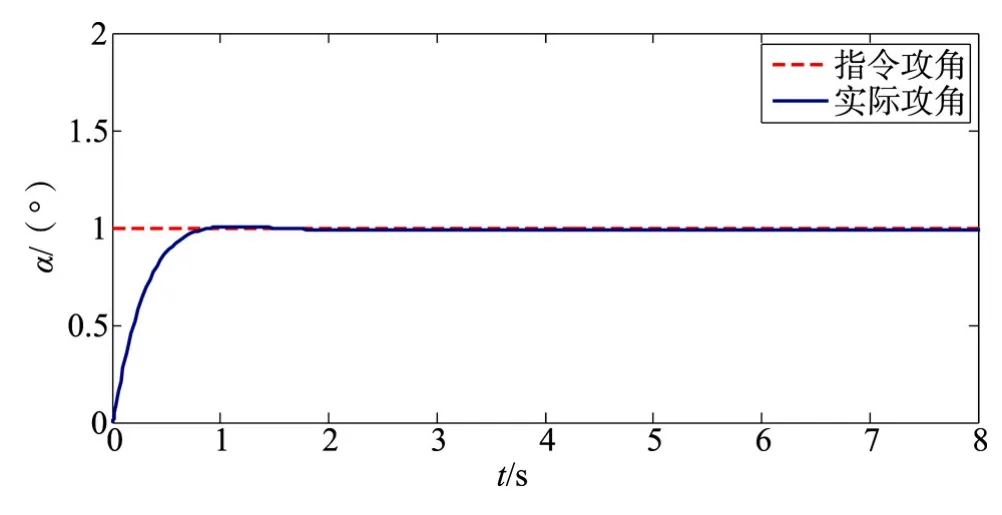
图8 在参数不拉偏情况下，PID控制器用于线性模型的攻角跟踪图Fig.8 The PID controller for the linear model of angle of arrack when parameter does not bias

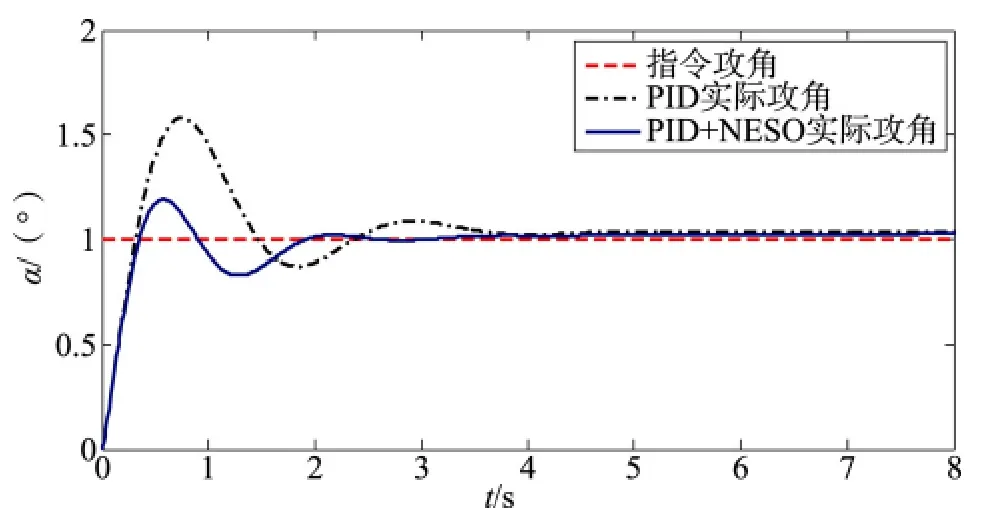
图9 在参数拉偏情况下，PID+NESO控制器用于线性模型的攻角跟踪图Fig.9 The PID+NESO controller for the linear model of angle of arrack when parameter bias

（3）跟踪全程攻角制导指令的仿真验证

为了验证新型强鲁棒自适应控制器的控制效果，对于高超声速飞行器再入返回飞行过程中的全程弹道制导指令，考察飞行器高度从70km到25km下降过程中对制导攻角指令的跟踪情况，其攻角指令由40°变为10°。

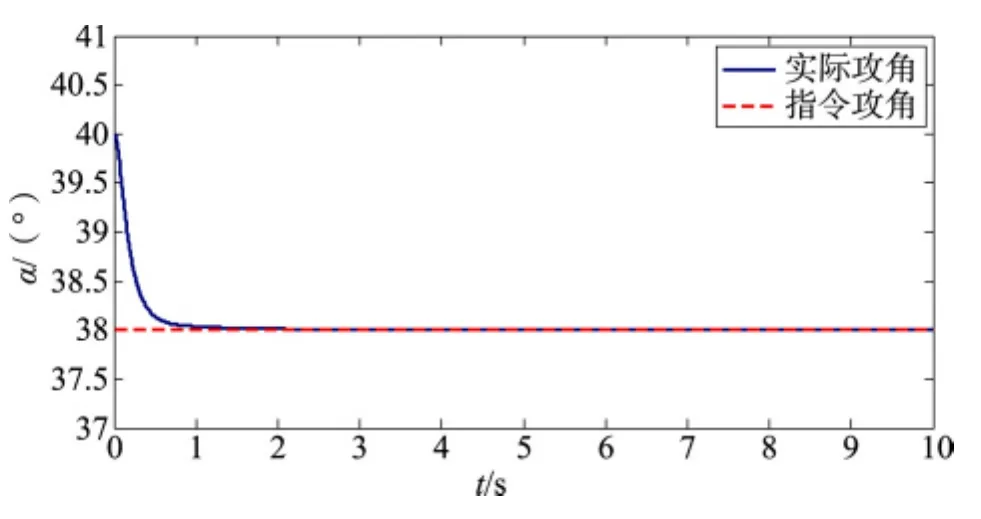
图10 在参数不拉偏情况下，PID控制器用于非线性模型的攻角跟踪图Fig.10 The PID controller for the nonlinear model of angle of arrack when parameter does not bias

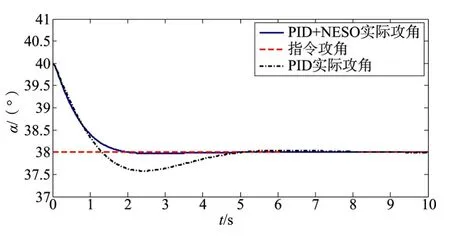
图11 在参数拉偏情况下，PID控制器和PID+NESO控制器用于非线性模型的攻角跟踪图Fig.11 The PID and PID+NESO controller for the nonlinear model of angle of arrack when parameter bias

首先，在参数不拉偏情况下，仅采用PID控制器和采用PID+NESO控制器的全弹道制导指令跟踪图如下所示，图11和图12是全弹道中攻角指令随时间变化情况以及跟踪效果，图13和图14是攻角指令随高度变化情况以及跟踪效果:

由以上仿真结果可见，仅采用PID控制器，在飞行器攻角建立过程中会有较大超调和一定的震荡，而采用PID+NESO控制器，减小了超调，基本消除了震荡。在之后的过程中，两种控制器都可以获得较好的跟踪效果。

其次，将俯仰力矩系数拉偏30%，仅采用PID控制器和采用PID+NESO控制器的全弹道制导指令跟踪图如下所示。其中，图15和图16是全弹道中攻角指令随时间变化情况以及跟踪效果;图17和图18是攻角指令随高度变化情况以及跟踪效果。

图16 参数拉偏采用PID控制器的制导指令随时间变化跟踪图Fig.16 The PID controller for the guidance command with time when parameter bias

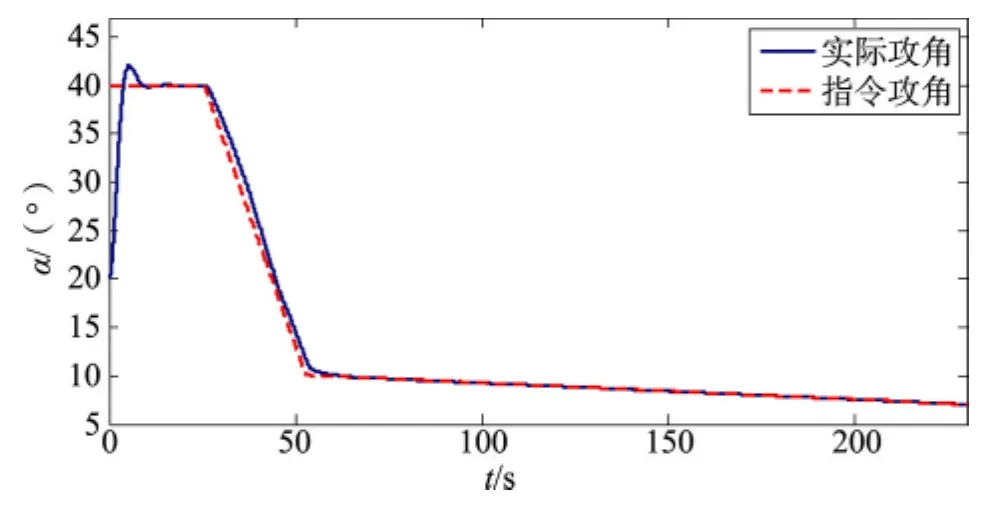
图12 参数不拉偏采用PID控制器的制导指令随时间变化跟踪图Fig.12 The PID controller for the guidance command with time when parameter dose no bias

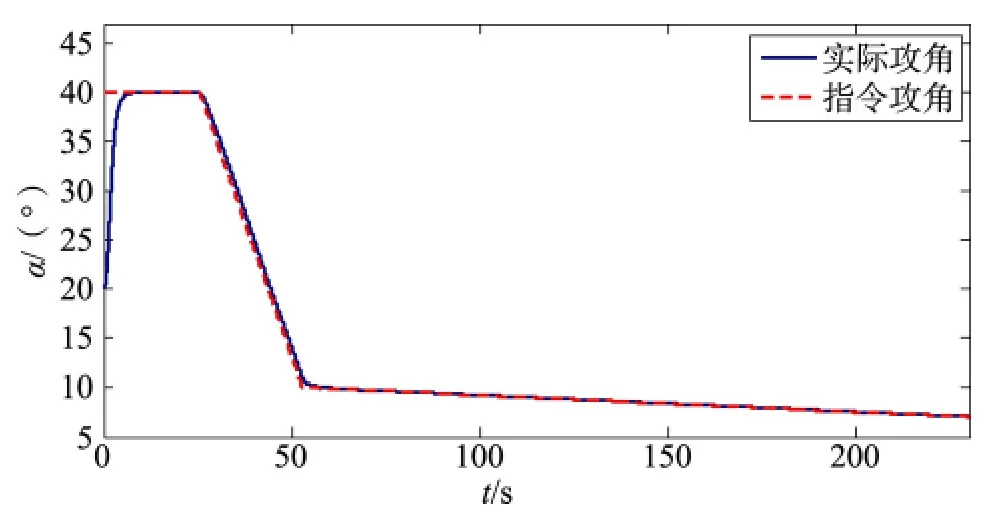
图13 参数不拉偏采用PID+NESO控制器的制导指令随时间变化跟踪图Fig.13 The PID+NESO controller for the guidance command with time when parameter dose no bias

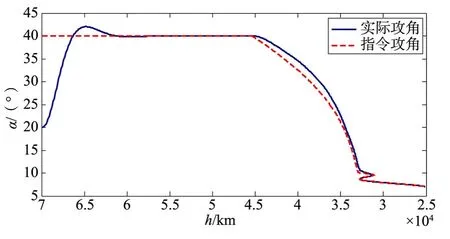
图14 参数不拉偏采用PID控制器的制导指令随高度变化跟踪图Fig.14 The PID controller for the guidance command with altitude when parameter dose no bias

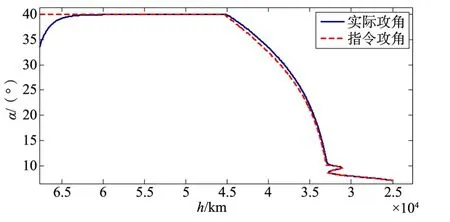
图15 参数不拉偏采用PID+NESO控制器的制导指令随高度变化跟踪图Fig.15 The PID+NESO controller for the guidance command with altitude when parameter dose no bias

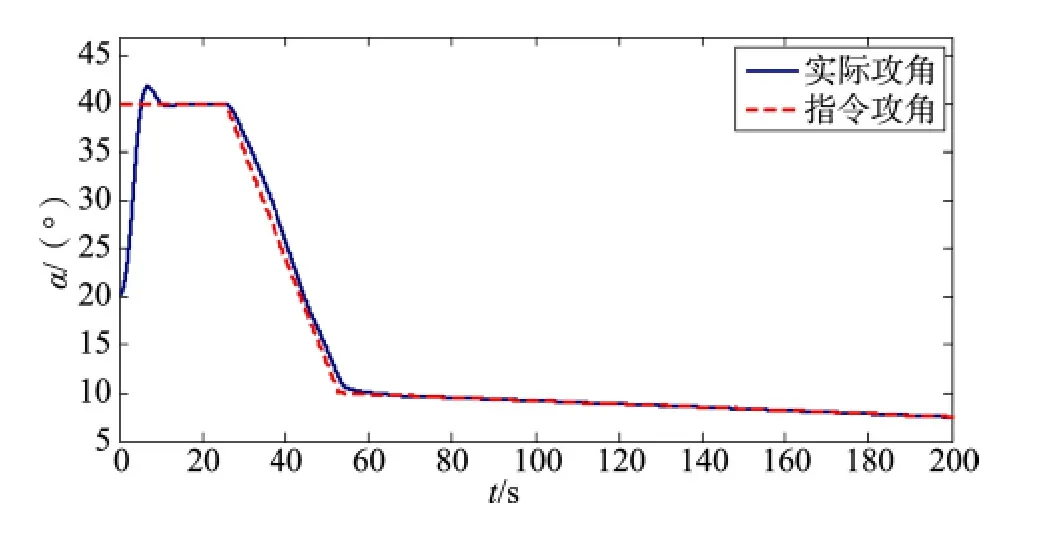
图17 参数拉偏采用PID+NESO控制器的制导指令随时间变化跟踪图Fig.17 The PID+NESO controller for the guidance command with time when parameter bias

由以上仿真结果可见，仅采用PID控制器，由于参数偏差的影响，在整个仿真飞行过程中，实际攻角对指令攻角的跟踪效果较差;而采用PID+NESO控制器，在仿真开始阶段有一定的超调，而在其它仿真飞行阶段仍然具有较好的跟踪效果。说明PID+NESO的新型强鲁棒自适应控制器克服了参数偏差所带来的影响，具有较好的鲁棒性。

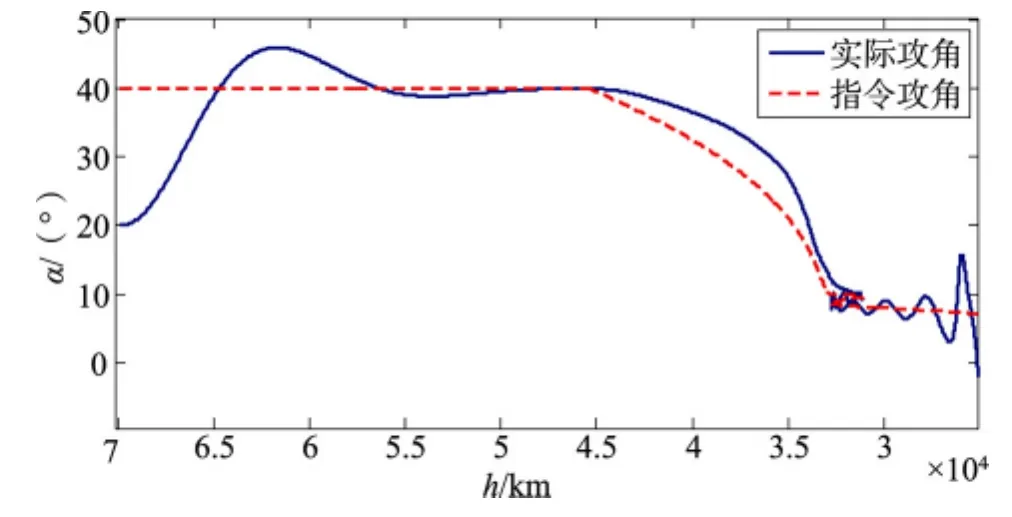
图18 参数拉偏采用PID控制器的制导指令随高度变化跟踪图Fig.18 The PID controller for the guidance command with altitude when parameter bias

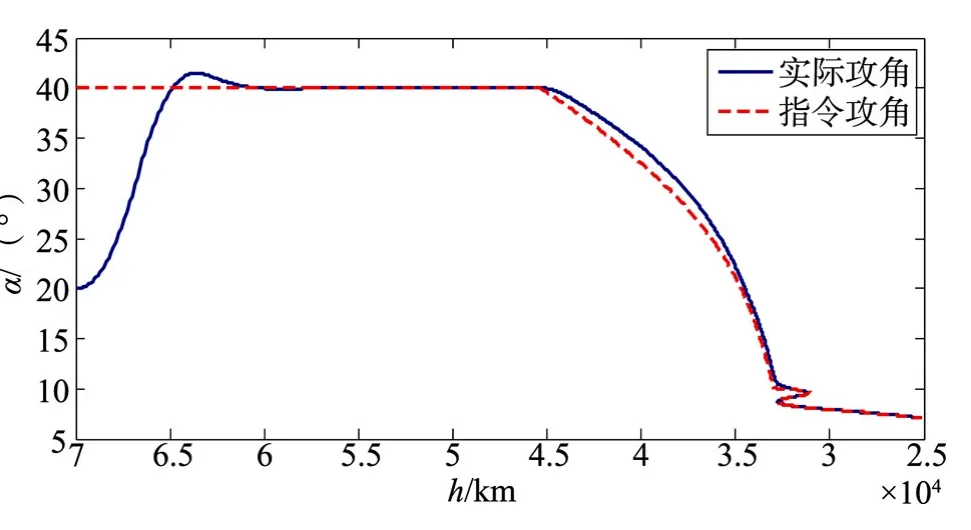
图19 参数拉偏采用PID+NESO控制器的制导指令随高度变化跟踪图Fig.19 The PID+NESO controller for the guidance command with altitude when parameter bias

5 结论

本文通过分析高超声速飞行器的特点，将自适应控制技术和鲁棒控制方法相结合，提出一种新型强鲁棒自适应控制器构型。在此构型的基础上，采用非线性扩张状态观测器来估计因大空域、高动态飞行带来的系统参数大范围剧烈变化、严重不确定性以及内、外部强烈干扰所形成的“系统扰动”。通过设计合适的补偿控制器，对“系统扰动”进行补偿。在主控制器和补偿控制器的共同作用下，不仅可保证整个闭环系统稳定，且可使闭环系统满足工程要求的性能。仿真结果表明，新型强鲁棒自适应控制器对于参数偏差的影响具有强鲁棒性。同时，新型强鲁棒自适应控制器分为主控制器+补偿控制器，且主控制器、补偿控制器可分开设计，这种设计思路具有广阔的工程应用前景。

［1］李智斌，李果，王大轶等．近空间飞行器动力学与控制的研究现状及难点［C］．动力学与控制及航天应用论文集．北京，中国，2008:120－142．［LI Zhi－bin，LI Guo，WANG Da－zhi．Present situation and problems of near space vehicle dynamics and control［C］．The dynamics and control of space application，Beijing，2008，120 －142．］

［2］Zhou Keming;Ren Zhang．A new controller architecture for high performance，robust，and fault－ tolerant control［J］．IEEE Transactions Automatic Control．2001．46（10）:1613 －1618．

［3］王伟．新型鲁棒容错控制方法研究［D］．北京:北京航空航天大学博士学位论文，2009．［WANG Wei，Resarch on A New Robust Fault－tolerant Control Method［D］．Beijing，Doctoral Dissertation of Beihang University，2009．］

［4］Wang Wei，Hameed Tahir，Ren Zhang．Extended State Observer－based Robust Fault－tolerant Controller for Flight Control Surface Failures［C］．The Proceeding of 9th International Conference on Electronic Measurement ＆ Instruments（ICEMI’09）．Beijing，2009:610－615．

［5］王伟，陈璐璐，任章．一种新型鲁棒容错控制器在飞控系统中的应用 ［J］．系统仿真学报．2011，23（1），104－107．［WANG Wei，CHEN Lu － lu，REN Zhang．Application of New Robust Fault－ tolerant Controller in Flight Control System ［J］，Journal of System Simulation，2011，23（1）:104 －107．］

［6］韩京清．自抗扰控制技术 ［M］．北京:国防工业出版社，2008． ［HAN Jing－qing．Active Disturbance Rejection Control Technique［M］． Beijing， National Defense Industry Press，2008．］

［7］黄一，韩京清．非线性连续二阶扩张状态观测器的分析与设计［J］．科学通报，2000，45（23）:1373－1379．［HUANG Yi，HAN Jing－qing．Analysis and design of continuous two order extended state observer of nonlinear ［J］．Chinese Science Bulletin，2000，45（23）:1373 －1379．］

［8］李菁菁;任章;曲鑫．机动滑翔飞行器的自抗扰反步高精度姿态控制［J］．系统工程与电子技术．2010，32（8）:1711－1721．［LI Jing－jing，REN Zhang，QU Xin．Design of active disturbance rejection backstepping attitude controller for maneuvering glide vehicles ［J］．Systems Engineering and Electronics，2010，32（8）:1711 －1721．］