浅析大惯量负载对机电舵系统的影响

徐方洁，李四保，谢劲松

(北京自动化控制设备研究所，北京100074)

0 引言

舵系统是导弹控制系统的执行机构，其性能的好坏直接影响导弹的性能。随着导弹飞行速度进一步提高，舵系统在高空稀薄空气下需要进行大舵偏机动，而在低空需要克服强烈的气动加热和大气动扭矩，舵面负载转动惯量势必增加，这对舵系统提出了更高的控制要求。负载转动惯量的增加对系统动态品质及稳态性能影响明显，严重时诱发系统产生极限环振荡，因此有必要研究大惯量负载对机电舵系统的影响，以提高舵系统自身的控制特性，满足控制总体需求。本文研究了大惯量负载机电舵系统的组成及基本原理，建立了电机—传动机构—负载的三质量模型，分别从理论及仿真二方面分析了惯量负载对舵系统的影响，通过试验验证了模型建立的有效性，理论分析与仿真结果的正确性。

1 大惯量负载机电舵系统组成及基本原理

某机电舵系统由舵机控制器、功率驱动电路、永磁无刷直流电机(BLDCM)、传动机构和反馈电位计等五大部分组成，结构组成如图1 所示。其中传动机构由一级齿轮副、一级滚珠丝杠副、连杆及输出轴组成。

机电舵系统的工作过程如下:舵机正常工作时，舵机控制器接受制导计算机给定的舵机输出轴偏转指令，驱动伺服电机带动舵面偏转，同时舵机控制器实时采集实际的舵机输出轴角度，保证舵面在一定的响应时间内以一定的精度趋近给定角度值。控制器采用高速PWM 调速模式，通过调整PWM 的脉冲宽度，实现对输出电压平均值的控制，从而达到通过控制电机的电枢电压来实现舵机调速。当实际舵机输出轴偏角与舵指令间存在误差时，控制器产生PWM 信号，PWM 信号经过驱动器进行功率放大后，驱动伺服电机转动。伺服电机输出的力矩通过传动机构到达舵机输出轴，带动舵面按照输入指令角度偏转;角度误差为正时，给出伺服电机正转的信号，舵面向正方向转动;角度误差为负时，给出伺服电机反转的信号，舵面向负方向转动，从而不断地调整角度，形成位置闭环系统。

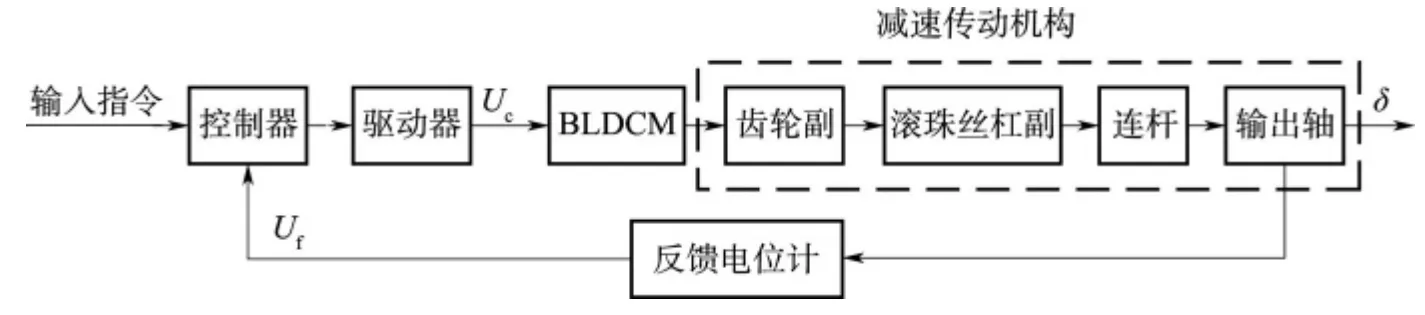
图1 机电舵系统组成框图Fig．1 The scheme of EMA system

2 大惯量负载机电舵系统模型搭建

在大惯量负载机电舵系统中，我们关注系统的内在控制特性，特别是稳态附近的小信号特性，因此不能将电机与负载看成一体，否则就是一个简单的刚体运动。对于实际系统，即便电机与负载是直接耦合的，但传动本质上是弹性的，在电机驱动力矩的作用下，传动机构会产生某种程度的弹性变形。对于加速度要求大，快速性和精度要求高的系统或是转动惯量大、性能要求高的系统，弹性变形不能忽略。考虑传动机构的弹性变形，将舵系统广义的被控对象视为如图2 所示的由电机、传动机构及负载还有连接三者间的等效刚度所组成的三质量系统，其中假设静摩擦及库仑摩擦均忽略不计［1］。

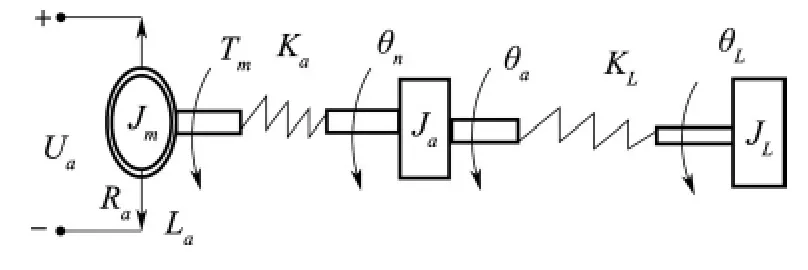
图2 电机-传动机构-负载三质量机电舵系统模型Fig．2 The three quality model of EMA on motor，driving mechanism and load

其中，Ua为电机某两相导通时的直流母线电压，Ra和La分别为电机绕组线电阻与等效线电感，Tm为电机的输出转矩，θn为电机经过传动机构减速器的输出转角，θa为舵机输出轴转角，θL为舵面负载的输出转角，Jm为电机的转动惯量，Ja为传动机构等效轴的转动惯量，JL为负载的转动惯量，Ka为传动机构等效轴的扭转刚度系数，KL为舵机输出轴与舵面连接轴的扭转刚度系数，在机电舵系统中，一般将舵反馈进行滤波、微分后进行前馈的速度补偿，位置控制器采用比例控制器，以形成双环控制，以此搭建的仿真模型如图3 所示:

图中，Ke为反电势系数，KT为电机转矩系数，α为反馈电位计反馈电压系数，Ca为传动机构弹性轴阻尼系数，2△为间隙宽度，ba为传动机构等效轴黏性阻尼系数，Ws(s)为PWM 控制与变换器的数学模型，bL为负载黏性阻尼系数，CL为舵机输出轴与负载舵面连接轴的阻尼系数，N 为减速比，各参数取值如表1 所示。

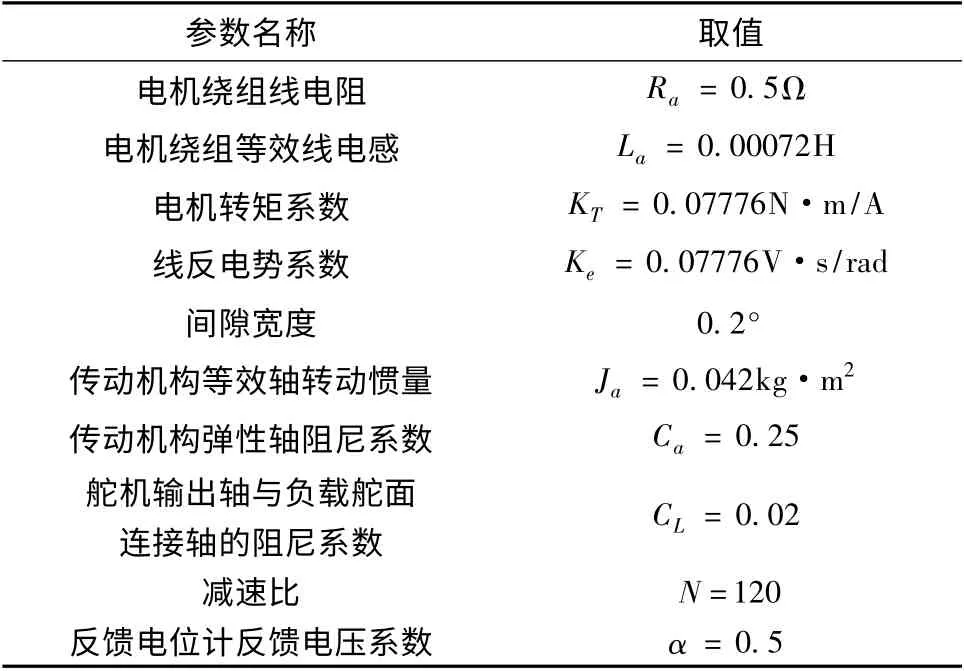
表1 机电舵系统各参数取值Tab．1 The value of all the parameters in EMA system

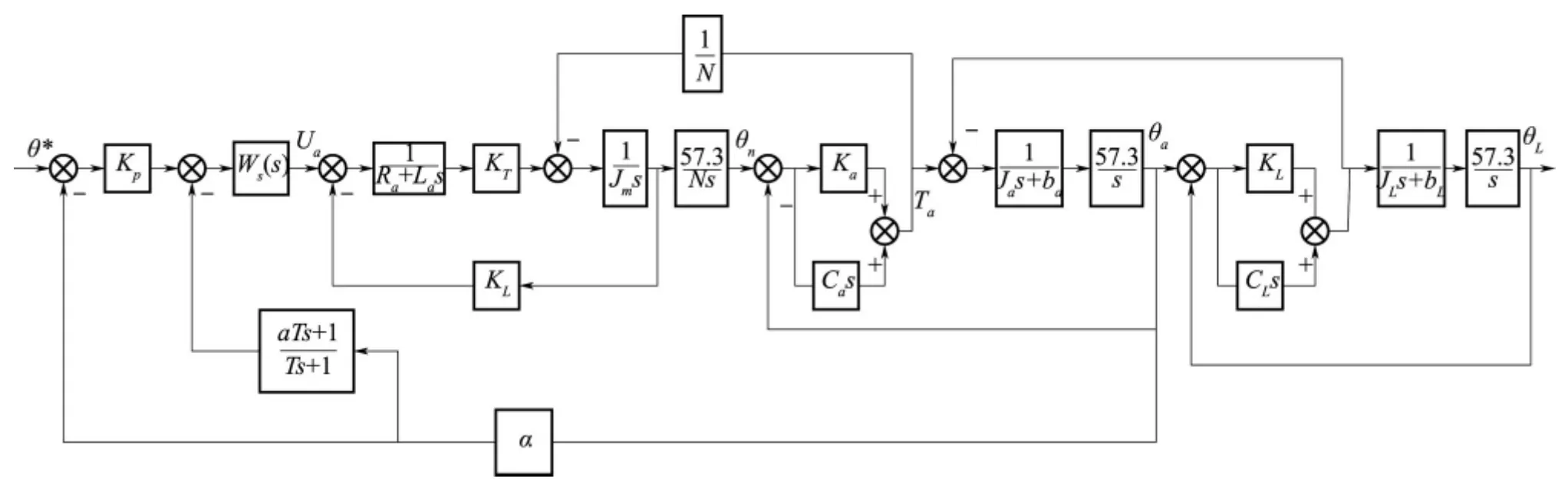
图3 电机-传动机构-负载的机电舵系统建模Fig．3 The model of EMA on motor，driving mechanism and load

3 理论分析及仿真验证

3.1 大惯量负载对机电舵系统的理论分析

根据控制系统设计，一般位置环在频率响应范围内希望得到如图4 (a)所示的开环波特图，其中ω2为位置开环过零分贝线的下限转折频率，它也是速度环开环截止频率，即= ω2。由于性能指标的要求，一般速度环过零分贝线的下限转折频率接近于高频谐振点ωr与反谐振点ωa。当速度环截止频率不变情况下，高频反谐振点ωa使速度环中频段下限频率减小，则在整定速度环时，速度环开环截止频率也减小，造成速度环相位裕量下降，进而影响位置环开环截止频率ωc，舵系统快速性下降，相对稳定性降低，如图4 (b)所示。同时，高频谐振峰值接近零分贝线时，速度环增益裕量下降，一旦越过零分贝线速度闭环将产生等幅振荡。

负载转动惯量的增加，使高频谐振点及反谐振点向复平面左侧移动，谐振峰值越接近零分贝线，将造成更大程度的幅值裕度削减，反谐振频率的降低，造成相位裕度的减小，故负载转动惯量的增加，对于双环舵系统而言，对速度环的稳定性影响更大［2］。

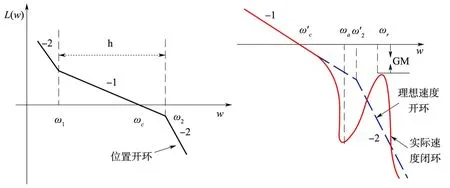
图4 负载转动惯量对位置环和速度环的影响示意图Fig．4 The scheme of the load inertial's impact on position loop and speed loop

3.2 大惯量负载对机电舵系统的描述函数分析法

非线性特性的描述函数法是非线性部件频率特性的一种推广，用来分析在无外作用的情况下，非线性系统的稳定性和自振荡问题，并且不受系统阶次的限制，一般都能给出满意的结果，因而获得了广泛的应用。

文中假设机电舵系统的电机、传动机构及控制器参数已经确定，研究负载转动惯量不同对舵系统造成的影响。按照描述函数法的分析方法，首先对图3 进行化简，如图5 所示。

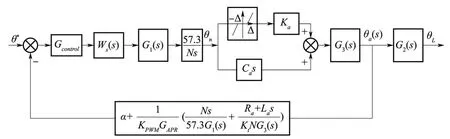
图5 描述函数分析法线性部分化简Fig．5 Simplification of the linear part about the describing function analysis method

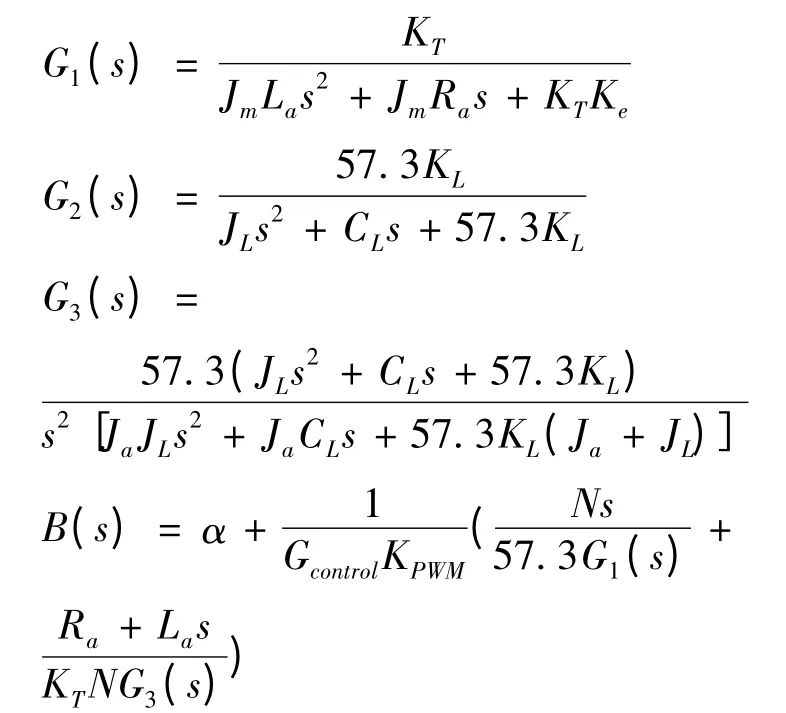
将间隙非线性等价为非线性环节NA，由θ*至θa的闭环系统的特征方程为:

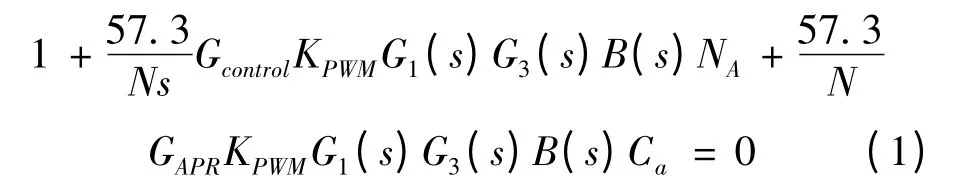
记

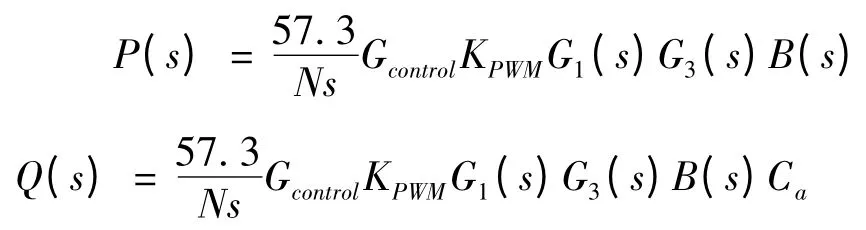
式(1)可以简化为

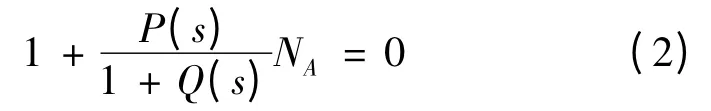
式(2)等价形式为

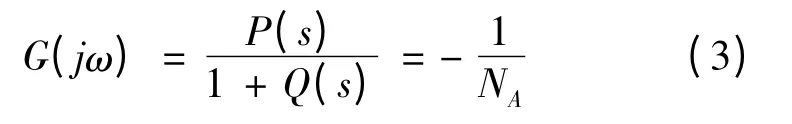
改变负载转动惯量，利用matlab 将线性部分的Nyquist 曲线与间隙的负倒描述函数画在同一复平面中，即可确定系统是否会产生振荡，描述函数分析结果如图6 所示。

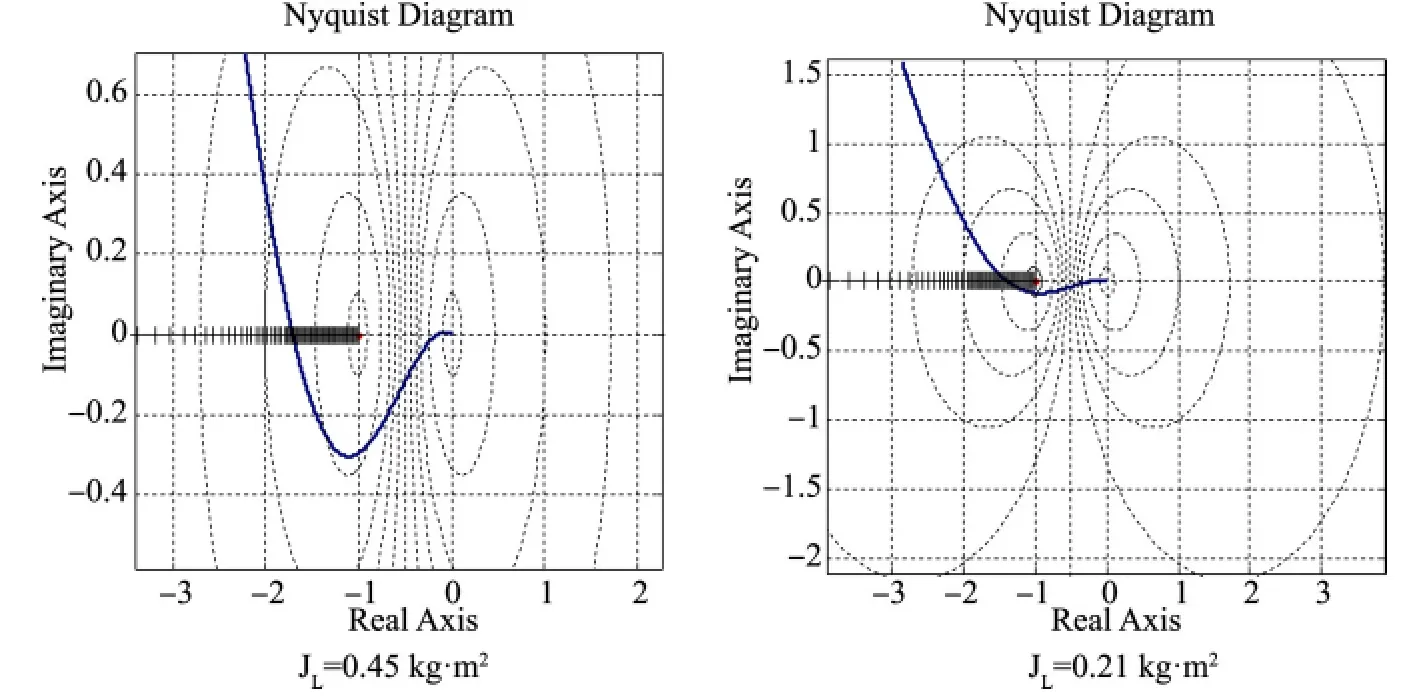
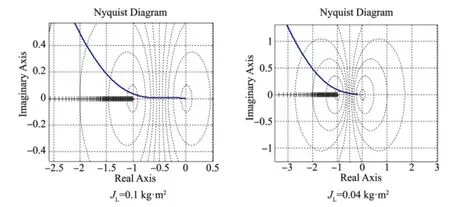
图6 负载转动惯量不同时，系统描述函数法示意图Fig．6 The scheme of the describing function method under different load inertial

从图6 可以看出，负载转动惯量为0.04kg·m2，0.1kg·m2时，由舵指令至舵反馈的非线性系统线性部分的频域特性与间隙的负倒描述函数间无交点。当负载转动惯量为0.21kg·m2，0.45kg·m2时，由舵指令至舵反馈的非线性系统线性部分的频域特性与间隙的负倒描述函数间存在交点，即非线性系统不稳定，而负倒描述函数随着振幅增加的方向由不稳定区进入稳定区域，交点对应着稳定的周期运动，对负载转动惯量0.45kg·m2处的交点进行计算，振荡频率约为157rad/s，幅值约为0.2V，描述函数法分析非线性系统与下一小节时域仿真结果相对应。

3.2 仿真验证

负载转动惯量不同时，对机电舵系统进行仿真分析，仿真结果如图7 所示。设置负载转动惯量分别为0.04kg·m2，0.1kg·m2，0.21kg·m2，0.45kg·m2四种情况，由于舵机输出轴与舵面连接轴刚度较强，故舵机输出轴响应与舵面响应基本类似。

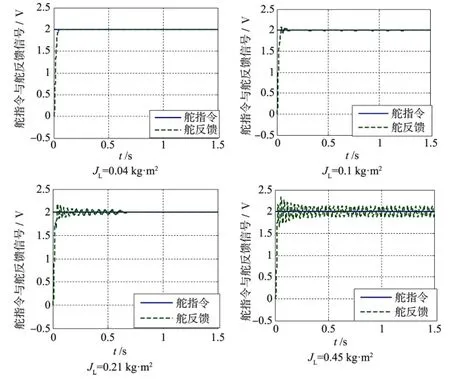
图7 负载转动惯量不同，机电舵系统阶越响应仿真曲线Fig．7 The simulation results of EMA system under different load inertial

仿真结果表明，随负载转动惯量的增加，舵反馈由较好地跟随指令到初期有几个振荡随后收敛于指令到呈现出等幅振荡，振荡程度愈加剧烈。为了验证模型搭建，理论分析与仿真的正确性，在某机电舵系统上进行了不同负载转动惯量的机电舵系统试验。

4 试验验证

通过在舵面负载上贴装不同厚度的质量块以改变转动惯量，分别对负载转动惯量为0.04 kg·m2，0.1 kg·m2，0.21 kg·m2，0.45 kg·m2四种情况进行了试验，试验结果如图8 所示。

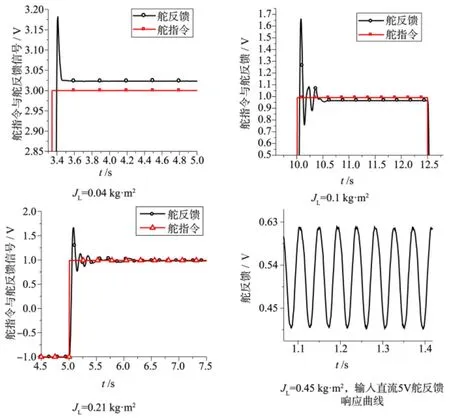
图8 负载转动惯量不同，机电舵系统阶越响应试验曲线Fig．8 The experiment results of EMA system under different load inertial

从图8 可以看出:对于某特定舵系统而言，一定负载惯量范围内，舵反馈响应初期出现几个振荡随后收敛于指令，但随负载转动惯量增加，调节时间变长，响应初期振荡个数增加，超调增加，但系统快速性能够达到性能要求。当负载转动惯量进一步增加，舵反馈出现了幅值一定、频率一定的极限环振荡。

5 结论

通过对大惯量负载机电舵系统的组成及基本原理分析，建立了电机—传动机构—负载的三质量模型，在模型基础上，从理论及仿真上分析了大惯量负载对机电舵系统动态品质及稳态性能的影响，并在某机电舵系统上进行了试验验证。结果表明:负载转动惯量的增加，会造成系统动态品质及稳态性能下降，严重时引起系统振荡，为后续改善系统动态及稳态性能，采取陷波滤波器及可调惯量比控制等控制方法提供了较强的理论依据。

［1］刘金琨. 先进PID 控制及其Matlab 仿真［M］. 北京:电子工业出版社，2005. ［Liu Jin-kun. Advanced PID control and Matlab simulation ［M］. Beijing:Electronic Industry Press，2005.］

［2］吴宇航，王占强，传动间隙对舰炮随动系统的影响研究［J］. 舰船科学技术，2009，31 (5):68-72. ［Wu Yu-hang，Wang Zhan-qiang. The research on the transmission backlash effect of gun servo system［J］.Ship science and technology，2009，31 (5):68-72.］

［3］胡寿松，自动控制原理［M］. 北京:科学出版社，2001. ［Hu Shou-song. The principle of automatic control［M］. Science Press，2001.］