接收机自主完好性监测技术研究
娄上月,辛 吉,洪诗聘,李建华,李 峰
(1.北京自动化控制设备研究所,北京 100074;2.空军驻某院军代表室,北京 100000)
0 引言
随着GPS导航技术应用领域的多样化,标准定位服务 (Standard Positioning Service,SPS)已无法满足用户对高精度、高可靠性的需求,这就需要对系统的定位精度、连续性、可用性和完好性有更加严格的要求。完好性是其中具有非常重要意义的指标之一,它是指卫星定位误差超过允许极限的时候,在一定时间内向用户发出告警的能力。从数学本质上来说,完好性就是对系统所提供信息正确性的置信度测量。
当前完好性监测的主要方法分为两种:一种是GPS完好性通道 (GPS Integrity Channel,GIC);另一种就是接收机自主完好性监测。RAIM由于其可以不依赖外部增强系统而独立工作,逐渐成为了完好性监测的主要工作方法和研究热点之一。
对于导航定位来说,完好性异常一旦发生所造成的后果是非常严重的,所以对完好性监测技术的研究是有其重要的安全意义和研究价值的。
目前国内对完好性监测的研究尚处于初始阶段,对完好性监测性能的综合研究非常少,与国外相比还存在一定的差距。本课题以最小二乘法对接收机自主完好性监测的基本公式进行了推导和分析,以奇偶矢量法在实际工程应用中验证了RAIM算法的正确性和可行性,并提出了一种新的故障卫星排除算法-RMS比较法,通过理论推导和实际工程反复验证了此算法的有效性。
1 最小二乘法进行卫星故障检测
传统的RAIM算法是利用冗余观测量来进行故障的检测和识别,主要有奇偶空间法、最小二乘残差法、距离比较法等。这里以最小二乘残差法为例,简介其检测原理。
GPS测量方程式如下所示:

式中x是4×1的位置矢量和钟差;y是n×1的伪距残差矢量;H为n×4阶观测矩阵,表示由各卫星到用户接收机的方向余弦矢量和含1的第四列构成的线性化矩阵;ε为n×1的测量误差矢量;n为观测卫星个数。
最小二乘估计的指标是:使观测量Z与其相应的估计值Hx之间的差的平方和最小。将该结果与y的作差,得到的结果为距离残差

矢量w:
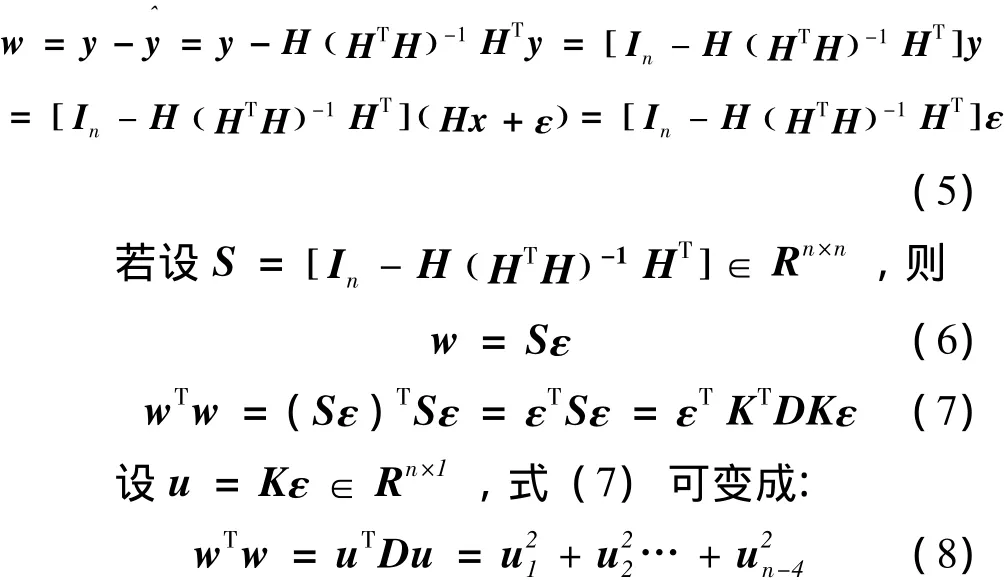
当ε~N(0,σ2),由于K为正交矩阵,u=Kε
0是关于ε的线性函数,则根据正态变量的线性变换不变性可知,u=Kε∈Rn×1服从均值为0,方差为Inσ20的正态分布。则根据χ2分布的概念可知,归一化变量满足自由度为n-4的χ2分布。

根据假设条件,当无故障卫星存在时,如果出现检测警告,则为误警,当误警率PFA给定时,可以确定检测门限值:

图1为MATLAB软件仿真出来故障检测效果图,数据来源是2011年3月28日在美国国家大地测量局 (National Geodetic Survey,NGS)专业网站上发布的GPS导航文件和观测文件,由于是真实的导航文件,其卫星并没有发生故障,所以为了验证最小二乘法正确性,人工在观测文件中加入了6个卫星故障,每隔200个历元加入一个,故障幅值为3σ,σ =4m。
2 奇偶矢量法进行故障检测
对于线性化GPS测量方程Z=HX+ε,若当前可见卫星中无故障星,则观测噪声ε~N(0,σ2)
0为白噪声误差;若当前可见卫星中存在故障星,则观测误差ε是包含噪声误差和故障误差的混合误差,满足方程Z=HX+ε+Tiq,其中Tiq表示第i颗可见卫星为故障星,T= [0 … 1 …0]T,故障幅值为q。因此可以将观测量Z转换到奇偶空间中,将观测误差提取处理,根据观测误差在有无故障情况下的不一致性进行故障检测。
若选择矩阵V满足 VH=0,则存在如下变换:
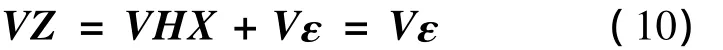
将满足条件的矩阵V称之为奇偶变换矩阵,则根据式 (10)可以发现,可以通过奇偶变换矩阵将观测误差提取出来进行一致性检测。
将矩阵H进行QR分解可以得到:



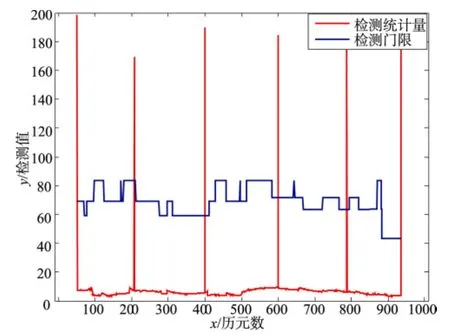
图1 最小二乘法故障检测图Fig.1 The scheme of fault detection by least square method
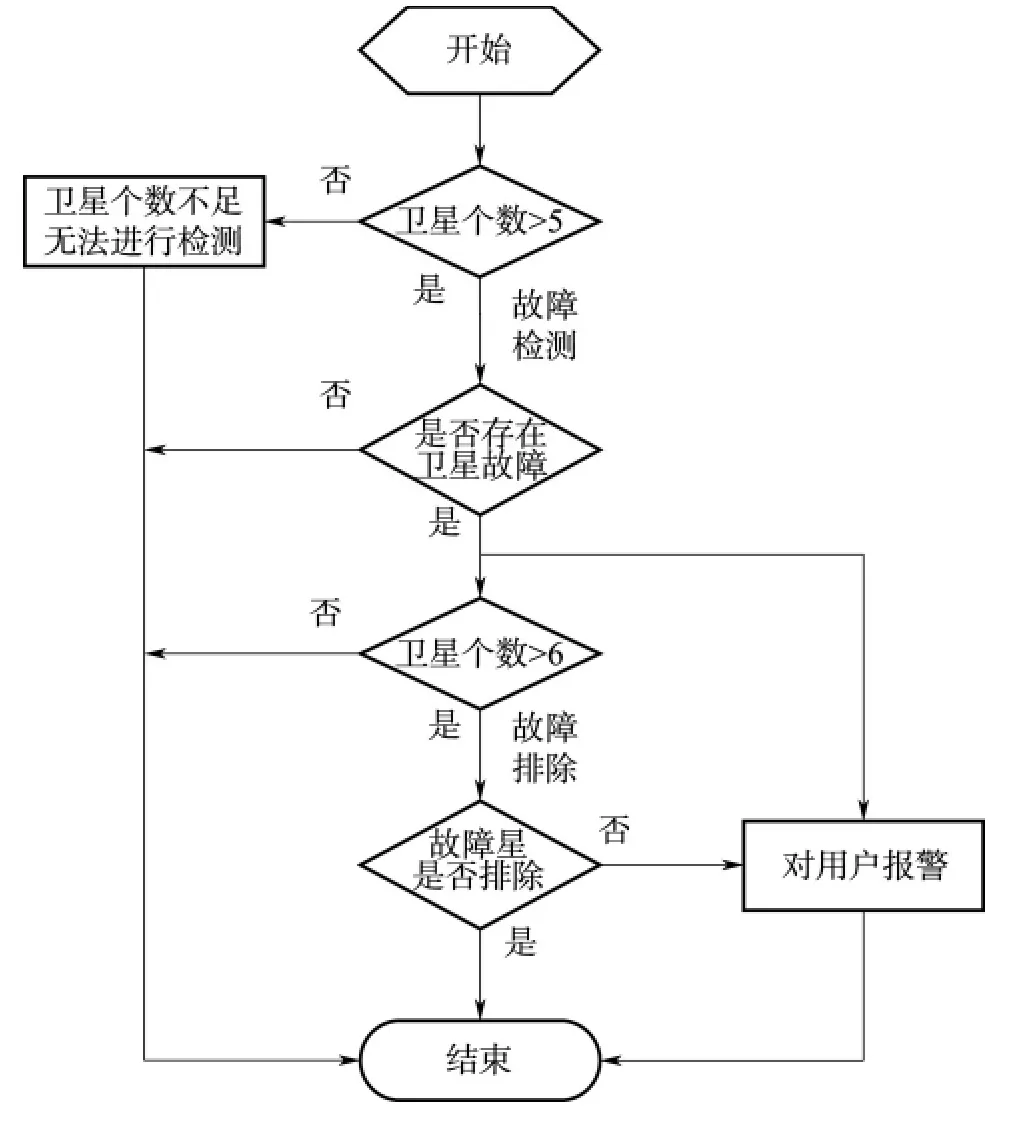
图2 RAIM算法检测流程图Fig.2 The flow chart of RAIM method detection
奇偶矢量法与最小二乘残差法在实际应用过程中具有等效性,但是由式 (6)和式 (14)进行比较可以发现,距离残差矢量w的计算需要多个矩阵相乘,而奇偶矢量p的运算只需要进行QR分解和一步矩阵相乘,所以奇偶矢量法具有更少的计算量,更能够满足高精度导航定位对TTA的要求;同时奇偶矢量法简单易懂,在实际工程中应用更为简便,是美国航空无线电技术委员会 (RTCA)推荐使用的算法。
使用MATLAB中的cputime()函数对奇偶矢量法和最小二乘法进行故障检测过程进行计时,选取其中2000个历元进行了事后处理,电脑的CPU主频为2.5GHz,其他所有检测条件均相同,其结果如下表:
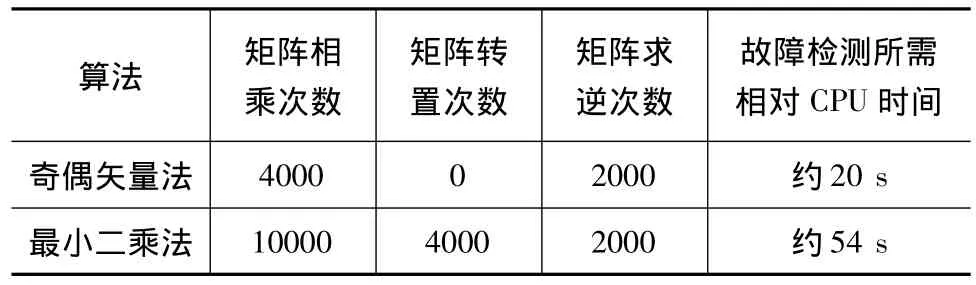
表1 两种算法的计算量比较Table.1 Contrast with calculation time of differrent algorithms
3 基于RMS比较法的单卫星故障排除
由于传统奇偶矢量法进行故障检测和排除是利用当前时刻的测量数据的统计特性进行相关计算,对冗余变量个数有严格要求,因此,该算法在冗余变量个数过少的情况下是不能高效率的完成卫星故障检测与识别的,极大的限制完好性监测性能,考虑到此算法在实际工程应用中的局限性,本文提出了一种新的故障识别算法——RMS比较法,即通过对当前全部观测量的伪距残差进行系列运算,识别并排除故障星。
RMS比较法具体实现流程:将每颗星伪距残差进行由大到小排序,而后从前到后每4个点计算一个残差的RMS值,如果卫星是n个,则得到n-3个残差RMS值。找出残差RMS最小的组合,求得该组合的平均值,此平均值作为故障识别的门限值,然后将每颗星的残差值与求得的平均值做比较,大于门限的卫星即是有故障的卫星。RMS比较法流程图如图3所示。
均方根体现的是数据趋近于均值的稳定性,RMS最小组合的均值应该是稳定性最好组合的均值,是最接近总体数据均值的,因此使用此均值作为门限应该是比较准确的。此算法的优点在于计算量小,单纯对伪距残差值进行排序比较,没有复杂的矩阵计算,在DSP程序运行过程中不会占用过多资源;简单易懂,实现容易,此算法可以算是传统距离比较法的简单运算,但是比之前算法更加精妙;不是使用冗余变量一致性进行运算,可以弥补传统算法必须在可见星大于6颗的前提下才能进行故障识别的缺陷,在可见卫星不足的极限情况仍能有效的进行故障排除,极大增强了完好性监测性能。
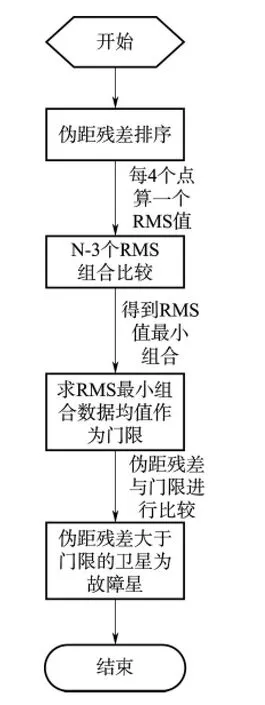
图3 RAIM算法检测流程图Fig.3 The flow chart of RAIM method detection
为了验证RMS比较故障识别算法的正确性,在常规单星故障情况和少星情况下,在第3颗可见卫星上人为加入脉冲故障,其故障识别检验结果如下:
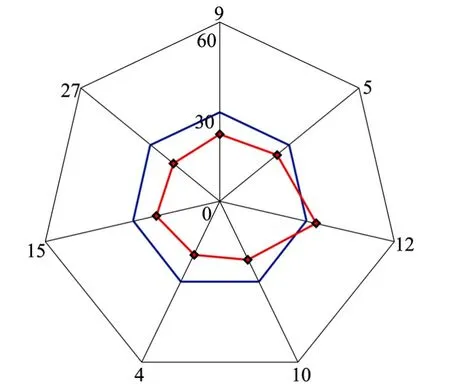
图4 在常规情况下RMS比较法进行故障排除Fig.4 The fault identification of RMS in common practice
图4为卫星故障识别图,图中横向圈线为刻度线,纵向分割线表示当前历元可见卫星号,红色点线表示每颗卫星对应伪距残差值,蓝色粗线表示RMS最小组伪距残差平均值,即排除算法门限值。由图中可以发现,第3颗卫星对应伪距残差值大于检测门限,可以判断当前历元第3颗可见卫星,即12号卫星为故障卫星,与仿真初始设置相同。
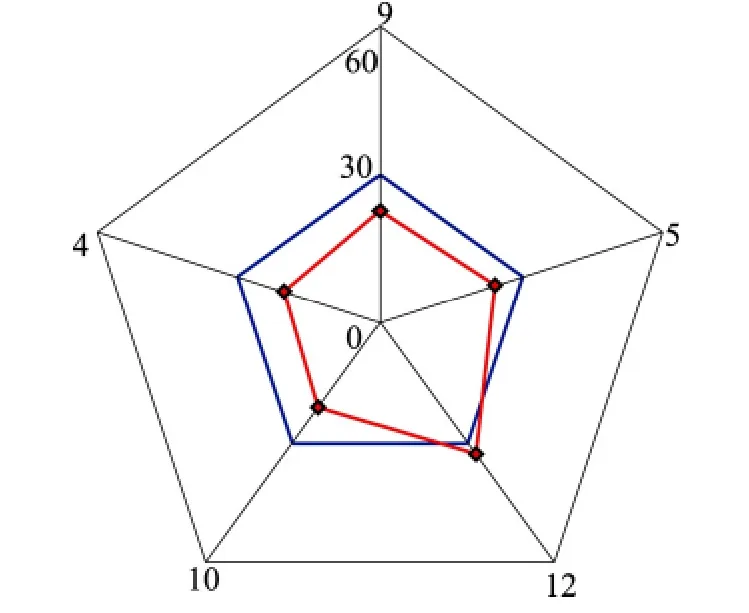
图5 在少星情况下RMS比较法进行故障排除Fig.5 The fault identification of RMS in few satellite
图5是在少星情况下进行的故障识别,人为限定选取历元可见卫星个数为5颗,在传统故障识别算法无法正常判断出故障卫星的情况下,RMS比较法仍然能够正常工作,并且正确识别出第3颗卫星为故障星,说明RMS比较法在故障识别过程中的优越性。
4 结论
本文从完好性监测的原理和本质出发,对传统RAIM算法进行了详细的公式推导并给出了仿真结果,对传统算法正确性进行了验证;对传统算法的优点和缺陷进行了深入的分析,考虑到传统算法在少星情况下无法正常进行故障检测与排除的缺陷,提出了一种新的故障排除算法——RMS比较法。在传统算法无法正常工作的少星情况下,该算法仍然能够正确识别并排除故障卫星,充分体现了算法的正确性和优越性,具有较强的工程应用价值。
[1]赵琳,李亮,程建华,娄上月.用于识别双星故障的RIAM算法[J].北京航空航天大学学报,2010,Vol.36 No.11:585-589.[Zhao Lin,Li Liang,Cheng Jian-hua,Lou Shang-yue.New RAIM algorithm for identifying simultaneous double-faulty satellites[J].Journal of Beijing University of Aeronautics and Astronautics,2010,Vol.36 No.11:1 -5].
[2]Young C L.Analysis of Range and Position Comparison Methods as a Means to Provide GPS Integrity in the User Receiver[C].Proceeding of ION 42th Annual Meeting,WA,USA,24-26,June 1986,pp:1-4.
[3]Parkinson B W,Axeled P.Autonomous GPS Integrity Monitoring Using the Pseudorange Residual[J].Navigation Journal of The Institute of Navigation,Summer 1988,35(2):255-274.
[4]Sturza M A.Navigation System Integrity Monitoring Using Redundant Measurement[C].Proceedings of the Third International Technical Meeting of the Satellite Division of the Institute of Navigation,Colorado Springs,CO,USA,19 -21 September 1990:437-443.
[5]郭睿,韩春好.接收机自主完好性监测的算法分析[J].测绘工程,2008,17(2):34-38.[GUO Rui,HAN Chunhao.Analysis of RAIM algorithm [J].ENGINEERING OF SURVEYING AND MAPPING.2008,17(2):34 -38.]
[6]Liang Li,Lin Zhao,Wei Cao and Shangyue Lou.A solution separation RAIM scheme based on adaptive clock-bias model[C].Proceedings of the 2010 IEEE International Conference on Information and Automation.June 20-23,Harbin China,pp:250-254.

