快速收敛的牛顿路径算法在交通分配中的应用

程 琳，孙 超,邵 娟

（东南大学 交通学院，南京210096）

快速收敛的牛顿路径算法在交通分配中的应用

程 琳*，孙 超,邵 娟

（东南大学 交通学院，南京210096）

以确定性交通网络用户均衡问题为研究对象，从理论上推导出以路径费用函数为基础的用户均衡模型，在这基础上，提出快速收敛的牛顿路径算法.该算法每次仅对一OD对进行牛顿型流量转移，转移完再更新道路流量，提出“更快速度接近均衡解原则”，运用这一原则来简化Hessian阵，从而得到迭代方向，并通过对原函数二阶泰勒展开式进行一维搜索，寻找出最优步长.将该算法运用于实际交通分配问题，分别对小、中、大三种网络类型进行测试.结果表明，相比于传统的梯度投影算法，快速收敛的牛顿路径算法具有更快的收敛速度和更高的精度，在迭代前期尤为明显.

交通工程；牛顿路径算法；优化步长；交通分配；简化方向

1 引 言

交通分配是城市交通建模系统四阶段中最后一个阶段，它是将每一个OD点对间预测的交通量分配到实际道路网中，并且要满足Wardrop第一原则（用户均衡准则）[1].在达到用户均衡状态时，同一OD对之间，所有使用路径的旅行时间相等且最小，所有非使用路径的旅行时间均大于等于使用路径的旅行时间，没用人能够通过单方面改变自己行驶路径的行为，来减少自己的旅行时间[2].

求解用户均衡交通分配问题，既可以用路段流量为变量，也可以用路径流量为变量来构建数学模型并求解算法.可行域为路段流量的算法称为路段算法，这类算法以直接求解路段交通量为目的，常用的算法有Frank-Wlofe算法[3]和限制单纯分解算法（RSD）[4].可行域为路径流量的算法称为路径算法，该类算法以直接求解路径交通量为目的，常用的算法有非集计单纯分解算法（DSD）[5]、梯度投影算法（GP）[6-8]、共轭梯度投影算法（CGP）[9]和投影梯度算法（PG）[10].除上述求解两类算法之外还存在另外一种交通流量分配方法，即起点算法（OBA）[11-12]，它的直接变量是从路段流入结点的流量比例，算法以求解起点通路比例为直接目的来间接获得使用路径的选择率和路径交通量，从这个方面看来，起点算法具有路径算法的特征.表1对比了三种算法，以便更好地理解三种算法之间的异同.

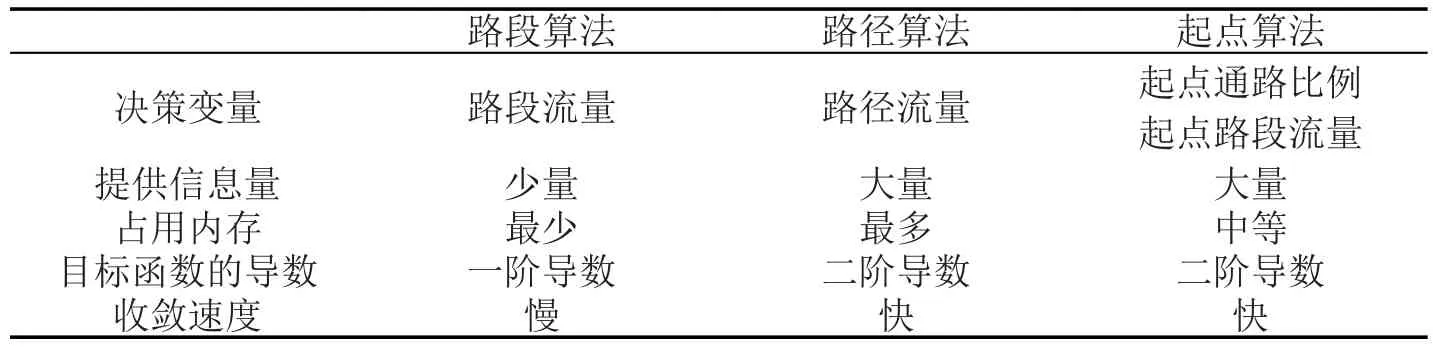
表1 路段算法、路径算法和起点算法的比较Table 1 The comparison of link-based algorithm,path-based algorithm and origin-based algorithm

1994年Jayakrishnan等人在求解交通分配问题时，提出了梯度投影（GP）算法[6].GP算法是一种快速收敛的路径算法，Chen A等研究发现GP算法的计算效率和收敛速度明显优于路段算法和DSD算法[13].但当GP算法接近最优值时，会产生震荡现象，这种现象造成该算法很难得到高精度的路径解[9].路段算法收敛精度较低，且不提供路径信息，起点算法原理复杂，应用性较差，路径信息需要后期的回溯，而路径算法收敛精度高，原理简单，路径信息完整，最具有应用前景，因而本文主要研究这类路径算法.

如果单独对算法的某一步骤进行优化，有两个方法可以解决上面的问题，第一是寻找更精确的迭代方向，即对Hessian阵的逆进行优化；另一种方法是寻找更精确的步长.目前GP算法中的Hessian阵假设路径之间相互独立，即Hessian阵为对角阵，显然这是不合理的，因为路径之间可能共享某个或某些路段，路径之间必然具有相关性.在GP算法中，步长的确定是从单位步长开始，按一个固定的系数进行递减，这样很容易产生刚开始步长太大，以致收敛过程中最优路径频繁进出使用路径集，产生许多重复、无效地计算过程；而在迭代后期，步长又过小，使得路径解不能快速收敛.本文所提出的快速收敛牛顿（RCN）算法同时解决了GP算法中存在的这两种问题.

GP算法在一次迭代循环过程中，同时计算所有OD对间的方向和步长，从而确定各OD对使用路径的转移交通量，然后同时进行交通量的转移.每个OD对都独立朝着自己使总目标函数减少的方向移动，这一过程会出现事与愿违的现象，总的目标函数并未减少，算法不收敛于最优解（比如步长取固定的牛顿经典步1）.这种整体转移流量方式不便于方向和步长的优化，因而GP算法需要进行整体优化来得到更快收敛、更高精度的路径解.因而本文的RCN算法采用了局部转移流量方式，提高了流量更新效率.

2 交通网络均衡模型

目前交通分配遵循用户均衡(UE)原则（没有用户能够通过改变自己的路径来获得更短的旅行时间）或者系统最优(SO)原则（路网总旅行时间最小）.以路段费用函数为基础，这两种分配原则下的目标函数可用式（1）、式（2）来表达.

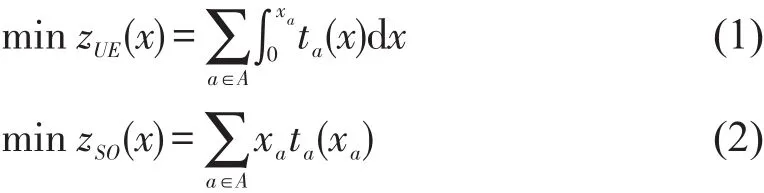
式中 xa表示路段a上的流量；ta(xa)表示路段旅行费用函数.

类比于路段费用函数SO模型，以路径费用函数为基础的SO模型是很容易表示的：.但至今学者们并没有提出以路径费用函数为基础的UE模型.从式(1)出发推导出UE原则下以路径费用函数为基础的目标函数.

aa非常直观的物理意义：它对路径求偏导即为路径费用，这对我们加强UE模型的理解很有帮助.孙超等[14]证明了式(4)与Wardrop第一原则等价性.

综上交通网络均衡数学模型的目标函数如表2所示.

表2 均衡网络流数学模型目标函数Table 2 Objective functions of equilibrium network model

3 快速收敛牛顿（RCN）算法

3.1 RCN算法原理

RCN算法把网络

上的交通流按OD对的不同分成不同的层，每次更新一个层上的流量而将来自于其他OD对上的出行看成是背景流量.每次迭代更新的目标是：在当前背景流量条件下，使来自当前OD对的用户路径选择趋于Wardrop原则，即就某个OD对而言，所有使用路径的出行费用不高于非使用路径的出行费用.图1形象地给出了RCN算法分层叠加的原理.RCN算法将交通分配过程按照出行分布的OD对分解成若干个子过程，若干个子过程在网络空间中叠加，就形成了交通网络上的路径流量.每个子过程只含有一个OD对，因而这些子过程的求解相对比较简单，牛顿法就是一个很好方法.

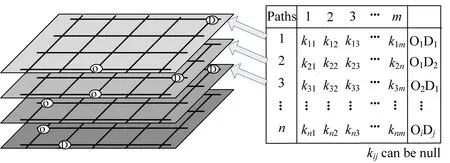
图1 快速收敛牛顿算法原理示意图Fig.1 The principle of RCN algorithm

算法的流程可以分成两个部分，即初始化和主循环.初始化操作的目的是先将OD交通量粗略地分配到交通网络中，为接下来的路径交通量转移奠定基础.进入主循环后，算法的主要工作是反复地进行使用路径集的更新和路径流量的转移，直到满足规定的精度条件或者达到最大循环次数.在每次循环的最后，需要对该OD对影响的路段流量进行更新，这一过程运用了最新的信息，使得方向和步长确定更加精确，从而大大提高了算法的精度；再通过选用简化的牛顿方向和优化步长，使得算法的迭代步数大幅度降低，从而整体上提高算法的运算速度.

正因为采用了每次仅对一OD对进行牛顿型流量转移，转移完就更新道路流量的方式，所以才可以使用更为精确的牛顿简化方向和优化步长.

（1）牛顿方向简化（Hessian阵的处理）.

根据最优化理论可以计算出牛顿下降方向为

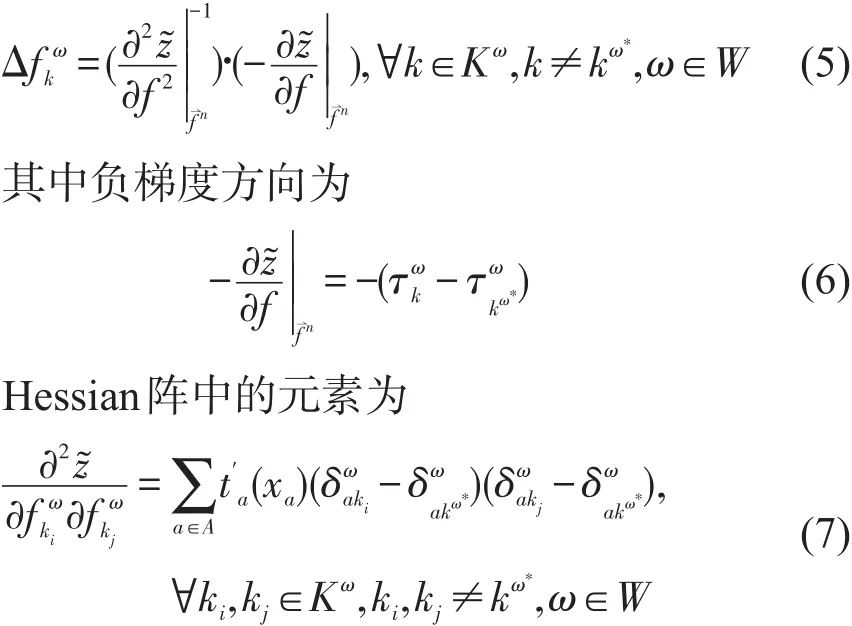
提出“更快速度接近均衡解原则”.在均衡状态下，对每个OD对ω而言路径费用是相等且等于路径最小旅行费用.在多次迭代后，每个OD对ω中，非最短路径费用的数值相差不大，因而负梯度方向的数值也几乎相等.为了更快地达到均衡状态（即)还是相等且等于路径最小旅行费用），非最短路径流量的增量（实际为负值）的大小应与路径费用增量有关，最终使得对每一OD对ω上，任意非最短路径费用增量相等.

根据上面提出的原则，运用式（8）可推出速度更快、更简洁的Hessian阵.

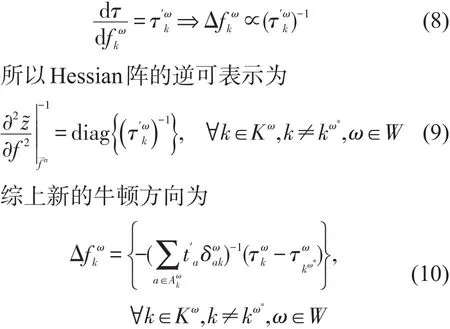
（2）优化步长.

由于前面Hessian阵的近似处理，因而需要一个优化的步长来进一步调整方向，以使算法能够更快、更好地收敛于最优点.目前所有路径算法步长均为在每次迭代过程中，所有OD点对使用同一步长.显然在一次迭代过程中，不可能每个OD点对的最优步长λω是一样的，最优步长总有差别.如果我们每次选择λω较小的，那么会使得收敛速度变慢；如果选择λω较大的，那么搜索范围会超出可行域，虽然可以用投影算法拉回来，但这种取法带来许多不必要的计算量.正因为如此，本文提出了多步长梯度投影算法，该算法可以大大降低原问题的迭代步数，使得算法能够更快、更好地收敛.

对式(4)以 fω为自变量进行二阶泰勒展开：

当然也可以对式(4)以x为自变量进行二阶泰勒展开，同样可以得到优化步长为：

式(15)与式(16)是等价的，虽然后者比较简单，计算速度快，但需要将Δf转换为Δx，这样需要给Δx分配新的内存空间.优化步长的寻找相当于一维搜索过程，关键在于用二阶泰勒展开式来代替原目标函数.经过测试发现，实际道路网络中每个OD对的使用路径绝大部分为一条，大于三条的非常少，式(15)就是对这有限的几条路径进行运算，运算量非常小.

（3）更新路径流量.

根据式(10)、式(15)中的方向和步长对路径流量进行更新.

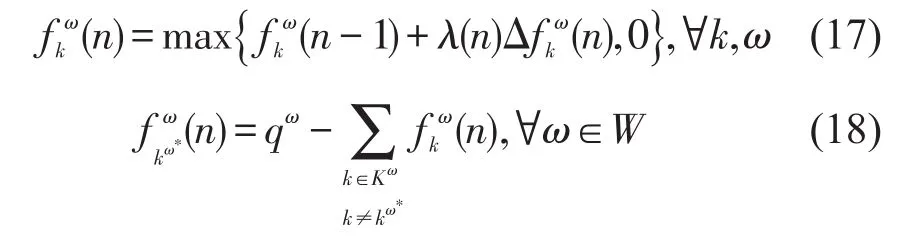
3.2 RCN算法步骤

RCN算法由初始化、列生成、求均衡解及收敛检验三个部分组成.初始化是为了生成每一OD对间的初始使用路径集合；列生成是为了在当前路段费用ta的基础上生成最短路径，若该路径是新生成的，则将之添加到使用路径集合中；求均衡解及收敛检验是为了在当前受限路径集中运用RCN方法求解主问题，并建议是否满足收敛条件，满足则停止计算，不满足则进入下一次循环当中.RCN算法的详细步骤如下.

（1）初始化.

Step 1xa=0,ta=ta(xa),∀a；Kω=∅；确定精度ε的值；计数器n=0.

Step 2选择一个未被选择过的OD对ω.

Step 3找出OD对ω的最短路kω∗(0)；确定初始使用路径集合Kω=Kω⋃kω∗(0).

Step 4全有全无加载，确定路径流量

Step 5更新路段流量

Step 6更新路段旅行时间ta(0)=ta[xa(0)],∀a.

Step 7如果已完成所有OD对的迭代更新，转至Step8；否则转至Step2.

（2）列生成、求均衡解、收敛检验.

Step 8计数器n=n+1.

Step 9选择一个未被选择过的OD对ω.

Step 10更新使用路径旅行时间(n),∀k.

Step 11找出最短路 kω∗(n).更新使用路径集合，如果Kω中不存在kω∗(n)，则Kω=Kω⋃kω∗(n)；否则将Kω中的最短路径标记为kω∗(n).

Step 12根据式(10)、式(15)计算方向和步长

Step 13计算旅行时间误差：

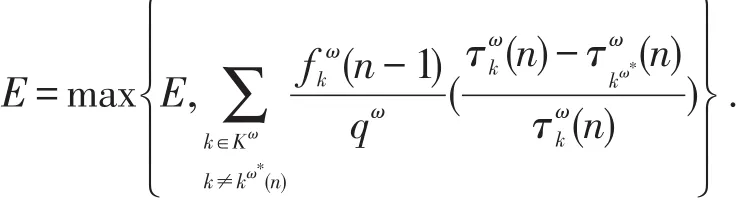
Step 14更新原使用路径流量

Step 15更新最短路径流量

Step 16如果=0，则Kω=Kωk.

Step 17更新路段流量 xa(n),∀a.

Step 18更新路段旅行时间 ta(n),∀a.

Step 19如果已完成所有OD对的迭代更新，转至Step 20；否则转至Step 9.

Step 20收敛检验，如果E≤ε,停止计算；否则转至（2）列生成、求均衡解、收敛检验过程.

4 计算实例及数据分析

本节采用三个交通网络（Nguyen[15]、Sioux Falls[16]、淮南市[17]）作为实例来比较GP算法和RCN算法的收敛速度和精度，三个交通网络的规模如表3所示.在一台Intel(R)Core(TM)2 Duo CPU E7500 2.93GHz的计算机上分别编制了GP算法和RCN算法的C#程序，以便更好地比较以上两个算法.公平起见，两个算法都尽可能使用相同的数据结构和子程序，如使用路径集都采用嵌套的泛型集合Dictionary和List来存储，最短路的寻找都采用Dijkstra算法来实现.本文编制的GP算法步长从1递减至0.08，缩小比例为0.95.

表3 三个交通网络的规模Table 3 The size of used traffic networks

图2、图4、图6分别给出了三个网络的旅行时间误差随迭代次数的变化情况.从图中可以发现RCN算法在很少的迭代次数下就能快速收敛，而且精度也非常高.

图3、图5、图7分别给出了三个网络的旅行时间误差随CPU运行时间的变化情况.从图中可以发现Nguyen和淮南市网络下，RCN算法收敛速度非常快，精度也非常高，但在Sioux Falls网络下，RCN算法的优势并不明显.原因是Sioux Falls网络每个起讫点之间均有交通发生和吸引量，这样每次主循环下，需要运算的OD对非常多，大大增加了数据的更新次数，从而增加了运行时间.

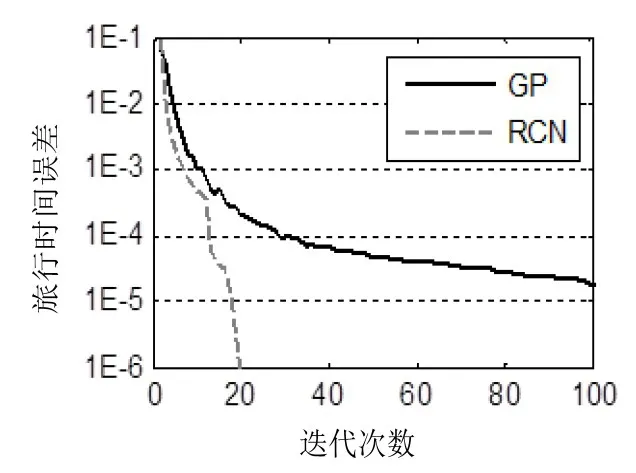
图2 Nguyen旅行时间误差-迭代次数Fig.2 Travel time deviation-iterations of Nguyen

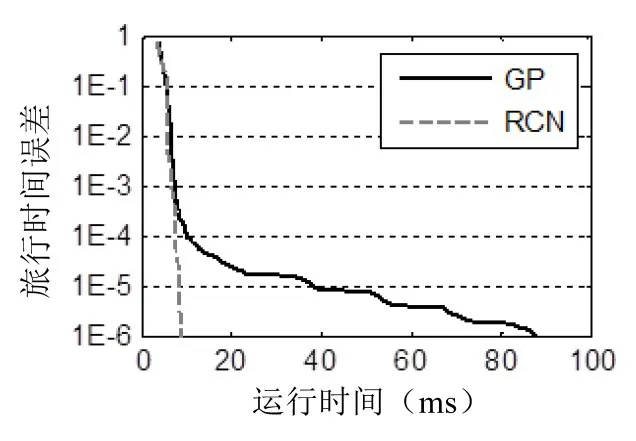
图3 Nguyen旅行时间误差-运行时间Fig.3 Travel time deviation-computing time of Nguyen

图4 Sioux Falls旅行时间误差-迭代次数Fig.4 Travel time deviation-iterations of Sioux Falls

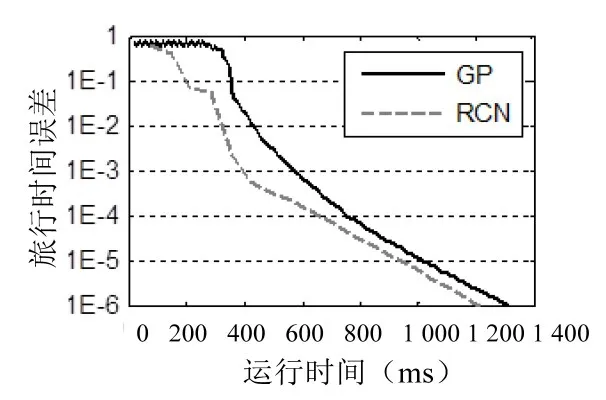
图5 Sioux Falls旅行时间误差-运行时间Fig.5 Travel time deviation-computing time of Sioux Falls

图6 淮南市旅行时间误差-迭代次数Fig.6 Travel time deviation-iterations of HuaiNan

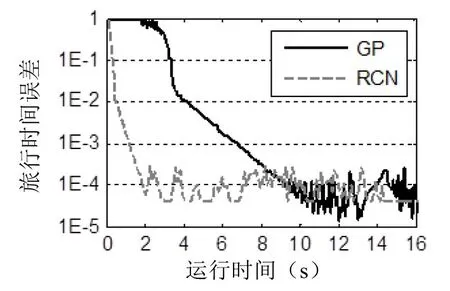
图7 淮南市旅行时间误差-运行时间Fig.7 Travel time deviation-computing time of Sioux Falls

计算实例表明，虽然RCN算法在每次循环过程中不停更新数据，增加了计算时间，但通过使用更为精确的牛顿简化方向和优化步长，使得在很少的迭代步数下，算法就能达到很高的精度，所以不管是在收敛速度还是精度上，RCN算法明显优于GP算法，尤其是在迭代前期，RCN算法成指数速度收敛.

5 研究结论

本文首先运用偏导、积分等数学转换关系得到了以路径费用函数为基础的交通UE模型，该模型的提出为交通流分配算法提供新思路、新方法.进而提出了RCN算法，该算法每次仅对一OD对进行牛顿型流量转移，转移完就更新道路流量，在这基础上，根据“更快速度接近均衡解原则”，计算出牛顿简化方向，并且找到更为精确的优化步长.经过计算实例发现，RCN具有更快的收敛速度和更高的精度，尤其在迭代前期.

经过对RCN算法和GP算法长时间的运算测试，发现RCN算法在前期收敛非常快，但在后期（如淮南市网络精度达到1E-12），RCN并没有什么优势，相反GP这种占内存少、每次循环时间短的算法能稳健到达所需的精度.对RCN算法进行完善、将RCN算法和其他交通分配算法结合使用是进一步的研究工作.

[1] Meyer M D,Miller E J.Urban transportation planning:a decision-oriented approach[M].Second Edition.McGraw-Hill Companies,New York,2001.

[2] Sheffi Y.Urban transportation networks[M].Englewood Cliffs,New Jersey:Prentice-Hall,1985.

[3] LeBlanc L J,Morlok E K,Pierskalla W P.An efficient approach to solving equilibrium traffic assignment problem[J].Transportation Research,1975,9:309-318.

[4] Hearn D W,Lawphongpanich S,Vebtura J A.Restricted simplicial decomposition: Computation and extensions[J]. Mathematical Programming Study, 1987,31:99-118.

[5] Larsson T,Patriksson M.Simplicial decomposition with disaggregated representation for the traffic ssignment problem[J].Transportation Science,1992,26:4-17.

[6] Jayakrishnan R,Tsai W K,Prashker J N,et al.A faster path-based algorithm for traffic assignment[J]. Transportation Research Record,1994,1443:75-83.

[7] Chen A,Jayakrishnan R.A path-based gradient projection algorithm:Effects of equilibration with a restricted path set under two flow update policies[C]. Preprint#981560,in:Proceedings of the Transportation Research Board Annual Meeting,Washington,D.C., 1998.

[8] Cheng L,Xu X D,Qiu S L.Constrained newton methods for transport network equilibrium analysis[J].Tsinghua Science and Technology,2009,14(6):765-775.

[9] Lee D,Nie Y,Chen A.A conjugate gradient projection algorithm for the traffic assignment problem[J]. Mathematical and Computer Modelling,2003,37:863-878.

[10] Florian M,Constantin I,Florian D.A new lood at projected gradient method for equilibrium assignment[J].Transportation Research Record:Journal of the Transportation Research Board,Transportation Research Board of the National Academies,2009, 2090：10-16.

[11] Bar-Gera H.Origin-based algorithms for transportation network modeling[D].Chicago：University of Illinois, 1999.

[12] Bar-Gera H.Origin-based algorithm for the traffic assignment problem[J].Transportation Science,2002, 36:398-417.

[13] Chen A,Lee D,Jayakrishnan R.Computational study of state-of-the-art path-based traffic assignment algorithms[J]. Mathematics and Computers in Simulation,2002,59:509-518.

[14] 孙超，王欣，童蔚苹，等.用户均衡与系统最优原则下交通分配模型的建立与分析[J].中国科技论文，2013，8（11）：1073-1077.[SUN C,WANG X,TONG W P,et al.Establishment and analysis of traffic assignment model under the user equilibrium and system optimization principle[J].China Science Paper,2013,8 (11):1073-1077.]

[15] Nguyen S,Dupuis C.An efficient method for computing traffic equilibria in networks with asymmetric transportation costs[J].Transportation Science,1984, 18:185-202.

[16] LeBlanc L J,Morlok E K,Pierskalla W P.An efficient approach tosolvingequilibrium trafficassignment problem[J].Transportation Research,1975,9:309-318.

[17] 郑中元.城市道路交通网络空间拥堵瓶颈识别[D].南京:东南大学,2009.[ZHENG Z Y.Identification of bottlenecks in urban road network[D].Nanjing: Southeast University,2009.]

Path-based Rapid Convergent Newton Algorithm in Traffic Assignment

CHENG Lin,SUN Chao,SHAO Juan
(School of Transportation,Southeast University,Nanjing 210096,China)

This paper proposes a method for solving the deterministic user equilibrium assignment problem. The UE model based on route cost function is established.Base on this model,path-based rapid convergent Newton(RCN)algorithm is proposed.Each time the traffic flow is diverted for only one OD,and then the flow is updated.We propose the principle of faster speeds approaching equilibrium.Then we simplify the Hessian matrix which can deduce the iterative direction.And through the second-order Taylor expansion,the optimal step size is found.The algorithm is applied to the real traffic assignment problem.Three types (small,medium,large)of traffic networks are tested respectively.Compared to the traditional gradient projection algorithm,path-based rapid convergent Newton algorithm has faster convergence and higher precision,especially in the early iterations.

traffic engineering;path-based Newton algorithm;optimal step size;traffic assignment; simplified direction

2014-04-13

2014-09-14录用日期：2014-10-08

国家自然科学基金（51078085，51178110，51378119）.

程琳（1963-），男，江苏泰州人，教授.

*通讯作者：gist@seu.edu.cn

1009-6744（2014）06-0101-06

U491

A