在资金预算不确定条件下路面维护和修复项目管理决策优化方法

(1.北卡罗来纳大学夏洛特分校土木与环境工程系，夏洛特28223，美国；2.杰克逊州立大学土木与环境工程系，杰克逊39217，美国)

在资金预算不确定条件下路面维护和修复项目管理决策优化方法

(1.北卡罗来纳大学夏洛特分校土木与环境工程系，夏洛特28223，美国；2.杰克逊州立大学土木与环境工程系，杰克逊39217，美国)

一个得到良好开发和维护的路面管理系统（PMS）能够帮助管理者做出在什么时候，对哪些路段采用什么样的路面维护和修复方案的决定，从而实现可用资源的最大化.本文提出一种在资金预算不确定条件下路面维护和修复项目管理决策优化方法(MPMRPBU)，为确保管理者在一个决策规划时段内，从公路网中选择并优化一组路面维护和修复方案，建立随机线性规划模型求解MPMRPBU问题.通过案例分析，比较在确定性优化和随机规划两种不同条件下的优化方案，研究不同经济预算对优化方案的影响.结果表明，采用随机规划方法能产生高质量的MPMRPBU解决方案,该算法可以解决实际问题.

交通工程；路面管理系统；决策；路面维护和修复；优化；随机规划

1 引 言

路面管理系统（PMS）是支持路面维护和修复（M＆R）项目管理决策优化的主要工具.在长达数年的规划期内，决定哪些路段应纳入每年的M＆R项目名单是PMS系统的主要功能之一.路面维护是一种常规的预防性的被动维护方式，通常包括封闭裂缝，修补坑洞，以及其他一些相关的维护方法（焦油碎石封层或喷浆密封）.路面修复是指较大规模的维修行动，旨在加强路面及路基的结构强度，如重铺路面以增加其结构能力，或局部改造路基并重铺路面，以完成道路局部重建.路面维护和路面修复费用都很高，但相比较而言，路面修复更加昂贵.然而政府及有关运输部门（DOT）每年度可用于M＆R的预算通常不能满足所有M＆R的需要.因此研发一个实用程序用于路面管理系统的决策支持，提高DOT对路面维护和修复项目的选择及优化过程的自动化程度，可以很好地节省M＆R成本，提高全系统相关道路的路面表现及服务水平[1].

一个好的PMS决策支持系统可以在两个层面上(网络层面和项目层面上)协助决策者进行路面管理的相关工作[3,4].网络层面通常考虑整个路面网络在整个决策期内M＆R的需求估计及预算计划，项目优先方案和工作时间表的初步制定，可分为规划层和项目选择层[3].规划层要制定预算,以及处理资源在整个网络内的分配；项目选择层涉及优化决定项目的相关次序，以确定哪些项目应在每年的规划时间内实施.项目层面通常涉及工程细节的落实及单个项目的具体实施.近年来，很多研究工作提出了解决PMS网络层面上的决策问题，这其中包括规划层[5-9]和项目选择层的相关决策问题[10,11].

如前所述，一个好的PMS应该能帮助决策者选择路面维护和修复方案，即，使用什么路面维护和修复方案，在什么时间，应用于哪个路段，可以实现整个路面网络上的现有资源最大化.但由于许多不可预知的情况，用于运输管理部门在路面年度维修的预算通常是有变动的.以前的研究很有帮助，但很少有人研究在资金预算不确定条件下的路面维护与修复管理的工程项目问题（MPMRPBU）.在未来的年度资金预算变得更加不确定的条件下，什么是最好的决策，怎样才能促使路面工程师/路面维护经理做出明智的决定，得以最好地利用有限的财政资源.随机规划在交通研究领域有很多应用，包括货运车队管理[12]与汽车共用系统的应用[13].大规模线性规划和多阶段随机规划也在很多文献中提及[14-27].本文为解决在一定规划时间范围内的MPMRPBU问题，建立了MPMRPBU模型并提出一个随机规划的优化方法来解决这一多阶段随机模型.

2 问题描述

众所周知，M＆R的维修可以有任何形式，从最简单最便宜的预防性路面维护到最复杂最昂贵的路面修复.而且，在网络层面上的优化，通常没有必要（有时也不可能）像在项目层面上那样详细.五种不同M＆R维修处理方案如下：

(1)什么都不需要（Needs nothing，NN)；

(2)预防性维护（Preventivemaintenance，PM)；

(3)轻微修复（Light rehabilitation，LRhb)；

(4)中等修复（Mediumrehabilitation，MRhb)；

(5)重度修复（Heavyrehabilitation，HRhb).

在路面维护和修复项目管理决策优化过程中,每个路段实际是一个所谓的管理单元，只能选择上述五种维修方案中的一个对路面进行处理.管理单元是指具有类似结构及路面状况的一段道路，并能够以统一的方式进行养护和维修处理.通过这样对类似路面进行分组，可以减少公路网中路段的数量，从而减少优化模型中决策变量的总数，使问题变得更简单和更容易处理[2,11].

五种M＆R维修处理方案中每个M＆R的效益（或有效性）及成本通常是与道路的路段长度和交通流量密切相关.一般来说，长的路段或拥有较高交通流量的路段会产生更大的M＆R效益和M＆R成本.五种候选M＆R维修处理方案中，每个方案对路面状况的改善和有效寿命的延长，都可以依据每个具体路段来确定.通常情况下，相对于一个预防性的路面维护方案,一个更昂贵的路面修复方案会产生更好的改善效果.图1显示了路面维护和修复处理之前和之后,某个维修处理方案对道路状况的影响，其中eij与lij分别代表该处理方案对第i路段于第 j年执行后路面状况评分的改善及有效寿命的延长.

图1 路面状况评分和M＆R成效Fig.1 Pavement condition score and M&R effectiveness

道路条件的改善可以用两个参数来衡量：道路服务时效的增加和路况评分的提高.道路服务时效的增加可以解释为图1中的两条状况衰减曲线之间道路有效寿命的延长部分（即lij）.路况评分的提高可以解释为图1中两条状况衰减曲线之间路况评分的变化（即eij）.道路状况评分（0-100），取决于道路的病害情况和乘坐品质，由于它是衡量道路条件的一个稳定指数，因此被TxDOT使用.M＆R的维修效益可以用初始增加的路况评分eij乘以延长的有效寿命lij来进行估算.通常，如果路面条件得分低于50,就表明该路面需要某种类型的养护维修措施[1].虽然许多交通部门在网络层次上路面的状况评分通常有一个倾斜（有时甚至是严重倾斜）的分布，而且是分布在一个由100为上限的优秀或良好的路面状况，但为建模简单起见，公路网络的路段状态评分仍然被假定是呈正态分布，即,S～N(μ,σ2),其中S是在公路网的路面状态得分;μ和 σ2分别是正态分布N的均值和方差.一般来讲，从取样观察得到的统计信息可以描述为t分布，而且当自由度超过30时,其t值很接近于正态分布.因此，如果网络中有众多路面单元，这个路面状态得分呈正态分布的假设是令人满意的，尽管在现实条件下，该状态得分实际上可能遵循一个偏态的分布.

为了估计一个道路在未来时间的状况以便制定一个相应的道路状态转换过程公式，我们假设了一个基于恒定衰减率的过渡模型.如图1所示，i路段在j年进行了M&R的维修，并在状态得分上得到了eij的提高.通常可以用历史数据来计算确定一个具体路段i的道路状况恒定衰减率pi.如果初始条件的分数是Si0,并在第 j年路况状态得分增值为eij(其中 j=1,2,…),那么在以后的时间t (t＞j)里路面状况Sit可以用式（1）来计算.

显然，路面单元可能表现得非常不同,因此恒定的衰减率模型是远远不能够用来精确描述路况的复杂转换过程.此外，经过预防性养护和大修修复措施的路面表现可能会很不同，因此针对每个M＆R维修后的路面来确定不同的衰减率是更合适的.同时，更精确的性能曲线，以及每一个路面的衰减特性都可以从历史或其他相关数据来分析并获得[2].换句话说，针对每个路段,一个类似于式（1）的道路状况预测模型是可以被建立和校准的，并可在本优化模型中采用.

可以用TxDOT PMIS数据库中各种与路面相关的历史数据来标定前面讨论过的参数.本文假定对于五种M＆R维修方案中的每个路面初始路况得分、衰减速度、M＆R的单位成本，以及M＆R对路况改善的成效跟有效使用寿命的延长数据都可以从网络中的相应路段的路面管理信息系统数据库检索或计算到.为了使模型更简单，本文不考虑现金折现率，我们对所有的成本进行评估，并用目前的美元价值.我们也假定,在五年规划期内,各公路管理单元每年至多只能有一个M＆R维修的措施方案，而且在五年规划期内总维修数可能是有上限的.最后，我们假设规划时间长度为五年，因为在这样短的时间内一个路面单元通常只会需要很少的M＆R维修处理.在网络层面上的路面养护和修复规划中，五到十年是一种比较流行的分析周期[9,11].

3 建立模型

根据前面讨论,我们制定了一个ILP优化模型,表述如下.

设置/指数：

i——路段（路面单元）；

j——年；

k——养护维修方案.

参数/数据:

n——网络中的路段总数；

m——规划周期内的总年数；

r——候选M＆R维修方案的总数；

ai——路段i的每车道日均车流量；

di——路段i的公里长度；

eik——维修方案k导致路段i的路况加分；

lik——维修方案k导致路段i以年为单位的有效寿命；

cik——维修方案k导致路段i的每车道公里单位成本（以千美元为单位）；

bj——第j年的总提供预算（以千美元为单位）；

pi——路段i状况的衰减率；

g1——道路用户对所有路段中每个路段道路状况得分的最低要求；

g2——客观上所有路段中每个路段可能的最大道路状况评分值；

g3——在计划周期内的每个路段所允许的最多维修数量；

g4——对网络层次下,决策者对路况分数平均统计值的最低要求.

随机变量:

决策变量:

xijk——在第 j年路段i维修方案k的决策变量,如果选定则取值为1,否则为0；

Sij——在第 j年路段i的基于初始条件得分为Si0的道路状况的衍生决策变量.目标函数:

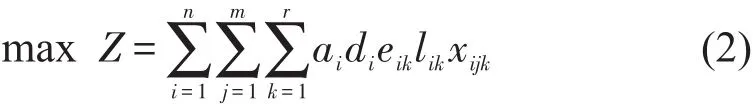
约束条件

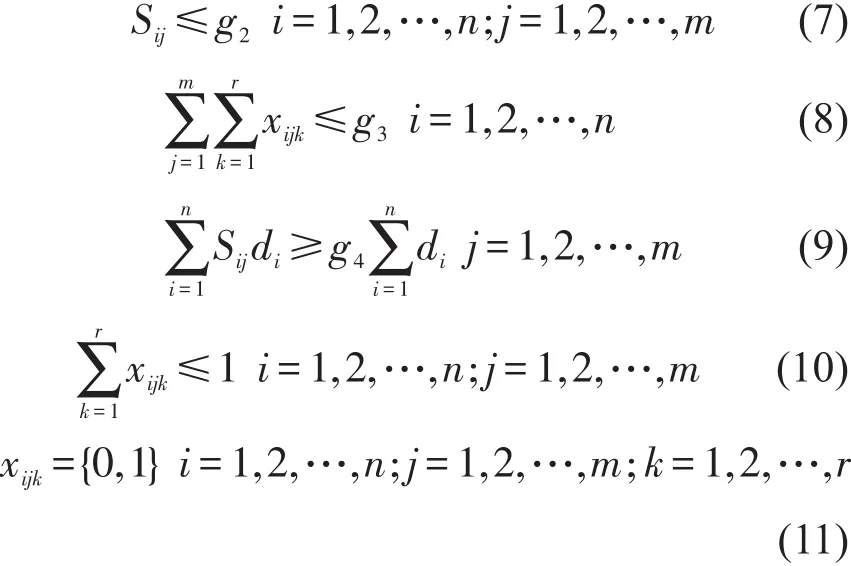
式（2）中可以看出,我们的目标是在规划范围内，尽可能最大化整个网络的M＆R成效（即加权条件下的得分点）.式（3）和式（4）分别指在第一年，以及所有未来几年的预算约束.

4 情景树的生成

图2给出了一个基于多阶段随机规划模型的完整场景树（也即情景树）.在图2中,树中的节点代表某一特定时期t的状态.在节点做出决策，弧代表不确定变量的实现.在下面（后面）的情景树里做出的决定依赖于在前面父节点已经作出的决定及后面的子节点的某种不确定性，比如图2中的L（低），M（中）和H（高）年度预算方案.需要注意的是，场景的生成是基于假定的离散分布，而且决策者可以指定某种概率分布函数，这样问题的统计特性就可以明确加以利用.一个完整的情景树包含在每个时间段（或每阶段）的不确定变量的实现.实践中，只有在第一阶段的顶部节点的解将被用于管理决策.在第二阶段及其后作出的决定只是为了找到第一阶段决策正确的激励机制[27].

在第一个时间段的开头，决策的做出是基于当前的信息（和随机未来的实现）.在第一个时间段的结尾，这个决定的后果会显现.鉴于这一后果和下一阶段的新信息，一个新的决定会在第二时间段的开始时做出.基于第二时间的结果和第三时间段给出的新信息,决定会再次做出.整个决策过程在原则上会一直持续下去.需要注意的是，一旦每个情景树实现生成了随机变量，我们可以使用精确的优化方法(比如L形的方法[20])去求解.事实上，在第一阶段的管理决策就是这样得到的.

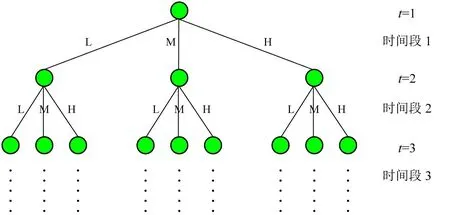
图2 基于多阶段随机规划模型的场景树Fig.2 Scenario tree for multi-stage stochastic programming models

5 数值结果

5.1 例示网络和数据准备

为了测试建立的模型,本研究选择设计了一个由5个时间段（以年为单位）和10个路段为代表的实验网络来研究MPMRPBU问题，并且测试了使用所开发的随机规划方法来解决MPMRPBU问题的解的质量和效率.输入数据由所有十个路段的 pi,Si0,ai,和di，以及所有10个路段和5种候选M＆R维修方案的cik,eik,和lik组成.这些输入数据是集合TxDOT的相关研究报告中的信息编制而成.第一年的M＆R预算b1在运行该优化模型的时候已知，并假定为 $364 000.然而在该模型中，在所有未来的四年里，预算数据bj(j=2,3,4,5)都是随机的，但假定服从一个由三种情况所组成的离散分布(平均预算为每年$364 000).低（LOW）预算方案为每年bj= $300 000 (j=2,3,4,5)的 概 率 是 0.4,中（MED）预 算 方 案 为 每 年 bj= $360 000 (j=2,3,4,5)的概率是0.4,高（HIGH）预算方案为每年bj=$500 000(j=2,3,4,5)的概率是0.2.表1显示了一个典型的路面管理路段的数据输入.

需要注意的是，M＆R维修方案单位成本为千美元每车道公里.g1到g4的值也需要决定.依据TxDOT的做法,g1=50,g2=100.g3的值规定了在5年的规划周期内所允许的每个路段所能维修的总次数，即不应该大于5(在最坏情况下，在设计期间内，一个路段每年都要维修).g4值由网络中假定呈正态分布的状态分数来确定,即S～N(μ,σ2).对于参数μ和σ,在整个网络中路段条件得分比Sα更好的概率为α，g4值可以由 μ=g4=Sα+(Zα)(σ)计算.例如,德州交通专员约翰逊关于可允许的最低网络路面状况的说法“在网络中90%的路段应该有70或更高的状况得分”可被解释为g4=70+(1.29)×(10)=83(如果σ被假定为10).σ值（路面状况指数标准差）可以用历史数据来获得. α和Sα值可以作为用户要求的网络中未来状况分数平均值的最低要求来输入[1].另外，优化模型是用基于SAS的宏开发的OPTMODEL来解决的[28].

表1 路段i的数据输入Table 1 Data input for road section i

5.2 计算结果

5.2.1 确定性的优化方法

在本节中,确定性的优化方法(DOA)也指平均预算解决方法.忽略可能会引起计算不便的某种不确定性，通过使用这些随机变量的期望值，做出启发式的决策.路面工程师/维修经理可能使用年度平均预算来做决策，然后通过优化这个“平均预算”方案来执行最佳解决方案.利用这种确定性的优化方法得到的数值结果说明如下.

（1）年度预算影响.

本节进行基于年度预算的敏感性分析.图3显示了预算对目标值Z的影响.在图3中可以看到，随着年度预算从$200 000往上增加,M＆R效益目标函数值Z也会在非常大的预算范围内显著增加，但这之后随着预算的增加,这种改进变得并不明显.这一结果表明，增加年度预算是一种可以增加总M＆R效益的有效方法.

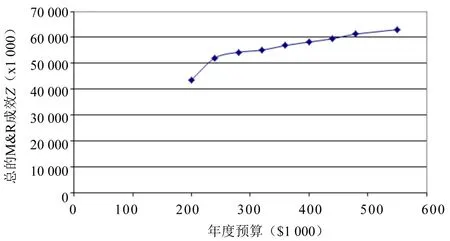
图3 目标函数值Z与年度预算Fig.3 Objective Z versus annual budget

（2）基于确定性优化方法的解决方案.

表2列出了在两个不同预算条件下决策变量的解.该决策变量的解显示了当预算变得更严格时，路面维护和修复最优解通常会选用成本较低的M＆R维修方案.然而在这种情况下，为了使路面部分保持在某种可接受的情况下，具有高衰减率的路面可能需要更频繁地维护或修复.这种趋势实际上是反映路面维护和修复战略的差异.在路面维护和修复问题的研究上有两个相反的策略可以被利用以解决路面问题，即“掩盖它”或“修复它”.在现实中,如果在解决道路相关结构问题时只采取预防性维护或小修复,那么结构性问题只是在短时间内被掩盖起来，相同的问题在不久的将来肯定会很快重现.表2中的优化结果表明，如果M＆R预算较高，具有更高成本的修复方案（通常是预防性的维护和修复的正常组合）会比成本较低的修复方案更有效，因此，这些方案会被推荐在M＆R的优化项目列表中.而对于较低的M＆R预算来说，只有预防性维护或小修复会被选作可行的解决方案.虽然可行的解决方案仍然是网络的最优解，但从长远考虑，这些修复不一定是最节省成本的方案.

5.2.2 随机规划（优化）方法

如前面所提到的,随机优化（SP）是一个建模框架，通常用来处理一些问题数据中的不确定性(预算的不确定性).这种不确定性表现为三种预算情形（高、中、低预算），解决MPMRPBU问题是需要考虑这种不确定性的，而不是等到不确定性出现后再寻找一种方法解决它.由于未来的预算是未知的，但必须在当期（即第一阶段）做出决定，因此对所有场景来说，所有第一阶段的优化决策值必须是一样的.利用开发的SAS宏代码，SP的解是在三个不确定预算水平的情况下获得的，考虑合并所有可能出现的情况，表3中所述的结果为SP=55 133 760.该值意味着，如果执行SP解的决定，可以期望总M＆R效用值为$557 337 60.

路面维护工程师或维修经理可能会计算5.2.1中（2）的三个不确定水平场景的平均预算（即，364 000美元/年），然后只优化“平均预算”的情况，取得并执行最佳解决方案的决定.如果用预算平均值替换随机预算，问题就能得到解决，表3所示的结果是EB=57 312 000，这意味着总M＆R的效益将会是57 312 000.如果执行SP的解，SP的解决方案仅是55 733 760.这是预期的，因为该问题已经从一个随机规划问题变为确定性优化问题.当预算是确定的，而不是随机的，我们具有完善的预算信息，作为结果，相对于随机规划方法SP=55 733 760的目标函数值，我们当然可以得到一个更好的解决方案.另外，平均值问题的目标函数值大于随机问题的目标函数值，这正符合Jensen不等式的原则[20,21].

表3 试验研究数值结果Table 3 Pilot study numerical results

5.2.3 随机解决方案的价值

SP解决方案的成本和使用“平均预算”解决方案的预期总成本之间的差额(对平均预算的解在随机环境下进行评价)可以定义为随机解决方案的价值（VSS）.

如果平均预算问题的解在随机预算环境下评估，随机问题的目标函数变为：EEB=54 769 926，表示这是一个比SP的解（SP=55 733 760）实际上要差的解决办法.VSS可以计算为VSS=SPEEB=963 834，这可以解释为通过忽略预算的不确定性的M＆R决定的成本.虽然这个数值并不是很大，但对于一个大型网络下长时间范围内的总价值来说，却非常显著.因此，随机优化解决方案比平均预算的解决方案要更有效.

6 研究结论

本文针对一个不确定性预算条件下路面管理维护和修复项目（MPMRPBU）的决策问题，制定了一个随机线性规划模型，求解了MPMRPBU.计算结果是基于一个案例研究得到的.本文比较和讨论了在确定性优化和随机规划两种不同条件下的优化方案.研究了预算对优化解决方案的影响，表明“总的M＆R效益的最大化”目标是与相关预算增加成正比.通过对决策变量的分析表明，增加预算可能会导致M＆R项目的清单中包含更贵的维修方案.计算结果也表明采用随机规划方法能产生高质量的MPMRPBU的解决方案,因此该算法可以用于实际中.

然而，应该指出的是，由于计算时间和SAS/ OPTMODEL求解能力的限制，使用随机规划方法来求解MPMRPBU的执行时间可能会很长，而且，算法收敛可能也是一个比较现实的问题.在这种情况下，接受足够好的可行解与适当的容忍收敛差距可能是必须要选择的方法.作为未来研究的一个重要组成部分，以及CPLEX本身对大规模优化问题的求解速度和能力，可以值得认真尝试.然而，采用随机规划方法来解决MPMRPBU的问题确实显示出高潜力，随着研究日趋成熟，将会大有希望.

[1] Wang F,Zhang Z,Machemehl R B.Decision-making problem formanagingpavementmaintenanceand rehabilitation projects[R]. Transportation Research Record 1853,TRB,NationalResearch Council, Washington D.C.,2003.

[2] Stampley B E,Miller B,Smith R E,et al.Pavement management information system concepts,equations, and analysis models[R].TTI Research Report 1989-1. Texas A&M University,Texas.1995.

[3] Haas R,Hudson W R,Zaniewski J.Modern pavement management[M].Krieger Publishing Company,Malabar, Florida,1994.

[4] Zhang Z.A GIS based and multimedia integrated infrastructure management system[D].Texas:The University of Texas at Austin,1996.

[5] Grivas D A,Ravirala V,Schultz B C.State increment optimization methodology for network-level pavement management[R].Transportation Research Record 1397, TRB,National Research Council,Washington D.C., 1993.

[6] Chen X,Hudson S,Pajoh M，et al.Development of new network optimization model for oklahoma department of transportation[R]. Transportation Research Record 1524,TRB,National Research Council,Washington D. C.,1997.

[7] Liu F,Wang K C P.Pavement performance-oriented network optimization system[R]. Transportation Research Record 1524,TRB,NationalResearch Council,Washington D.C.,1997:86-93.

[8] Mbwana J R,Turnquist M A.Optimization modeling forenhanced network-levelpavementmanagement systems[R].Transportation Research Record 1524, TRB,National Research Council,Washington D.C., 1997.

[9] Abaza K A,Ashur S A.Optimum decision policy for management of pavement maintenance and rehabilitation[R].Transportation Research Record 1655, TRB,National Research Council,Washington D.C., 1999.

[10] Sharaf E A.Ranking vs.simple optimization in setting pavement maintenance priorities:A case study from egypt[R].Transportation Research Record 1397,TRB, National Research Council,Washington D.C.,1993.

[11] Zambrano F,Scullion T,Smith R E.Comparing ranking and optimization procedures for the texas pavement managementinformation system[R].TTIResearch Report 1989-2F.Texas A&M University,Texas.1995.

[12] Fan W,Machemehl R B.A multi-stage monte carlo sampling based stochastic programming model for the dynamic vehicle allocation problem[J].Journalof Advances in Transportation Studies,2007,12:27-44.

[13] Fan W,Machemehl R B,Lownes N E.Carsharing:a dynamic vehicle allocation decision making problem[R]. Transportation Research Record 2063,TRB,National Research Council,Washington D.C.,2008.

[14] Dantzig G.Linear programming under uncertainty[J]. Management Science,1955,1:197-206.

[15] Dantzig G,Wolfe P.Decomposition principle for linear programs[J].Operations Research,1960,8:101-111.

[16] Ziemba W.Computationalalgorithms forconvex stochastic programs with simple recourse[J].Operations Research,1970,18:414-431.

[17] WollmerR.Twostatelinearprogrammingunder uncertainty with 0-1 integer first stage variables[J]. Mathematical Programming,1980,19:279-288.

[18] WetsR.Solving stochastic programswith simple recourse[J].Stochastics,1983,10:219-242.

[19] Birge J.Decomposition and partitioning techniques for multistage stochastic linear programs[J].Operations Research,1985,33:989-1007.

[20] Birge J R,Louveaux.Introduction to stochastic programming[M]. New York: Springer Series in Operations Research,1997.

[21] Morton D P.Stochastic optimization class notes[D]. Texas:The University of Texas at Austin,2002.

[22] Wallace S.Solving stochastic programs with network recourse[J].Networks,1986,16:295-317.

[23] Beale E,Dantzig G B,Watson R D.A first order approach to a class of multi-time period stochastic programming problems[J].Mathematical Program Study, 1986,27:103-177.

[24] Zenios S A.Dynamic models for fixed-income portfolio management under uncertainty[J].Journal of Economic Dynamics and Control,1998,22:1517-1541.

[25] Kouwenberg R.Scenario generation and stochastic programming models for asset liability management[J]. European Journal of Operational Research,2001,134: 279-292.

[26] Hoyland K,Wallace S W.Generating scenario trees for multistage decision problems[J].Management Science, 2001,47(2):295-307.

[27] Fleten S E,Hoyland K,Wallace S W.The performance of stochastic dynamic and fixed mix portfolio models[J]. European Journal of Operational Research,2002,140: 37-49.

[28] SAS∕OR®9.22 User’s guide mathematical programming [OL],SAS Institute Inc.,Cary,NC,USA.[2012-6-4] http:∕support.sas.com∕documentation∕cdl∕en∕ormpug∕63352∕PDF∕default∕ormpug.pdf,2010.

FAN(David)Wei*1,WANG Feng2

Managing Pavement Maintenance and Rehabilitation Projects under Budget Uncertainties

FAN(David)Wei1,WANG Feng2
(1.Department of Civil and Environmental Engineering,University of North Carolina at Charlotte,Charlotte 28223,USA；2.Department of Civil and Environmental Engineering,Jackson State University,Jackson 39217,USA)

A well-developed and maintained pavement management system(PMS)empowers a decision maker to select the best maintenance program,i.e.,which maintenance treatment to use and where and when to apply it,so that a maximum utilization of available resources can be achieved.This paper addresses a decision making problem for managing pavement maintenance and rehabilitation projects under budget uncertainty(MPMRPBU).A stochastic linear programming model is formulated and solved for the MPMRPBU so that a set of candidate projects can be optimally selected from the highway network over a planning horizon.Numerical results are discussed based upon a pilot case study.Different optimization solutions based on deterministic optimization and stochastic programming approaches are discussed and compared.The effect of the budget constraint on the optimized solutions is investigated.The computational result indicates a high quality MPMRPBU solution using stochastic programming approach,suggesting that there is a potential that the algorithm can be used for real world applications.

traffic engineering;pavement management systems;decision making;pavement maintenance and rehabilitation;optimization;stochastic programming

2012-11-12

2013-10-24录用日期：2014-04-11

作者信息：FAN(David)Wei（1974-），男，副教授，博士. *

wfan7@uncc.edu

1009-6744（2014）06-0092-09

U491

A